1.1.1 空间向量及其线性运算(分层练习)(Word版含解析)
文档属性
| 名称 | 1.1.1 空间向量及其线性运算(分层练习)(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 203.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 00:00:00 | ||
图片预览

文档简介
1.1.1 空间向量及其线性运算
基 础 练
巩固新知 夯实基础
1.判断下列各命题的真假:
①向量a与b平行,则a与b的方向相同或相反;
②两个有共同起点而且相等的向量,其终点必相同;
③两个有公共终点的向量,一定是共线向量;
④有向线段就是向量,向量就是有向线段.
其中假命题的个数为( )
A.2 B.3
C.4 D.5
2.已知空间向量、、、,则下列结论正确的是( )
A.=+ B.-+=
C.=++ D.=-
3.在正方体ABCD-A1B1C1D1中,向量表达式-+化简后的结果是( )
A. B.
C. D.
4.已知正方形ABCD的边长为1,设=a,=b,=c,则|a+b+c|等于( )
A.0 B.3 C.2+ D.2
5.在平行六面体ABCD-A1B1C1D1中,向量,,是( )
A.有相同起点的向量 B.等长向量
C.共面向量 D.不共面向量
6.已知向量a,b,且=a+2b,=-5a+6b,=7a-2b,则一定共线的三点是( )
A.A,B,D B.A,B,C
C.B,C,D D.A,C,D
7.已知P为空间中任意一点,A,B,C,D四点满足任意三点均不共线,但四点共面,且=-x+ ,则实数x的值为( )
A. B.- C. D.-
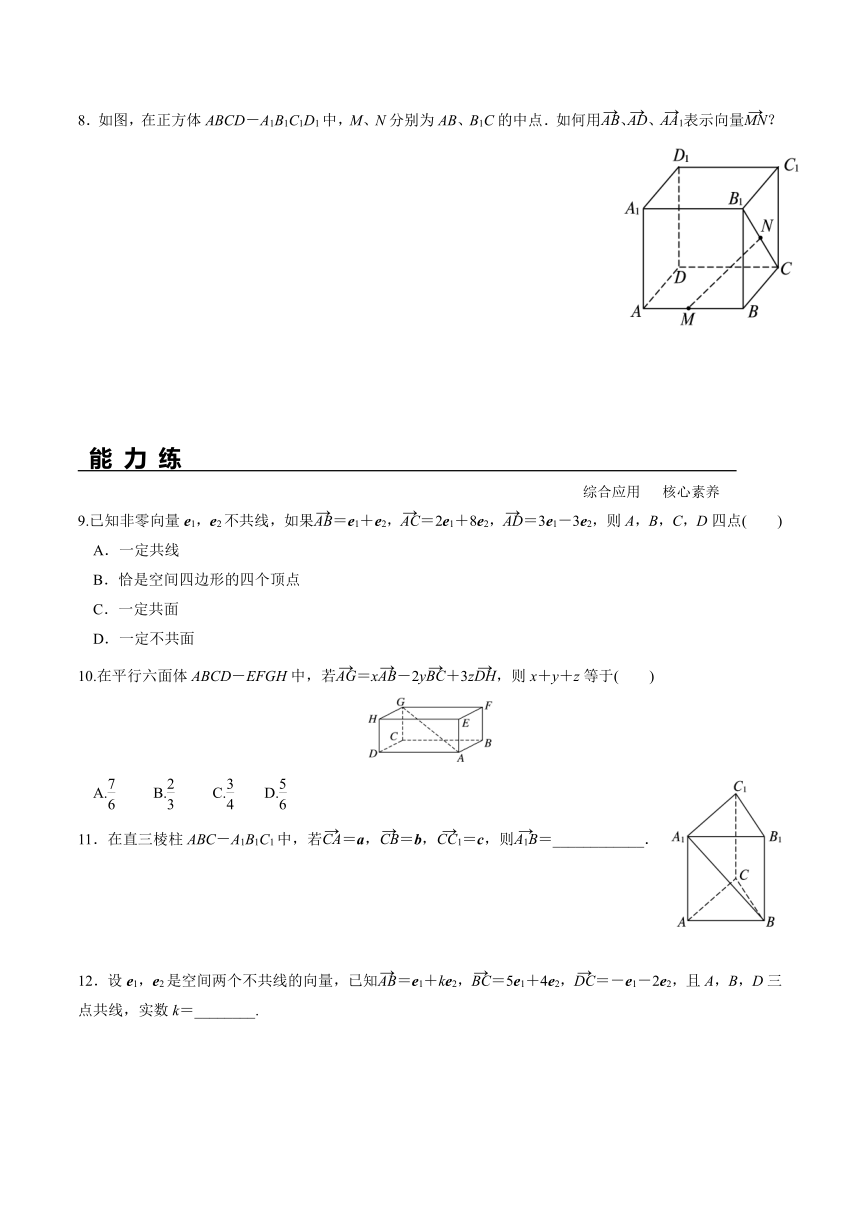
8.如图,在正方体ABCD-A1B1C1D1中,M、N分别为AB、B1C的中点.如何用、、表示向量?
能 力 练
综合应用 核心素养
9.已知非零向量e1,e2不共线,如果=e1+e2,=2e1+8e2,=3e1-3e2,则A,B,C,D四点( )
A.一定共线
B.恰是空间四边形的四个顶点
C.一定共面
D.一定不共面
10.在平行六面体ABCD-EFGH中,若=x-2y+3z,则x+y+z等于( )
A. B. C. D.
11.在直三棱柱ABC-A1B1C1中,若=a,=b,=c,则=____________.
12.设e1,e2是空间两个不共线的向量,已知=e1+ke2,=5e1+4e2,=-e1-2e2,且A,B,D三点共线,实数k=________.
13.在长方体ABCD-A1B1C1D1中,化简-+-+-.
14 . 如图,设O为 ABCD所在平面外任意一点,E为OC的中点,若=+x+y,求x,y的值.
15.如图所示,已知空间四边形ABCD,连接AC,BD,E,F,G分别是BC,CD,DB的中点,请化简
(1)++;
(2)++,并标出化简结果的向量.
16.已知点G是△ABC的重心,O是空间任意一点,若++=λ,求λ的值.
【参考答案】
1. B 解析①假命题,若a与b中有一个为零向量时,其方向是不确定的;②真命题;③假命题,终点相同并不能说明这两个向量的方向相同或相反;④假命题,向量可用有向线段来表示,但并不是有向线段.
2.B【解析】-+=++=+=.
3. A解析 如图所示,因为=,-=-=,+=,
∴-+=.
4.D【解析】利用向量加法的平行四边形法则结合正方形性质求解,|a+b+c|=2||=2.
5. C 解析 因为-=,且=,
所以-=,即=+.
又与不共线,所以,,三向量共面.
6. A 解析 因为=++=3a+6b=3(a+2b)=3,故∥,又与有公共点A,
所以A,B,D三点共线.
7. A 解析 =-x+=-x+(-)=-x-.
又∵P是空间任意一点,A,B,C,D四点满足任意三点均不共线,但四点共面,∴-x-=1,解得x=.
8. 解 =++=++(+)=++(-+)=++.
9. C 解析 因为非零向量e1,e2不共线,=e1+e2,=2e1+8e2,=3e1-3e2,所以5-=5e1+5e2-3e1+3e2=2e1+8e2=,所以=5-.由向量共面的充要条件可知,A,B,C,D四点共面.
10. D 解析 由于=++=++,对照已知式子可得x=1,-2y=1,3z=1,故x=1,y=-,z=,从而x+y+z=.
11. -a+b-c解析 =+=+(-)=-+-=-c+b-a.
12. 1 解析 ∵=++=7e1+(k+6)e2,且与共线,故=x,
即7e1+(k+6)e2=xe1+xke2,故(7-x)e1+(k+6-xk)e2=0,
又∵e1,e2不共线,∴解得故k的值为1.
13. 解 -+-+-=(-)+(-) +(-)=++=+=.
14. 解 因为=++=-+--=-+=-+(+)
=-+(+)=-++(-)=-++,
所以x=,y=-.
解 (1)++=+=.
(2)∵E,F,G分别为BC,CD,DB的中点.
∴=,=.
∴++=++=.
故所求向量,如图所示.
16.解:连接CG并延长交AB于D,
则D为AB中点,且CG=2GD,
所以++=+++++
=3+++=3+2+=3-+=3.
所以λ=3.
基 础 练
巩固新知 夯实基础
1.判断下列各命题的真假:
①向量a与b平行,则a与b的方向相同或相反;
②两个有共同起点而且相等的向量,其终点必相同;
③两个有公共终点的向量,一定是共线向量;
④有向线段就是向量,向量就是有向线段.
其中假命题的个数为( )
A.2 B.3
C.4 D.5
2.已知空间向量、、、,则下列结论正确的是( )
A.=+ B.-+=
C.=++ D.=-
3.在正方体ABCD-A1B1C1D1中,向量表达式-+化简后的结果是( )
A. B.
C. D.
4.已知正方形ABCD的边长为1,设=a,=b,=c,则|a+b+c|等于( )
A.0 B.3 C.2+ D.2
5.在平行六面体ABCD-A1B1C1D1中,向量,,是( )
A.有相同起点的向量 B.等长向量
C.共面向量 D.不共面向量
6.已知向量a,b,且=a+2b,=-5a+6b,=7a-2b,则一定共线的三点是( )
A.A,B,D B.A,B,C
C.B,C,D D.A,C,D
7.已知P为空间中任意一点,A,B,C,D四点满足任意三点均不共线,但四点共面,且=-x+ ,则实数x的值为( )
A. B.- C. D.-
8.如图,在正方体ABCD-A1B1C1D1中,M、N分别为AB、B1C的中点.如何用、、表示向量?
能 力 练
综合应用 核心素养
9.已知非零向量e1,e2不共线,如果=e1+e2,=2e1+8e2,=3e1-3e2,则A,B,C,D四点( )
A.一定共线
B.恰是空间四边形的四个顶点
C.一定共面
D.一定不共面
10.在平行六面体ABCD-EFGH中,若=x-2y+3z,则x+y+z等于( )
A. B. C. D.
11.在直三棱柱ABC-A1B1C1中,若=a,=b,=c,则=____________.
12.设e1,e2是空间两个不共线的向量,已知=e1+ke2,=5e1+4e2,=-e1-2e2,且A,B,D三点共线,实数k=________.
13.在长方体ABCD-A1B1C1D1中,化简-+-+-.
14 . 如图,设O为 ABCD所在平面外任意一点,E为OC的中点,若=+x+y,求x,y的值.
15.如图所示,已知空间四边形ABCD,连接AC,BD,E,F,G分别是BC,CD,DB的中点,请化简
(1)++;
(2)++,并标出化简结果的向量.
16.已知点G是△ABC的重心,O是空间任意一点,若++=λ,求λ的值.
【参考答案】
1. B 解析①假命题,若a与b中有一个为零向量时,其方向是不确定的;②真命题;③假命题,终点相同并不能说明这两个向量的方向相同或相反;④假命题,向量可用有向线段来表示,但并不是有向线段.
2.B【解析】-+=++=+=.
3. A解析 如图所示,因为=,-=-=,+=,
∴-+=.
4.D【解析】利用向量加法的平行四边形法则结合正方形性质求解,|a+b+c|=2||=2.
5. C 解析 因为-=,且=,
所以-=,即=+.
又与不共线,所以,,三向量共面.
6. A 解析 因为=++=3a+6b=3(a+2b)=3,故∥,又与有公共点A,
所以A,B,D三点共线.
7. A 解析 =-x+=-x+(-)=-x-.
又∵P是空间任意一点,A,B,C,D四点满足任意三点均不共线,但四点共面,∴-x-=1,解得x=.
8. 解 =++=++(+)=++(-+)=++.
9. C 解析 因为非零向量e1,e2不共线,=e1+e2,=2e1+8e2,=3e1-3e2,所以5-=5e1+5e2-3e1+3e2=2e1+8e2=,所以=5-.由向量共面的充要条件可知,A,B,C,D四点共面.
10. D 解析 由于=++=++,对照已知式子可得x=1,-2y=1,3z=1,故x=1,y=-,z=,从而x+y+z=.
11. -a+b-c解析 =+=+(-)=-+-=-c+b-a.
12. 1 解析 ∵=++=7e1+(k+6)e2,且与共线,故=x,
即7e1+(k+6)e2=xe1+xke2,故(7-x)e1+(k+6-xk)e2=0,
又∵e1,e2不共线,∴解得故k的值为1.
13. 解 -+-+-=(-)+(-) +(-)=++=+=.
14. 解 因为=++=-+--=-+=-+(+)
=-+(+)=-++(-)=-++,
所以x=,y=-.
解 (1)++=+=.
(2)∵E,F,G分别为BC,CD,DB的中点.
∴=,=.
∴++=++=.
故所求向量,如图所示.
16.解:连接CG并延长交AB于D,
则D为AB中点,且CG=2GD,
所以++=+++++
=3+++=3+2+=3-+=3.
所以λ=3.
