新课标苏教版六上3.9《树叶中的比》课件(33张PPT)
文档属性
| 名称 | 新课标苏教版六上3.9《树叶中的比》课件(33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 09:10:48 | ||
图片预览









文档简介
(共33张PPT)
树叶中的比
苏教版六年级上册
教学目标
1.学习目标描述:通过观察、测量、计算、比较、分析等活动,探索并发现一些常见树叶的长与宽的比,感受到树叶的形状与它的长与宽的比之间的关系,进一步积累数学活动经验,发展数据分析观念,增强探索意识和创新意识。
2.学习内容分析:这部分内容是在学生掌握了比的相关知识,特别是学习了如何求比值之后安排的一个实践活动——测量树叶中的比。通过测量、比较同一种树叶的长和宽的比值, 发现树叶中隐藏的秘密。比如同一种树叶,长和宽的比值都比较接近;比值接近的不同树
教学目标
叶, 形状也相似;树叶长与宽的比值越大,树叶就越狭长等等。让学生在动手操作的过程中进一步体验比在现实生活中的应用,加强学生对比的认识。
3.学科核心素养分析:使学生能积极愉悦地参与探究活动,并在探索、发现树叶中有关规律的活动中,初步感受自然现象中蕴含的简单规律,培养用数学眼光观察生活的意识和能力, 感受数学活动的意义及价值,强学习数学、应用数学的兴趣。
新知导入
1.填一填。
长方形长与宽的比是( ),比值是( )。
长方形宽与长的比是( ),比值是( )。
16厘米
6厘米
8:3
8
3
3:8
3
8
新知导入
怎样求出两个数的比值?
用比的前项除以比的后项所得的商就是比值,比值可以是分数,也可以是小数,还可以是整数。
新知导入
2.求比值。
0.08:0.5 1.2米:60厘米 :
1
6
1
10
=0.08÷0.5
=0.16
=120厘米:60厘米
=120÷60
=2
= ÷
1
6
1
10
= ×
1
6
10
=
5
3
新知导入
猜
一
猜
春来穿新衣,
秋来换新装。
夏至刷绿漆,
冬至落满地。
(打一植物构造)
新知导入
树叶对于我们来说非常熟悉,在我们生活中随处可见。树叶可以为我们提供氧气,从而达到净化空气的效果,也给我们带来了美的享受。
新知讲解
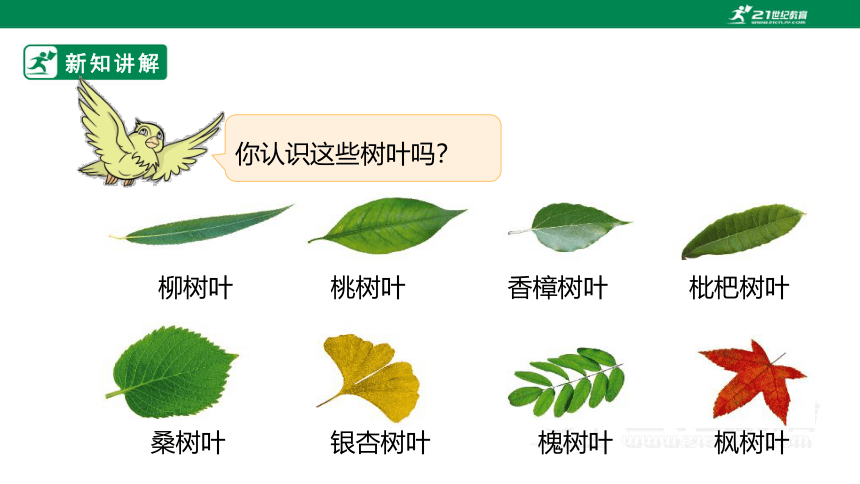
你认识这些树叶吗?
柳树叶
桃树叶
香樟树叶
枇杷树叶
桑树叶
银杏树叶
槐树叶
枫树叶
新知讲解
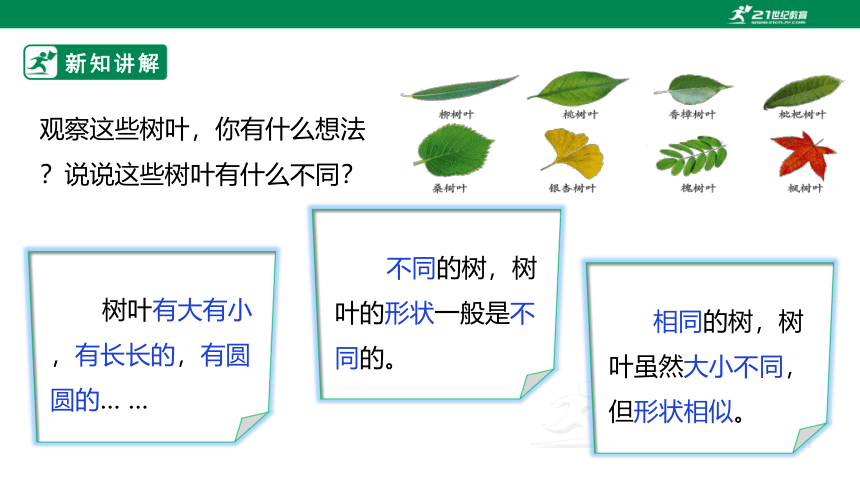
观察这些树叶,你有什么想法?说说这些树叶有什么不同?
树叶有大有小,有长长的,有圆圆的… …
不同的树,树叶的形状一般是不同的。
相同的树,树叶虽然大小不同,但形状相似。
新知讲解
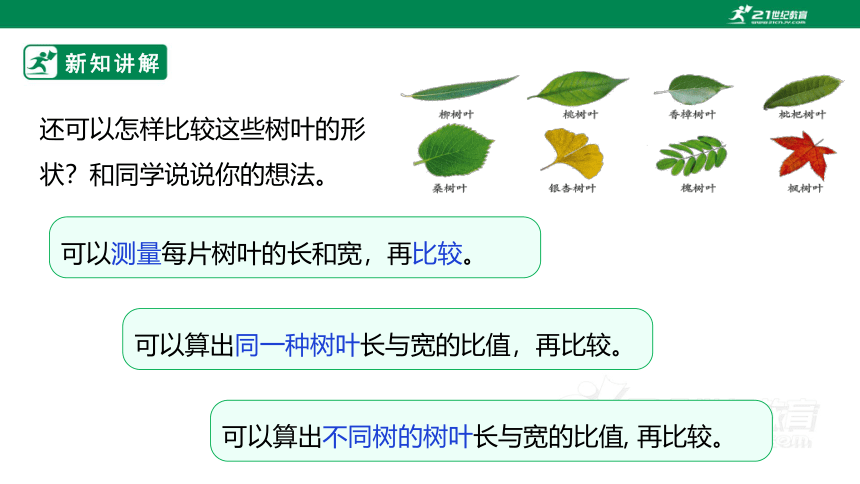
还可以怎样比较这些树叶的形状?和同学说说你的想法。
可以测量每片树叶的长和宽,再比较。
可以算出同一种树叶长与宽的比值,再比较。
可以算出不同树的树叶长与宽的比值, 再比较。
新知讲解
你知道吗?
测量、计算和比较都是我们探究数学问题的常用方法。
新知讲解
你知道怎么测量树叶的长和宽吗?指一指下面两片树叶的长和宽该如何测量。
树叶的长一般是指沿主叶脉方向量出的最长距离的长度(不含叶柄),宽一般是指树叶中沿与主叶脉垂直方向量出的最宽处。
新知讲解
长
宽
长
宽
选择一片喜欢的树叶, 指一指它的长和宽。
新知讲解
活动要求:
(1)每组测量同一种树的树叶(10片), 组长明确分工。
(2)量出每一片树叶的长和宽,算出长与宽的比值(得数保留一位小数),填入右表。
新知讲解
( )树叶的长和宽及比值
香樟树
编号 长/mm 宽/mm 比值 编号 长/mm 宽/mm 比值
1 370 150 2.5 6 360 152 2.4
2 550 220 2.5 7 180 74 2.4
3 960 420 2.3 8 251 105 2.4
4 136 58 2.3 9 78 29 2.3
5 121 50 2.4 10 222 100 2.2
新知讲解
( )树叶的长和宽及比值
柳树
编号 长/mm 宽/mm 比值 编号 长/mm 宽/mm 比值
1 543 52 10.3 6 621 61 10.3
2 277 29 10.2 7 704 68 10.4
3 102 10 10.2 8 230 22 10.3
4 410 42 10 9 147 14 10.5
5 56 6 10.2 10 201 20 10.2
新知讲解
分小组计算各自测量的10片树叶长与宽比值的平均数(得数保留一位小数)。
柳树叶
10.3
柳树叶
10.2
榆树叶
2.5
榆树叶
2.7
香樟树
2.4
桂花树
23
将测量和计算的结果与树叶的形状对照,你还有什么发现?与同伴交流。
新知讲解
柳树叶
10.3
柳树叶
10.2
榆树叶
2.5
榆树叶
2.7
香樟树
2.4
桂花树
23
同一种树叶,长与宽的比值都比较接近。
比值接近的不同树叶,形状也相似。
树叶长与宽的比值越大,树叶就越狭长。
新知讲解
如果把桃树叶想像成和它同长同宽的长方形。
随着比值越来越大,长方形的形状会怎样
随着比值越来越大,长方形的长越来越长, 宽越来越短,最后变成了一条横着的线。
新知讲解
我们称它为松针。其实,树叶的很多特征有时就藏在它的名字里。
新知讲解
如果我们继续想象, 当比值越来越小呢?
随着比值越来越小,长方形的长越来越短,宽越来越长,最后变成了一条竖着的线。
新知讲解
通过这次活动,你有什么收获?
自然界中隐藏很多有趣的规律。
通过测量、计算和比较,可以帮助我们分析问题、解决问题。
善于观察和思考,才能发现和提出生活中的数学问题。
课堂练习
星期天,小刚和他的小伙伴在同一棵树下各采集了一些树叶,分别量出树叶的长和宽。
编号 ① ② ③ ④
长/mm 18 33 63 112
宽/mm 8 15 29 53
比值
1.求出每片树叶长与宽的比值(得数保留一位小数),填入表中。
2.3
2.2
2.2
2.1
课堂练习
2.
在这棵树上,小明采集了一片长145毫米的树叶,这片树叶的宽大约是多少毫米 (得数保留整数)
(2.3+2.2+2.2+2.1)÷4=2.2
145÷2.2≈66(毫米)
答:这片树叶的宽大约是66毫米。
课堂练习
3.在这棵树上,小芳采集了一片宽46毫米的树叶,这片树叶的长大约是多少毫米?(得数保留整数)
(2.3+2.2+2.2+2.1)÷4=2.2
46×2.2≈101(毫米)
答:这片树叶的长大约是101毫米。
课堂练习
4.拓展练习:小秋采集了一片树叶,量得长与宽分别是126毫米和14毫米,你认为这片树叶是小伙伴采集树口的那棵树上摘的吗 为什么
126毫米:14毫米=9
答:同一种树叶,长和宽的比值比较接近,但是这片树叶的长与宽的比值与所采集树叶长与宽的比值相差太大,所以不是是小伙伴采集树口的那棵树上摘的。
课堂练习
你知道吗?
黄金比例,又称黄金分割比,大约值为0.618。黄金分割具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值,而且呈现于不少动物和植物的外观。
课堂总结
通过今天的学习,你有哪些收获?
我知道按比例分配问题的特点了。
我学会解决按比例分配的问题了。
板书设计
树叶中的比
同一种树叶,长和宽的比值比较接近。 测量
比值接近的不同树叶,它们的形状也是相似的。 计算
树叶长与宽的比值越大,树叶就越狭长。 比较
作业布置
测量一下自己的上身与下身的长度并求比值,看看是不是黄金比。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
树叶中的比
苏教版六年级上册
教学目标
1.学习目标描述:通过观察、测量、计算、比较、分析等活动,探索并发现一些常见树叶的长与宽的比,感受到树叶的形状与它的长与宽的比之间的关系,进一步积累数学活动经验,发展数据分析观念,增强探索意识和创新意识。
2.学习内容分析:这部分内容是在学生掌握了比的相关知识,特别是学习了如何求比值之后安排的一个实践活动——测量树叶中的比。通过测量、比较同一种树叶的长和宽的比值, 发现树叶中隐藏的秘密。比如同一种树叶,长和宽的比值都比较接近;比值接近的不同树
教学目标
叶, 形状也相似;树叶长与宽的比值越大,树叶就越狭长等等。让学生在动手操作的过程中进一步体验比在现实生活中的应用,加强学生对比的认识。
3.学科核心素养分析:使学生能积极愉悦地参与探究活动,并在探索、发现树叶中有关规律的活动中,初步感受自然现象中蕴含的简单规律,培养用数学眼光观察生活的意识和能力, 感受数学活动的意义及价值,强学习数学、应用数学的兴趣。
新知导入
1.填一填。
长方形长与宽的比是( ),比值是( )。
长方形宽与长的比是( ),比值是( )。
16厘米
6厘米
8:3
8
3
3:8
3
8
新知导入
怎样求出两个数的比值?
用比的前项除以比的后项所得的商就是比值,比值可以是分数,也可以是小数,还可以是整数。
新知导入
2.求比值。
0.08:0.5 1.2米:60厘米 :
1
6
1
10
=0.08÷0.5
=0.16
=120厘米:60厘米
=120÷60
=2
= ÷
1
6
1
10
= ×
1
6
10
=
5
3
新知导入
猜
一
猜
春来穿新衣,
秋来换新装。
夏至刷绿漆,
冬至落满地。
(打一植物构造)
新知导入
树叶对于我们来说非常熟悉,在我们生活中随处可见。树叶可以为我们提供氧气,从而达到净化空气的效果,也给我们带来了美的享受。
新知讲解
你认识这些树叶吗?
柳树叶
桃树叶
香樟树叶
枇杷树叶
桑树叶
银杏树叶
槐树叶
枫树叶
新知讲解
观察这些树叶,你有什么想法?说说这些树叶有什么不同?
树叶有大有小,有长长的,有圆圆的… …
不同的树,树叶的形状一般是不同的。
相同的树,树叶虽然大小不同,但形状相似。
新知讲解
还可以怎样比较这些树叶的形状?和同学说说你的想法。
可以测量每片树叶的长和宽,再比较。
可以算出同一种树叶长与宽的比值,再比较。
可以算出不同树的树叶长与宽的比值, 再比较。
新知讲解
你知道吗?
测量、计算和比较都是我们探究数学问题的常用方法。
新知讲解
你知道怎么测量树叶的长和宽吗?指一指下面两片树叶的长和宽该如何测量。
树叶的长一般是指沿主叶脉方向量出的最长距离的长度(不含叶柄),宽一般是指树叶中沿与主叶脉垂直方向量出的最宽处。
新知讲解
长
宽
长
宽
选择一片喜欢的树叶, 指一指它的长和宽。
新知讲解
活动要求:
(1)每组测量同一种树的树叶(10片), 组长明确分工。
(2)量出每一片树叶的长和宽,算出长与宽的比值(得数保留一位小数),填入右表。
新知讲解
( )树叶的长和宽及比值
香樟树
编号 长/mm 宽/mm 比值 编号 长/mm 宽/mm 比值
1 370 150 2.5 6 360 152 2.4
2 550 220 2.5 7 180 74 2.4
3 960 420 2.3 8 251 105 2.4
4 136 58 2.3 9 78 29 2.3
5 121 50 2.4 10 222 100 2.2
新知讲解
( )树叶的长和宽及比值
柳树
编号 长/mm 宽/mm 比值 编号 长/mm 宽/mm 比值
1 543 52 10.3 6 621 61 10.3
2 277 29 10.2 7 704 68 10.4
3 102 10 10.2 8 230 22 10.3
4 410 42 10 9 147 14 10.5
5 56 6 10.2 10 201 20 10.2
新知讲解
分小组计算各自测量的10片树叶长与宽比值的平均数(得数保留一位小数)。
柳树叶
10.3
柳树叶
10.2
榆树叶
2.5
榆树叶
2.7
香樟树
2.4
桂花树
23
将测量和计算的结果与树叶的形状对照,你还有什么发现?与同伴交流。
新知讲解
柳树叶
10.3
柳树叶
10.2
榆树叶
2.5
榆树叶
2.7
香樟树
2.4
桂花树
23
同一种树叶,长与宽的比值都比较接近。
比值接近的不同树叶,形状也相似。
树叶长与宽的比值越大,树叶就越狭长。
新知讲解
如果把桃树叶想像成和它同长同宽的长方形。
随着比值越来越大,长方形的形状会怎样
随着比值越来越大,长方形的长越来越长, 宽越来越短,最后变成了一条横着的线。
新知讲解
我们称它为松针。其实,树叶的很多特征有时就藏在它的名字里。
新知讲解
如果我们继续想象, 当比值越来越小呢?
随着比值越来越小,长方形的长越来越短,宽越来越长,最后变成了一条竖着的线。
新知讲解
通过这次活动,你有什么收获?
自然界中隐藏很多有趣的规律。
通过测量、计算和比较,可以帮助我们分析问题、解决问题。
善于观察和思考,才能发现和提出生活中的数学问题。
课堂练习
星期天,小刚和他的小伙伴在同一棵树下各采集了一些树叶,分别量出树叶的长和宽。
编号 ① ② ③ ④
长/mm 18 33 63 112
宽/mm 8 15 29 53
比值
1.求出每片树叶长与宽的比值(得数保留一位小数),填入表中。
2.3
2.2
2.2
2.1
课堂练习
2.
在这棵树上,小明采集了一片长145毫米的树叶,这片树叶的宽大约是多少毫米 (得数保留整数)
(2.3+2.2+2.2+2.1)÷4=2.2
145÷2.2≈66(毫米)
答:这片树叶的宽大约是66毫米。
课堂练习
3.在这棵树上,小芳采集了一片宽46毫米的树叶,这片树叶的长大约是多少毫米?(得数保留整数)
(2.3+2.2+2.2+2.1)÷4=2.2
46×2.2≈101(毫米)
答:这片树叶的长大约是101毫米。
课堂练习
4.拓展练习:小秋采集了一片树叶,量得长与宽分别是126毫米和14毫米,你认为这片树叶是小伙伴采集树口的那棵树上摘的吗 为什么
126毫米:14毫米=9
答:同一种树叶,长和宽的比值比较接近,但是这片树叶的长与宽的比值与所采集树叶长与宽的比值相差太大,所以不是是小伙伴采集树口的那棵树上摘的。
课堂练习
你知道吗?
黄金比例,又称黄金分割比,大约值为0.618。黄金分割具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值,而且呈现于不少动物和植物的外观。
课堂总结
通过今天的学习,你有哪些收获?
我知道按比例分配问题的特点了。
我学会解决按比例分配的问题了。
板书设计
树叶中的比
同一种树叶,长和宽的比值比较接近。 测量
比值接近的不同树叶,它们的形状也是相似的。 计算
树叶长与宽的比值越大,树叶就越狭长。 比较
作业布置
测量一下自己的上身与下身的长度并求比值,看看是不是黄金比。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
