人教版(新)五上 第五单元 5.解方程 第一课时【优质课件】
文档属性
| 名称 | 人教版(新)五上 第五单元 5.解方程 第一课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 17:19:56 | ||
图片预览








文档简介
(共23张PPT)
解方程
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
01
课前导入
目录
02
新课精讲
03
学以致用
04
课堂小结
01
课前导入
情景导入
1.4x=9.8 ( )
√
3x-8y=14 ( )
16+y<30 ( )
下面哪个式子是方程?
×
21÷7=3 ( )
√
×
02
新课精讲
探索新知
探究点 1
形如x+a=b的方程的解法
问题:1. 你能根据图意列出方程吗?你是怎么想的?
x+3=9
2. x代表几呢?请你运用所学的知识试着确定x
的值,并写出过程。
9个
探索新知
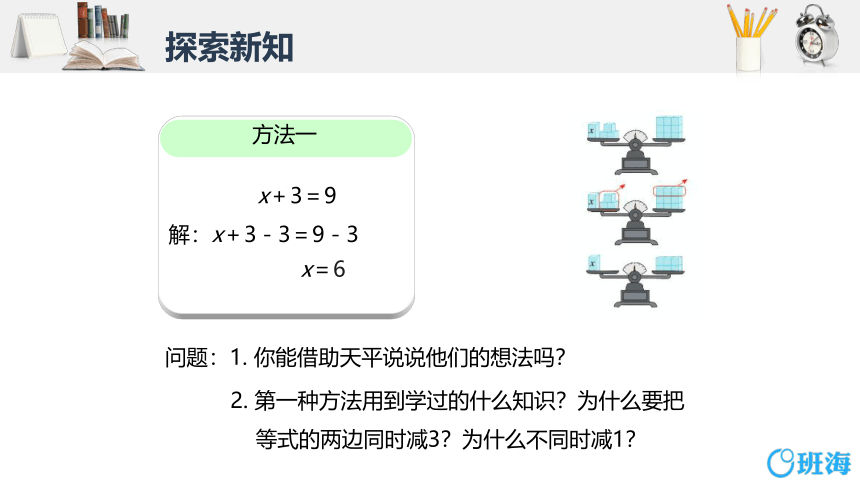
方法一
x+3=9
解:x+3-3=9-3
x=6
问题:1. 你能借助天平说说他们的想法吗?
2. 第一种方法用到学过的什么知识?为什么要把
等式的两边同时减3?为什么不同时减1?
探索新知
x+3=9
解: x=9-3
x=6
问题:你理解这种方法吗?请说说理由。
把方程x+3=9看作一个加法算式, x和3是两个加数,9是和;根据加法中各部分之间的关系:加数=和-加数得: x=9-3。
提示:
方法二
探索新知
方法一
x+3=9
解: x+3-3=9-3
x=6
方法二
x+3=9
解: x=9-3
x=6
对比:两种不同的方法有什么异同点?
提示:
在小学阶段,特别是刚刚学习解方程时,我们通常选用方法一解方程,方法二也可以看作是方法一的简写形式。
探索新知
方法归纳:
形如x+a=b的方程的解法:
1.先写“解:”;
2. 在方程的两边同时减去a,使等式成立;
3.求出x的值。
探索新知
探究点 2
方程的解和解方程的意义
x+3=9
解: x+3-3=9-3
x=6
思考:
1.结合上例,说一说什么是解方程?什么是方程的解?
2.方程的解和解方程有什么区别?
求方程的解的过程叫做解方程。
使方程左右两边相等的未知数的值,叫做方程的解。
方程的解是一个数值,而解方程是一个过程。
探索新知
怎样检验一下答案是否正确呢?
x+3=9
解: x+3-3=9-3
=6+3
=9
=方程右边
所以,x=6是方程的解。
方程左边=x+3
x=6
探索新知
方法归纳:
1.使方程左右两边相等的未知数的值,叫做方程的解。
2.求方程的解的过程叫做解方程。
3.方程的解是一个数值,而解方程是一个过程。
典题精讲
1. 解方程。
解:x-63+63=36+63
x=99
2. 小诊所。
x-18=18
解: x=18-18
x=0
x=36
改正:
解: x=18+18
x-63=36
典题精讲
3. x=2是方程5x=15的解吗?x=3呢?
方程左边=5x
=5×2
=10
≠方程右边
所以,x=2不是方程的解。
方程左边=5x
=5×3
=15
=方程右边
所以,x=3是方程的解。
典题精讲
(1)等式就是方程。 ( )
(2)含有未知数的式子叫做方程。 ( )
(3)方程一定是等式,等式不一定是方程。 ( )
(4)x=0是方程8x=0的解。 ( )
(5)方程的解和解方程的意义相同。 ( )
√
√
4.判断。
×
×
×
03
学以致用
小试牛刀
1.填一填。
x+0.5=2.5
解:x+0.5-( )= 2.5-( )
x= ( )
(1)使方程左右两边相等的未知数的值,叫做方程的( ),
在上面的方程中,x=( )是方程的解。
(2)求方程的解的过程叫做( )。
0.5
0.5
2
解
2
解方程
小试牛刀
2.后面( )中哪个x的值是方程的解?用横线画出来。
(1)x+19=21 (x=2,x=40)
(2)15-x=7 (x=22,x=8)
(3)6x=9 (x=1.5,x=2)
(4)6÷x=3 (x=2,x=0.2)
小试牛刀
3.解下列方程并检验。
28+x=48
解: 28+x-28=48-28
x=20
检验: 方程左边=28+x
=28+20
=48
=方程右边
所以,x=20是方程的解。
解:x+1.2-1.2=2.5-1.2
x=1.3
检验: 方程左边=x+1.2
=1.3+1.2
=2.5
=方程右边
所以,x=1.3是方程的解。
x+1.2=2.5
04
课堂小结
归纳总结:
1.形如x+a=b的方程的解法:运用等式的性质1,在方程的左右两
边同时减去a,可得到方程的解。
2.方程的解:使方程左右两边相等的未知数的值,叫做方程的解。
3.解方程:求方程的解的过程叫做解方程。
4.方程的解是一个数值,而解方程是一个过程。
同学们,下节课见!
一键发布配套作业 & AI智能精细批改
(↓↓观看介绍视频↓↓)
解方程
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
01
课前导入
目录
02
新课精讲
03
学以致用
04
课堂小结
01
课前导入
情景导入
1.4x=9.8 ( )
√
3x-8y=14 ( )
16+y<30 ( )
下面哪个式子是方程?
×
21÷7=3 ( )
√
×
02
新课精讲
探索新知
探究点 1
形如x+a=b的方程的解法
问题:1. 你能根据图意列出方程吗?你是怎么想的?
x+3=9
2. x代表几呢?请你运用所学的知识试着确定x
的值,并写出过程。
9个
探索新知
方法一
x+3=9
解:x+3-3=9-3
x=6
问题:1. 你能借助天平说说他们的想法吗?
2. 第一种方法用到学过的什么知识?为什么要把
等式的两边同时减3?为什么不同时减1?
探索新知
x+3=9
解: x=9-3
x=6
问题:你理解这种方法吗?请说说理由。
把方程x+3=9看作一个加法算式, x和3是两个加数,9是和;根据加法中各部分之间的关系:加数=和-加数得: x=9-3。
提示:
方法二
探索新知
方法一
x+3=9
解: x+3-3=9-3
x=6
方法二
x+3=9
解: x=9-3
x=6
对比:两种不同的方法有什么异同点?
提示:
在小学阶段,特别是刚刚学习解方程时,我们通常选用方法一解方程,方法二也可以看作是方法一的简写形式。
探索新知
方法归纳:
形如x+a=b的方程的解法:
1.先写“解:”;
2. 在方程的两边同时减去a,使等式成立;
3.求出x的值。
探索新知
探究点 2
方程的解和解方程的意义
x+3=9
解: x+3-3=9-3
x=6
思考:
1.结合上例,说一说什么是解方程?什么是方程的解?
2.方程的解和解方程有什么区别?
求方程的解的过程叫做解方程。
使方程左右两边相等的未知数的值,叫做方程的解。
方程的解是一个数值,而解方程是一个过程。
探索新知
怎样检验一下答案是否正确呢?
x+3=9
解: x+3-3=9-3
=6+3
=9
=方程右边
所以,x=6是方程的解。
方程左边=x+3
x=6
探索新知
方法归纳:
1.使方程左右两边相等的未知数的值,叫做方程的解。
2.求方程的解的过程叫做解方程。
3.方程的解是一个数值,而解方程是一个过程。
典题精讲
1. 解方程。
解:x-63+63=36+63
x=99
2. 小诊所。
x-18=18
解: x=18-18
x=0
x=36
改正:
解: x=18+18
x-63=36
典题精讲
3. x=2是方程5x=15的解吗?x=3呢?
方程左边=5x
=5×2
=10
≠方程右边
所以,x=2不是方程的解。
方程左边=5x
=5×3
=15
=方程右边
所以,x=3是方程的解。
典题精讲
(1)等式就是方程。 ( )
(2)含有未知数的式子叫做方程。 ( )
(3)方程一定是等式,等式不一定是方程。 ( )
(4)x=0是方程8x=0的解。 ( )
(5)方程的解和解方程的意义相同。 ( )
√
√
4.判断。
×
×
×
03
学以致用
小试牛刀
1.填一填。
x+0.5=2.5
解:x+0.5-( )= 2.5-( )
x= ( )
(1)使方程左右两边相等的未知数的值,叫做方程的( ),
在上面的方程中,x=( )是方程的解。
(2)求方程的解的过程叫做( )。
0.5
0.5
2
解
2
解方程
小试牛刀
2.后面( )中哪个x的值是方程的解?用横线画出来。
(1)x+19=21 (x=2,x=40)
(2)15-x=7 (x=22,x=8)
(3)6x=9 (x=1.5,x=2)
(4)6÷x=3 (x=2,x=0.2)
小试牛刀
3.解下列方程并检验。
28+x=48
解: 28+x-28=48-28
x=20
检验: 方程左边=28+x
=28+20
=48
=方程右边
所以,x=20是方程的解。
解:x+1.2-1.2=2.5-1.2
x=1.3
检验: 方程左边=x+1.2
=1.3+1.2
=2.5
=方程右边
所以,x=1.3是方程的解。
x+1.2=2.5
04
课堂小结
归纳总结:
1.形如x+a=b的方程的解法:运用等式的性质1,在方程的左右两
边同时减去a,可得到方程的解。
2.方程的解:使方程左右两边相等的未知数的值,叫做方程的解。
3.解方程:求方程的解的过程叫做解方程。
4.方程的解是一个数值,而解方程是一个过程。
同学们,下节课见!
一键发布配套作业 & AI智能精细批改
(↓↓观看介绍视频↓↓)
