4.4对数函数 辅导教案(表格式)
文档属性
| 名称 | 4.4对数函数 辅导教案(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 501.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 00:00:00 | ||
图片预览



文档简介
个性化教学设计
学生姓名 年级 高一 学科 数学
课题 对数函数
教学目标 掌握对数函数的概念
重点难点 比较大小、求定义域值域
考点分析 基本技能的考察
教学流程
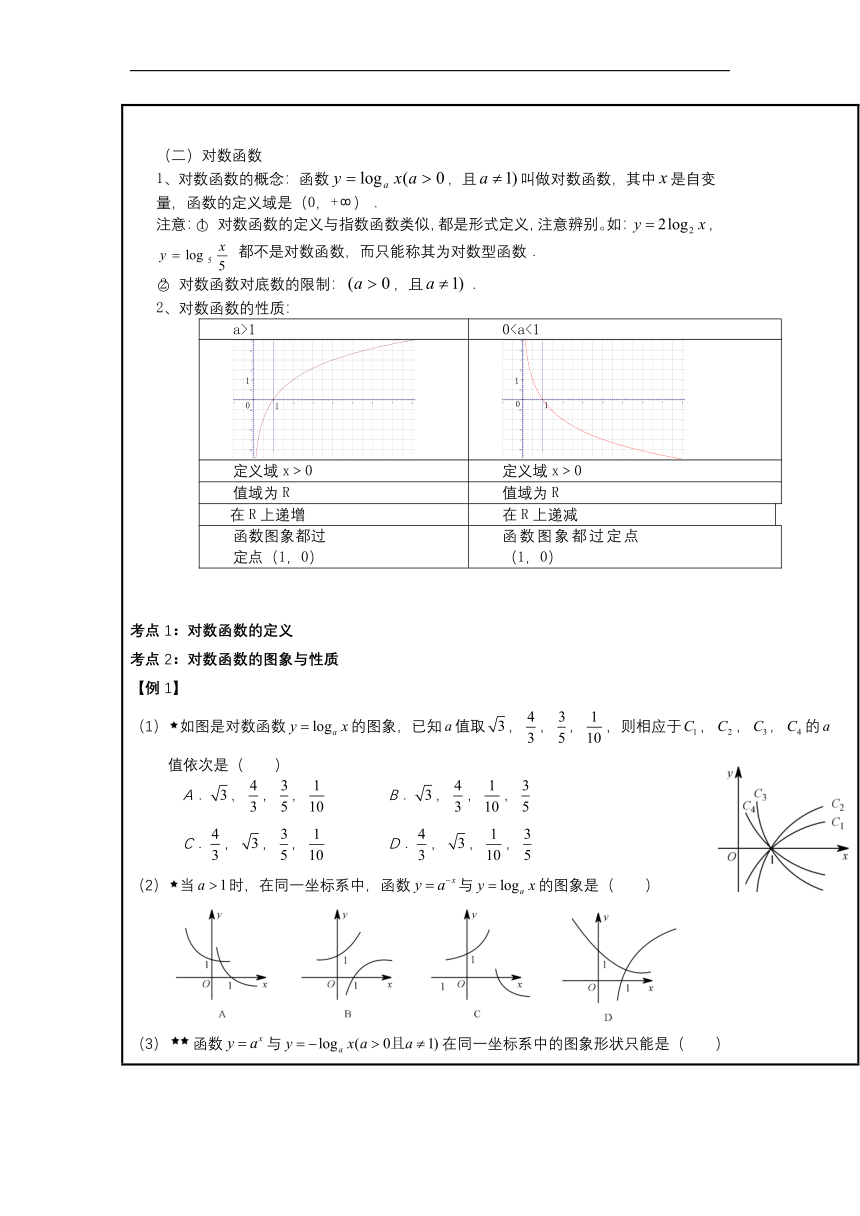
(一)对数 1.对数的概念:一般地,如果,那么数叫做以为底的对数,记作:(— 底数,— 真数,— 对数式) 说明: 注意底数的限制,且; ; 注意对数的书写格式. 两个重要对数: 常用对数:以10为底的对数; 自然对数:以无理数为底的对数的对数. 指数式与对数式的互化 幂值 真数 = N= b 底数 指数 对数 (二)对数的运算性质 如果,且,,,那么: ·+; -; . 注意:换底公式 (,且;,且;). 利用换底公式推导下面的结论 (1); (2). 考点1:指数式与对数式的互化 【例1】将下列指数式化为对数式,对数式化为指数式 ① ; ② ; ③ ; ④ ; ⑤ ; ⑥ . 【例2】求下列各式中的值 ; ② ; ③; ④ ; ⑤; ⑥; 考点2:对数恒等式及对数性质 【例3】 (1)下列等式中正确的是( ) A. B. C. D. (2)求下列各值: ① ; ② ; ③ ; ④ ; ⑤ ; ⑥ ; ⑦ ; ⑧ ; ⑨ . (3)已知,求实数的值. 考点3:对数的运算性质 【例4】 (1) 用,,表示下列各式 ① ____________; ② ____________; ③ ____________; ④ ____________. (2)计算下列各式 ① _____;② _____;③ _____; ④ _____;⑤ ______; ⑥ ________. 考点4:换底公式 【例5】计算下列各式 ①________;②________; ③_________; ④_______. 【例6】 (1)已知,请用表示 (2)已知,那么______(用表示); (3),,那么______(用,表示); 【速算】求值: (1)= (2)= (3)= (4)= (5)= (6)= (7)= (8)= (9)= (10)= (11) (12) (13) (二)对数函数 1、对数函数的概念:函数,且叫做对数函数,其中是自变量,函数的定义域是(0,+∞). 注意: 对数函数的定义与指数函数类似,都是形式定义,注意辨别。如:, 都不是对数函数,而只能称其为对数型函数. 对数函数对底数的限制:,且. 2、对数函数的性质: a>10考点1:对数函数的定义 考点2:对数函数的图象与性质 【例1】 (1)如图是对数函数的图象,已知值取,,,,则相应于,,,的 值依次是( ) A.,,, B.,,, C.,,, D.,,, (2)当时,在同一坐标系中,函数与的图象是( ) (3)函数与在同一坐标系中的图象形状只能是( ) 考点3:对数值的大小比较 【例2】比较下列各题中两个值的大小 (1)与 (2)与 (3)和 (4)和 (5)和 (6)和 (7)和 (8)与 (9)与 (10)与 (11)和 【例3】 (1)比较大小(填“”,“”或“”). ①____;②____;③____ ④____; ⑤____; ⑥____. (2)若,,,则( ) A. B. C. D. (3)若,,,则( ) A. B. C. D. 【拓展】 (1)设,,,则的大小顺序是( ) A. B. C. D. (2)设,,,则的大小顺序是( ) A. B. C. D. 考点4:对数函数与指数函数的关系 【例4】判断下列函数是否有反函数,若有,则求出反函数 (1);(2);(3);(4);(5);(6) 【例5】 (1)若,,且,,.则与的图象( ) A.关于直线对称 B.关于直线对称 C.关于轴对称 D.关于原点对称 (2)若函数(,且)的反函数的图象过点,则______. (3)若的反函数是,则值为( ) A.3 B. C. D. 考点5:与对数相关的复合函数的定义域问题 【例6】求下列函数的定义域 ①;②;③. 【例7】求下列函数的定义域 ①;②;③; ④;⑤. 考点6:与对数相关的复合函数的值域问题 【例8】 (1)已知函数,①当时,函数值域为____________;②当时,函数值 域为____________;③当时,函数值域为____________. (2)已知函数,①当时,函数值域为_____________;②当时,函数 值域为______________;③当时,函数值域为______________; 【例9】求下列函数的值域 (1);(2);(3); (4);(5);(6). 【例10】已知函数. (1)若的定义域为,求实数的范围; (2)若的值域为,求实数的范围. 考点7:与对数相关的复合函数的单调性问题 【例11】判断下列函数的单调性 (1);(2);(3); (4);(5) 【例12】求函数的定义域、值域和单调区间.
课堂总结
效果评价 知识理解 ( ) 应用能力( )
课时确认 __________年_____月_____日 _______:_______ 计______课时
学生签字 教师签字
教案审核(盖章) 审核人(签章)
学生姓名 年级 高一 学科 数学
课题 对数函数
教学目标 掌握对数函数的概念
重点难点 比较大小、求定义域值域
考点分析 基本技能的考察
教学流程
(一)对数 1.对数的概念:一般地,如果,那么数叫做以为底的对数,记作:(— 底数,— 真数,— 对数式) 说明: 注意底数的限制,且; ; 注意对数的书写格式. 两个重要对数: 常用对数:以10为底的对数; 自然对数:以无理数为底的对数的对数. 指数式与对数式的互化 幂值 真数 = N= b 底数 指数 对数 (二)对数的运算性质 如果,且,,,那么: ·+; -; . 注意:换底公式 (,且;,且;). 利用换底公式推导下面的结论 (1); (2). 考点1:指数式与对数式的互化 【例1】将下列指数式化为对数式,对数式化为指数式 ① ; ② ; ③ ; ④ ; ⑤ ; ⑥ . 【例2】求下列各式中的值 ; ② ; ③; ④ ; ⑤; ⑥; 考点2:对数恒等式及对数性质 【例3】 (1)下列等式中正确的是( ) A. B. C. D. (2)求下列各值: ① ; ② ; ③ ; ④ ; ⑤ ; ⑥ ; ⑦ ; ⑧ ; ⑨ . (3)已知,求实数的值. 考点3:对数的运算性质 【例4】 (1) 用,,表示下列各式 ① ____________; ② ____________; ③ ____________; ④ ____________. (2)计算下列各式 ① _____;② _____;③ _____; ④ _____;⑤ ______; ⑥ ________. 考点4:换底公式 【例5】计算下列各式 ①________;②________; ③_________; ④_______. 【例6】 (1)已知,请用表示 (2)已知,那么______(用表示); (3),,那么______(用,表示); 【速算】求值: (1)= (2)= (3)= (4)= (5)= (6)= (7)= (8)= (9)= (10)= (11) (12) (13) (二)对数函数 1、对数函数的概念:函数,且叫做对数函数,其中是自变量,函数的定义域是(0,+∞). 注意: 对数函数的定义与指数函数类似,都是形式定义,注意辨别。如:, 都不是对数函数,而只能称其为对数型函数. 对数函数对底数的限制:,且. 2、对数函数的性质: a>10
课堂总结
效果评价 知识理解 ( ) 应用能力( )
课时确认 __________年_____月_____日 _______:_______ 计______课时
学生签字 教师签字
教案审核(盖章) 审核人(签章)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
