12.3乘法公式 自主达标测试题 2022-2023学年华东师大版八年级数学上册(Word版含答案)
文档属性
| 名称 | 12.3乘法公式 自主达标测试题 2022-2023学年华东师大版八年级数学上册(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 95.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-11 17:00:53 | ||
图片预览




文档简介
2022-2023学年华东师大版八年级数学上册《12.3乘法公式》自主达标测试题(附答案)
一.选择题(共8小题,满分32分)
1.已知(3x+a)2=9x2+bx+4,则b的值为( )
A.4 B.±6 C.12 D.±12
2.已知x+y=﹣6,xy=8,则x2+y2的值为( )
A.36 B.32 C.20 D.8
3.若x2﹣2mx+16是完全平方式,则m的值等于( )
A.2 B.2或﹣2 C.4或﹣4 D.8或﹣8
4.若M(3a﹣b2)=b4﹣9a2,那么代数式M应是( )
A.﹣3a+b2 B.3a+b2 C.3a﹣b2 D.﹣3a﹣b2
5.已知(a+b)2=28,(a﹣b)2=12,则a2+b2的值为( )
A.8 B.16 C.20 D.40
6.如图1,从边长为a的大正方形纸片中挖去一个边长为b的小正方形纸片后,将其沿实线裁成两个相同的直角梯形,然后拼成一个等腰梯形(如图2),则通过计算图形阴影部分的面积,可以验证成立的公式是( )
A.(a﹣b)2=a2﹣b2 B.(a﹣b)2=a2﹣2ab+b2
C.(a+b)2=a2+2ab+b2 D.a2﹣b2=(a+b)(a﹣b)
7.如图,M是AG的中点,B是AG上一点.分别以AB、BG为边,作正方形ABCD和正方形BGFE,连接MD和MF.设AB=a,BG=b,且a+b=10,ab=21,则图中阴影部分的面积为( )
A.46 B.33 C.28 D.52
8.若x满足(x﹣2021)(2022﹣x)=0.25,则(x﹣2021)2+(2022﹣x)2=( )
A.0.25 B.0.5 C.1 D.﹣0.25
二.填空题(共10小题,满分40分)
9.计算:(﹣m+n)(﹣m﹣n)= .
10.一个正方形的边长增加了3cm,面积相应增加了39cm2,则原来这个正方形的边长为 cm.
11.若a(a﹣1)﹣(a2﹣b)=4,则的值是 .
12.若x2+(m﹣3)x+9是完全平方式,则m= .
13.如图是一个正方形,分成四部分,其面积分别为a2,ab,ab,b2,则原正方形的边长是 .
14.(1)已知x+y=4,xy=3,则x2+y2的值为 .
(2)已知(x+y)2=25,x2+y2=17,则(x﹣y)2的值为 .
(3)已知x满足(x﹣2020)2+(2022﹣x)2=12,则(x﹣2021)2的值为 .
15.若(x+9y)2=(x﹣9y)2+A,则代数式A为 .
16.若2a﹣b=2,则4a2﹣b2﹣4b的值是 .
17.边长为a的正方形ABCD与边长为b的正方形DEFG按如图所示的方式摆放,点A,D,G在同一直线上.已知a+b=10,ab=24.则图中阴影部分的面积为 .
18.计算:(2b﹣3c+4)(3c﹣2b+4)﹣2(b﹣c)2= .
三.解答题(共7小题,满分48分)
19.计算:(9x﹣2y)(x+y)﹣(﹣3x+y)(﹣3x﹣y).
20.(﹣2y+1)2﹣(2y+1)(2y﹣1).
21.要求:利用乘法公式计算.
(1)2023×2021﹣20222;
(2)(2x﹣y+3)(2x﹣y﹣3).
22.若x、y满足x2+y2=,xy=﹣,求下列各式的值.
(1)(x+y)2
(2)x4+y4.
23.阅读例题的解答过程,并解答下列各题.
例:用简便方法计算103×97.
解:103×97=(100+3)(100﹣3)①=1002﹣32②=9991.
(1)例题求解过程中,第②步变形的依据是 ;
(2)用简便方法计算9×11×101;
(3)用简便方法计算20212﹣2020×2022.
24.在课后服务课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b,宽为α的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
【发现】
(1)根据图2,写出一个我们熟悉的数学公式 .
【应用】
(2)根据(1)中的数学公式,解决如下问题:
①已知:a+b=7,a2+b2=25,求ab的值.
②如果一个长方形的长和宽分别为(8﹣x)和(x﹣2),且(8﹣x)2+(x﹣2)2=20,求这个长方形的面积.
25.若x满足(9﹣x)(x﹣4)=4,求(4﹣x)2+(x﹣9)2的值.
解:设9﹣x=a,x﹣4=b,则(9﹣x)(x﹣4)=ab=4,a+b=(9﹣x)+(x﹣4)=5,
∴(9﹣x)2+(x﹣4)2=a2+b2﹣2ab=52﹣2×4=17.
请仿照上面的方法求解下面问题:
(1)若x满足(5﹣x)(x﹣2)=2,求(5﹣x)2+(x﹣2)2的值.
(2)若x满足(6﹣x)(3﹣x)=1,求代数式(9﹣2x)2的值.
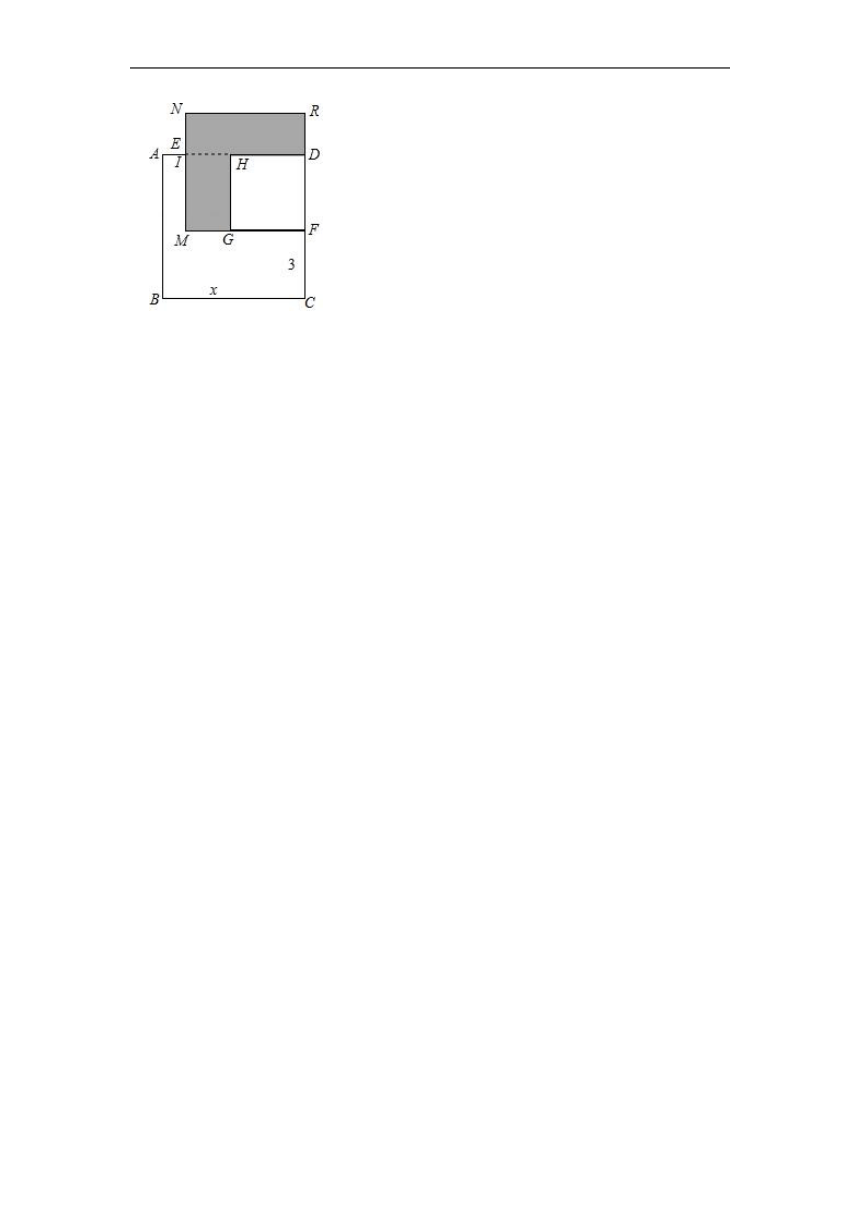
(3)已知正方形ABCD的边长为x,E,F分别是AD、DC上的点,且AE=3,CF=5,长方形EMFD的面积是48,分别以MF、DF作正方形,求阴影部分的面积.
参考答案
一.选择题(共8小题,满分32分)
1.解:∵(3x±2)2=9x2±12x+4,
∴b=±12,
故选:D.
2.解:x2+y2
=(x+y)2﹣2xy
=(﹣6)2﹣2×8
=20,
故选:C.
3.解:∵(x±4)2=x2±8x+16,
∴﹣2m=±8,
∴m=±4,
故选:C.
4.解:M===﹣b2﹣3a,
故选:D.
5.解:∵(a+b)2=28,(a﹣b)2=12,
∴a2+b2+2ab=28①,a2+b2﹣2ab=12②,
∴①+②得:
2(a2+b2)=40,
∴a2+b2=20,
故选:C.
6.解:∵图形中阴影部分的面积可表示为a2﹣b2或=(a+b)(a﹣b),
∴a2﹣b2=(a+b)(a﹣b),
故选:D.
7.解:∵(a+b)2=a2+2ab+b2,
∴a2+b2=(a+b)2﹣2ab,
由题意得,图中阴影部分的面积为:
a2+b2﹣(+)
=(a+b)2﹣2ab﹣,
=﹣2ab,
∴当a+b=10,ab=21时,
原式=﹣2×21
=75﹣42
=33,
故选:B.
8.解:(x﹣2021)2+(2022﹣x)2
=(x﹣2021+2022﹣x)2﹣2(x﹣2021)(2022﹣x)
=1﹣2×0.25
=0.5,
故选:B.
二.填空题(共10小题,满分40分)
9.解:原式=(﹣m)2﹣n2
=(m)2﹣n2,
=m2﹣n2
故答案为:m2﹣n2.
10.解:设原来正方形的边长是xcm.根据题意得:
(x+3)2﹣x2=39,
∴(x+3+x)(x+3﹣x)=3(2x+3)=39,
解得x=5.
11.解:∵a(a﹣1)﹣(a2﹣b)=4,
∴a2﹣a﹣a2+b=4,
∴b﹣a=4,
∴====8.
故答案为:8.
12.解:∵x2+(m﹣3)x+9是完全平方式,
∴m﹣3=±6,
解得:m=9或﹣3.
故答案为:9或﹣3.
13.解:原正方形的面积为a2+2ab+b2=(a+b)2,
所以原正方形的边长是a+b,
故答案为:a+b.
14.解:(1)∵x+y=4,xy=3,
∴x2+y2=(x+y)2﹣2xy=16﹣6=10.
故答案为:10;
(2)∵(x+y)2=25,x2+y2=17,
∴x2+y2+2xy﹣(x2+y2)=8,
∴xy=4,
∴(x﹣y)2=x2+y2﹣2xy=17﹣8=9.
故答案为:9;
(3)∵(x﹣2020)2+(x﹣2022)2=12,
∴[(x﹣2021)+1]2+[(x﹣2021)﹣1]2=12,
∴(x﹣2021)2+2(x﹣2021)+1+(x﹣2021)2﹣2(x﹣2021)+1=12,
∴(x﹣2021)2=5.
故答案为:5.
15.解:因为(x+9y)2=x2+18xy+81y2,(x﹣9y)2=x2﹣18xy+81y2,
所以(x+9y)2=x2﹣18xy+81y2+36xy=(x﹣9y)2+36xy,
因为(x+9y)2=(x﹣9y)2+A,
所以A=36xy.
故答案为:36xy.
16.解:∵2a﹣b=2,
∴原式=(2a﹣b)(2a+b)﹣4b=2(2a+b)﹣4b
=4a+2b﹣4b
=4a﹣2b
=2(2a﹣b)
=2×2
=4.
故答案为:4.
17.解:由S阴影部分=S正方形ABCD+S正方形DEFG﹣S△ABC﹣S△AFG可得,
S阴影部分=a2+b2﹣a2﹣b(a+b)
=a2+b2﹣ab
=(a2+b2﹣ab)
=[(a+b)2﹣3ab]
=×(100﹣72)
=14,
故答案为:14.
18.解:(2b﹣3c+4)(3c﹣2b+4)﹣2(b﹣c)2,
=[(2b﹣3c)+4][﹣(2b﹣3c)+4]﹣2(b﹣c)2,
=16﹣(2b﹣3c)2﹣2(b﹣c)2,
=16﹣4b2+12bc﹣9c2﹣2b2+4bc﹣2c2,
=﹣6b2﹣11c2+16bc+16.
三.解答题(共7小题,满分48分)
19.解:(9x﹣2y)(x+y)﹣(﹣3x+y)(﹣3x﹣y)
=9x2+9xy﹣2xy﹣2y2﹣(9x2﹣y2)
=9x2+9xy﹣2xy﹣2y2﹣9x2+y2
=7xy﹣y2.
20.解:原式=4y2﹣4y+1﹣(4y2﹣1)
=4y2﹣4y+1﹣4y2+1
=﹣4y+2.
21.解:(1)原式=(2022+1)×(2022﹣1)﹣20222
=20222﹣1﹣20222
=﹣1.
(2)原式=(2x﹣y)2﹣9
=4x2﹣4xy+y2﹣9.
22.解:(1)∵x2+y2=,xy=﹣,
∴原式=x2+y2+2xy=﹣1=;
(2)∵x2+y2=,xy=﹣,
∴原式=(x2+y2)2﹣2x2y2=﹣=.
23.解:(1)平方差公式;
(2)9×11×101
=(10﹣1)×(10+1)×101
=(100﹣1)×101
=(100﹣1)(100+1)
=1002﹣12
=9999;
(3)20212﹣2020×2022
=20212﹣(2021﹣1)(2021+1)
=20212﹣(20212﹣12)
=20212﹣20212+1
=1.
24.解:(1)由图2可知,(a+b)2=a2+2ab+b2,
故答案为:(a+b)2=a2+2ab+b2;
(2)①∵a+b=7,
∴(a+b)2=a2+2ab+b2=49,
∵a2+b2=25,
∴2ab=24,
∴ab=12;
②由(1)知,[(8﹣x)+(x﹣2)]2=(8﹣x)2+2(8﹣x)(x﹣2)+(x﹣2)2=36,
∵(8﹣x)2+(x﹣2)2=20,
∴2(8﹣x)(x﹣2)=16,
∴(8﹣x)(x﹣2)=8,
故这个长方形的面积为8.
25.解:(1)设(5﹣x)=a,(x﹣2)=b,
则(5﹣x)(x﹣2)=ab=2,
a+b=(5﹣x)+(x﹣2)=3,
∴(5﹣x)2+(x﹣2)2
=(a+b)2﹣2ab
=32﹣2×2
=5;
(2)设(6﹣x)=a,(3﹣x)=b,
(6﹣x)(3﹣x)=ab=1,
a﹣b=(6﹣x)﹣(3﹣x)=3,
∵(a+b)2
=(a﹣b)2+4ab
=13,
∴(a+b)2=13,
∵(6﹣x)+(3﹣x)=a+b,
∴9﹣2x=a+b,
∴(9﹣2x)2=(a+b)2=13.
(3)∵正方形ABCD的边长为x,AE=3,CF=5,
∴MF=DE=x﹣3,DF=x﹣5,
∴(x﹣3) (x﹣5)=48,
∴(x﹣3)﹣(x﹣5)=2,
∴阴影部分的面积=FM2﹣DF2=(x﹣3)2﹣(x﹣5)2.
设(x﹣3)=a,(x﹣5)=b,则(x﹣3)(x﹣5)=ab=48,
a﹣b=(x﹣3)﹣(x﹣5)=2,
∴a=8,b=6,a+b=14,
∴(x﹣3)2﹣(x﹣5)2=a2﹣b2=(a+b)(a﹣b)=14×2=28.
即阴影部分的面积是28.
一.选择题(共8小题,满分32分)
1.已知(3x+a)2=9x2+bx+4,则b的值为( )
A.4 B.±6 C.12 D.±12
2.已知x+y=﹣6,xy=8,则x2+y2的值为( )
A.36 B.32 C.20 D.8
3.若x2﹣2mx+16是完全平方式,则m的值等于( )
A.2 B.2或﹣2 C.4或﹣4 D.8或﹣8
4.若M(3a﹣b2)=b4﹣9a2,那么代数式M应是( )
A.﹣3a+b2 B.3a+b2 C.3a﹣b2 D.﹣3a﹣b2
5.已知(a+b)2=28,(a﹣b)2=12,则a2+b2的值为( )
A.8 B.16 C.20 D.40
6.如图1,从边长为a的大正方形纸片中挖去一个边长为b的小正方形纸片后,将其沿实线裁成两个相同的直角梯形,然后拼成一个等腰梯形(如图2),则通过计算图形阴影部分的面积,可以验证成立的公式是( )
A.(a﹣b)2=a2﹣b2 B.(a﹣b)2=a2﹣2ab+b2
C.(a+b)2=a2+2ab+b2 D.a2﹣b2=(a+b)(a﹣b)
7.如图,M是AG的中点,B是AG上一点.分别以AB、BG为边,作正方形ABCD和正方形BGFE,连接MD和MF.设AB=a,BG=b,且a+b=10,ab=21,则图中阴影部分的面积为( )
A.46 B.33 C.28 D.52
8.若x满足(x﹣2021)(2022﹣x)=0.25,则(x﹣2021)2+(2022﹣x)2=( )
A.0.25 B.0.5 C.1 D.﹣0.25
二.填空题(共10小题,满分40分)
9.计算:(﹣m+n)(﹣m﹣n)= .
10.一个正方形的边长增加了3cm,面积相应增加了39cm2,则原来这个正方形的边长为 cm.
11.若a(a﹣1)﹣(a2﹣b)=4,则的值是 .
12.若x2+(m﹣3)x+9是完全平方式,则m= .
13.如图是一个正方形,分成四部分,其面积分别为a2,ab,ab,b2,则原正方形的边长是 .
14.(1)已知x+y=4,xy=3,则x2+y2的值为 .
(2)已知(x+y)2=25,x2+y2=17,则(x﹣y)2的值为 .
(3)已知x满足(x﹣2020)2+(2022﹣x)2=12,则(x﹣2021)2的值为 .
15.若(x+9y)2=(x﹣9y)2+A,则代数式A为 .
16.若2a﹣b=2,则4a2﹣b2﹣4b的值是 .
17.边长为a的正方形ABCD与边长为b的正方形DEFG按如图所示的方式摆放,点A,D,G在同一直线上.已知a+b=10,ab=24.则图中阴影部分的面积为 .
18.计算:(2b﹣3c+4)(3c﹣2b+4)﹣2(b﹣c)2= .
三.解答题(共7小题,满分48分)
19.计算:(9x﹣2y)(x+y)﹣(﹣3x+y)(﹣3x﹣y).
20.(﹣2y+1)2﹣(2y+1)(2y﹣1).
21.要求:利用乘法公式计算.
(1)2023×2021﹣20222;
(2)(2x﹣y+3)(2x﹣y﹣3).
22.若x、y满足x2+y2=,xy=﹣,求下列各式的值.
(1)(x+y)2
(2)x4+y4.
23.阅读例题的解答过程,并解答下列各题.
例:用简便方法计算103×97.
解:103×97=(100+3)(100﹣3)①=1002﹣32②=9991.
(1)例题求解过程中,第②步变形的依据是 ;
(2)用简便方法计算9×11×101;
(3)用简便方法计算20212﹣2020×2022.
24.在课后服务课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b,宽为α的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
【发现】
(1)根据图2,写出一个我们熟悉的数学公式 .
【应用】
(2)根据(1)中的数学公式,解决如下问题:
①已知:a+b=7,a2+b2=25,求ab的值.
②如果一个长方形的长和宽分别为(8﹣x)和(x﹣2),且(8﹣x)2+(x﹣2)2=20,求这个长方形的面积.
25.若x满足(9﹣x)(x﹣4)=4,求(4﹣x)2+(x﹣9)2的值.
解:设9﹣x=a,x﹣4=b,则(9﹣x)(x﹣4)=ab=4,a+b=(9﹣x)+(x﹣4)=5,
∴(9﹣x)2+(x﹣4)2=a2+b2﹣2ab=52﹣2×4=17.
请仿照上面的方法求解下面问题:
(1)若x满足(5﹣x)(x﹣2)=2,求(5﹣x)2+(x﹣2)2的值.
(2)若x满足(6﹣x)(3﹣x)=1,求代数式(9﹣2x)2的值.
(3)已知正方形ABCD的边长为x,E,F分别是AD、DC上的点,且AE=3,CF=5,长方形EMFD的面积是48,分别以MF、DF作正方形,求阴影部分的面积.
参考答案
一.选择题(共8小题,满分32分)
1.解:∵(3x±2)2=9x2±12x+4,
∴b=±12,
故选:D.
2.解:x2+y2
=(x+y)2﹣2xy
=(﹣6)2﹣2×8
=20,
故选:C.
3.解:∵(x±4)2=x2±8x+16,
∴﹣2m=±8,
∴m=±4,
故选:C.
4.解:M===﹣b2﹣3a,
故选:D.
5.解:∵(a+b)2=28,(a﹣b)2=12,
∴a2+b2+2ab=28①,a2+b2﹣2ab=12②,
∴①+②得:
2(a2+b2)=40,
∴a2+b2=20,
故选:C.
6.解:∵图形中阴影部分的面积可表示为a2﹣b2或=(a+b)(a﹣b),
∴a2﹣b2=(a+b)(a﹣b),
故选:D.
7.解:∵(a+b)2=a2+2ab+b2,
∴a2+b2=(a+b)2﹣2ab,
由题意得,图中阴影部分的面积为:
a2+b2﹣(+)
=(a+b)2﹣2ab﹣,
=﹣2ab,
∴当a+b=10,ab=21时,
原式=﹣2×21
=75﹣42
=33,
故选:B.
8.解:(x﹣2021)2+(2022﹣x)2
=(x﹣2021+2022﹣x)2﹣2(x﹣2021)(2022﹣x)
=1﹣2×0.25
=0.5,
故选:B.
二.填空题(共10小题,满分40分)
9.解:原式=(﹣m)2﹣n2
=(m)2﹣n2,
=m2﹣n2
故答案为:m2﹣n2.
10.解:设原来正方形的边长是xcm.根据题意得:
(x+3)2﹣x2=39,
∴(x+3+x)(x+3﹣x)=3(2x+3)=39,
解得x=5.
11.解:∵a(a﹣1)﹣(a2﹣b)=4,
∴a2﹣a﹣a2+b=4,
∴b﹣a=4,
∴====8.
故答案为:8.
12.解:∵x2+(m﹣3)x+9是完全平方式,
∴m﹣3=±6,
解得:m=9或﹣3.
故答案为:9或﹣3.
13.解:原正方形的面积为a2+2ab+b2=(a+b)2,
所以原正方形的边长是a+b,
故答案为:a+b.
14.解:(1)∵x+y=4,xy=3,
∴x2+y2=(x+y)2﹣2xy=16﹣6=10.
故答案为:10;
(2)∵(x+y)2=25,x2+y2=17,
∴x2+y2+2xy﹣(x2+y2)=8,
∴xy=4,
∴(x﹣y)2=x2+y2﹣2xy=17﹣8=9.
故答案为:9;
(3)∵(x﹣2020)2+(x﹣2022)2=12,
∴[(x﹣2021)+1]2+[(x﹣2021)﹣1]2=12,
∴(x﹣2021)2+2(x﹣2021)+1+(x﹣2021)2﹣2(x﹣2021)+1=12,
∴(x﹣2021)2=5.
故答案为:5.
15.解:因为(x+9y)2=x2+18xy+81y2,(x﹣9y)2=x2﹣18xy+81y2,
所以(x+9y)2=x2﹣18xy+81y2+36xy=(x﹣9y)2+36xy,
因为(x+9y)2=(x﹣9y)2+A,
所以A=36xy.
故答案为:36xy.
16.解:∵2a﹣b=2,
∴原式=(2a﹣b)(2a+b)﹣4b=2(2a+b)﹣4b
=4a+2b﹣4b
=4a﹣2b
=2(2a﹣b)
=2×2
=4.
故答案为:4.
17.解:由S阴影部分=S正方形ABCD+S正方形DEFG﹣S△ABC﹣S△AFG可得,
S阴影部分=a2+b2﹣a2﹣b(a+b)
=a2+b2﹣ab
=(a2+b2﹣ab)
=[(a+b)2﹣3ab]
=×(100﹣72)
=14,
故答案为:14.
18.解:(2b﹣3c+4)(3c﹣2b+4)﹣2(b﹣c)2,
=[(2b﹣3c)+4][﹣(2b﹣3c)+4]﹣2(b﹣c)2,
=16﹣(2b﹣3c)2﹣2(b﹣c)2,
=16﹣4b2+12bc﹣9c2﹣2b2+4bc﹣2c2,
=﹣6b2﹣11c2+16bc+16.
三.解答题(共7小题,满分48分)
19.解:(9x﹣2y)(x+y)﹣(﹣3x+y)(﹣3x﹣y)
=9x2+9xy﹣2xy﹣2y2﹣(9x2﹣y2)
=9x2+9xy﹣2xy﹣2y2﹣9x2+y2
=7xy﹣y2.
20.解:原式=4y2﹣4y+1﹣(4y2﹣1)
=4y2﹣4y+1﹣4y2+1
=﹣4y+2.
21.解:(1)原式=(2022+1)×(2022﹣1)﹣20222
=20222﹣1﹣20222
=﹣1.
(2)原式=(2x﹣y)2﹣9
=4x2﹣4xy+y2﹣9.
22.解:(1)∵x2+y2=,xy=﹣,
∴原式=x2+y2+2xy=﹣1=;
(2)∵x2+y2=,xy=﹣,
∴原式=(x2+y2)2﹣2x2y2=﹣=.
23.解:(1)平方差公式;
(2)9×11×101
=(10﹣1)×(10+1)×101
=(100﹣1)×101
=(100﹣1)(100+1)
=1002﹣12
=9999;
(3)20212﹣2020×2022
=20212﹣(2021﹣1)(2021+1)
=20212﹣(20212﹣12)
=20212﹣20212+1
=1.
24.解:(1)由图2可知,(a+b)2=a2+2ab+b2,
故答案为:(a+b)2=a2+2ab+b2;
(2)①∵a+b=7,
∴(a+b)2=a2+2ab+b2=49,
∵a2+b2=25,
∴2ab=24,
∴ab=12;
②由(1)知,[(8﹣x)+(x﹣2)]2=(8﹣x)2+2(8﹣x)(x﹣2)+(x﹣2)2=36,
∵(8﹣x)2+(x﹣2)2=20,
∴2(8﹣x)(x﹣2)=16,
∴(8﹣x)(x﹣2)=8,
故这个长方形的面积为8.
25.解:(1)设(5﹣x)=a,(x﹣2)=b,
则(5﹣x)(x﹣2)=ab=2,
a+b=(5﹣x)+(x﹣2)=3,
∴(5﹣x)2+(x﹣2)2
=(a+b)2﹣2ab
=32﹣2×2
=5;
(2)设(6﹣x)=a,(3﹣x)=b,
(6﹣x)(3﹣x)=ab=1,
a﹣b=(6﹣x)﹣(3﹣x)=3,
∵(a+b)2
=(a﹣b)2+4ab
=13,
∴(a+b)2=13,
∵(6﹣x)+(3﹣x)=a+b,
∴9﹣2x=a+b,
∴(9﹣2x)2=(a+b)2=13.
(3)∵正方形ABCD的边长为x,AE=3,CF=5,
∴MF=DE=x﹣3,DF=x﹣5,
∴(x﹣3) (x﹣5)=48,
∴(x﹣3)﹣(x﹣5)=2,
∴阴影部分的面积=FM2﹣DF2=(x﹣3)2﹣(x﹣5)2.
设(x﹣3)=a,(x﹣5)=b,则(x﹣3)(x﹣5)=ab=48,
a﹣b=(x﹣3)﹣(x﹣5)=2,
∴a=8,b=6,a+b=14,
∴(x﹣3)2﹣(x﹣5)2=a2﹣b2=(a+b)(a﹣b)=14×2=28.
即阴影部分的面积是28.
