6.3反比例函数的应用 同步复习小测 2022-2023学年北师大版九年级数学上册(Word版含答案)
文档属性
| 名称 | 6.3反比例函数的应用 同步复习小测 2022-2023学年北师大版九年级数学上册(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 182.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-11 00:00:00 | ||
图片预览


文档简介
6.3反比例函数的应用---九年级同步复习小测(基础复习+能力提升)
【北师大版】
【基础复习】
一、单选题
1.矩形面积为4,它的长y与宽x之间的函数关系用图象大致可表示为( )
A. B.
C. D.
2.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.则用电阻R表示电流I的函数表达式为( )
A. B. C. D.
3.在平面直角坐标系中,已知△ABC为等腰直角三角形,CB=CA=5,点C(0,3),点B在x轴正半轴上,点A在第三象限,且在反比例函数y= 的图象上,则k=( )
A.3 B.4 C.6 D.12
4.已知点A(﹣2,1),B(1,4),若反比例函数y= 与线段AB有公共点时,k的取值范围是( )
A.﹣2≤k≤4 B.k≤﹣2或k≥4
C.﹣2≤k<0或k≥4 D.﹣2≤k<0或0<k≤4
5.在平面直角坐标系xOy中,第一象限内的点P在反比例函数的图象上,如果点P的纵坐标是3,OP=5,那么该函数的表达式为( )
A. y= B. y=- C. y= D. y=-
6.如图,反比例函数y1=和正比例函数y2=k2x的图象交于A(-1,-3)、B(1,3)两点,若>k2x,则x的取值范围是( )
A.-1<x<0 B.-1<x<1
C.x<-1或0<x<1 D.-1<x<0或x>1
二、填空题
7.反比例函数y= 的图象经过点(﹣2,3),则k的值为 .
8.如图、正比例函数 与反比例函数 的图象交于(1,2),则在第一象限内不等式 的解集为 .
9.如图,已知直线l:y=﹣x,双曲线y= ,在l上取一点A(a,﹣a)(a>0),过A作x轴的垂线交双曲线于点B,过B作y轴的垂线交l于点C,过C作x轴的垂线交双曲线于点D,过D作y轴的垂线交l于点E,此时E与A重合,并得到一个正方形ABCD,若原点O在正方形ABCD的对角线上且分这条对角线为1:2的两条线段,则a的值为 .
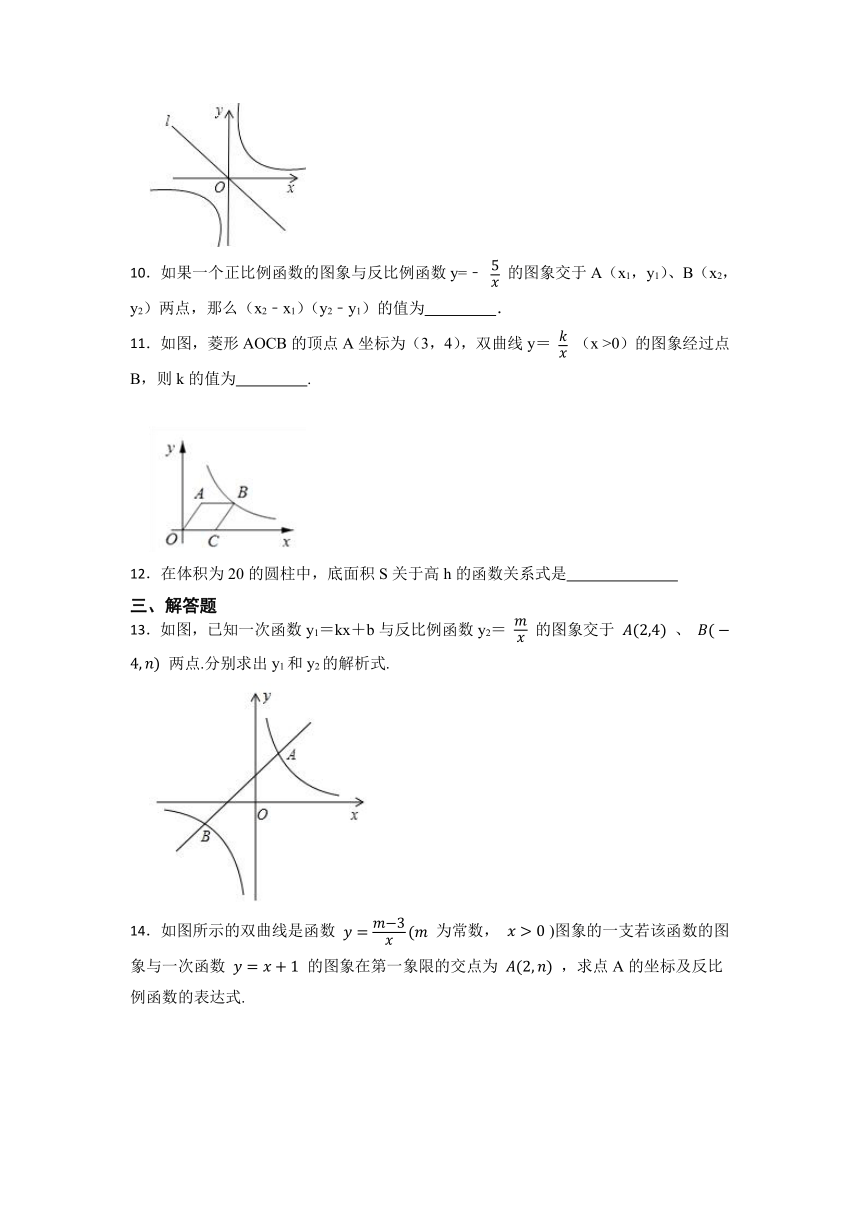
10.如果一个正比例函数的图象与反比例函数y=﹣ 的图象交于A(x1,y1)、B(x2,y2)两点,那么(x2﹣x1)(y2﹣y1)的值为 .
11.如图,菱形AOCB的顶点A坐标为(3,4),双曲线y= (x >0)的图象经过点B,则k的值为 .
12.在体积为20的圆柱中,底面积S关于高h的函数关系式是
三、解答题
13.如图,已知一次函数y1=kx+b与反比例函数y2= 的图象交于 、 两点.分别求出y1和y2的解析式.
14.如图所示的双曲线是函数 为常数, )图象的一支若该函数的图象与一次函数 的图象在第一象限的交点为 ,求点A的坐标及反比例函数的表达式.
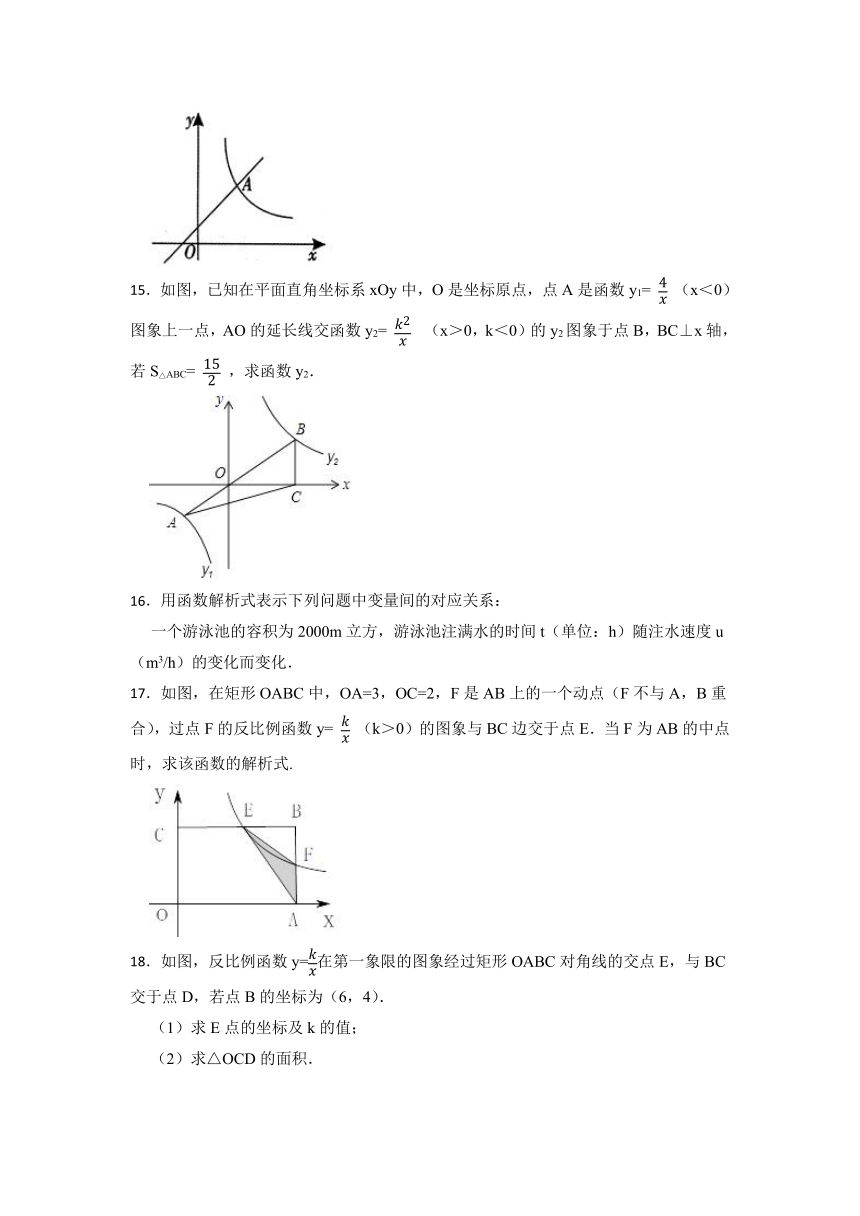
15.如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y1= (x<0)图象上一点,AO的延长线交函数y2= (x>0,k<0)的y2图象于点B,BC⊥x轴,若S△ABC= ,求函数y2.
16.用函数解析式表示下列问题中变量间的对应关系:
一个游泳池的容积为2000m立方,游泳池注满水的时间t(单位:h)随注水速度u(m3/h)的变化而变化.
17.如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y= (k>0)的图象与BC边交于点E.当F为AB的中点时,求该函数的解析式.
18.如图,反比例函数y=在第一象限的图象经过矩形OABC对角线的交点E,与BC交于点D,若点B的坐标为(6,4).
(1)求E点的坐标及k的值;
(2)求△OCD的面积.
【能力提升】
一、单选题
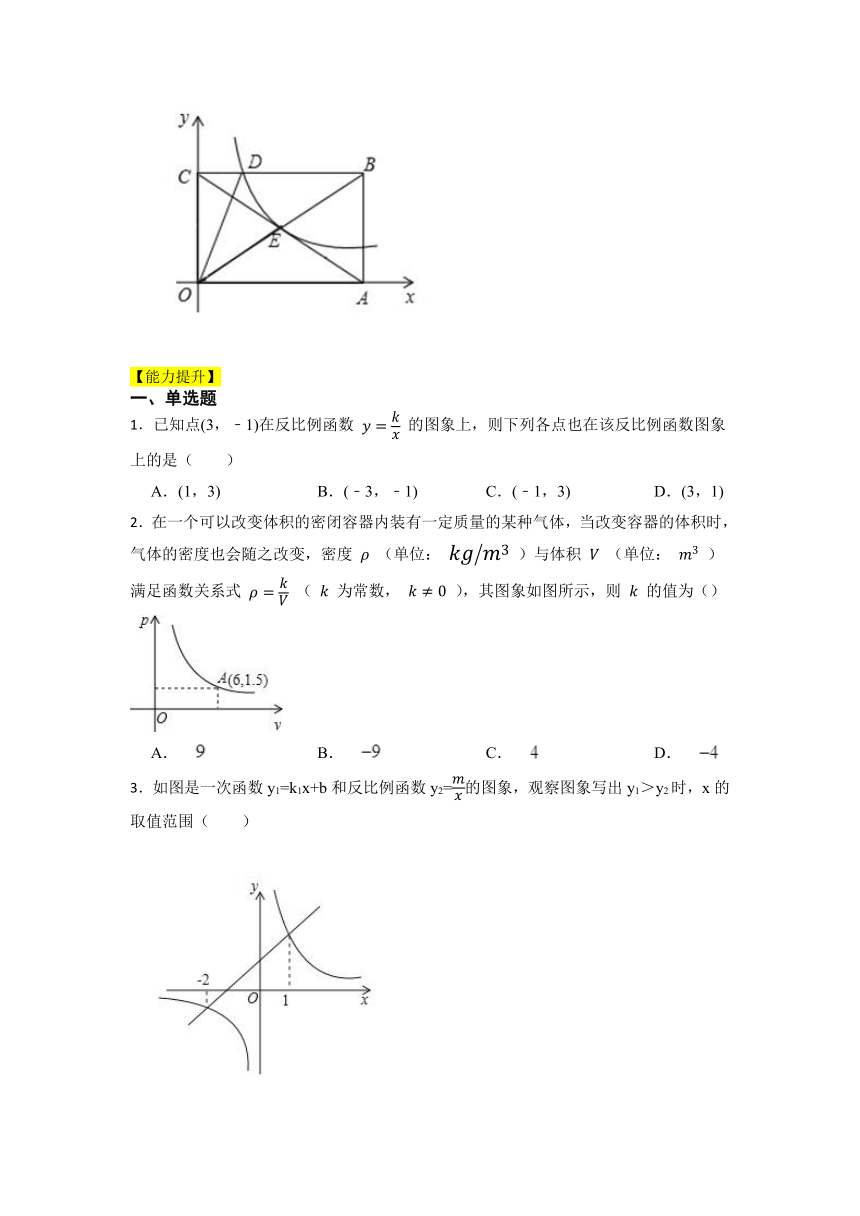
1.已知点(3,﹣1)在反比例函数 的图象上,则下列各点也在该反比例函数图象上的是( )
A.(1,3) B.(﹣3,﹣1) C.(﹣1,3) D.(3,1)
2.在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也会随之改变,密度 (单位: )与体积 (单位: )满足函数关系式 ( 为常数, ),其图象如图所示,则 的值为()
A. B. C. D.
3.如图是一次函数y1=k1x+b和反比例函数y2=的图象,观察图象写出y1>y2时,x的取值范围( )
A.-2<x<0或x>1 B.-2<x<1
C.x<-2或x>1 D.x<-2或0<x<1
4.若反比例函数 的图象经过点(1,4),则此反比例函数图象经过( )
A.第一、三象限 B.第一、二象限
C.第二、四象限 D.第三、四象限
5.已知点A(-1,5)在反比例函数y=的图象上,则该函数的解析式为( )
A.y= B.y= C.y=- D.y=5x
6.反比例函数y= 的图象与直线y=﹣x+2有两个交点,且两交点横坐标的积为负数,则t的取值范围是( )
A.t< B.t> C.t≤ D.t≥
二、填空题
7.近视眼镜的度数y(度)与镜片焦距x(m)成反比例,已知400度近视眼镜镜片的焦距为0.25m,则眼镜度数与镜片焦距之间的函数关系式为 .
8.在平面直角坐标系中,正比例函数y=3x与反比例函数y= 的图象交于点A(a,﹣6),则k= .
9.反比例函数 的图像经过点(2,3),则 的值等于 .
10.如图,一次函数y=kx+b的图象与反比例函数 的图象交于A(﹣2,1)、B(1,﹣2)两点.一次函数的值大于反比例函数的值时x的取值范围是 .
11.一司机驾驶汽车从甲地去乙地,他以80千米/小时的平均速度用了4小时到达乙地,当他按照原路返回时,汽车的速度v千米/小时与时间t小时的函数关系式是 .
12.一批零件300个,一个工人每小时做15个,用关系式表示人数x与完成任务所需的时间y之间的函数关系式为 .
三、解答题
13.已知:如图,在平面直角坐标系xoy中,直线 与x轴交于点A,与双曲线 在第一象限内交于点B,BC垂直x轴于点C,OC=2AO.求双曲线 的解析式.
14.如图,已知A(﹣2,﹣2)、B(n,4)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积.
15.如图,已知A(﹣4,n),B(1,﹣4)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)求不等式kx+b﹣<0的解集(请直接写出答案).
16.已知圆锥的体积,(其中s表示圆锥的底面积,h表示圆锥的高).若圆锥的体积不变,当h为10cm时,底面积为30cm2,请写出h关于s的函数解析式.
【基础复习答案】
1.【答案】B
【解析】【解答】由矩形的面积4=xy,可知y与x间的关系式为y= (x>0),是反比例函数图象,且其图象在第一象限.
故答案为:B.
【分析】根据矩形的面积公式得矩形的面积4=xy (x>0),根据两个变量的乘积是一个定值得出y与x成反比例函数关系,根据反比例函数的图象是双曲线,又自变量的取值是正数,故图像的一支在第一象限,从而做出选择。
2.【答案】D
【解析】【解答】由题意可设 ,
∵该函数的图象过点(2,3),
∴ ,
∴该函数的表达式为: .
【分析】因为双曲线过点(2,3),所以可用待定系数法求解析式。
3.【答案】A
【解析】【解答】如图,作AH⊥y轴于H.
∵CA=CB,∠AHC=∠BOC,∠ACH=∠CBO,
∴△ACH≌△CBO,
∴AH=OC,CH=OB,
∵C(0,3),BC=5,
∴OC=3,OB= =4,
∴CH=OB=4,AH=OC=3,
∴OH=1,
∴A(-3,-1),
∵点A在y= 上,
∴k=3,
故答案为:A.
【分析】如图,作AH⊥y轴于H.根据同角的余角相等得出∠ACH=∠CBO,然后由AAS判断出△ACH≌△CBO,根据全等三角形的对应边相等得出AH=OC,CH=OB,从而得出A点的坐标,再将A点的坐标代入双曲线的解集线即可求出k的值。
4.【答案】D
【解析】【解答】解:①当k>0时,如下图:
将x=1代入反比例函数的解析式得y=k,
∵y随x的增大而减小,
∴当k≤4时,反比例函数y= 与线段AB有公共点.
∴当0<k≤4时,反比例函数y= 与线段AB有公共点.
②当k<0时,如下图所示:
将x=﹣2代入反比例函数得解析式得:y=﹣ ,
∵反比例函数得图象随着x得增大而增大,
∴当﹣ ≤1时,反比例函数y= 与线段AB有公共点.
解得:k≥﹣2,
∴﹣2≤k<0.
综上所述,当﹣2≤k<0或0<k≤4时,反比例函数y= 与线段AB有公共点.
故选;D.
【分析】当k>0时,将x=1代入反比例函数的解析式的y=k,当k≤4时,反比例函数y= 与线段AB有公共点;当k<0时,将x=﹣2代入反比例函数的解析式得:y= ,当 时,反比例函数图象与线段AB有公共点.
5.【答案】A
【解析】【解答】解:在RT△OPD中,过P作PD⊥x轴于D,则PD=3,
∴OD= =4,
∴P(4,3),
∴代入反比例函数y=得,3=,
解得k=12,
∴反比例函数的解析式为y=,
故选A.
【分析】过P作PD⊥x轴于D,则PD=3,根据勾股定理求得OD,得出D的坐标,然后根据待定系数法即可求得反比例函数的解析式.
6.【答案】C
【解析】【解答】由图可知,在A点左侧,反比例函数的值大于一次函数的值,此时x<-1;
在B点左侧,y轴的右侧,反比例函数的值大于一次函数的值,此时0<x<1.
故选C.
【分析】根据图象的交点坐标及函数的大小关系,直接解答.要充分利用函数图象所给的信息解答.本题考查了反比例函数与一次函数的交点问题,将关于算式的问题转化为图象问题是解题的关键.
7.【答案】-6
【解析】【解答】把( 2,3)代入函数y= 中,得3= ,解得k= 6.
故答案为: 6.
【分析】根据题意把点(-2,3)代入反比例函数的解析式计算即可求解。
8.【答案】x>1
【解析】【解答】解:根据图象可得:第一象限内不等式k1x>
的解集为x>1.
故答案是:x>1.
【分析】在第一象限内不等式k1x> 的解集就是正比例函数图象都在反比例函数图象上方时x的取值范围.
9.【答案】或
【解析】【解答】解:依照题意画出图形,如图所示.
∵点A的坐标为(a,﹣a)(a>0),
∴点B(a, )、点C(﹣ , )、点D(﹣ ,﹣a),
∴OA= = a,OC= = .
又∵原点O分对角线AC为1:2的两条线段,
∴OA=2OC或OC=2OA,
即 a=2× 或 =2 a,
解得:a1= ,a2=﹣ (舍去),a3= ,a4=﹣ (舍去).
故答案为: 或 .
【分析】本题属于基础题,难度不大,解决该题型题目时,找出点的坐标,再由两点间的距离公式求出线段的长度是关键.根据点的选取方法找出点B、C、D的坐标,由两点间的距离公式表示出线段OA、OC的长,再根据两线段的关系可得出关于a的一元二次方程,解方程即可得出结论.本题考查了反比例函数与一次函数的交点问题、两点间的距离公式以及解一元二次方程,解题的关键是找出线段OA、OC的长.
10.【答案】﹣20
【解析】【解答】解:∵正比例函数的图象与反比例函数y=﹣ 的图象交于A(x1,y1)、B(x2,y2)两点,关于原点对称,依此可得x1=﹣x2,y1=﹣y2,
∴(x2﹣x1)(y2﹣y1)
=x2y2﹣x2y1﹣x1y2+x1y1
=x2y2+x2y2+x1y1+x1y1
=﹣5×4
=﹣20.
故答案为:﹣20.
【分析】正比例函数的图象与反比例函数y=﹣ 的两交点坐标关于原点对称,依此可得x1=﹣x2,y1=﹣y2,将(x2﹣x1)(y2﹣y1)展开,依此关系即可求解.
11.【答案】32
【解析】【解答】过A作AM⊥x轴于M,过B作BN⊥x轴于N,
则∠AMO=∠BNC=90°,
∵四边形AOCB是菱形,
∴OA=BC=AB=OC,AB∥OC,OA∥BC,
∴∠AOM=∠BCN,
∵A(3,4),
∴OM=3,AM=4,由勾股定理得:OA=5,
即OC=OA=AB=BC=5,
在△AOM和△BCN中 ,
∴△AOM≌△BCN(AAS),
∴BN=AM=4,CN=OM=3,
∴ON=5+3=8,
即B点的坐标是(8,4),
把B的坐标代入y= ,
得:k=32,
故答案为:32.
【分析】过A作AM⊥x轴于M,过B作BN⊥x轴于N,根据菱形的性质及点A的坐标,可求出OA的长,再证明△AOM≌△BCN,得出BN、ON的长,就可求得点B的坐标,利用待定系数法,可求出反比例函数的解析式。
12.【答案】s=.
【解析】【解答】解:由题意得:底面积S关于高h的函数关系式是s=.
故本题答案为:s=.
【分析】根据等量关系“圆柱底面积=圆柱体积÷圆柱高”即可列出关系式.
13.【答案】解:把点 代入
当 时,
把 , 代入y1=kx+b
,
①-②得,
把 代入①得,
即
.
【解析】【分析】先把A点坐标代入 y2= ,求出反比例函数解析式,接着把 代入反比例函数求出B点坐标,最后把A、B两点坐标代入一次函数 y1=kx+b ,解出k、b即可得到一次函数解析式.
14.【答案】解: 点 在一次函数 的图象上,
点A的坐标为 .
又 点A在反比例函数 为常数, )的图象上,
反比例函数的表达式为 .
【解析】【分析】先将x=2代入一次函数 中可得,点A的坐标为 ,再将点A的坐标代入 可得反比例函数的解析式.
15.【答案】解:设A(m, )(m<0),
直线AB的解析式为y=ax(k≠0),
∵A(m, ),
∴ma= ,解得a= ,
∴直线AB的解析式为y= x.
∵AO的延长线交函数y= 的图象于点B,
∴B(﹣ mk,﹣ ),
∵△ABC的面积等于 ,CB⊥x轴,
∴ ×(﹣ )×(﹣ mk+|m|)= ,解得k1=﹣5(舍去),k2=3,
∴y2=
【解析】【分析】设A(m, )(m<0),则可得到直线AB的解析式为y= x.再利用反比例函数与一次函数的交点问题可表示出B(﹣ mk,﹣ ),则利用三角形面积公式得到 ×(﹣ )×(﹣ mk+|m|)= ,解得k1=﹣5(舍去),k2=3,于是得到y2= .
16.【答案】解:由题意得ut=2000,
整理得t=.
【解析】【分析】根据注水速度×注水时间=游泳池的容积可得ut=2000,变形即可求出t与u的函数解析式.
17.【答案】解:∵在矩形OABC中,OA=3,OC=2,∴B(3,2).∵F为AB的中点,∴F(3,1).∵点F在反比例函数 (k>0)的图象上,∴k=3,∴该函数的解析式为 (x>0)
【解析】【分析】根据矩形的性质由矩形的边长OA=3,OC=2得出B点的坐标,又F为AB的中点,故能得出F点的坐标,然后将F点的坐标代入反比例函数的解析式,即可求出比例系数K的值,从而得出反比例函数的解析式。
18.【答案】解:(1)∵E是矩形OABC对角线的交点,
∴OE=EB,
∵点B的坐标为(6,4),
∴E点的坐标是(3,2),
把x=3,y=2代入y=得k=6;
(2)设点D的坐标为(x,y),则S△OCD=OC×OD,
即S△OCD=xy=k,
由(1)知k=6,
∴S△OCD=k=3.
【解析】【分析】(1)由E是矩形OABC对角线的交点,得到OE=EB,由于点B的坐标为(6,4),于是得到E点的坐标是(3,2),即可得到结论;
(2)设点D的坐标为(x,y),即S△OCD=xy=k=3.
【能力提升答案】
1.【答案】C
【解析】【解答】解:∵点(3,﹣1)在反比例函数 的图象上,
∴k=3×(﹣1)=﹣3,
而1×3=﹣3×(﹣1)=3×1=3,﹣1×3=﹣3,
∴点(﹣1,3)在该反比例函数图象上.
故答案为:C.
【分析】先求出k=3×(﹣1)=﹣3,再求解即可。
2.【答案】A
【解析】【解答】解:如图:
由图象可知,函数图象经过点(6,1.5),
设反比例函数为 ,
则1.5= ,
解得k=9,
故答案为:A.
【分析】由题意可知图像过点(6,1.5),把这个点代入计算即可求解。
3.【答案】A
【解析】【分析】根据图象可以知道一次函数y1=k1x+b和反比例函数y2=(k1 k2≠0)的图象的交点的横坐标,若y1>y2,则根据图象可以确定x的取值范围.
【解答】如图,依题意得一次函数y1=k1x+b和反比例函数y2=(k1 k2≠0)的图象的交点的横坐标分别为x=-2或x=1,
若y1>y2,则y1的图象在y2的上面,
x的取值范围是-2<x<0或x>1.
故选A.
【点评】此题主要考查了反比例函数与一次函数的图象的交点问题,解题的关键是利用数形结合的方法解决问题.
4.【答案】A
【解析】【解答】解:∵反比例函数 的图象经过点 ,
∴ ,
即 ,
∴反比例函数的图象经过第一、三象限.
故答案为:A.
【分析】利用待定系数法求出k的值,可得到函数解析式,再利用反比例函数的图象与系数的关系可得答案.
5.【答案】C
【解析】【分析】设出反比例函数解析式,将P(-1,5)代入解析式求出k的值即可.
【解答】将P(-1,5)代入解析式y=得,
k=(-1)×5=-5,
解析式为:y=-.
故选C.
【点评】解答此题要明确待定系数法:现设某些未知的系数,然后根据已知条件求出未知系数的方法叫待定系数法.
6.【答案】B
【解析】【解答】由题意可得:﹣x+2= ,
所以x2﹣2x+1﹣6t=0,
∵两函数图象有两个交点,且两交点横坐标的积为负数,
∴
解不等式组,得t> .
故答案为:B.
【分析】联立函数解析式整理得到关于x的一元二次方程,则方程有两个不相等的实数根,即△>0,又由于横坐标的积为负数,则两个解的积为负数,根据根与系数关系可得关于t的不等式,联立求解可得t的范围.
7.【答案】y=
【解析】【解答】解:设该反比例函数的解析式为
将x= ,y=400代入,得
解得:k=100
∴眼镜度数与镜片焦距之间的函数关系式为
故答案为: .
【分析】设该反比例函数的解析式为 ,然后将x= ,y=400代入即可求出函数关系式.
8.【答案】12
【解析】【解答】解:∵点A(a,﹣6)在正比例函数y=3x的图象上,
∴﹣6=3a,
解得a=﹣2,
∴A(﹣2,﹣6)
∵点A(﹣2,﹣6)在反比例函数y= 的图象上,
∴k=﹣2×(﹣6)=12,
故答案为:12.
【分析】先根据y=3x求得A的坐标,再把点A的坐标代入反比例函数的解析式即可求出k的值.
9.【答案】8
【解析】【解答】解:∵反比例函数经过点(2,3)
∴k-2=2×3=6
解之:k=8
故答案为:8
【分析】把点(2,3)代入已知函数解析式,列出关于k的方程,通过解方程即可求得k的值。
10.【答案】x<﹣2或0<x<1
【解析】【解答】解:∵A(﹣2,1),B(1,﹣2),
由图象可知:一次函数的值大于反比例函数的值时x的取值范围是x<﹣2或0<x<1.
故答案为:x<﹣2或0<x<1.
【分析】根据两函数的交点坐标可知要使一次函数的值大于反比例函数的值,就要观察直线x=-2,x=0,x=1将两函数的图象分成四部分,观察函数图象可得出x的取值范围。
11.【答案】v=
【解析】【解答】解:∵一司机驾驶汽车从甲地去乙地,他以80千米/时的平均速度用了4小时到达乙地,那么路程为80×4=320千米,
∴汽车的速度v(千米/小时)与时间t(小时)的函数关系为v= .
故答案为v= .
【分析】先求得路程,再由等量关系“速度=路程÷时间”列出关系式即可.
12.【答案】
【解析】【解答】解:由题意得:人数x与完成任务所需的时间y之间的函数关系式为y=300÷15x=.
故本题答案为:y=.
【分析】根据等量关系“x个工人所需时间=工作总量÷x个工人工效”即可列出关系式.
13.【答案】解:在 中,令y=0,得 .解得 .∴直线 与x轴的交点A的坐标为:(-1,0)∴AO=1.∵OC=2AO,∴OC=2.∵BC⊥x轴于点C,∴点B的横坐标为2.∵点B在直线 上,∴ .∴点B的坐标为 .∵双曲线 过点B ,∴ .解得 .∴双曲线的解析式为
【解析】【分析】利用一次函数的值为0求出对应的x的值,就可得出点A的坐标,再根据OC=2OA,可得出OC的长,从而可得出点B的横坐标,将点B的横坐标代入一次函数解析式求出点B的纵坐标,即可得出点B的坐标,然后利用待定系数法,由点B的坐标就可求出双曲线的解析式。
14.【答案】解:(1)∵A(﹣2,﹣2)在y=上,∴m=4.∴反比例函数的解析式为y=.∵点B(n,4)在y=上,∴n=1.∴B(1,4).∵y=kx+b经过A(﹣2,﹣2),B(1,4),∴.解之得.∴一次函数的解析式为y=2x+2.(2)设C是直线AB与y轴的交点,∴当x=0时,y=2.∴点C(0,2).∴OC=2.∴S△AOB=S△ACO+S△BCO=×2×2+×2×1=3.
【解析】【分析】(1)把A(﹣2,﹣2)代入反比例函数y=,得出m的值,再把B(n,4)代入一次函数的解析式y=kx+b,运用待定系数法分别求其解析式;
(2)设直线AB与y轴交于点C,把三角形AOB的面积看成是三角形AOC和三角形OCB的面积之和进行计算.
15.【答案】解:(1)∵反比例函数y=(m≠0)过点B(1,﹣4),∴m=1×(﹣4)=﹣4,∴y=﹣,将x=﹣4,y=n代入反比例解析式得:n=1,∴A(﹣4,1),∴将A与B坐标代入一次函数解析式得:,解得:,∴y=﹣x﹣3;(2)在直线y=﹣x﹣3中,当y=0时,x=﹣3,∴C(﹣3,0),即OC=3,∴S△AOB=S△AOC+S△COB=(3×1+3×4)=;(3)不等式kx+b﹣<0的解集是﹣4<x<0或x>1.
【解析】【分析】(1)将B坐标代入反比例解析式中求出m的值,即可确定出反比例解析式;将A坐标代入反比例解析式求出n的值,确定出A的坐标,将A与B坐标代入一次函数解析式中求出k与b的值,即可确定出一次函数解析式;
(2)对于直线AB,令y=0求出x的值,即可确定出C坐标,三角形AOB面积=三角形AOC面积+三角形BOC面积,求出即可;
(3)由两函数交点A与B的横坐标,利用图象即可求出所求不等式的解集.
16.【答案】解:∵,当h为10cm时,底面积为30,
∴V=×10×30=100(cm3),
∴100=sh,
∴h关于s的函数解析式为:.
【解析】【分析】首先根据已知求出V的值,进而代入,即可得出h与s的函数关系式.
【北师大版】
【基础复习】
一、单选题
1.矩形面积为4,它的长y与宽x之间的函数关系用图象大致可表示为( )
A. B.
C. D.
2.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.则用电阻R表示电流I的函数表达式为( )
A. B. C. D.
3.在平面直角坐标系中,已知△ABC为等腰直角三角形,CB=CA=5,点C(0,3),点B在x轴正半轴上,点A在第三象限,且在反比例函数y= 的图象上,则k=( )
A.3 B.4 C.6 D.12
4.已知点A(﹣2,1),B(1,4),若反比例函数y= 与线段AB有公共点时,k的取值范围是( )
A.﹣2≤k≤4 B.k≤﹣2或k≥4
C.﹣2≤k<0或k≥4 D.﹣2≤k<0或0<k≤4
5.在平面直角坐标系xOy中,第一象限内的点P在反比例函数的图象上,如果点P的纵坐标是3,OP=5,那么该函数的表达式为( )
A. y= B. y=- C. y= D. y=-
6.如图,反比例函数y1=和正比例函数y2=k2x的图象交于A(-1,-3)、B(1,3)两点,若>k2x,则x的取值范围是( )
A.-1<x<0 B.-1<x<1
C.x<-1或0<x<1 D.-1<x<0或x>1
二、填空题
7.反比例函数y= 的图象经过点(﹣2,3),则k的值为 .
8.如图、正比例函数 与反比例函数 的图象交于(1,2),则在第一象限内不等式 的解集为 .
9.如图,已知直线l:y=﹣x,双曲线y= ,在l上取一点A(a,﹣a)(a>0),过A作x轴的垂线交双曲线于点B,过B作y轴的垂线交l于点C,过C作x轴的垂线交双曲线于点D,过D作y轴的垂线交l于点E,此时E与A重合,并得到一个正方形ABCD,若原点O在正方形ABCD的对角线上且分这条对角线为1:2的两条线段,则a的值为 .
10.如果一个正比例函数的图象与反比例函数y=﹣ 的图象交于A(x1,y1)、B(x2,y2)两点,那么(x2﹣x1)(y2﹣y1)的值为 .
11.如图,菱形AOCB的顶点A坐标为(3,4),双曲线y= (x >0)的图象经过点B,则k的值为 .
12.在体积为20的圆柱中,底面积S关于高h的函数关系式是
三、解答题
13.如图,已知一次函数y1=kx+b与反比例函数y2= 的图象交于 、 两点.分别求出y1和y2的解析式.
14.如图所示的双曲线是函数 为常数, )图象的一支若该函数的图象与一次函数 的图象在第一象限的交点为 ,求点A的坐标及反比例函数的表达式.
15.如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y1= (x<0)图象上一点,AO的延长线交函数y2= (x>0,k<0)的y2图象于点B,BC⊥x轴,若S△ABC= ,求函数y2.
16.用函数解析式表示下列问题中变量间的对应关系:
一个游泳池的容积为2000m立方,游泳池注满水的时间t(单位:h)随注水速度u(m3/h)的变化而变化.
17.如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y= (k>0)的图象与BC边交于点E.当F为AB的中点时,求该函数的解析式.
18.如图,反比例函数y=在第一象限的图象经过矩形OABC对角线的交点E,与BC交于点D,若点B的坐标为(6,4).
(1)求E点的坐标及k的值;
(2)求△OCD的面积.
【能力提升】
一、单选题
1.已知点(3,﹣1)在反比例函数 的图象上,则下列各点也在该反比例函数图象上的是( )
A.(1,3) B.(﹣3,﹣1) C.(﹣1,3) D.(3,1)
2.在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也会随之改变,密度 (单位: )与体积 (单位: )满足函数关系式 ( 为常数, ),其图象如图所示,则 的值为()
A. B. C. D.
3.如图是一次函数y1=k1x+b和反比例函数y2=的图象,观察图象写出y1>y2时,x的取值范围( )
A.-2<x<0或x>1 B.-2<x<1
C.x<-2或x>1 D.x<-2或0<x<1
4.若反比例函数 的图象经过点(1,4),则此反比例函数图象经过( )
A.第一、三象限 B.第一、二象限
C.第二、四象限 D.第三、四象限
5.已知点A(-1,5)在反比例函数y=的图象上,则该函数的解析式为( )
A.y= B.y= C.y=- D.y=5x
6.反比例函数y= 的图象与直线y=﹣x+2有两个交点,且两交点横坐标的积为负数,则t的取值范围是( )
A.t< B.t> C.t≤ D.t≥
二、填空题
7.近视眼镜的度数y(度)与镜片焦距x(m)成反比例,已知400度近视眼镜镜片的焦距为0.25m,则眼镜度数与镜片焦距之间的函数关系式为 .
8.在平面直角坐标系中,正比例函数y=3x与反比例函数y= 的图象交于点A(a,﹣6),则k= .
9.反比例函数 的图像经过点(2,3),则 的值等于 .
10.如图,一次函数y=kx+b的图象与反比例函数 的图象交于A(﹣2,1)、B(1,﹣2)两点.一次函数的值大于反比例函数的值时x的取值范围是 .
11.一司机驾驶汽车从甲地去乙地,他以80千米/小时的平均速度用了4小时到达乙地,当他按照原路返回时,汽车的速度v千米/小时与时间t小时的函数关系式是 .
12.一批零件300个,一个工人每小时做15个,用关系式表示人数x与完成任务所需的时间y之间的函数关系式为 .
三、解答题
13.已知:如图,在平面直角坐标系xoy中,直线 与x轴交于点A,与双曲线 在第一象限内交于点B,BC垂直x轴于点C,OC=2AO.求双曲线 的解析式.
14.如图,已知A(﹣2,﹣2)、B(n,4)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积.
15.如图,已知A(﹣4,n),B(1,﹣4)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)求不等式kx+b﹣<0的解集(请直接写出答案).
16.已知圆锥的体积,(其中s表示圆锥的底面积,h表示圆锥的高).若圆锥的体积不变,当h为10cm时,底面积为30cm2,请写出h关于s的函数解析式.
【基础复习答案】
1.【答案】B
【解析】【解答】由矩形的面积4=xy,可知y与x间的关系式为y= (x>0),是反比例函数图象,且其图象在第一象限.
故答案为:B.
【分析】根据矩形的面积公式得矩形的面积4=xy (x>0),根据两个变量的乘积是一个定值得出y与x成反比例函数关系,根据反比例函数的图象是双曲线,又自变量的取值是正数,故图像的一支在第一象限,从而做出选择。
2.【答案】D
【解析】【解答】由题意可设 ,
∵该函数的图象过点(2,3),
∴ ,
∴该函数的表达式为: .
【分析】因为双曲线过点(2,3),所以可用待定系数法求解析式。
3.【答案】A
【解析】【解答】如图,作AH⊥y轴于H.
∵CA=CB,∠AHC=∠BOC,∠ACH=∠CBO,
∴△ACH≌△CBO,
∴AH=OC,CH=OB,
∵C(0,3),BC=5,
∴OC=3,OB= =4,
∴CH=OB=4,AH=OC=3,
∴OH=1,
∴A(-3,-1),
∵点A在y= 上,
∴k=3,
故答案为:A.
【分析】如图,作AH⊥y轴于H.根据同角的余角相等得出∠ACH=∠CBO,然后由AAS判断出△ACH≌△CBO,根据全等三角形的对应边相等得出AH=OC,CH=OB,从而得出A点的坐标,再将A点的坐标代入双曲线的解集线即可求出k的值。
4.【答案】D
【解析】【解答】解:①当k>0时,如下图:
将x=1代入反比例函数的解析式得y=k,
∵y随x的增大而减小,
∴当k≤4时,反比例函数y= 与线段AB有公共点.
∴当0<k≤4时,反比例函数y= 与线段AB有公共点.
②当k<0时,如下图所示:
将x=﹣2代入反比例函数得解析式得:y=﹣ ,
∵反比例函数得图象随着x得增大而增大,
∴当﹣ ≤1时,反比例函数y= 与线段AB有公共点.
解得:k≥﹣2,
∴﹣2≤k<0.
综上所述,当﹣2≤k<0或0<k≤4时,反比例函数y= 与线段AB有公共点.
故选;D.
【分析】当k>0时,将x=1代入反比例函数的解析式的y=k,当k≤4时,反比例函数y= 与线段AB有公共点;当k<0时,将x=﹣2代入反比例函数的解析式得:y= ,当 时,反比例函数图象与线段AB有公共点.
5.【答案】A
【解析】【解答】解:在RT△OPD中,过P作PD⊥x轴于D,则PD=3,
∴OD= =4,
∴P(4,3),
∴代入反比例函数y=得,3=,
解得k=12,
∴反比例函数的解析式为y=,
故选A.
【分析】过P作PD⊥x轴于D,则PD=3,根据勾股定理求得OD,得出D的坐标,然后根据待定系数法即可求得反比例函数的解析式.
6.【答案】C
【解析】【解答】由图可知,在A点左侧,反比例函数的值大于一次函数的值,此时x<-1;
在B点左侧,y轴的右侧,反比例函数的值大于一次函数的值,此时0<x<1.
故选C.
【分析】根据图象的交点坐标及函数的大小关系,直接解答.要充分利用函数图象所给的信息解答.本题考查了反比例函数与一次函数的交点问题,将关于算式的问题转化为图象问题是解题的关键.
7.【答案】-6
【解析】【解答】把( 2,3)代入函数y= 中,得3= ,解得k= 6.
故答案为: 6.
【分析】根据题意把点(-2,3)代入反比例函数的解析式计算即可求解。
8.【答案】x>1
【解析】【解答】解:根据图象可得:第一象限内不等式k1x>
的解集为x>1.
故答案是:x>1.
【分析】在第一象限内不等式k1x> 的解集就是正比例函数图象都在反比例函数图象上方时x的取值范围.
9.【答案】或
【解析】【解答】解:依照题意画出图形,如图所示.
∵点A的坐标为(a,﹣a)(a>0),
∴点B(a, )、点C(﹣ , )、点D(﹣ ,﹣a),
∴OA= = a,OC= = .
又∵原点O分对角线AC为1:2的两条线段,
∴OA=2OC或OC=2OA,
即 a=2× 或 =2 a,
解得:a1= ,a2=﹣ (舍去),a3= ,a4=﹣ (舍去).
故答案为: 或 .
【分析】本题属于基础题,难度不大,解决该题型题目时,找出点的坐标,再由两点间的距离公式求出线段的长度是关键.根据点的选取方法找出点B、C、D的坐标,由两点间的距离公式表示出线段OA、OC的长,再根据两线段的关系可得出关于a的一元二次方程,解方程即可得出结论.本题考查了反比例函数与一次函数的交点问题、两点间的距离公式以及解一元二次方程,解题的关键是找出线段OA、OC的长.
10.【答案】﹣20
【解析】【解答】解:∵正比例函数的图象与反比例函数y=﹣ 的图象交于A(x1,y1)、B(x2,y2)两点,关于原点对称,依此可得x1=﹣x2,y1=﹣y2,
∴(x2﹣x1)(y2﹣y1)
=x2y2﹣x2y1﹣x1y2+x1y1
=x2y2+x2y2+x1y1+x1y1
=﹣5×4
=﹣20.
故答案为:﹣20.
【分析】正比例函数的图象与反比例函数y=﹣ 的两交点坐标关于原点对称,依此可得x1=﹣x2,y1=﹣y2,将(x2﹣x1)(y2﹣y1)展开,依此关系即可求解.
11.【答案】32
【解析】【解答】过A作AM⊥x轴于M,过B作BN⊥x轴于N,
则∠AMO=∠BNC=90°,
∵四边形AOCB是菱形,
∴OA=BC=AB=OC,AB∥OC,OA∥BC,
∴∠AOM=∠BCN,
∵A(3,4),
∴OM=3,AM=4,由勾股定理得:OA=5,
即OC=OA=AB=BC=5,
在△AOM和△BCN中 ,
∴△AOM≌△BCN(AAS),
∴BN=AM=4,CN=OM=3,
∴ON=5+3=8,
即B点的坐标是(8,4),
把B的坐标代入y= ,
得:k=32,
故答案为:32.
【分析】过A作AM⊥x轴于M,过B作BN⊥x轴于N,根据菱形的性质及点A的坐标,可求出OA的长,再证明△AOM≌△BCN,得出BN、ON的长,就可求得点B的坐标,利用待定系数法,可求出反比例函数的解析式。
12.【答案】s=.
【解析】【解答】解:由题意得:底面积S关于高h的函数关系式是s=.
故本题答案为:s=.
【分析】根据等量关系“圆柱底面积=圆柱体积÷圆柱高”即可列出关系式.
13.【答案】解:把点 代入
当 时,
把 , 代入y1=kx+b
,
①-②得,
把 代入①得,
即
.
【解析】【分析】先把A点坐标代入 y2= ,求出反比例函数解析式,接着把 代入反比例函数求出B点坐标,最后把A、B两点坐标代入一次函数 y1=kx+b ,解出k、b即可得到一次函数解析式.
14.【答案】解: 点 在一次函数 的图象上,
点A的坐标为 .
又 点A在反比例函数 为常数, )的图象上,
反比例函数的表达式为 .
【解析】【分析】先将x=2代入一次函数 中可得,点A的坐标为 ,再将点A的坐标代入 可得反比例函数的解析式.
15.【答案】解:设A(m, )(m<0),
直线AB的解析式为y=ax(k≠0),
∵A(m, ),
∴ma= ,解得a= ,
∴直线AB的解析式为y= x.
∵AO的延长线交函数y= 的图象于点B,
∴B(﹣ mk,﹣ ),
∵△ABC的面积等于 ,CB⊥x轴,
∴ ×(﹣ )×(﹣ mk+|m|)= ,解得k1=﹣5(舍去),k2=3,
∴y2=
【解析】【分析】设A(m, )(m<0),则可得到直线AB的解析式为y= x.再利用反比例函数与一次函数的交点问题可表示出B(﹣ mk,﹣ ),则利用三角形面积公式得到 ×(﹣ )×(﹣ mk+|m|)= ,解得k1=﹣5(舍去),k2=3,于是得到y2= .
16.【答案】解:由题意得ut=2000,
整理得t=.
【解析】【分析】根据注水速度×注水时间=游泳池的容积可得ut=2000,变形即可求出t与u的函数解析式.
17.【答案】解:∵在矩形OABC中,OA=3,OC=2,∴B(3,2).∵F为AB的中点,∴F(3,1).∵点F在反比例函数 (k>0)的图象上,∴k=3,∴该函数的解析式为 (x>0)
【解析】【分析】根据矩形的性质由矩形的边长OA=3,OC=2得出B点的坐标,又F为AB的中点,故能得出F点的坐标,然后将F点的坐标代入反比例函数的解析式,即可求出比例系数K的值,从而得出反比例函数的解析式。
18.【答案】解:(1)∵E是矩形OABC对角线的交点,
∴OE=EB,
∵点B的坐标为(6,4),
∴E点的坐标是(3,2),
把x=3,y=2代入y=得k=6;
(2)设点D的坐标为(x,y),则S△OCD=OC×OD,
即S△OCD=xy=k,
由(1)知k=6,
∴S△OCD=k=3.
【解析】【分析】(1)由E是矩形OABC对角线的交点,得到OE=EB,由于点B的坐标为(6,4),于是得到E点的坐标是(3,2),即可得到结论;
(2)设点D的坐标为(x,y),即S△OCD=xy=k=3.
【能力提升答案】
1.【答案】C
【解析】【解答】解:∵点(3,﹣1)在反比例函数 的图象上,
∴k=3×(﹣1)=﹣3,
而1×3=﹣3×(﹣1)=3×1=3,﹣1×3=﹣3,
∴点(﹣1,3)在该反比例函数图象上.
故答案为:C.
【分析】先求出k=3×(﹣1)=﹣3,再求解即可。
2.【答案】A
【解析】【解答】解:如图:
由图象可知,函数图象经过点(6,1.5),
设反比例函数为 ,
则1.5= ,
解得k=9,
故答案为:A.
【分析】由题意可知图像过点(6,1.5),把这个点代入计算即可求解。
3.【答案】A
【解析】【分析】根据图象可以知道一次函数y1=k1x+b和反比例函数y2=(k1 k2≠0)的图象的交点的横坐标,若y1>y2,则根据图象可以确定x的取值范围.
【解答】如图,依题意得一次函数y1=k1x+b和反比例函数y2=(k1 k2≠0)的图象的交点的横坐标分别为x=-2或x=1,
若y1>y2,则y1的图象在y2的上面,
x的取值范围是-2<x<0或x>1.
故选A.
【点评】此题主要考查了反比例函数与一次函数的图象的交点问题,解题的关键是利用数形结合的方法解决问题.
4.【答案】A
【解析】【解答】解:∵反比例函数 的图象经过点 ,
∴ ,
即 ,
∴反比例函数的图象经过第一、三象限.
故答案为:A.
【分析】利用待定系数法求出k的值,可得到函数解析式,再利用反比例函数的图象与系数的关系可得答案.
5.【答案】C
【解析】【分析】设出反比例函数解析式,将P(-1,5)代入解析式求出k的值即可.
【解答】将P(-1,5)代入解析式y=得,
k=(-1)×5=-5,
解析式为:y=-.
故选C.
【点评】解答此题要明确待定系数法:现设某些未知的系数,然后根据已知条件求出未知系数的方法叫待定系数法.
6.【答案】B
【解析】【解答】由题意可得:﹣x+2= ,
所以x2﹣2x+1﹣6t=0,
∵两函数图象有两个交点,且两交点横坐标的积为负数,
∴
解不等式组,得t> .
故答案为:B.
【分析】联立函数解析式整理得到关于x的一元二次方程,则方程有两个不相等的实数根,即△>0,又由于横坐标的积为负数,则两个解的积为负数,根据根与系数关系可得关于t的不等式,联立求解可得t的范围.
7.【答案】y=
【解析】【解答】解:设该反比例函数的解析式为
将x= ,y=400代入,得
解得:k=100
∴眼镜度数与镜片焦距之间的函数关系式为
故答案为: .
【分析】设该反比例函数的解析式为 ,然后将x= ,y=400代入即可求出函数关系式.
8.【答案】12
【解析】【解答】解:∵点A(a,﹣6)在正比例函数y=3x的图象上,
∴﹣6=3a,
解得a=﹣2,
∴A(﹣2,﹣6)
∵点A(﹣2,﹣6)在反比例函数y= 的图象上,
∴k=﹣2×(﹣6)=12,
故答案为:12.
【分析】先根据y=3x求得A的坐标,再把点A的坐标代入反比例函数的解析式即可求出k的值.
9.【答案】8
【解析】【解答】解:∵反比例函数经过点(2,3)
∴k-2=2×3=6
解之:k=8
故答案为:8
【分析】把点(2,3)代入已知函数解析式,列出关于k的方程,通过解方程即可求得k的值。
10.【答案】x<﹣2或0<x<1
【解析】【解答】解:∵A(﹣2,1),B(1,﹣2),
由图象可知:一次函数的值大于反比例函数的值时x的取值范围是x<﹣2或0<x<1.
故答案为:x<﹣2或0<x<1.
【分析】根据两函数的交点坐标可知要使一次函数的值大于反比例函数的值,就要观察直线x=-2,x=0,x=1将两函数的图象分成四部分,观察函数图象可得出x的取值范围。
11.【答案】v=
【解析】【解答】解:∵一司机驾驶汽车从甲地去乙地,他以80千米/时的平均速度用了4小时到达乙地,那么路程为80×4=320千米,
∴汽车的速度v(千米/小时)与时间t(小时)的函数关系为v= .
故答案为v= .
【分析】先求得路程,再由等量关系“速度=路程÷时间”列出关系式即可.
12.【答案】
【解析】【解答】解:由题意得:人数x与完成任务所需的时间y之间的函数关系式为y=300÷15x=.
故本题答案为:y=.
【分析】根据等量关系“x个工人所需时间=工作总量÷x个工人工效”即可列出关系式.
13.【答案】解:在 中,令y=0,得 .解得 .∴直线 与x轴的交点A的坐标为:(-1,0)∴AO=1.∵OC=2AO,∴OC=2.∵BC⊥x轴于点C,∴点B的横坐标为2.∵点B在直线 上,∴ .∴点B的坐标为 .∵双曲线 过点B ,∴ .解得 .∴双曲线的解析式为
【解析】【分析】利用一次函数的值为0求出对应的x的值,就可得出点A的坐标,再根据OC=2OA,可得出OC的长,从而可得出点B的横坐标,将点B的横坐标代入一次函数解析式求出点B的纵坐标,即可得出点B的坐标,然后利用待定系数法,由点B的坐标就可求出双曲线的解析式。
14.【答案】解:(1)∵A(﹣2,﹣2)在y=上,∴m=4.∴反比例函数的解析式为y=.∵点B(n,4)在y=上,∴n=1.∴B(1,4).∵y=kx+b经过A(﹣2,﹣2),B(1,4),∴.解之得.∴一次函数的解析式为y=2x+2.(2)设C是直线AB与y轴的交点,∴当x=0时,y=2.∴点C(0,2).∴OC=2.∴S△AOB=S△ACO+S△BCO=×2×2+×2×1=3.
【解析】【分析】(1)把A(﹣2,﹣2)代入反比例函数y=,得出m的值,再把B(n,4)代入一次函数的解析式y=kx+b,运用待定系数法分别求其解析式;
(2)设直线AB与y轴交于点C,把三角形AOB的面积看成是三角形AOC和三角形OCB的面积之和进行计算.
15.【答案】解:(1)∵反比例函数y=(m≠0)过点B(1,﹣4),∴m=1×(﹣4)=﹣4,∴y=﹣,将x=﹣4,y=n代入反比例解析式得:n=1,∴A(﹣4,1),∴将A与B坐标代入一次函数解析式得:,解得:,∴y=﹣x﹣3;(2)在直线y=﹣x﹣3中,当y=0时,x=﹣3,∴C(﹣3,0),即OC=3,∴S△AOB=S△AOC+S△COB=(3×1+3×4)=;(3)不等式kx+b﹣<0的解集是﹣4<x<0或x>1.
【解析】【分析】(1)将B坐标代入反比例解析式中求出m的值,即可确定出反比例解析式;将A坐标代入反比例解析式求出n的值,确定出A的坐标,将A与B坐标代入一次函数解析式中求出k与b的值,即可确定出一次函数解析式;
(2)对于直线AB,令y=0求出x的值,即可确定出C坐标,三角形AOB面积=三角形AOC面积+三角形BOC面积,求出即可;
(3)由两函数交点A与B的横坐标,利用图象即可求出所求不等式的解集.
16.【答案】解:∵,当h为10cm时,底面积为30,
∴V=×10×30=100(cm3),
∴100=sh,
∴h关于s的函数解析式为:.
【解析】【分析】首先根据已知求出V的值,进而代入,即可得出h与s的函数关系式.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
