6.2 反比例函数的图像性质(基础复习 能力提升)同步复习小测 2022-2023学年北师大版数学九年级上册(Word版含答案)
文档属性
| 名称 | 6.2 反比例函数的图像性质(基础复习 能力提升)同步复习小测 2022-2023学年北师大版数学九年级上册(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 168.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-11 17:05:46 | ||
图片预览



文档简介
6.2反比例函数的图像性质---九年级同步复习小测(基础复习+能力提升)
【北师大版】
【基础复习】
一、单选题
1.下列图象中是反比例函数y=﹣ 图象的是( )
A. B.
C. D.
2.如果两点和在反比例函数的图象上,那么与间的关系是( )
A. B. C. D.
3.如图,在函数y1=(x<0)和y2=(x>0)的图象上,分别有A、B两点,若AB∥x轴,交y轴于点C,且OA⊥OB,S△AOC=,S△BOC=,则线段AB的长度是( )
A.8 B.9 C.10 D.11
4.若(x1,y1),(x2,y2),(x3,y3)都是y=的图象上的点,且x1<0<x2<x3.则下列各式正确的是( )
A.y1>y2>y3 B.y1<y2<y3 C.y2>y1>y3 D.y2<y3<y1
5.已知点P(1,m),Q(2,n)是反比例函数y= 图象上的两点,则( )
A.m<n<0 B.n<m<0 C.0<m<n D.0<n<m
6.若反比例函数 ,当 时,y随x的增大而增大,则k的取值范围是( )
A. B. C. D.
二、填空题
7.已知点 , 在反比例函数 的图象上,则 , 的大小关系是 .
8.如图,点在反比例函数的图象上,点在反比例函数的图象上,若轴,则的面积为 .
9.已知y是x的反比例函数,且当x=4,y=﹣1.
(1)函数y与x之间的函数表达式为 ;
(2)当一3≤x≤﹣时,y的取值范围是 ;
(3)若x>1时,y的取值范围是 ;
(4)若y<2时,x的取值范围是 .
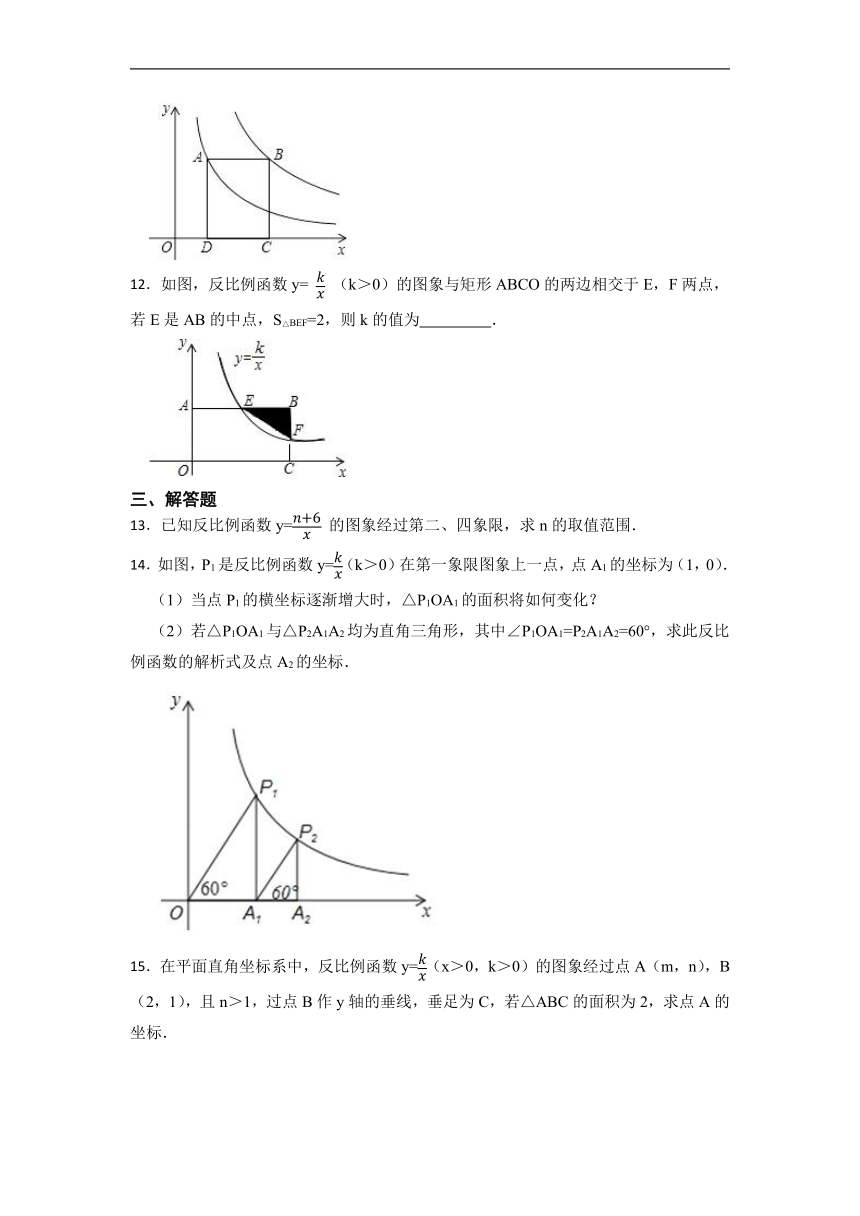
10.如图,P是反比例函数 图象上的一点, 轴于A,点B,C在y轴上,四边形PABC是平行四边形,则 PABC的面积是 .
11.如图,点A在双曲线 上,点B在双曲线 (k≠0)上,AB∥x轴,分别过点A,B向x轴作垂线,垂足分别为D、C,若矩形ABCD的面积是8,则k的值为 .
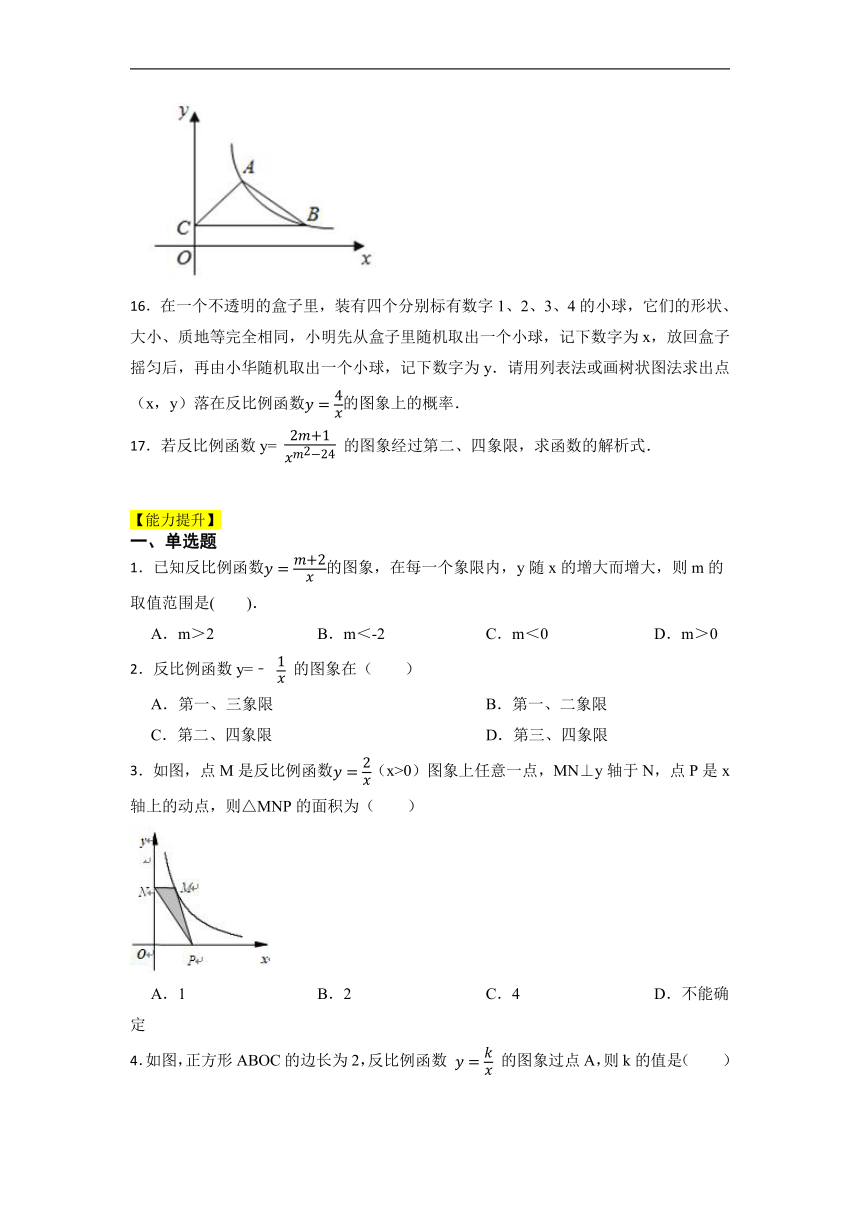
12.如图,反比例函数y= (k>0)的图象与矩形ABCO的两边相交于E,F两点,若E是AB的中点,S△BEF=2,则k的值为 .
三、解答题
13.已知反比例函数y= 的图象经过第二、四象限,求n的取值范围.
14.如图,P1是反比例函数y=(k>0)在第一象限图象上一点,点A1的坐标为(1,0).
(1)当点P1的横坐标逐渐增大时,△P1OA1的面积将如何变化?
(2)若△P1OA1与△P2A1A2均为直角三角形,其中∠P1OA1=P2A1A2=60°,求此反比例函数的解析式及点A2的坐标.
15.在平面直角坐标系中,反比例函数y=(x>0,k>0)的图象经过点A(m,n),B(2,1),且n>1,过点B作y轴的垂线,垂足为C,若△ABC的面积为2,求点A的坐标.
16.在一个不透明的盒子里,装有四个分别标有数字1、2、3、4的小球,它们的形状、大小、质地等完全相同,小明先从盒子里随机取出一个小球,记下数字为x,放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.请用列表法或画树状图法求出点(x,y)落在反比例函数的图象上的概率.
17.若反比例函数y= 的图象经过第二、四象限,求函数的解析式.
【能力提升】
一、单选题
1.已知反比例函数的图象,在每一个象限内,y随x的增大而增大,则m的取值范围是( ).
A.m>2 B.m<-2 C.m<0 D.m>0
2.反比例函数y=﹣ 的图象在( )
A.第一、三象限 B.第一、二象限
C.第二、四象限 D.第三、四象限
3.如图,点M是反比例函数(x>0)图象上任意一点,MN⊥y轴于N,点P是x轴上的动点,则△MNP的面积为( )
A.1 B.2 C.4 D.不能确定
4.如图,正方形ABOC的边长为2,反比例函数 的图象过点A,则k的值是( )
A.2 B.﹣2 C.4 D.﹣4
5.如图,平行于x轴的直线与函数 , 的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点,若 的面积为4,则 的值为
A.8 B. C.4 D.
6.已知反比例函数y=,若x≥5,则函数y有( )
A.最大值1 B.最小值1 C.最大值0 D.最小值0
二、填空题
7.若点A1(2,y1),A2(﹣2,y2)都在反比例函数 的图象上,则y1 y2(填>、<或=)
8.请写出一个位于第一、三象限的反比例函数表达式,y = .
9.点P,Q,R在反比例函数y=(常数k>0,x>0)图象上的位置如图所示,分别过这三个点作x轴,y轴的平行线.图中所构成的阴影部分面积从左到右依次为S1,S2,S3.若OF=FG= GA,S1+S3=10,则S2的值为 .
10.如图,过反比例函数 的图象上一点A作 轴于点B,连接 ,若 ,则 .
11.反比例函数y=,在每个象限内,y随x的增大而增大,则m的取值范围是 .
12.如图,在平面直角坐标系xOy中,函数y= (x>0)的图象经过点A,B,AC⊥x轴于点C,BD⊥y轴于点D,连接OA,OB,则△OAC与△OBD的面积之和为 .
三、解答题
13.在双曲线y= 的任一支上,y都随x的增大而增大,则k的取值范围.
14.已知x1,x2,x3是y= 图像上三个点的横坐标,且满足x3>x2>x1>0。请比较 与 的大小,并说明理由。
15.证明:任意一个反比例函数图象y=关于y=±x轴对称.
16.已知函数y=(k-2)为反比例函数.
(1)求k的值;
(2)它的图象在第几象限内,在各象限内,y随x增大而怎么 ;
(3)求出﹣2≤x≤﹣时,y的取值范围.
【基础复习答案】
1.【答案】C
【解析】【解答】反比例函数y=- 图象是双曲线,且位于第二、四象限.
故答案为:C.
【分析】根据反比例函数的性质:当k>0时,图像分支在第一、三象限,当k<0时,图像分支在第二、四象限,利用函数解析式可得结果。
2.【答案】D
【解析】【解答】解:把点代入反比例函数得,;
点代入反比例函数得,;
,
.
故答案为:D.
【分析】将点和代入求出和,再比较大小即可。
3.【答案】C
【解析】【解答】解:∵AB∥x轴,交y轴于点C,
∴S△AOC=|k1|=,S△BOC=|k2|=,
∴k1=﹣3,k2=27,
设C点坐标为(0,t),则A点坐标为(﹣,t),B点坐标为(,t),
∵OA⊥OB,
∴∠AOC+∠BOC=90°,
而∠AOC+∠OAC=90°,
∴∠OAC=∠BOC,
∴Rt△AOC∽Rt△OBC,
∴OC:BC=AC:OC,即t:=:t,解得t=3,
∴AB=+===10.
故选C.
【分析】根据反比例函数k的几何意义得到|k1|=,|k2|=,解得k1=﹣3,k2=27,设C点坐标为(0,t),则A点坐标为(﹣,t),B点坐标为(,t),
再证明Rt△AOC∽Rt△OBC,利用相似比得到t:=:t,解得t=3,然后计算AB=+即可.
4.【答案】D
【解析】【分析】根据反比例函数图象上点的特征,xy=3,所以得到x1 y1=-5,x2 y2=-5,x3 y3=-5,再根据x1<0<x2<x3,即可判断y1、y2、y3的大小关系.
【解答】∵A(x1,y1),B(x2,y2),C(x3,y3)是反比例函数y=
图象上的点,
∴x1 y1=-5,x2 y2=-5,x3 y3=-5,
∵0<x2<x3,
∴y2∵x1<0,
∴y1>0,
∴y1>y3>y2.
故选D.
【点评】此题主要考查了反比例函数图象上点的特征,凡是在反比例函数图象上的点,横纵坐标的乘积是一个定值k.
5.【答案】D
【解析】【解答】解:∵y= 中k=6>0,
∴此函数图象的两个分支分别位于第一、三象限,且在每一象限内y随x的增大而减小,
∵1<2,
∴0<n<m,
故答案为:D.
【分析】根据反比例函数的k的符号得出函数的增减性,由题可知点P和点Q在第一象限,即可得出结果.
6.【答案】D
【解析】【解答】解:根据题意,当 时,y随x的增大而增大,
图象在第二象限,
,
故答案为:D.
【分析】当 时,y随x的增大而增大,即可得出图象在第二象限,可得出k的取值范围。
7.【答案】
【解析】【解答】∵反比例函数中y=- 中 ,
∴此函数的图象在二、四象限内,在每个象限内,y随x的增大而增大,
∵0<1<2,
∴A、B两点均在第四象限,
∴a<b.
故答案为:a<b.
【分析】由反比例函数y=- 可知函数的图象在第二、第四象限内,可以知道在每个象限内,y随x的增大而增大,根据这个判定则可.
8.【答案】3
【解析】【解答】解:如图,设PQ与y轴相交于点M,
∵PQ∥x轴,
∴
故答案为:3.
【分析】利用反比例函数k的几何意义和割补法可得。
9.【答案】y=﹣ ;≤x≤8 ;﹣4<y<0;x>0或x<﹣2
【解析】【解答】解:(1)设反比例函数的解析式为y=,
∵当x=4,y=﹣1,
∴k=﹣1×4=﹣4,
∴反比例函数的解析式为y=﹣;
(2)当一3≤x≤﹣时,y=﹣连续递增
又当x=﹣3时,y=,当x=﹣时,y=8,
∴当一3≤x≤﹣时,y的取值范围是≤x≤8;
(3)当x=1时,y=﹣4,
∵k=﹣4,在每一象限内y随着x的增大而增大,
∴当x>1时,y的取值范围是﹣4<y<0;
(4)当y=2时,x=﹣2,
∵k=﹣4,在每一象限内y随着x的增大而增大,
∴当y<2时,y的取值范围是x>0或x<﹣2;
故答案为:y=﹣;≤x≤8;﹣4<y<0;x>0或x<﹣2.
【分析】(1)利用待定系数法确定反比例函数的解析式即可;
(2)根据自变量的取值范围确定函数值的取值范围即可;
(3)根据自变量的取值范围确定函数值的取值范围即可;
(4)根据函数值的取值范围确定自变量的取值范围即可.
10.【答案】6
【解析】【解答】作PD⊥BC,
所以,设P(x,y).
由 ,
得平行四边形面积=BC PD=xy=6.
故答案为:6
【分析】作PD⊥BC,根据三个角为直角的四边形是矩形可得四边形OAPD是矩形,根据反比例函数k的几何意义可得S矩形OAPD=6,由平行四边形的面积公式可得平行四边形面积=BC PD=S矩形OAPD=6.
11.【答案】12
【解析】【解答】解:过点A作AE⊥y轴于点E,
∵点A在双曲线 上,
∴矩形EODA的面积为:4,
∵矩形ABCD的面积是8,
∴矩形EOCB的面积为:4+8=12,
则k的值为:xy=k=12.
故答案为:12.
【分析】首先求出矩形EODA的面积,利用矩形ABCD的面积是8,可得矩形EOCB的面积为4+8=12,再利用xy=k求出k的值即可.
12.【答案】8
【解析】【解答】解:设E(a, ),则B纵坐标也为 ,
E是AB中点,所以F点横坐标为2a,代入解析式得到纵坐标: ,
因为BF=BC﹣FC= ﹣ = ,所以F也为中点,
S△BEF=2= ,k=8.
故答案是:8.
【分析】设E(a, ),则B纵坐标也为 ,代入反比例函数的y= ,即可求得F的横坐标,则根据三角形的面积公式即可求得k的值.
13.【答案】解:反比例函数y= 的图象经过第二、四象限,
∴n+6<0,
∴n<-6
【解析】【分析】反比例函数中,当k<0时,反比例函数图象位于第二、四象限,据此可得n+6<0 即可得出答案.
14.【答案】解:(1)过P1作P1C⊥OA1,垂足为C,设P1(a,b),∵P1在第一象限,∴△P1OA1的面积=×0A1×b=b.又∵当k>0时,在每一个象限内,y随x的增大而减小.故当点P1的横坐标逐渐增大时,其纵坐标逐渐减小,则△P1OA1的面积将逐渐减小.(2)因为△P1OA1是直角三角形,所以OA1=1,P1A1=,所以P1(1,).代入y=,得k=,所以反比例函数的解析式为y=.∵△P2A1A2为直角三角形,∠P2A1A2=60°,∴P2A2⊥x轴,设A1A2=a,则OA2=1+a,P2A2=a,所以P2(1+a,a).∵P2(1+a,a)在反比例函数的图象上,∴代入y=,得(1+a) a=,化简得a2+2a﹣1=0解得:a=∵a>0,∴a=∴A1A2=∴OA2=OA1+A1A2=所以点A2的坐标为(,0).
【解析】【分析】(1)设P1(a,b),根据反比例函数的图象性质,可知y随x的增大而减小.又△P1OA1的面积=×0A1×b=b.故当点P1的横坐标逐渐增大时,△P1OA1的面积将逐渐减小;
(2)因为△P1OA1是直角三角形,所以OA1=1,P1A1=,所以P1(1,).代入y=,得k=,所以反比例函数的解析式为y=,由于△P2A1A2为直角三角形,∠2A1A2=60°,设A1A2=a,则OA2=1+a,P2A2=a,可用含a的代数式分别表示点P2的横、纵坐标,再代入反比例函数的解析式中,求出a的值,进而得出A2点的坐标.
15.【答案】解:∵B(2,1),
∴BC=2,
∵△ABC的面积为2,
∴×2×(n﹣1)=2,
解得:n=3,
∵B(2,1),∴k=2,
反比例函数解析式为:y=,
∴n=3时,m=,
∴点A的坐标为(,3).
【解析】【分析】根据图象和△ABC的面积求出n的值,根据B(2,1),求出反比例函数的解析式,把n代入解析式求出m即可.
16.【答案】解:由题意,可列表:
第一次\第二次 1 2 3 4
1 (1,1) (1,2) (1,3) (1,4)
2 (2,1) (2,2) (2,3) (2,4)
3 (3,1) (3,2) (3,3) (3,4)
4 (4,1) (4,2) (4,3) (4,4)
由已知,共有16种结果,且每种结果出现的可能性相同,其中满足要求的有3种,
∴P(点落在双曲线的图象上)=.
【解析】【分析】利用列表法求出所有点,找出满足要求的点,即可求出。
17.【答案】解:根据题意得: ,
解得:m=﹣5
则函数的解析式是:y=﹣
【解析】【分析】根据反比例函数的定义,可以得到m2﹣24=1,而图象经过第二、四象限,则比例系数是负数,据此即可求解.
【能力提升答案】
1.【答案】B
【解析】【分析】先根据反比例函数的图象在每一个象限内,y随x的增大而增大得出关于k的不等式,求出k的取值范围即可.
【解答】∵反比例函数y=的图象在每一个象限内,y随x的增大而增大,
∴m+2<0,
∴m<-2.
故答案为:B
2.【答案】C
【解析】【解答】解:∵k=﹣1,
∴图象在第二、四象限,
故选:C.
【分析】根据反比例函数y= (k≠0)的图象是双曲线;当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大进行解答.
3.【答案】A
【解析】【分析】延长NM,作PA⊥MN,设M的坐标为(x,y),由题意可知,S△MNP=MN×PA=xy,因为点M在反比例函数,xy=2,所以xy=1,故选A.
【点评】该题考的是常考的知识点,考查学生对反比例函数k的几何意义的掌握,要求学生必须熟练。
4.【答案】D
【解析】【解答】解:因为图象在第二象限,
所以k<0,
根据反比例函数系数k的几何意义可知|k|=2×2=4,
所以k=﹣4.
故答案为:D.
【分析】观察图像,可知双曲线分布在第二、四象限,根据正方形ABOC的边长为2,得出其面积为4,即可得k的值。
5.【答案】A
【解析】【解答】 轴,
,B两点纵坐标相同,
设 , ,则 , ,
,
,
故答案为:A.
【分析】设 , ,根据反比例函数图象上点的坐标特征得出 , 根据三角形的面积公式得到 ,即可求出 .
6.【答案】A
【解析】【解答】解:∵y=,
∴反比例函数在第一象限内,y随x的增大而减小,
∴当x≥5时,y≤1,
∴y有最大值1.
故答案为:A.
【分析】根据反比例函数图象增减性与k符号关系,即k>0时,在第一、三象限内,y随x的增大而减小,∵k=5>0,所以当x≥5时,y≤1,即y有最大值1,即可得出正确答案.
7.【答案】>
【解析】【解答】解:因为点A1(2,y1),A2(﹣2,y2)都在反比例函数 的图象上,
由2>0,可知:反比例函数图象过一,三象限,
则y1>y2.
故答案为:>.
【分析】根据反比例函数的性质即可得结论.
8.【答案】 (答案不唯一)
【解析】【解答】解:设反比例函数解析式为 ,
∵图象位于第一、三象限,∴k>0,
∴可写解析式为 (答案不唯一).
故答案为: (答案不唯一).
【分析】利用反比例函数的性质,当k>0时,图象分支在第一、三象限,由此可得答案.
9.【答案】2
【解析】【解答】解:∵OF=FG=AG,
∴四边形AOER的面积=3S1,四边形DERH的面积=3S2,四边形CBHD的面积=3S3,
∴,,,
即,,.
∵,
∴,
解得.
∴.
故答案为:2.
【分析】由题意可得SAOER=3S1,SDERH=3S2,SCBHD=3S3,结合反比例函数k的几何意义可得3S1=k,2S1+2S2=k,S1+S2+S3=k,然后表示出S1、S2、S3,结合S1+S3=10可求出k的值,进而可得S2.
10.【答案】-6
【解析】【解答】解:∵ 轴, ,
∴ ,
∴ ,
∵ ,
∴ ;
故答案为-6.
【分析】直接根据反比例函数的几何意义即可解答.
11.【答案】m<1
【解析】【解答】解:由题意得 y=的图象在每个象限内y随x的增大而增大,
则m﹣1<0,
即m<1.
故答案为:m<1.
【分析】由于反比例函数y= 的图象在每个象限内y随x的增大而增大,则满足m﹣1<0即可.
12.【答案】2
【解析】【解答】解:在函数 中k=2,
∴S△OAC= S△OAD= =1,
∴S△OAC+ S△OBD=2
【分析】由反比例函数中k值的含义,可知△OAC与△OBD的面积为1,则可求出答案.
13.【答案】解:∵y都随x的增大而增大,
∴此函数的图象在二、四象限,
∴1﹣k<0,
∴k>1
【解析】【分析】先根据已知反比例函数的增减性判断出1﹣k的符号,再求出k的取值范围即可.
14.【答案】解:∵第一象限反比例函数值随自变量的增大而减小
x3>x2>x1>0
∴ ,
∴
【解析】【分析】利用反比例函数的性质,观察函数图象可知已知三个点在第一象限,由此可得反比例函数值随自变量的增大而减小,再根据x3>x2>x1>0,就看确定出 与 的大小关系。
15.【答案】证明:设P(a,b)为反比例函数图象y=上任意一点,则ab=k,
点P关于直线y=x的对称点为(b,a),由于b a=ab=k,所以点(b,a)在反比例函数y=的图象上,即反比例函数图象y=关于y=x轴对称;
点P关于直线y=﹣x的对称点为(﹣b,﹣a),由于﹣b (﹣a)=ab=k,所以点(﹣b,﹣a)在反比例函数y=的图象上,即反比例函数图象y=关于y=﹣x轴对称,
即任意一个反比例函数图象y=关于y=±x轴对称.
【解析】【分析】利用反比例函数图象上任意一点关于y=±x轴对称点还在反比例函数y=图象上进行证明.
16.【答案】解:(1)由题意得:k2﹣5=﹣1,
解得:k=±2,
∵k﹣2≠0,
∴k=﹣2;
(2)∵k=﹣2<0,
∴反比例函数的图象在二、四象限,在各象限内,y随着x增大而增大;
故答案为:二、四,增大;
(3)∵反比例函数表达式为y=-,
∴当x=﹣2时,y=2,当x=-时,y=8,
∴当﹣2≤x≤﹣时,2≤y≤8.
【解析】【分析】(1)根据反比例函数的定义确定k的值即可;
(2)根据反比例函数的性质结合求得的k的符号描述其图象的位置及增减性即可;
(3)分别代入自变量的值结合其增减性即可确定函数值的取值范围.
【北师大版】
【基础复习】
一、单选题
1.下列图象中是反比例函数y=﹣ 图象的是( )
A. B.
C. D.
2.如果两点和在反比例函数的图象上,那么与间的关系是( )
A. B. C. D.
3.如图,在函数y1=(x<0)和y2=(x>0)的图象上,分别有A、B两点,若AB∥x轴,交y轴于点C,且OA⊥OB,S△AOC=,S△BOC=,则线段AB的长度是( )
A.8 B.9 C.10 D.11
4.若(x1,y1),(x2,y2),(x3,y3)都是y=的图象上的点,且x1<0<x2<x3.则下列各式正确的是( )
A.y1>y2>y3 B.y1<y2<y3 C.y2>y1>y3 D.y2<y3<y1
5.已知点P(1,m),Q(2,n)是反比例函数y= 图象上的两点,则( )
A.m<n<0 B.n<m<0 C.0<m<n D.0<n<m
6.若反比例函数 ,当 时,y随x的增大而增大,则k的取值范围是( )
A. B. C. D.
二、填空题
7.已知点 , 在反比例函数 的图象上,则 , 的大小关系是 .
8.如图,点在反比例函数的图象上,点在反比例函数的图象上,若轴,则的面积为 .
9.已知y是x的反比例函数,且当x=4,y=﹣1.
(1)函数y与x之间的函数表达式为 ;
(2)当一3≤x≤﹣时,y的取值范围是 ;
(3)若x>1时,y的取值范围是 ;
(4)若y<2时,x的取值范围是 .
10.如图,P是反比例函数 图象上的一点, 轴于A,点B,C在y轴上,四边形PABC是平行四边形,则 PABC的面积是 .
11.如图,点A在双曲线 上,点B在双曲线 (k≠0)上,AB∥x轴,分别过点A,B向x轴作垂线,垂足分别为D、C,若矩形ABCD的面积是8,则k的值为 .
12.如图,反比例函数y= (k>0)的图象与矩形ABCO的两边相交于E,F两点,若E是AB的中点,S△BEF=2,则k的值为 .
三、解答题
13.已知反比例函数y= 的图象经过第二、四象限,求n的取值范围.
14.如图,P1是反比例函数y=(k>0)在第一象限图象上一点,点A1的坐标为(1,0).
(1)当点P1的横坐标逐渐增大时,△P1OA1的面积将如何变化?
(2)若△P1OA1与△P2A1A2均为直角三角形,其中∠P1OA1=P2A1A2=60°,求此反比例函数的解析式及点A2的坐标.
15.在平面直角坐标系中,反比例函数y=(x>0,k>0)的图象经过点A(m,n),B(2,1),且n>1,过点B作y轴的垂线,垂足为C,若△ABC的面积为2,求点A的坐标.
16.在一个不透明的盒子里,装有四个分别标有数字1、2、3、4的小球,它们的形状、大小、质地等完全相同,小明先从盒子里随机取出一个小球,记下数字为x,放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.请用列表法或画树状图法求出点(x,y)落在反比例函数的图象上的概率.
17.若反比例函数y= 的图象经过第二、四象限,求函数的解析式.
【能力提升】
一、单选题
1.已知反比例函数的图象,在每一个象限内,y随x的增大而增大,则m的取值范围是( ).
A.m>2 B.m<-2 C.m<0 D.m>0
2.反比例函数y=﹣ 的图象在( )
A.第一、三象限 B.第一、二象限
C.第二、四象限 D.第三、四象限
3.如图,点M是反比例函数(x>0)图象上任意一点,MN⊥y轴于N,点P是x轴上的动点,则△MNP的面积为( )
A.1 B.2 C.4 D.不能确定
4.如图,正方形ABOC的边长为2,反比例函数 的图象过点A,则k的值是( )
A.2 B.﹣2 C.4 D.﹣4
5.如图,平行于x轴的直线与函数 , 的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点,若 的面积为4,则 的值为
A.8 B. C.4 D.
6.已知反比例函数y=,若x≥5,则函数y有( )
A.最大值1 B.最小值1 C.最大值0 D.最小值0
二、填空题
7.若点A1(2,y1),A2(﹣2,y2)都在反比例函数 的图象上,则y1 y2(填>、<或=)
8.请写出一个位于第一、三象限的反比例函数表达式,y = .
9.点P,Q,R在反比例函数y=(常数k>0,x>0)图象上的位置如图所示,分别过这三个点作x轴,y轴的平行线.图中所构成的阴影部分面积从左到右依次为S1,S2,S3.若OF=FG= GA,S1+S3=10,则S2的值为 .
10.如图,过反比例函数 的图象上一点A作 轴于点B,连接 ,若 ,则 .
11.反比例函数y=,在每个象限内,y随x的增大而增大,则m的取值范围是 .
12.如图,在平面直角坐标系xOy中,函数y= (x>0)的图象经过点A,B,AC⊥x轴于点C,BD⊥y轴于点D,连接OA,OB,则△OAC与△OBD的面积之和为 .
三、解答题
13.在双曲线y= 的任一支上,y都随x的增大而增大,则k的取值范围.
14.已知x1,x2,x3是y= 图像上三个点的横坐标,且满足x3>x2>x1>0。请比较 与 的大小,并说明理由。
15.证明:任意一个反比例函数图象y=关于y=±x轴对称.
16.已知函数y=(k-2)为反比例函数.
(1)求k的值;
(2)它的图象在第几象限内,在各象限内,y随x增大而怎么 ;
(3)求出﹣2≤x≤﹣时,y的取值范围.
【基础复习答案】
1.【答案】C
【解析】【解答】反比例函数y=- 图象是双曲线,且位于第二、四象限.
故答案为:C.
【分析】根据反比例函数的性质:当k>0时,图像分支在第一、三象限,当k<0时,图像分支在第二、四象限,利用函数解析式可得结果。
2.【答案】D
【解析】【解答】解:把点代入反比例函数得,;
点代入反比例函数得,;
,
.
故答案为:D.
【分析】将点和代入求出和,再比较大小即可。
3.【答案】C
【解析】【解答】解:∵AB∥x轴,交y轴于点C,
∴S△AOC=|k1|=,S△BOC=|k2|=,
∴k1=﹣3,k2=27,
设C点坐标为(0,t),则A点坐标为(﹣,t),B点坐标为(,t),
∵OA⊥OB,
∴∠AOC+∠BOC=90°,
而∠AOC+∠OAC=90°,
∴∠OAC=∠BOC,
∴Rt△AOC∽Rt△OBC,
∴OC:BC=AC:OC,即t:=:t,解得t=3,
∴AB=+===10.
故选C.
【分析】根据反比例函数k的几何意义得到|k1|=,|k2|=,解得k1=﹣3,k2=27,设C点坐标为(0,t),则A点坐标为(﹣,t),B点坐标为(,t),
再证明Rt△AOC∽Rt△OBC,利用相似比得到t:=:t,解得t=3,然后计算AB=+即可.
4.【答案】D
【解析】【分析】根据反比例函数图象上点的特征,xy=3,所以得到x1 y1=-5,x2 y2=-5,x3 y3=-5,再根据x1<0<x2<x3,即可判断y1、y2、y3的大小关系.
【解答】∵A(x1,y1),B(x2,y2),C(x3,y3)是反比例函数y=
图象上的点,
∴x1 y1=-5,x2 y2=-5,x3 y3=-5,
∵0<x2<x3,
∴y2
∴y1>0,
∴y1>y3>y2.
故选D.
【点评】此题主要考查了反比例函数图象上点的特征,凡是在反比例函数图象上的点,横纵坐标的乘积是一个定值k.
5.【答案】D
【解析】【解答】解:∵y= 中k=6>0,
∴此函数图象的两个分支分别位于第一、三象限,且在每一象限内y随x的增大而减小,
∵1<2,
∴0<n<m,
故答案为:D.
【分析】根据反比例函数的k的符号得出函数的增减性,由题可知点P和点Q在第一象限,即可得出结果.
6.【答案】D
【解析】【解答】解:根据题意,当 时,y随x的增大而增大,
图象在第二象限,
,
故答案为:D.
【分析】当 时,y随x的增大而增大,即可得出图象在第二象限,可得出k的取值范围。
7.【答案】
【解析】【解答】∵反比例函数中y=- 中 ,
∴此函数的图象在二、四象限内,在每个象限内,y随x的增大而增大,
∵0<1<2,
∴A、B两点均在第四象限,
∴a<b.
故答案为:a<b.
【分析】由反比例函数y=- 可知函数的图象在第二、第四象限内,可以知道在每个象限内,y随x的增大而增大,根据这个判定则可.
8.【答案】3
【解析】【解答】解:如图,设PQ与y轴相交于点M,
∵PQ∥x轴,
∴
故答案为:3.
【分析】利用反比例函数k的几何意义和割补法可得。
9.【答案】y=﹣ ;≤x≤8 ;﹣4<y<0;x>0或x<﹣2
【解析】【解答】解:(1)设反比例函数的解析式为y=,
∵当x=4,y=﹣1,
∴k=﹣1×4=﹣4,
∴反比例函数的解析式为y=﹣;
(2)当一3≤x≤﹣时,y=﹣连续递增
又当x=﹣3时,y=,当x=﹣时,y=8,
∴当一3≤x≤﹣时,y的取值范围是≤x≤8;
(3)当x=1时,y=﹣4,
∵k=﹣4,在每一象限内y随着x的增大而增大,
∴当x>1时,y的取值范围是﹣4<y<0;
(4)当y=2时,x=﹣2,
∵k=﹣4,在每一象限内y随着x的增大而增大,
∴当y<2时,y的取值范围是x>0或x<﹣2;
故答案为:y=﹣;≤x≤8;﹣4<y<0;x>0或x<﹣2.
【分析】(1)利用待定系数法确定反比例函数的解析式即可;
(2)根据自变量的取值范围确定函数值的取值范围即可;
(3)根据自变量的取值范围确定函数值的取值范围即可;
(4)根据函数值的取值范围确定自变量的取值范围即可.
10.【答案】6
【解析】【解答】作PD⊥BC,
所以,设P(x,y).
由 ,
得平行四边形面积=BC PD=xy=6.
故答案为:6
【分析】作PD⊥BC,根据三个角为直角的四边形是矩形可得四边形OAPD是矩形,根据反比例函数k的几何意义可得S矩形OAPD=6,由平行四边形的面积公式可得平行四边形面积=BC PD=S矩形OAPD=6.
11.【答案】12
【解析】【解答】解:过点A作AE⊥y轴于点E,
∵点A在双曲线 上,
∴矩形EODA的面积为:4,
∵矩形ABCD的面积是8,
∴矩形EOCB的面积为:4+8=12,
则k的值为:xy=k=12.
故答案为:12.
【分析】首先求出矩形EODA的面积,利用矩形ABCD的面积是8,可得矩形EOCB的面积为4+8=12,再利用xy=k求出k的值即可.
12.【答案】8
【解析】【解答】解:设E(a, ),则B纵坐标也为 ,
E是AB中点,所以F点横坐标为2a,代入解析式得到纵坐标: ,
因为BF=BC﹣FC= ﹣ = ,所以F也为中点,
S△BEF=2= ,k=8.
故答案是:8.
【分析】设E(a, ),则B纵坐标也为 ,代入反比例函数的y= ,即可求得F的横坐标,则根据三角形的面积公式即可求得k的值.
13.【答案】解:反比例函数y= 的图象经过第二、四象限,
∴n+6<0,
∴n<-6
【解析】【分析】反比例函数中,当k<0时,反比例函数图象位于第二、四象限,据此可得n+6<0 即可得出答案.
14.【答案】解:(1)过P1作P1C⊥OA1,垂足为C,设P1(a,b),∵P1在第一象限,∴△P1OA1的面积=×0A1×b=b.又∵当k>0时,在每一个象限内,y随x的增大而减小.故当点P1的横坐标逐渐增大时,其纵坐标逐渐减小,则△P1OA1的面积将逐渐减小.(2)因为△P1OA1是直角三角形,所以OA1=1,P1A1=,所以P1(1,).代入y=,得k=,所以反比例函数的解析式为y=.∵△P2A1A2为直角三角形,∠P2A1A2=60°,∴P2A2⊥x轴,设A1A2=a,则OA2=1+a,P2A2=a,所以P2(1+a,a).∵P2(1+a,a)在反比例函数的图象上,∴代入y=,得(1+a) a=,化简得a2+2a﹣1=0解得:a=∵a>0,∴a=∴A1A2=∴OA2=OA1+A1A2=所以点A2的坐标为(,0).
【解析】【分析】(1)设P1(a,b),根据反比例函数的图象性质,可知y随x的增大而减小.又△P1OA1的面积=×0A1×b=b.故当点P1的横坐标逐渐增大时,△P1OA1的面积将逐渐减小;
(2)因为△P1OA1是直角三角形,所以OA1=1,P1A1=,所以P1(1,).代入y=,得k=,所以反比例函数的解析式为y=,由于△P2A1A2为直角三角形,∠2A1A2=60°,设A1A2=a,则OA2=1+a,P2A2=a,可用含a的代数式分别表示点P2的横、纵坐标,再代入反比例函数的解析式中,求出a的值,进而得出A2点的坐标.
15.【答案】解:∵B(2,1),
∴BC=2,
∵△ABC的面积为2,
∴×2×(n﹣1)=2,
解得:n=3,
∵B(2,1),∴k=2,
反比例函数解析式为:y=,
∴n=3时,m=,
∴点A的坐标为(,3).
【解析】【分析】根据图象和△ABC的面积求出n的值,根据B(2,1),求出反比例函数的解析式,把n代入解析式求出m即可.
16.【答案】解:由题意,可列表:
第一次\第二次 1 2 3 4
1 (1,1) (1,2) (1,3) (1,4)
2 (2,1) (2,2) (2,3) (2,4)
3 (3,1) (3,2) (3,3) (3,4)
4 (4,1) (4,2) (4,3) (4,4)
由已知,共有16种结果,且每种结果出现的可能性相同,其中满足要求的有3种,
∴P(点落在双曲线的图象上)=.
【解析】【分析】利用列表法求出所有点,找出满足要求的点,即可求出。
17.【答案】解:根据题意得: ,
解得:m=﹣5
则函数的解析式是:y=﹣
【解析】【分析】根据反比例函数的定义,可以得到m2﹣24=1,而图象经过第二、四象限,则比例系数是负数,据此即可求解.
【能力提升答案】
1.【答案】B
【解析】【分析】先根据反比例函数的图象在每一个象限内,y随x的增大而增大得出关于k的不等式,求出k的取值范围即可.
【解答】∵反比例函数y=的图象在每一个象限内,y随x的增大而增大,
∴m+2<0,
∴m<-2.
故答案为:B
2.【答案】C
【解析】【解答】解:∵k=﹣1,
∴图象在第二、四象限,
故选:C.
【分析】根据反比例函数y= (k≠0)的图象是双曲线;当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大进行解答.
3.【答案】A
【解析】【分析】延长NM,作PA⊥MN,设M的坐标为(x,y),由题意可知,S△MNP=MN×PA=xy,因为点M在反比例函数,xy=2,所以xy=1,故选A.
【点评】该题考的是常考的知识点,考查学生对反比例函数k的几何意义的掌握,要求学生必须熟练。
4.【答案】D
【解析】【解答】解:因为图象在第二象限,
所以k<0,
根据反比例函数系数k的几何意义可知|k|=2×2=4,
所以k=﹣4.
故答案为:D.
【分析】观察图像,可知双曲线分布在第二、四象限,根据正方形ABOC的边长为2,得出其面积为4,即可得k的值。
5.【答案】A
【解析】【解答】 轴,
,B两点纵坐标相同,
设 , ,则 , ,
,
,
故答案为:A.
【分析】设 , ,根据反比例函数图象上点的坐标特征得出 , 根据三角形的面积公式得到 ,即可求出 .
6.【答案】A
【解析】【解答】解:∵y=,
∴反比例函数在第一象限内,y随x的增大而减小,
∴当x≥5时,y≤1,
∴y有最大值1.
故答案为:A.
【分析】根据反比例函数图象增减性与k符号关系,即k>0时,在第一、三象限内,y随x的增大而减小,∵k=5>0,所以当x≥5时,y≤1,即y有最大值1,即可得出正确答案.
7.【答案】>
【解析】【解答】解:因为点A1(2,y1),A2(﹣2,y2)都在反比例函数 的图象上,
由2>0,可知:反比例函数图象过一,三象限,
则y1>y2.
故答案为:>.
【分析】根据反比例函数的性质即可得结论.
8.【答案】 (答案不唯一)
【解析】【解答】解:设反比例函数解析式为 ,
∵图象位于第一、三象限,∴k>0,
∴可写解析式为 (答案不唯一).
故答案为: (答案不唯一).
【分析】利用反比例函数的性质,当k>0时,图象分支在第一、三象限,由此可得答案.
9.【答案】2
【解析】【解答】解:∵OF=FG=AG,
∴四边形AOER的面积=3S1,四边形DERH的面积=3S2,四边形CBHD的面积=3S3,
∴,,,
即,,.
∵,
∴,
解得.
∴.
故答案为:2.
【分析】由题意可得SAOER=3S1,SDERH=3S2,SCBHD=3S3,结合反比例函数k的几何意义可得3S1=k,2S1+2S2=k,S1+S2+S3=k,然后表示出S1、S2、S3,结合S1+S3=10可求出k的值,进而可得S2.
10.【答案】-6
【解析】【解答】解:∵ 轴, ,
∴ ,
∴ ,
∵ ,
∴ ;
故答案为-6.
【分析】直接根据反比例函数的几何意义即可解答.
11.【答案】m<1
【解析】【解答】解:由题意得 y=的图象在每个象限内y随x的增大而增大,
则m﹣1<0,
即m<1.
故答案为:m<1.
【分析】由于反比例函数y= 的图象在每个象限内y随x的增大而增大,则满足m﹣1<0即可.
12.【答案】2
【解析】【解答】解:在函数 中k=2,
∴S△OAC= S△OAD= =1,
∴S△OAC+ S△OBD=2
【分析】由反比例函数中k值的含义,可知△OAC与△OBD的面积为1,则可求出答案.
13.【答案】解:∵y都随x的增大而增大,
∴此函数的图象在二、四象限,
∴1﹣k<0,
∴k>1
【解析】【分析】先根据已知反比例函数的增减性判断出1﹣k的符号,再求出k的取值范围即可.
14.【答案】解:∵第一象限反比例函数值随自变量的增大而减小
x3>x2>x1>0
∴ ,
∴
【解析】【分析】利用反比例函数的性质,观察函数图象可知已知三个点在第一象限,由此可得反比例函数值随自变量的增大而减小,再根据x3>x2>x1>0,就看确定出 与 的大小关系。
15.【答案】证明:设P(a,b)为反比例函数图象y=上任意一点,则ab=k,
点P关于直线y=x的对称点为(b,a),由于b a=ab=k,所以点(b,a)在反比例函数y=的图象上,即反比例函数图象y=关于y=x轴对称;
点P关于直线y=﹣x的对称点为(﹣b,﹣a),由于﹣b (﹣a)=ab=k,所以点(﹣b,﹣a)在反比例函数y=的图象上,即反比例函数图象y=关于y=﹣x轴对称,
即任意一个反比例函数图象y=关于y=±x轴对称.
【解析】【分析】利用反比例函数图象上任意一点关于y=±x轴对称点还在反比例函数y=图象上进行证明.
16.【答案】解:(1)由题意得:k2﹣5=﹣1,
解得:k=±2,
∵k﹣2≠0,
∴k=﹣2;
(2)∵k=﹣2<0,
∴反比例函数的图象在二、四象限,在各象限内,y随着x增大而增大;
故答案为:二、四,增大;
(3)∵反比例函数表达式为y=-,
∴当x=﹣2时,y=2,当x=-时,y=8,
∴当﹣2≤x≤﹣时,2≤y≤8.
【解析】【分析】(1)根据反比例函数的定义确定k的值即可;
(2)根据反比例函数的性质结合求得的k的符号描述其图象的位置及增减性即可;
(3)分别代入自变量的值结合其增减性即可确定函数值的取值范围.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
