北师大版数学五年级下册单元测试卷 第七单元 用方程解问题(含答案)
文档属性
| 名称 | 北师大版数学五年级下册单元测试卷 第七单元 用方程解问题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 121.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 10:11:17 | ||
图片预览




文档简介
北师大版数学五年级下册单元测试卷
第七单元 用方程解问题
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 五 总分
得分
一、选择题
1.一条裙子和一条裤子共92元,一条裙子的价格是一条裤子的3倍,设一条裤子的售价是元,根据这些条件,列出的方程正确的是( )。
A. B. C.
2.小敏和小华买同样的冬奥会明信片,小敏买了15套,小华买了8套,小敏和小华一共花了368元,求每套明信片多少元。解:设每套明信片x元,下列方程正确的是( )。
A. B. C.
3.王顺和李小军同时从两地沿一条公路面对面走来。王顺的速度是73米分,李小军的速度是88米分,经过4分钟两人相遇。相遇时李小军比王顺多走了( )米。
A.60 B.279 C.644
4.小文和小静一起到文具店买钢笔,小文买了5支钢笔,小静买了12支钢笔,小文比小静少花了84元。解:设每支钢笔x元,根据题意,可得x=( )。
A.12 B.7 C.16.8
5.甲乙两地间的铁路长480千米,客车和货车同时从两地相对开出,经过4小时相遇:已知客车每小时行65千米,货车每小时行x千米。不正确的方程是( )。
A. B. C.
6.无锡灵山大佛的高是88米,是四川乐山大佛的1.15倍还多0.6米,四川乐山大佛的高度是多少米?解:设乐山大佛高x米。下列方程式不正确的有( )。
A. B. C. D.
7.甲、乙两车同时从两地出发,相向而行。甲车每时行105千米,5时后两车在距中点30千米处相遇。若乙车慢一些,则乙车每时行( )千米。
A.93 B.99 C.111
8.甲、乙两人由相距60km的两地同时出发相向而行,甲步行每小时走5km,乙骑自行车,3h后两人相遇,则乙的速度为每小时( )。
A.5km B.10km C.15km D.20km
二、看图列式
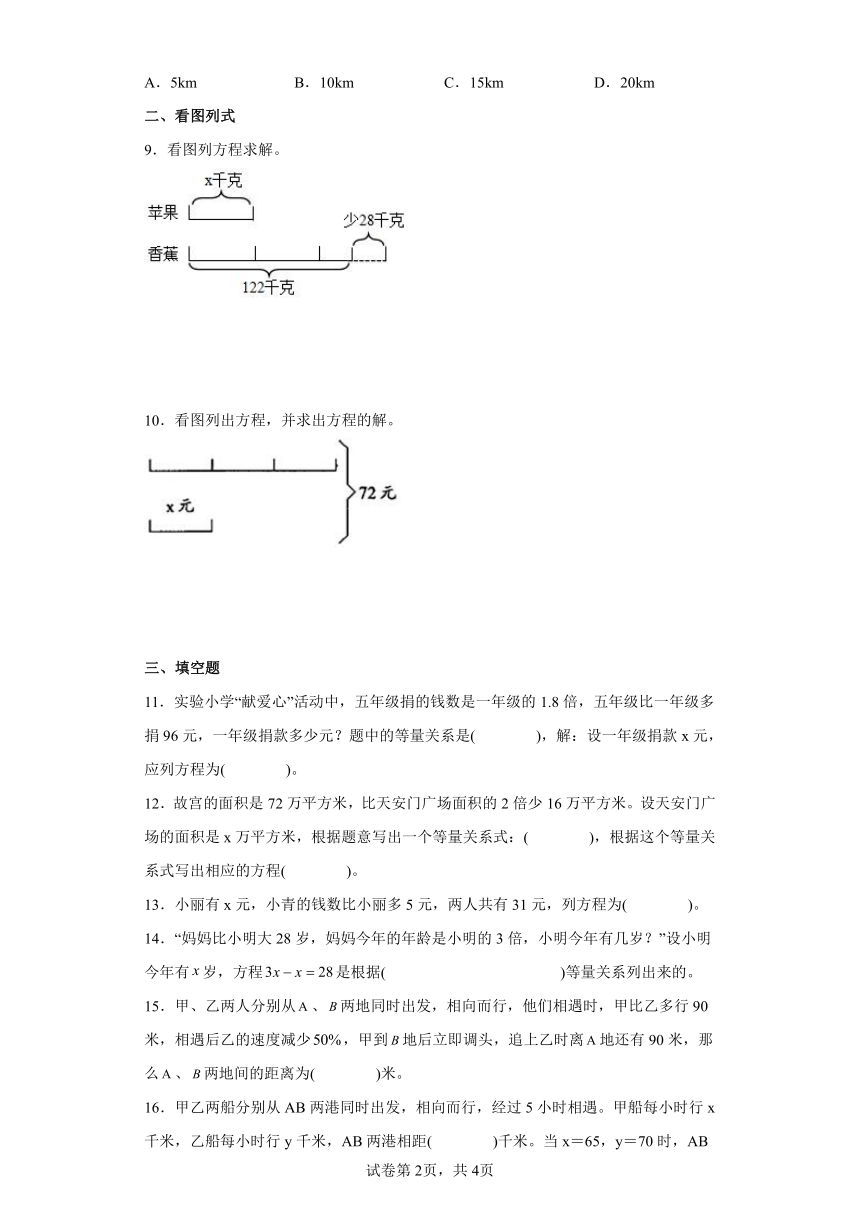
9.看图列方程求解。
10.看图列出方程,并求出方程的解。
三、填空题
11.实验小学“献爱心”活动中,五年级捐的钱数是一年级的1.8倍,五年级比一年级多捐96元,一年级捐款多少元?题中的等量关系是( ),解:设一年级捐款x元,应列方程为( )。
12.故宫的面积是72万平方米,比天安门广场面积的2倍少16万平方米。设天安门广场的面积是x万平方米,根据题意写出一个等量关系式:( ),根据这个等量关系式写出相应的方程( )。
13.小丽有x元,小青的钱数比小丽多5元,两人共有31元,列方程为( )。
14.“妈妈比小明大28岁,妈妈今年的年龄是小明的3倍,小明今年有几岁?”设小明今年有岁,方程是根据( )等量关系列出来的。
15.甲、乙两人分别从、两地同时出发,相向而行,他们相遇时,甲比乙多行90米,相遇后乙的速度减少,甲到地后立即调头,追上乙时离地还有90米,那么、两地间的距离为( )米。
16.甲乙两船分别从AB两港同时出发,相向而行,经过5小时相遇。甲船每小时行x千米,乙船每小时行y千米,AB两港相距( )千米。当x=65,y=70时,AB两港相距( )千米。
17.小明和小刚在广场四周跑步。小明跑一圈用6分钟,小刚跑一圈用9分钟。如果两人同时从同一地点出发,背向而行,至少( )分钟后两人相遇;如果两人同时从同一地点出发,同向而行,至少( )分钟后两人在起点相遇。
18.公交车从甲站到乙站每间隔5分钟一趟,全程走15分钟,某人骑自行车从乙站往甲站行走,开始时恰好遇见一辆公交车,行走过程中又遇见10辆,到甲站时又一辆公交车刚要出发,这人走了( )分钟。
四、判断题
19.将一张正方形纸对折两次,可能折出4个长方形,也可能折出4个小正方形,还可能折出4个三角形。( )
20.同学们参加“喜迎十四运”绘画展览,五年级一共去了264人,五年级去的人数比四年级的1.4倍少16人,设四年级去了x人,则可列方程为。( )
21.一长方形的长比宽的4倍多2厘米,长是14厘米,若设宽为x厘米,则列方程为4x+2=14。( )
22.用一张圆形纸对折再对折,折出来的一定是直角。( )
五、解答题
23.看图列方程,不用计算。
24.2022年冬奥会吉祥物冰墩墩是中国文化和奥林匹克精神又一次完美的结合。爸爸出差时买了3个冰墩墩福袋挂饰和4个冰墩墩旋转饰扣,共花了26元,其中冰墩墩福袋2元一个。一个冰墩墩旋转饰扣多少钱?(用方程解)
25.甲,乙两个工程队合修一条750米长的公路,同时各从一端修建,预计25天修好。甲队平均每天修16.5米,乙队平均每天修多少米?(列方程解答)
26.赵松林和李强都喜欢集邮,赵松林买了某纪念邮票20枚,李强买了8枚这种邮票,赵松林比李强多花了144元.每枚邮票多少元钱?(用方程解答)
27.北京到上海的公路全长约是1280千米,李叔叔和马叔叔驾车同时从北京和上海相对开出,8小时后相遇,李叔叔平均每小时行驶75千米,马叔叔平均每小时行驶多少千米?(列方程解答)
28.甲、乙两车同时从两地相对开出,已知甲车每小时行驶56.5千米,乙车每小时行驶64.5千米,且两车相遇时乙车比甲车多行驶44千米,则两车几小时相遇?
29.A、B两地相距1035千米,甲、乙两车分别从A、B两地同时出发,相向而行,5小时后两车相遇。甲车每小时的速度是乙车的1.3倍,甲、乙两车平均每小时分别行驶多少千米?(用方程解)
30.甲、乙两车同时从两地相对开出,两地相距480千米,4小时后相遇,甲的速度是乙的1.4倍,乙每小时行多少千米?(用方程解)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】
【分析】
根据题意,一条裙子的价格是一条裤子的3倍,设裤子的售价是x元,裙子的售价为3x元,裙子和裤子一共92元,列方程:3x+x=92,据此解答。
【详解】
解:设一条裙子的售价是x元。
3x+x=92
4x=92
x=92÷4
x=23
故答案为:C
【点睛】
根据方程的实际应用,利用裙子和裤子售价的关系,设出未知数,找出相关的量,列方程。
2.C
【解析】
【分析】
根据题意,设每套明信片x元,根据单价×数量=总价,小敏买15套的钱+小华买8套的钱=总钱数,列方程解答。
【详解】
解:设每套明信片x元,
15x+8x=368
23x=368
x=16
故答案为:C。
【点睛】
列方程解答应用题的关键是找出等量关系,根据等量关系列方程。
3.A
【解析】
【分析】
根据“速度差×相遇时间=路程差”代入数据解答即可。
【详解】
(米
故答案为:A
【点睛】
解答本题也可以根据“速度×时间=路程”分别求出王顺和李小军行走的路程,然后再作差即可。
4.A
【解析】
【分析】
由题意可知,(小静购买钢笔的只数-小文购买钢笔的只数)×钢笔的单价=小文比小静少花的钱数,据此解答。
【详解】
解:设每支钢笔x元。
(12-5)x=84
7x=84
x=84÷7
x=12
所以,每支钢笔12元。
故答案为:A
【点睛】
根据题意找出等量关系式并准确列方程求出方程的解是解答题目的关键。
5.A
【解析】
【分析】
根据题意,逐一判断三个选项中的方程所依据的等量关系,再判断这个等量关系是否符合题意,做出正确的选择。
【详解】
A.4x=480-65所依据的等量关系是:货车行的路程=甲乙两地之间的路程-客车的速度,不符合题意。
B.65+x=480÷4所依据的等量关系是:两车的速度和=甲乙两地之间的路程÷相遇时间,符合题意。
C.(65+x)×4=480所依据的等量关系是:两车的速度和×相遇时间=甲乙两地之间的路程,符合题意。
故答案为:A
【点睛】
本题考查列方程解应用题,解题关键是判断三个选项中的方程所依据的等量关系,再判断这个等量关系是否符合题意。
6.D
【解析】
【分析】
根据题意,设乐山大佛高x米;无锡灵山大佛的高是四川乐山大佛的1.15倍还多0.6米,即四川乐山大佛的高×1.15,再加上0.6米,等于无锡灵山大佛的高,由此逐项分析各选项,进行解答。
【详解】
A.四川乐山大佛的高度×1.15+0.6米=无锡灵山大佛的高;列方程:1.15x+0.6=88,原题干正确;
B.灵山大佛的高减去四川乐山大佛的高的1.15倍,等于0.6米;列方程:88-1.15x=0.6;原题干正确;
C.无锡灵山大佛的高减去0.6米,等于四川乐山大佛的高的1.15倍,列方程:88-0.6=1.15x;原题干正确;
D.四川乐山大佛的高的1.15倍-0.6米≠无锡灵山大佛的高,即1.15x-0.6≠88,原题干错误。
故答案为:D
【点睛】
根据方程的实际应用,利用无锡灵山大佛与四川乐山大佛高度之间的关系,进行解答。
7.A
【解析】
【分析】
根据题意可知,乙车慢一些,两车在距离中点30千米处相遇,说明甲车比乙车多行了两个30千米,设乙车每小时行驶x千米,5小时行驶5x千米,甲车5小时行驶105×5千米,用甲车行驶的距离-乙车行驶的距离=甲车比乙车多行的距离,列方程:105×5-5x=30×2,解方程,即可解答。
【详解】
解:设乙车每小时行x千米。
105×5-5x=30×2
525-5x=60
5x=525-60
5x=465
x=465÷5
x=93
故答案为:A
【点睛】
解答本题的关键明确,甲车与乙车相遇时甲车行驶的距离比乙车多两个30千米。
8.C
【解析】
【分析】
根据题意,设乙的速度为每小时xkm,甲步行每小时走5km,3小时走5×3km;乙每小时x千米,3小时行3xkm,甲走的距离+乙行驶的距离=两地的距离,列方程:5×3+3x=60,解方程,即可解答。
【详解】
解:设乙速度为每小时xkm。
5×3+3x=60
15+3x=60
3x=60-15
3x=45
x=45÷3
x=15
故答案为:C
【点睛】
利用速度、时间和距离三者关系,设出未知数,找出相关的量,列方程,解方程。
9.
【解析】
【分析】
通过线段图可以知道:苹果有x千克,香蕉的质量是苹果质量的3倍少28千克,即(3x-28)千克,是122千克。由此可知“苹果的质量×3-28=122”,据此列方程解答。
【详解】
解:
10.x=18
【解析】
【分析】
观察图形可知,一份是x元,三份是3x元,一共是72元,列方程:x+3x=72,解方程即可。
【详解】
x+3x=72
解:4x=72
x=72÷4
x=18
11. 五年级的捐款钱数-一年级的捐款钱数=96元 1.8x-x=96
【解析】
【分析】
分析题意可知,把一年级的捐款钱数设为未知数,五年级的捐款钱数=一年级的捐款钱数×1.8,等量关系式:五年级的捐款钱数-一年级的捐款钱数=96元。
【详解】
等量关系式:五年级的捐款钱数-一年级的捐款钱数=96元。
解:设一年级捐款x元,则五年级捐款1.8x元。
1.8x-x=96
0.8x=96
x=96÷0.8
x=120
所以,一年级捐款120元。
【点睛】
本题主要考查用方程解决实际问题,找出等量关系式是列方程解答题目的关键。
12. 天安门广场的面积×2-16=故宫的面积 2x-16=72
【解析】
【分析】
根据故宫的面积比天安门广场面积的2倍少16万平方米得等量关系式:天安门广场的面积×2-16=故宫的面积,设天安门广场的面积是x万平方米,代入数据列方程解答。
【详解】
由分析得,
根据题意写出一个等量关系式:天安门广场的面积×2-16=故宫的面积
解:设天安门广场的面积是x万平方米,根据题意得
2x-16=72
2x=72+16
2x=88
x=44
则天安门广场的面积是44万平方米。
【点睛】
此题考查的是列方程解决问题,理解题意明确等量关系是解题关键。
13.x+x+5=31
【解析】
【分析】
根据题意,用含有x的式子表示出小青,然后两人相加等于31元,以此列式。
【详解】
小丽:x元;
小青:x+5;
总钱数:x+x+5=31
【点睛】
此题主要考查学生设未知数列方程的能力。
14.妈妈今年的岁数-小明今年的岁数岁
【解析】
【分析】
由题可知,小明今年的年龄是岁,则妈妈今年的年龄是3岁;是根据妈妈比小明大28岁,即:妈妈今年的岁数-小明今年的岁数=28岁。
【详解】
由分析可知:方程是根据“妈妈今年的岁数-小明今年的岁数=28岁”等量关系列出来的。
【点睛】
解答本题的关键是根据题意找出等量关系,同时要注意年龄问题中年龄差是不变的。
15.450
【解析】
【分析】
设甲、乙第一次相遇时乙的走了x米,甲比乙多行90米,则甲走了(x+90)米;由此可知,A、B两地之间的距离为(2x+90)米;第二次相遇时,距离A地还有90米,则乙在第一次到第二次相遇的时间又走了[(2x+90)-90-x]=x米;即两段时间内乙走了相同的距离,都是x米;因为第二段时间内的速度减少50%,因此第二段时间是第一段时间的两倍;甲第二段时间走了(x+2x)米,第一段时间走了(x+90)米,又因为甲的速度没有变,所以3x=2×(x+90),求出x的值,进而求出A、B之间的距离。
【详解】
解:设甲、乙第一次相遇时乙走了x米,则此时甲走了(x+90)米,A、B两地的距离为(2x+90)米。
x+1÷50%x=2×(x+90)
3x=2x+180
x=180
180×2+90
=360+90
=450(米)
【点睛】
解答本题的关键是清楚乙走的路程,设出未知数,找出相关的量,列方程,解方程。
16. 5x+5y 675
【解析】
【分析】
根据相遇问题公式:路程=速度和×时间,可知AB两港相距(x+y)×5=5x+5y千米,当x=65,y=70时,代入计算即可。
【详解】
(x+y)×5=5x+5y千米
当x=65,y=70时
5x+5y
=5×65+5×70
=675(千米)
【点睛】
此题考查了相遇问题的解决方法,要熟练掌握。
17. 3.6 18
【解析】
【分析】
把一圈的路程看成单位“1”,小明的速度是1÷6,小刚的速度是1÷9,如果两人从同一地点出发,背向而行,相遇时两人正好跑了1圈,用1除以两人的速度和,即可求出相遇时间;如果两人同时从同一地点出发,同向而行,如果两人再次在起点相遇,那么两人用的时间应是6和9的最小公倍数,由此求解。
【详解】
背向而行相遇时间:1÷6=,1÷9=
(分钟);
因为:6的倍数有:6、12、18、24
9的倍数有:9、18、27、36
6和9的最小公倍数是18。
所以:同向而行,至少18分钟后两人在起点相遇。
【点睛】
问题2也可以看成追及问题,两人在第一次起点相遇时,是小明第一次追上小刚,那么小明比小刚多跑一圈,用1除以两人的速度差即可求解。
18.40
【解析】
【分析】
公交车全程走15分钟,每间隔5分钟发一趟车,他出发时,正好一辆公交车到站。由此可知,15÷5=3,路上有3-1=2(辆)公交车,且甲站有1辆公交车要发车。根据题意,只要求出从他出发开始,一共发了多少辆车即可求出他骑行了多少时间。他全程一共遇见了10辆,减去他出发时已经在路上的2辆,即一共发车了8辆。
【详解】
据分析:他出发时路上有:(15÷5)-1
=3-1
=2(辆)
他从出发到甲站,要经过:
5×(10-2)
=5×8
=40(分钟)
【点睛】
此题属于多次相遇问题,考查学生分析问题的能力,可以画线段图来便于理解。
19.√
【解析】
略
20.√
【解析】
【分析】
根据题目可知,五年级去的人数比四年级的1.4倍少16人,则五年级去的人数=四年级去的人数×1.4-16;把x和五年级的人数代入等式,即可列式。
【详解】
根据分析可知,1.4x-16=264
故答案为:√。
【点睛】
本题主要考查列方程,准确找到等量的关系。
21.√
【解析】
【分析】
设宽为x厘米,根据等量关系式:宽×4倍+2厘米=长,列方程判断即可。
【详解】
解:设宽为x厘米,
4x+2=14
4x=12
x=3
答:宽为3厘米。
故答案为:√。
【点睛】
列方程解应用题,关键是列出已知条件和未知条件之间的等量关系式。
22.√
【解析】
【分析】
一张圆形纸对折,折出来的角是以圆心为顶点,两半径为边的平角,再对折,折出来的角是以圆心为顶点,半径为边的直角,据此解答。
【详解】
根据分析可知,用一张圆形纸对折再对折,折出来的一定是直角。
原题干说的正确。
故答案为:√
【点睛】
本题考查简单图形的折叠问题,直角的意义;此题可以动手操作一下,很简单。
23.x+x=280
【解析】
【分析】
看图可知,桌子价钱是单位“1”,桌子价钱×椅子对应分率=椅子价钱,根据桌子价钱+椅子价钱=280元,列出方程即可。
【详解】
根据分析,列方程为:x+x=280
【点睛】
关键是看懂图意,用方程解决问题的关键是找到等量关系。
24.5元
【解析】
【分析】
根据“3个冰墩墩福袋挂饰和4个冰墩墩旋转饰扣,共花了26元”,可以提炼出这道题的等量关系是:1个冰墩墩福袋挂饰的钱数×3+1个冰墩墩旋转饰扣的钱数×4=26元,根据这个等量关系列出方程,再依据等式的性质解答。
【详解】
解:设一个冰墩墩旋转饰扣元。
答:一个冰墩墩旋转饰扣5元。
【点睛】
本题主要考查列方程解应用题,找准题目中的等量关系是解答此题的关键。
25.13.5米
【解析】
【分析】
先找出等量关系:甲队平均每天修的长度×天数+乙队平均每天修的长度×天数=这条公路的长度,再设乙队平均每天修x米,然后根据等量关系列方程求解。
【详解】
解:设乙队平均每天修x米。
16.5×25+25x=750
412.5+25x=750
25x=750-412.5
25x=337.5
x=337.5÷25
x=13.5
答:乙队平均每天修13.5米。
【点睛】
此题考查了列方程解决实际问题,注意先根据题意找出等量关系。
26.12元
【解析】
【详解】
解:设每枚邮票x元钱.
20x-8x=144
x=12
答:每枚邮票12元钱.
27.85千米
【解析】
【分析】
根据题意,设马叔叔平均每小时行驶x千米,李叔叔每小时行驶75千米,8小时行驶75×8千米;马叔叔平均每小时行驶x千米,8时行驶8x千米,李叔叔行驶的距离+马叔叔行驶的距离=北京到上海的公路全长,列方程:75×8+8x=1280,解方程,即可解答。
【详解】
解:设马叔叔平均每小时行驶x千米。
75×8+8x=1280
600+8x=1280
8x=1280-600
8x=680
x=680÷8
x=85
答:马叔叔平均每小时行驶85千米。
【点睛】
利用方程的实际应用,根据距离、速度和时间三者的关系,设出未知数,找出相关的量,列方程,解方程。
28.5.5小时
【解析】
【分析】
乙车每小时比甲车多行驶(64.5-56.5)千米,因为两车相遇时乙车比甲车多行驶44千米,所以用多行驶的路程除以每小时多行驶的路程即可求得相遇时间。
【详解】
(小时)
答:两车5.5小时相遇。
【点睛】
解决本题的关键是根据路程差÷速度差=时间,求出两车的相遇时间。
29.甲车117千米;乙车90千米
【解析】
【分析】
甲车的速度=乙车的速度×1.3,等量关系式:(甲车的速度+乙车的速度)×相遇时间=A、B两地之间的总路程,据此解答。
【详解】
解:设乙车平均每小时行驶x千米,则甲车平均每小时行驶1.3x千米。
(1.3x+x)×5=1035
2.3x×5=1035
11.5x=1035
11.5x÷11.5=1035÷11.5
x=90
甲:1.3×90=117(千米)
答:甲车平均每小时行驶117千米,乙车平均每小时行驶90千米。
【点睛】
分析题意找出等量关系式是解答题目的关键。
30.50千米
【解析】
【分析】
根据题意,设乙每小时行x千米,甲的速度是乙的1.4倍,则甲每小时行1.4x千米;4小时两车相遇,甲车行的距离是1.4x×4千米;乙车行的距离是4x千米,两车行的距离和是两地的距离,列方程:1.4x×4+4x=480,解方程,即可解答。
【详解】
解:设乙每小时行x千米,则甲每小时行1.4x千米。
1.4x×4+4x=480
5.6x+4x=480
9.6x=480
x=480÷9.6
x=50
答:乙车每小时行50千米。
【点睛】
根据方程的实际应用,由于两车相遇等于两地的距离,利用速度、时间和距离,设出未知数,找出先关的量,列方程,解方程。
答案第1页,共2页
答案第1页,共2页
第七单元 用方程解问题
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 五 总分
得分
一、选择题
1.一条裙子和一条裤子共92元,一条裙子的价格是一条裤子的3倍,设一条裤子的售价是元,根据这些条件,列出的方程正确的是( )。
A. B. C.
2.小敏和小华买同样的冬奥会明信片,小敏买了15套,小华买了8套,小敏和小华一共花了368元,求每套明信片多少元。解:设每套明信片x元,下列方程正确的是( )。
A. B. C.
3.王顺和李小军同时从两地沿一条公路面对面走来。王顺的速度是73米分,李小军的速度是88米分,经过4分钟两人相遇。相遇时李小军比王顺多走了( )米。
A.60 B.279 C.644
4.小文和小静一起到文具店买钢笔,小文买了5支钢笔,小静买了12支钢笔,小文比小静少花了84元。解:设每支钢笔x元,根据题意,可得x=( )。
A.12 B.7 C.16.8
5.甲乙两地间的铁路长480千米,客车和货车同时从两地相对开出,经过4小时相遇:已知客车每小时行65千米,货车每小时行x千米。不正确的方程是( )。
A. B. C.
6.无锡灵山大佛的高是88米,是四川乐山大佛的1.15倍还多0.6米,四川乐山大佛的高度是多少米?解:设乐山大佛高x米。下列方程式不正确的有( )。
A. B. C. D.
7.甲、乙两车同时从两地出发,相向而行。甲车每时行105千米,5时后两车在距中点30千米处相遇。若乙车慢一些,则乙车每时行( )千米。
A.93 B.99 C.111
8.甲、乙两人由相距60km的两地同时出发相向而行,甲步行每小时走5km,乙骑自行车,3h后两人相遇,则乙的速度为每小时( )。
A.5km B.10km C.15km D.20km
二、看图列式
9.看图列方程求解。
10.看图列出方程,并求出方程的解。
三、填空题
11.实验小学“献爱心”活动中,五年级捐的钱数是一年级的1.8倍,五年级比一年级多捐96元,一年级捐款多少元?题中的等量关系是( ),解:设一年级捐款x元,应列方程为( )。
12.故宫的面积是72万平方米,比天安门广场面积的2倍少16万平方米。设天安门广场的面积是x万平方米,根据题意写出一个等量关系式:( ),根据这个等量关系式写出相应的方程( )。
13.小丽有x元,小青的钱数比小丽多5元,两人共有31元,列方程为( )。
14.“妈妈比小明大28岁,妈妈今年的年龄是小明的3倍,小明今年有几岁?”设小明今年有岁,方程是根据( )等量关系列出来的。
15.甲、乙两人分别从、两地同时出发,相向而行,他们相遇时,甲比乙多行90米,相遇后乙的速度减少,甲到地后立即调头,追上乙时离地还有90米,那么、两地间的距离为( )米。
16.甲乙两船分别从AB两港同时出发,相向而行,经过5小时相遇。甲船每小时行x千米,乙船每小时行y千米,AB两港相距( )千米。当x=65,y=70时,AB两港相距( )千米。
17.小明和小刚在广场四周跑步。小明跑一圈用6分钟,小刚跑一圈用9分钟。如果两人同时从同一地点出发,背向而行,至少( )分钟后两人相遇;如果两人同时从同一地点出发,同向而行,至少( )分钟后两人在起点相遇。
18.公交车从甲站到乙站每间隔5分钟一趟,全程走15分钟,某人骑自行车从乙站往甲站行走,开始时恰好遇见一辆公交车,行走过程中又遇见10辆,到甲站时又一辆公交车刚要出发,这人走了( )分钟。
四、判断题
19.将一张正方形纸对折两次,可能折出4个长方形,也可能折出4个小正方形,还可能折出4个三角形。( )
20.同学们参加“喜迎十四运”绘画展览,五年级一共去了264人,五年级去的人数比四年级的1.4倍少16人,设四年级去了x人,则可列方程为。( )
21.一长方形的长比宽的4倍多2厘米,长是14厘米,若设宽为x厘米,则列方程为4x+2=14。( )
22.用一张圆形纸对折再对折,折出来的一定是直角。( )
五、解答题
23.看图列方程,不用计算。
24.2022年冬奥会吉祥物冰墩墩是中国文化和奥林匹克精神又一次完美的结合。爸爸出差时买了3个冰墩墩福袋挂饰和4个冰墩墩旋转饰扣,共花了26元,其中冰墩墩福袋2元一个。一个冰墩墩旋转饰扣多少钱?(用方程解)
25.甲,乙两个工程队合修一条750米长的公路,同时各从一端修建,预计25天修好。甲队平均每天修16.5米,乙队平均每天修多少米?(列方程解答)
26.赵松林和李强都喜欢集邮,赵松林买了某纪念邮票20枚,李强买了8枚这种邮票,赵松林比李强多花了144元.每枚邮票多少元钱?(用方程解答)
27.北京到上海的公路全长约是1280千米,李叔叔和马叔叔驾车同时从北京和上海相对开出,8小时后相遇,李叔叔平均每小时行驶75千米,马叔叔平均每小时行驶多少千米?(列方程解答)
28.甲、乙两车同时从两地相对开出,已知甲车每小时行驶56.5千米,乙车每小时行驶64.5千米,且两车相遇时乙车比甲车多行驶44千米,则两车几小时相遇?
29.A、B两地相距1035千米,甲、乙两车分别从A、B两地同时出发,相向而行,5小时后两车相遇。甲车每小时的速度是乙车的1.3倍,甲、乙两车平均每小时分别行驶多少千米?(用方程解)
30.甲、乙两车同时从两地相对开出,两地相距480千米,4小时后相遇,甲的速度是乙的1.4倍,乙每小时行多少千米?(用方程解)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】
【分析】
根据题意,一条裙子的价格是一条裤子的3倍,设裤子的售价是x元,裙子的售价为3x元,裙子和裤子一共92元,列方程:3x+x=92,据此解答。
【详解】
解:设一条裙子的售价是x元。
3x+x=92
4x=92
x=92÷4
x=23
故答案为:C
【点睛】
根据方程的实际应用,利用裙子和裤子售价的关系,设出未知数,找出相关的量,列方程。
2.C
【解析】
【分析】
根据题意,设每套明信片x元,根据单价×数量=总价,小敏买15套的钱+小华买8套的钱=总钱数,列方程解答。
【详解】
解:设每套明信片x元,
15x+8x=368
23x=368
x=16
故答案为:C。
【点睛】
列方程解答应用题的关键是找出等量关系,根据等量关系列方程。
3.A
【解析】
【分析】
根据“速度差×相遇时间=路程差”代入数据解答即可。
【详解】
(米
故答案为:A
【点睛】
解答本题也可以根据“速度×时间=路程”分别求出王顺和李小军行走的路程,然后再作差即可。
4.A
【解析】
【分析】
由题意可知,(小静购买钢笔的只数-小文购买钢笔的只数)×钢笔的单价=小文比小静少花的钱数,据此解答。
【详解】
解:设每支钢笔x元。
(12-5)x=84
7x=84
x=84÷7
x=12
所以,每支钢笔12元。
故答案为:A
【点睛】
根据题意找出等量关系式并准确列方程求出方程的解是解答题目的关键。
5.A
【解析】
【分析】
根据题意,逐一判断三个选项中的方程所依据的等量关系,再判断这个等量关系是否符合题意,做出正确的选择。
【详解】
A.4x=480-65所依据的等量关系是:货车行的路程=甲乙两地之间的路程-客车的速度,不符合题意。
B.65+x=480÷4所依据的等量关系是:两车的速度和=甲乙两地之间的路程÷相遇时间,符合题意。
C.(65+x)×4=480所依据的等量关系是:两车的速度和×相遇时间=甲乙两地之间的路程,符合题意。
故答案为:A
【点睛】
本题考查列方程解应用题,解题关键是判断三个选项中的方程所依据的等量关系,再判断这个等量关系是否符合题意。
6.D
【解析】
【分析】
根据题意,设乐山大佛高x米;无锡灵山大佛的高是四川乐山大佛的1.15倍还多0.6米,即四川乐山大佛的高×1.15,再加上0.6米,等于无锡灵山大佛的高,由此逐项分析各选项,进行解答。
【详解】
A.四川乐山大佛的高度×1.15+0.6米=无锡灵山大佛的高;列方程:1.15x+0.6=88,原题干正确;
B.灵山大佛的高减去四川乐山大佛的高的1.15倍,等于0.6米;列方程:88-1.15x=0.6;原题干正确;
C.无锡灵山大佛的高减去0.6米,等于四川乐山大佛的高的1.15倍,列方程:88-0.6=1.15x;原题干正确;
D.四川乐山大佛的高的1.15倍-0.6米≠无锡灵山大佛的高,即1.15x-0.6≠88,原题干错误。
故答案为:D
【点睛】
根据方程的实际应用,利用无锡灵山大佛与四川乐山大佛高度之间的关系,进行解答。
7.A
【解析】
【分析】
根据题意可知,乙车慢一些,两车在距离中点30千米处相遇,说明甲车比乙车多行了两个30千米,设乙车每小时行驶x千米,5小时行驶5x千米,甲车5小时行驶105×5千米,用甲车行驶的距离-乙车行驶的距离=甲车比乙车多行的距离,列方程:105×5-5x=30×2,解方程,即可解答。
【详解】
解:设乙车每小时行x千米。
105×5-5x=30×2
525-5x=60
5x=525-60
5x=465
x=465÷5
x=93
故答案为:A
【点睛】
解答本题的关键明确,甲车与乙车相遇时甲车行驶的距离比乙车多两个30千米。
8.C
【解析】
【分析】
根据题意,设乙的速度为每小时xkm,甲步行每小时走5km,3小时走5×3km;乙每小时x千米,3小时行3xkm,甲走的距离+乙行驶的距离=两地的距离,列方程:5×3+3x=60,解方程,即可解答。
【详解】
解:设乙速度为每小时xkm。
5×3+3x=60
15+3x=60
3x=60-15
3x=45
x=45÷3
x=15
故答案为:C
【点睛】
利用速度、时间和距离三者关系,设出未知数,找出相关的量,列方程,解方程。
9.
【解析】
【分析】
通过线段图可以知道:苹果有x千克,香蕉的质量是苹果质量的3倍少28千克,即(3x-28)千克,是122千克。由此可知“苹果的质量×3-28=122”,据此列方程解答。
【详解】
解:
10.x=18
【解析】
【分析】
观察图形可知,一份是x元,三份是3x元,一共是72元,列方程:x+3x=72,解方程即可。
【详解】
x+3x=72
解:4x=72
x=72÷4
x=18
11. 五年级的捐款钱数-一年级的捐款钱数=96元 1.8x-x=96
【解析】
【分析】
分析题意可知,把一年级的捐款钱数设为未知数,五年级的捐款钱数=一年级的捐款钱数×1.8,等量关系式:五年级的捐款钱数-一年级的捐款钱数=96元。
【详解】
等量关系式:五年级的捐款钱数-一年级的捐款钱数=96元。
解:设一年级捐款x元,则五年级捐款1.8x元。
1.8x-x=96
0.8x=96
x=96÷0.8
x=120
所以,一年级捐款120元。
【点睛】
本题主要考查用方程解决实际问题,找出等量关系式是列方程解答题目的关键。
12. 天安门广场的面积×2-16=故宫的面积 2x-16=72
【解析】
【分析】
根据故宫的面积比天安门广场面积的2倍少16万平方米得等量关系式:天安门广场的面积×2-16=故宫的面积,设天安门广场的面积是x万平方米,代入数据列方程解答。
【详解】
由分析得,
根据题意写出一个等量关系式:天安门广场的面积×2-16=故宫的面积
解:设天安门广场的面积是x万平方米,根据题意得
2x-16=72
2x=72+16
2x=88
x=44
则天安门广场的面积是44万平方米。
【点睛】
此题考查的是列方程解决问题,理解题意明确等量关系是解题关键。
13.x+x+5=31
【解析】
【分析】
根据题意,用含有x的式子表示出小青,然后两人相加等于31元,以此列式。
【详解】
小丽:x元;
小青:x+5;
总钱数:x+x+5=31
【点睛】
此题主要考查学生设未知数列方程的能力。
14.妈妈今年的岁数-小明今年的岁数岁
【解析】
【分析】
由题可知,小明今年的年龄是岁,则妈妈今年的年龄是3岁;是根据妈妈比小明大28岁,即:妈妈今年的岁数-小明今年的岁数=28岁。
【详解】
由分析可知:方程是根据“妈妈今年的岁数-小明今年的岁数=28岁”等量关系列出来的。
【点睛】
解答本题的关键是根据题意找出等量关系,同时要注意年龄问题中年龄差是不变的。
15.450
【解析】
【分析】
设甲、乙第一次相遇时乙的走了x米,甲比乙多行90米,则甲走了(x+90)米;由此可知,A、B两地之间的距离为(2x+90)米;第二次相遇时,距离A地还有90米,则乙在第一次到第二次相遇的时间又走了[(2x+90)-90-x]=x米;即两段时间内乙走了相同的距离,都是x米;因为第二段时间内的速度减少50%,因此第二段时间是第一段时间的两倍;甲第二段时间走了(x+2x)米,第一段时间走了(x+90)米,又因为甲的速度没有变,所以3x=2×(x+90),求出x的值,进而求出A、B之间的距离。
【详解】
解:设甲、乙第一次相遇时乙走了x米,则此时甲走了(x+90)米,A、B两地的距离为(2x+90)米。
x+1÷50%x=2×(x+90)
3x=2x+180
x=180
180×2+90
=360+90
=450(米)
【点睛】
解答本题的关键是清楚乙走的路程,设出未知数,找出相关的量,列方程,解方程。
16. 5x+5y 675
【解析】
【分析】
根据相遇问题公式:路程=速度和×时间,可知AB两港相距(x+y)×5=5x+5y千米,当x=65,y=70时,代入计算即可。
【详解】
(x+y)×5=5x+5y千米
当x=65,y=70时
5x+5y
=5×65+5×70
=675(千米)
【点睛】
此题考查了相遇问题的解决方法,要熟练掌握。
17. 3.6 18
【解析】
【分析】
把一圈的路程看成单位“1”,小明的速度是1÷6,小刚的速度是1÷9,如果两人从同一地点出发,背向而行,相遇时两人正好跑了1圈,用1除以两人的速度和,即可求出相遇时间;如果两人同时从同一地点出发,同向而行,如果两人再次在起点相遇,那么两人用的时间应是6和9的最小公倍数,由此求解。
【详解】
背向而行相遇时间:1÷6=,1÷9=
(分钟);
因为:6的倍数有:6、12、18、24
9的倍数有:9、18、27、36
6和9的最小公倍数是18。
所以:同向而行,至少18分钟后两人在起点相遇。
【点睛】
问题2也可以看成追及问题,两人在第一次起点相遇时,是小明第一次追上小刚,那么小明比小刚多跑一圈,用1除以两人的速度差即可求解。
18.40
【解析】
【分析】
公交车全程走15分钟,每间隔5分钟发一趟车,他出发时,正好一辆公交车到站。由此可知,15÷5=3,路上有3-1=2(辆)公交车,且甲站有1辆公交车要发车。根据题意,只要求出从他出发开始,一共发了多少辆车即可求出他骑行了多少时间。他全程一共遇见了10辆,减去他出发时已经在路上的2辆,即一共发车了8辆。
【详解】
据分析:他出发时路上有:(15÷5)-1
=3-1
=2(辆)
他从出发到甲站,要经过:
5×(10-2)
=5×8
=40(分钟)
【点睛】
此题属于多次相遇问题,考查学生分析问题的能力,可以画线段图来便于理解。
19.√
【解析】
略
20.√
【解析】
【分析】
根据题目可知,五年级去的人数比四年级的1.4倍少16人,则五年级去的人数=四年级去的人数×1.4-16;把x和五年级的人数代入等式,即可列式。
【详解】
根据分析可知,1.4x-16=264
故答案为:√。
【点睛】
本题主要考查列方程,准确找到等量的关系。
21.√
【解析】
【分析】
设宽为x厘米,根据等量关系式:宽×4倍+2厘米=长,列方程判断即可。
【详解】
解:设宽为x厘米,
4x+2=14
4x=12
x=3
答:宽为3厘米。
故答案为:√。
【点睛】
列方程解应用题,关键是列出已知条件和未知条件之间的等量关系式。
22.√
【解析】
【分析】
一张圆形纸对折,折出来的角是以圆心为顶点,两半径为边的平角,再对折,折出来的角是以圆心为顶点,半径为边的直角,据此解答。
【详解】
根据分析可知,用一张圆形纸对折再对折,折出来的一定是直角。
原题干说的正确。
故答案为:√
【点睛】
本题考查简单图形的折叠问题,直角的意义;此题可以动手操作一下,很简单。
23.x+x=280
【解析】
【分析】
看图可知,桌子价钱是单位“1”,桌子价钱×椅子对应分率=椅子价钱,根据桌子价钱+椅子价钱=280元,列出方程即可。
【详解】
根据分析,列方程为:x+x=280
【点睛】
关键是看懂图意,用方程解决问题的关键是找到等量关系。
24.5元
【解析】
【分析】
根据“3个冰墩墩福袋挂饰和4个冰墩墩旋转饰扣,共花了26元”,可以提炼出这道题的等量关系是:1个冰墩墩福袋挂饰的钱数×3+1个冰墩墩旋转饰扣的钱数×4=26元,根据这个等量关系列出方程,再依据等式的性质解答。
【详解】
解:设一个冰墩墩旋转饰扣元。
答:一个冰墩墩旋转饰扣5元。
【点睛】
本题主要考查列方程解应用题,找准题目中的等量关系是解答此题的关键。
25.13.5米
【解析】
【分析】
先找出等量关系:甲队平均每天修的长度×天数+乙队平均每天修的长度×天数=这条公路的长度,再设乙队平均每天修x米,然后根据等量关系列方程求解。
【详解】
解:设乙队平均每天修x米。
16.5×25+25x=750
412.5+25x=750
25x=750-412.5
25x=337.5
x=337.5÷25
x=13.5
答:乙队平均每天修13.5米。
【点睛】
此题考查了列方程解决实际问题,注意先根据题意找出等量关系。
26.12元
【解析】
【详解】
解:设每枚邮票x元钱.
20x-8x=144
x=12
答:每枚邮票12元钱.
27.85千米
【解析】
【分析】
根据题意,设马叔叔平均每小时行驶x千米,李叔叔每小时行驶75千米,8小时行驶75×8千米;马叔叔平均每小时行驶x千米,8时行驶8x千米,李叔叔行驶的距离+马叔叔行驶的距离=北京到上海的公路全长,列方程:75×8+8x=1280,解方程,即可解答。
【详解】
解:设马叔叔平均每小时行驶x千米。
75×8+8x=1280
600+8x=1280
8x=1280-600
8x=680
x=680÷8
x=85
答:马叔叔平均每小时行驶85千米。
【点睛】
利用方程的实际应用,根据距离、速度和时间三者的关系,设出未知数,找出相关的量,列方程,解方程。
28.5.5小时
【解析】
【分析】
乙车每小时比甲车多行驶(64.5-56.5)千米,因为两车相遇时乙车比甲车多行驶44千米,所以用多行驶的路程除以每小时多行驶的路程即可求得相遇时间。
【详解】
(小时)
答:两车5.5小时相遇。
【点睛】
解决本题的关键是根据路程差÷速度差=时间,求出两车的相遇时间。
29.甲车117千米;乙车90千米
【解析】
【分析】
甲车的速度=乙车的速度×1.3,等量关系式:(甲车的速度+乙车的速度)×相遇时间=A、B两地之间的总路程,据此解答。
【详解】
解:设乙车平均每小时行驶x千米,则甲车平均每小时行驶1.3x千米。
(1.3x+x)×5=1035
2.3x×5=1035
11.5x=1035
11.5x÷11.5=1035÷11.5
x=90
甲:1.3×90=117(千米)
答:甲车平均每小时行驶117千米,乙车平均每小时行驶90千米。
【点睛】
分析题意找出等量关系式是解答题目的关键。
30.50千米
【解析】
【分析】
根据题意,设乙每小时行x千米,甲的速度是乙的1.4倍,则甲每小时行1.4x千米;4小时两车相遇,甲车行的距离是1.4x×4千米;乙车行的距离是4x千米,两车行的距离和是两地的距离,列方程:1.4x×4+4x=480,解方程,即可解答。
【详解】
解:设乙每小时行x千米,则甲每小时行1.4x千米。
1.4x×4+4x=480
5.6x+4x=480
9.6x=480
x=480÷9.6
x=50
答:乙车每小时行50千米。
【点睛】
根据方程的实际应用,由于两车相遇等于两地的距离,利用速度、时间和距离,设出未知数,找出先关的量,列方程,解方程。
答案第1页,共2页
答案第1页,共2页
