北师大版(新)九上-1.1 菱形的性质与判定 第一课时【优质课件】
文档属性
| 名称 | 北师大版(新)九上-1.1 菱形的性质与判定 第一课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览









文档简介
(共37张PPT)
1.1 菱形的性质与判定
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
下面几幅图片中都含有一些平行四边形.观察这些平行四边形,你能发现它们有什么样的共同特征?
新课精讲
探索新知
1
知识点
菱形的定义
菱形的定义:有一组邻边相等的平行四边形叫做菱形.
要点精析:
(1)菱形必须满足两个条件:一是平行四边形;二是一组邻边相等.二者必须同时具备,缺一不可.
(2)菱形的定义既是菱形的基本性质,也是菱形的基本判定方法.
典题精讲
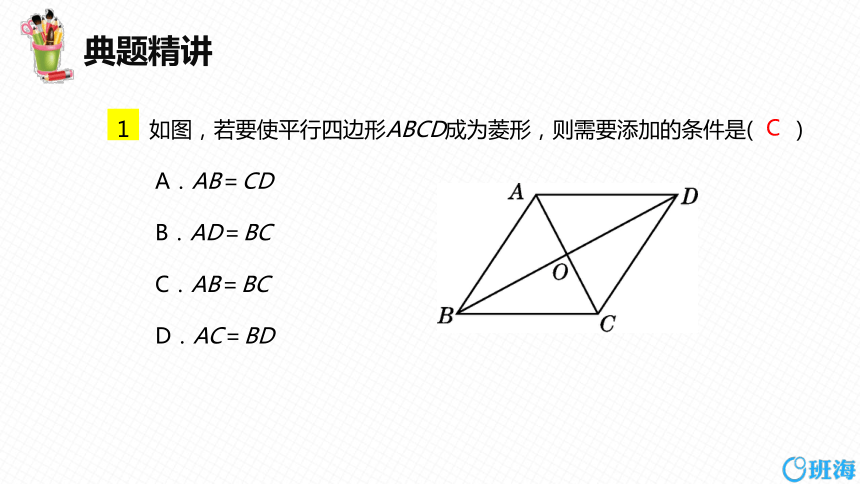
如图,若要使平行四边形ABCD成为菱形,则需要添加的条件是( )
A.AB=CD
B.AD=BC
C.AB=BC
D.AC=BD
C
典题精讲
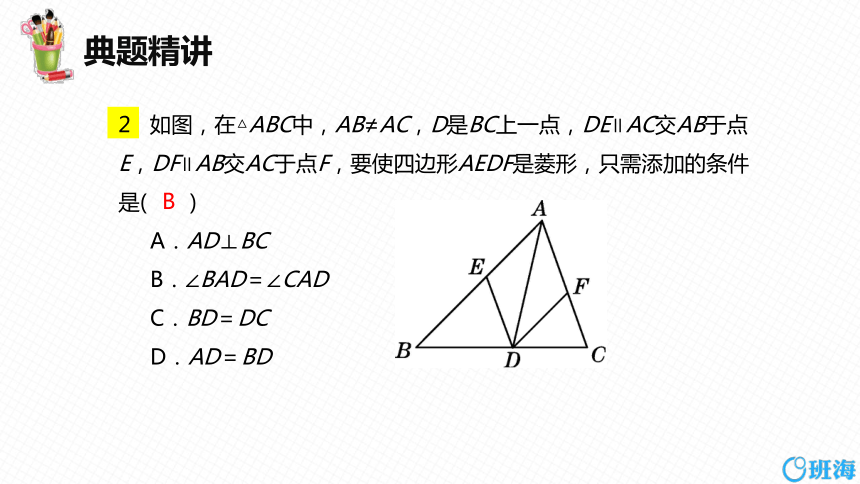
2 如图,在△ABC中,AB≠AC,D是BC上一点,DE∥AC交AB于点E,DF∥AB交AC于点F,要使四边形AEDF是菱形,只需添加的条件是( )
A.AD⊥BC
B.∠BAD=∠CAD
C.BD=DC
D.AD=BD
B
探索新知
2
知识点
菱形边的性质
菱形具有平行四边形的所有性质.此外,菱形还具有哪些特殊性质呢 根据菱形的轴对称性,你发现菱形的四条边具有什么大小关系
问 题
菱形的四条边都相等.
探索新知
例1 如图所示,菱形ABCD中,∠B=60°,AB=2,E、F分别是BC、CD的中点,连接AE、EF、AF,则△AEF的周长为( )
A. B.
C. D.3
分析:在菱形ABCD中,因为∠B=60°,连接AC,则△ABC是等边三角形,又因为E分别是BC的中点,所以AE垂直于BC,因此AE= ,所以△AEF的周长为 ,故选B.
B
探索新知
总 结
在菱形中作辅助线经常连接对角线,构造
三角形来做题,能够迎刃而解.
典题精讲
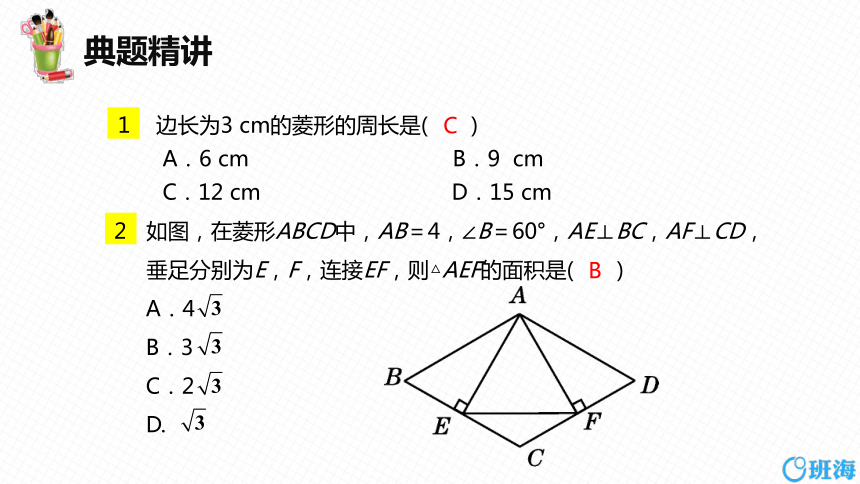
1 边长为3 cm的菱形的周长是( )
A.6 cm B.9 cm
C.12 cm D.15 cm
C
如图,在菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则△AEF的面积是( )
A.4
B.3
C.2
D.
B
探索新知
3
知识点
菱形对角线的性质
因为菱形是平行四边形,所以它具有平行四边形的所有性质.由于它的一组邻边相等,它是否具有一般平行四边形不具有的一些特殊性质呢?
思考
菱形的两条对角线AC与BD之间具有什么位置关系
探索新知
已知:如图,在菱形ABCD中,AB=AD,对角线AC与BD相交于点O.求证(1)AB=BC=CD=AD,(2)AC⊥BD.
证明:
(1)∵四边形ABCD是菱形,
∴AB=CD,AD=BC(菱形的对边相等).
又∵AB=AD,∴AB=BC=CD=AD.
(2)∵AB=AD,∴△ABD是等腰三角形.
又∵四边形ABCD是菱形,∴OB=OD(菱形的对角线互相平分).
在等腰三角形ABD中,∵OB=OD,∴AO⊥BD,
即 AC⊥BD.
探索新知
归 纳
定理 菱形的对角线互相垂直.
探索新知
问 题
菱形的面积如何计算呢?
菱形的面积有两种计算方法:
一种是底乘以高的积;
另一种是对角线乘积的一半.所以在求菱形的面积时,要灵活运用使计算简单.
探索新知
例2 如图,在菱形ABCD中,对角线AC与BD相交于
点O,BD=12 cm,AC=6 cm.求菱形的周长.
由于菱形的四条边都相等,
所以要求其周长就要先求
出其边长.由菱形的性质
可知,其对角线互相垂直平分,因此可以在直角
三角形中利用勾股定理来进行计算.
导引:
探索新知
∵四边形ABCD是菱形,
∴AC⊥BD,AO= AC,BO= BD.
∵AC=6 cm,BD=12 cm,
∴AO=3 cm,BO=6 cm.
在Rt△ABO中,由勾股定理,
得AB=
∴菱形的周长=4AB
解:
探索新知
总 结
菱形的对角线将菱形分成四个全等的直角三角形,我们通常将菱形问题中求相关线段的长转化为求直角三角形中相关线段的长,再利用勾股定理来计算.
典题精讲
1 如图,四边形ABCD是菱形,BE⊥AD,BF⊥CD,垂足分别为E,F.
(1)求证:BE=BF;
(2)当菱形ABCD的对角线AC=8,BD=6时,求BE的长.
典题精讲
(1)证明:∵四边形ABCD是菱形,
∴AB=CB,∠BAD=∠BCD.
∵BE⊥AD,BF⊥CD,
∴∠AEB=∠CFB=90°.
典题精讲
(2)解:∵对角线AC=8,BD=8,
∴AO=4,OD=3.易求得AD=5.
又∵菱形ABCD的面积=AD·BE= AC·BD,
∴5BE=
典题精讲
如图,四边形ABCD是菱形,AC=8,DB=6, DH⊥AB于H,则DH等于( )
A. B. C.5 D.4
A
学以致用
小试牛刀
1.有一组________相等的平行四边形叫做菱形?因此有:平行四边形+___________ 菱形.
2 .菱形是轴对称图形?其对称轴的条数为( )
A .2条 B.4条 C.6条 D.8条
邻边
邻边相等
A
3.菱形的________相等.边长为3 cm的菱形周长为________.
4.在菱形ABCD中,∠A=60°,其周长为24 cm,则菱形的面积为________cm2.
四条边
12 cm
18
小试牛刀
5.菱形的对角线__________________,且每条对角线______________.菱形的面积等于两条对角线长的乘积的______;对角线所在的直线是菱形的________.
互相平分且垂直
平分一组对角
一半
对称轴
6.如图,在菱形ABCD中,∠ABC=120°,AB=10 cm,点P是这个菱形内部或边上的一点,若以P,B,C为顶点的三角形是等腰三角形,则P,A(P,A两点不重合)两点间的最短距离为____________cm.
(10 -10)
小试牛刀
7.如图,在△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是( )
A.AB=AC B.AD=BD
C.BE⊥AC D.BE平分∠ABC
D
小试牛刀
8.如图,菱形ABCD的边AB=8,∠B=60°,P是AB上一点,BP=3,Q是CD边上一动点,将梯形APQD沿直线PQ折叠,A的对应点为A′.当CA′的长度最小时,CQ的长为( )
A.5 B.7 C.8 D.
B
小试牛刀
9.如图,菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边的中点,连接EF.若EF= ,BD=2,则菱形ABCD的面积为( )
A.2 B.
C.6 D.8
A
小试牛刀
10.如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE.求证:
(1)∠CEB=∠CBE;
证明:∵△ABC≌△ABD,
∴∠ABC=∠ABD.
∵CE∥BD,∴∠CEB=∠DBE.
∴∠CEB=∠CBE.
小试牛刀
(2)四边形BCED是菱形.
证明:∵△ABC≌△ABD,∴BC=BD.
由(1)得∠CEB=∠CBE,
∴CE=CB.∴CE=BD.
∵CE∥BD,
∴四边形BCED是平行四边形.
又∵BC=BD,∴四边形BCED是菱形.
小试牛刀
11.如图,在菱形ABCD中,过点D作DE⊥AB于点E,作DF⊥BC于点F,连接EF.求证:∠BEF=∠BFE.
证明: ∵四边形ABCD是菱形,
∴AB=CB.
∵△ADE≌△CDF,∴AE=CF.
∴BE=BF.∴∠BEF=∠BFE.
小试牛刀
12.如图,在菱形ABCD中,对角线AC,BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
(1)求证:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长.
∵四边形ABCD是菱形,
∴AB∥CD,AC⊥BD.
∵DE⊥BD,∴DE∥AC.
∴四边形ACDE是平行四边形.
(1)证明:
小试牛刀
∵四边形ABCD是菱形,AC=8,BD=6,
∴AO=4,DO=3,AC⊥BD.
∴AD=CD= =5.
∵四边形ACDE是平行四边形,
∴AE=CD=5,DE=AC=8.
∴△ADE的周长为AD+AE+DE=5+5+8=18.
(2)解:
课堂小结
课堂小结
定义 有一组邻边相等的平行四边形叫做菱形 性质 对称性 菱形是轴对称图形,对称轴是两条对角线所在的直线
边 定理1:菱形的四条边相等
对角线 定理2:菱形的对角线互相垂直,每一条对角线平分一组对角
周长 L=4a
面积 (1)S=ah
(2)菱形的面积等于对角线乘积的一半
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
1.1 菱形的性质与判定
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
下面几幅图片中都含有一些平行四边形.观察这些平行四边形,你能发现它们有什么样的共同特征?
新课精讲
探索新知
1
知识点
菱形的定义
菱形的定义:有一组邻边相等的平行四边形叫做菱形.
要点精析:
(1)菱形必须满足两个条件:一是平行四边形;二是一组邻边相等.二者必须同时具备,缺一不可.
(2)菱形的定义既是菱形的基本性质,也是菱形的基本判定方法.
典题精讲
如图,若要使平行四边形ABCD成为菱形,则需要添加的条件是( )
A.AB=CD
B.AD=BC
C.AB=BC
D.AC=BD
C
典题精讲
2 如图,在△ABC中,AB≠AC,D是BC上一点,DE∥AC交AB于点E,DF∥AB交AC于点F,要使四边形AEDF是菱形,只需添加的条件是( )
A.AD⊥BC
B.∠BAD=∠CAD
C.BD=DC
D.AD=BD
B
探索新知
2
知识点
菱形边的性质
菱形具有平行四边形的所有性质.此外,菱形还具有哪些特殊性质呢 根据菱形的轴对称性,你发现菱形的四条边具有什么大小关系
问 题
菱形的四条边都相等.
探索新知
例1 如图所示,菱形ABCD中,∠B=60°,AB=2,E、F分别是BC、CD的中点,连接AE、EF、AF,则△AEF的周长为( )
A. B.
C. D.3
分析:在菱形ABCD中,因为∠B=60°,连接AC,则△ABC是等边三角形,又因为E分别是BC的中点,所以AE垂直于BC,因此AE= ,所以△AEF的周长为 ,故选B.
B
探索新知
总 结
在菱形中作辅助线经常连接对角线,构造
三角形来做题,能够迎刃而解.
典题精讲
1 边长为3 cm的菱形的周长是( )
A.6 cm B.9 cm
C.12 cm D.15 cm
C
如图,在菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则△AEF的面积是( )
A.4
B.3
C.2
D.
B
探索新知
3
知识点
菱形对角线的性质
因为菱形是平行四边形,所以它具有平行四边形的所有性质.由于它的一组邻边相等,它是否具有一般平行四边形不具有的一些特殊性质呢?
思考
菱形的两条对角线AC与BD之间具有什么位置关系
探索新知
已知:如图,在菱形ABCD中,AB=AD,对角线AC与BD相交于点O.求证(1)AB=BC=CD=AD,(2)AC⊥BD.
证明:
(1)∵四边形ABCD是菱形,
∴AB=CD,AD=BC(菱形的对边相等).
又∵AB=AD,∴AB=BC=CD=AD.
(2)∵AB=AD,∴△ABD是等腰三角形.
又∵四边形ABCD是菱形,∴OB=OD(菱形的对角线互相平分).
在等腰三角形ABD中,∵OB=OD,∴AO⊥BD,
即 AC⊥BD.
探索新知
归 纳
定理 菱形的对角线互相垂直.
探索新知
问 题
菱形的面积如何计算呢?
菱形的面积有两种计算方法:
一种是底乘以高的积;
另一种是对角线乘积的一半.所以在求菱形的面积时,要灵活运用使计算简单.
探索新知
例2 如图,在菱形ABCD中,对角线AC与BD相交于
点O,BD=12 cm,AC=6 cm.求菱形的周长.
由于菱形的四条边都相等,
所以要求其周长就要先求
出其边长.由菱形的性质
可知,其对角线互相垂直平分,因此可以在直角
三角形中利用勾股定理来进行计算.
导引:
探索新知
∵四边形ABCD是菱形,
∴AC⊥BD,AO= AC,BO= BD.
∵AC=6 cm,BD=12 cm,
∴AO=3 cm,BO=6 cm.
在Rt△ABO中,由勾股定理,
得AB=
∴菱形的周长=4AB
解:
探索新知
总 结
菱形的对角线将菱形分成四个全等的直角三角形,我们通常将菱形问题中求相关线段的长转化为求直角三角形中相关线段的长,再利用勾股定理来计算.
典题精讲
1 如图,四边形ABCD是菱形,BE⊥AD,BF⊥CD,垂足分别为E,F.
(1)求证:BE=BF;
(2)当菱形ABCD的对角线AC=8,BD=6时,求BE的长.
典题精讲
(1)证明:∵四边形ABCD是菱形,
∴AB=CB,∠BAD=∠BCD.
∵BE⊥AD,BF⊥CD,
∴∠AEB=∠CFB=90°.
典题精讲
(2)解:∵对角线AC=8,BD=8,
∴AO=4,OD=3.易求得AD=5.
又∵菱形ABCD的面积=AD·BE= AC·BD,
∴5BE=
典题精讲
如图,四边形ABCD是菱形,AC=8,DB=6, DH⊥AB于H,则DH等于( )
A. B. C.5 D.4
A
学以致用
小试牛刀
1.有一组________相等的平行四边形叫做菱形?因此有:平行四边形+___________ 菱形.
2 .菱形是轴对称图形?其对称轴的条数为( )
A .2条 B.4条 C.6条 D.8条
邻边
邻边相等
A
3.菱形的________相等.边长为3 cm的菱形周长为________.
4.在菱形ABCD中,∠A=60°,其周长为24 cm,则菱形的面积为________cm2.
四条边
12 cm
18
小试牛刀
5.菱形的对角线__________________,且每条对角线______________.菱形的面积等于两条对角线长的乘积的______;对角线所在的直线是菱形的________.
互相平分且垂直
平分一组对角
一半
对称轴
6.如图,在菱形ABCD中,∠ABC=120°,AB=10 cm,点P是这个菱形内部或边上的一点,若以P,B,C为顶点的三角形是等腰三角形,则P,A(P,A两点不重合)两点间的最短距离为____________cm.
(10 -10)
小试牛刀
7.如图,在△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是( )
A.AB=AC B.AD=BD
C.BE⊥AC D.BE平分∠ABC
D
小试牛刀
8.如图,菱形ABCD的边AB=8,∠B=60°,P是AB上一点,BP=3,Q是CD边上一动点,将梯形APQD沿直线PQ折叠,A的对应点为A′.当CA′的长度最小时,CQ的长为( )
A.5 B.7 C.8 D.
B
小试牛刀
9.如图,菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边的中点,连接EF.若EF= ,BD=2,则菱形ABCD的面积为( )
A.2 B.
C.6 D.8
A
小试牛刀
10.如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE.求证:
(1)∠CEB=∠CBE;
证明:∵△ABC≌△ABD,
∴∠ABC=∠ABD.
∵CE∥BD,∴∠CEB=∠DBE.
∴∠CEB=∠CBE.
小试牛刀
(2)四边形BCED是菱形.
证明:∵△ABC≌△ABD,∴BC=BD.
由(1)得∠CEB=∠CBE,
∴CE=CB.∴CE=BD.
∵CE∥BD,
∴四边形BCED是平行四边形.
又∵BC=BD,∴四边形BCED是菱形.
小试牛刀
11.如图,在菱形ABCD中,过点D作DE⊥AB于点E,作DF⊥BC于点F,连接EF.求证:∠BEF=∠BFE.
证明: ∵四边形ABCD是菱形,
∴AB=CB.
∵△ADE≌△CDF,∴AE=CF.
∴BE=BF.∴∠BEF=∠BFE.
小试牛刀
12.如图,在菱形ABCD中,对角线AC,BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
(1)求证:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长.
∵四边形ABCD是菱形,
∴AB∥CD,AC⊥BD.
∵DE⊥BD,∴DE∥AC.
∴四边形ACDE是平行四边形.
(1)证明:
小试牛刀
∵四边形ABCD是菱形,AC=8,BD=6,
∴AO=4,DO=3,AC⊥BD.
∴AD=CD= =5.
∵四边形ACDE是平行四边形,
∴AE=CD=5,DE=AC=8.
∴△ADE的周长为AD+AE+DE=5+5+8=18.
(2)解:
课堂小结
课堂小结
定义 有一组邻边相等的平行四边形叫做菱形 性质 对称性 菱形是轴对称图形,对称轴是两条对角线所在的直线
边 定理1:菱形的四条边相等
对角线 定理2:菱形的对角线互相垂直,每一条对角线平分一组对角
周长 L=4a
面积 (1)S=ah
(2)菱形的面积等于对角线乘积的一半
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
