北师大版(新)九上-1.2 矩形的性质与判定 第三课时【优质课件】
文档属性
| 名称 | 北师大版(新)九上-1.2 矩形的性质与判定 第三课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:52:22 | ||
图片预览








文档简介
(共41张PPT)
1.2 矩形的性质与判定
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课前导入
情景导入
1.对角线________的平行四边形是矩形;
对角线________且____________的四边形是矩形.
相等
相等
互相平分
2.有一个角是直角的____________是矩形;
有三个角是________的________是矩形.
平行四边形
直角
四边形
复
习
回
顾
新课精讲
探索新知
1
题型
利用矩形的判定和性质解和差问题
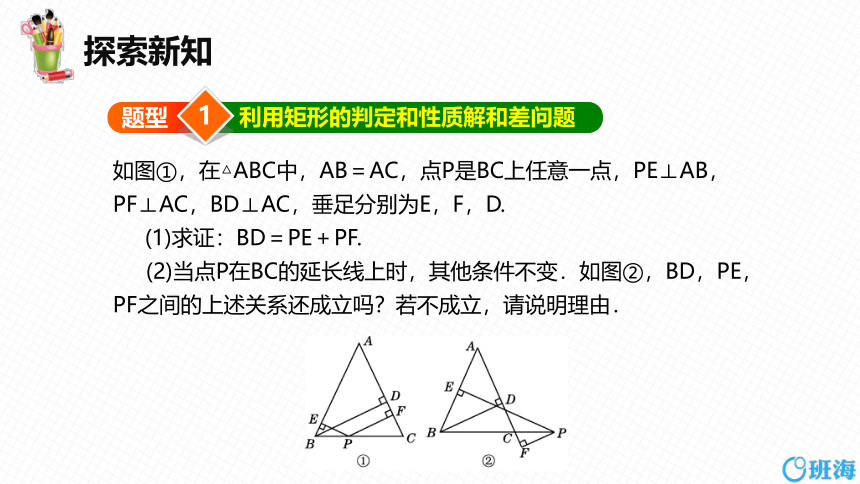
如图①,在△ABC中,AB=AC,点P是BC上任意一点,PE⊥AB,PF⊥AC,BD⊥AC,垂足分别为E,F,D.
(1)求证:BD=PE+PF.
(2)当点P在BC的延长线上时,其他条件不变.如图②,BD,PE,PF之间的上述关系还成立吗?若不成立,请说明理由.
探索新知
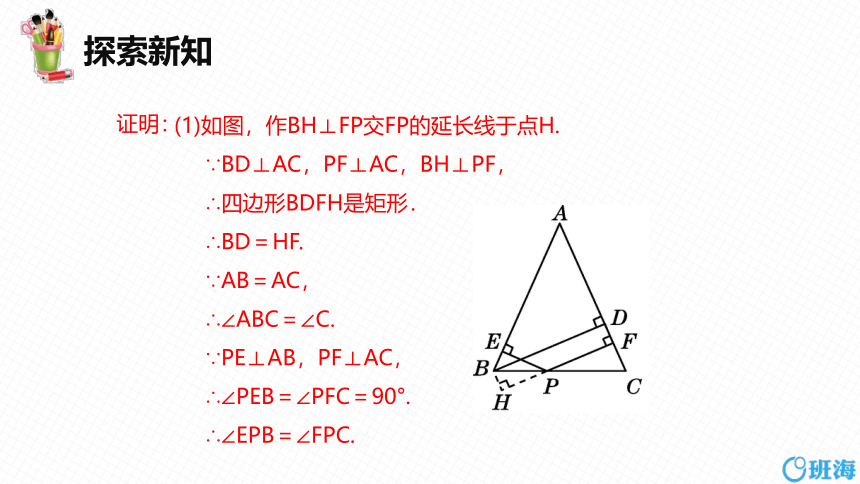
(1)如图,作BH⊥FP交FP的延长线于点H.
∵BD⊥AC,PF⊥AC,BH⊥PF,
∴四边形BDFH是矩形.
∴BD=HF.
∵AB=AC,
∴∠ABC=∠C.
∵PE⊥AB,PF⊥AC,
∴∠PEB=∠PFC=90°.
∴∠EPB=∠FPC.
证明:
探索新知
又∵∠HPB=∠FPC,
∴∠EPB=∠HPB.
∵PE⊥AB,PH⊥BH,
∴∠PEB=∠PHB=90°.
又∵PB=PB,
∴△PEB≌△PHB. 则PE=PH.
∴BD=HF=PF+PH=PF+PE.
即BD=PE+PF.
探索新知
(2)不成立,PE=BD+PF.
理由:作BH⊥PF交PF的延长线于点H.
与(1)同理可得PE=PH,BD=HF.
∴PE=FH+FP=BD+PF.
解:
探索新知
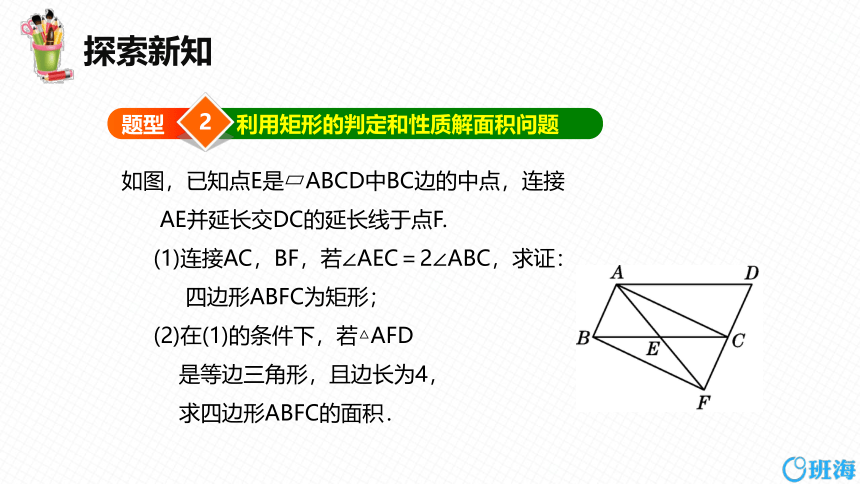
如图,已知点E是 ABCD中BC边的中点,连接
AE并延长交DC的延长线于点F.
(1)连接AC,BF,若∠AEC=2∠ABC,求证:
四边形ABFC为矩形;
(2)在(1)的条件下,若△AFD
是等边三角形,且边长为4,
求四边形ABFC的面积.
2
题型
利用矩形的判定和性质解面积问题
探索新知
(1)∵四边形ABCD为平行四边形,
∴AB∥DC.
∴∠ABE=∠ECF.
又∵点E为BC的中点,
∴BE=CE.
又∵∠AEB=∠FEC,
∴△ABE≌△FCE.
∴AB=CF.
证明:
又AB∥CF,
∴四边形ABFC为平行四边形.
∴AE=EF.
∵∠AEC为△ABE的外角,
∴∠AEC=∠ABC+∠EAB.
又∵∠AEC=2∠ABC,
∴∠ABC=∠EAB.∴AE=BE.
∴AE+EF=BE+CE,即AF=BC.
∴四边形ABFC为矩形.
探索新知
(2)∵四边形ABFC是矩形,
∴AC⊥DF.
又∵△AFD是等边三角形,且边长为4,
∴CF=CD= =2.
∴AC=
∴S矩形ABFC=
解:
探索新知
如图,菱形ABCD的对角线AC,BD相交于点O,且DE∥AC,AE∥BD.
求证:四边形AODE是矩形.
3
题型
利用矩形的定义判定与菱形有关的矩形
∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形.
∵四边形ABCD是菱形,
∴AC⊥BD.
∴∠AOD=90°.
∴四边形AODE是矩形.
证明:
探索新知
如图,已知∠ACB=∠ADB=90°,N,M分别是AB,CD的中点,判断MN与CD的位置关系,并说明理由.
4
题型
利用直角三角形斜边上中线性质判断直线位置关系
探索新知
MN⊥CD. 理由如下:
如图,连接ND,NC.
在Rt△ABD中,∠ADB=90°,N是AB的中点,
∴ND= AB.同理可证NC= AB.
∴ND=NC. ∴△NDC是等腰三角形.
在等腰三角形NDC中,
∵M是CD的中点,
∴MN⊥CD.
解:
探索新知
阅读下面材料:
在数学课上,老师请同学思考如下问题:如图①,我们把一个四边形ABCD 的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?
5
题型
利用矩形、菱形的判定探究条件
探索新知
小敏在思考问题时,有如下思路:连接AC.
点E,F分别是AB,BC的中点
EF∥GH
EF= AC
点G,H分别是CD,AD的中点
GH∥AC
GH= AC
EF∥GH
EF=GH
四边形EFGH
是平行四边形
探索新知
参考小敏思考问题的方法,解决以下问题:
(1)若只改变图①中四边形ABCD的形状(如图②),则四边形EFGH还是平行四边形吗?请说明理由.
(2)如图②,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形?写出结论并说明理由.
②当AC与BD满足什么条件时,四边形EFGH是矩形.直接写出结论.
探索新知
(1)四边形EFGH还是平行四边形.理由如下:
连接AC.
∵E,F分别是AB,BC的中点,
∴EF∥AC,EF= AC.
∵G,H分别是CD,AD的中点,
∴GH∥AC, GH= AC.
∴EF∥GH,EF=GH.
∴四边形EFGH是平行四边形.
解:
探索新知
(2)①当AC=BD时,四边形EFGH是菱形.
理由如下:
由(1)可知四边形EFGH是平行四边形,
当AC=BD时,FG= BD,EF= AC,
∴ FG=EF.
∴四边形EFGH是菱形.
②当AC⊥BD时,四边形EFGH是矩形.
点拨:(2)②中由(1)可知四边形EFGH是平行四边形,
探索新知
∵E,F分别是AB,BC的中点,
∴EF∥AC.
∵AC⊥BD,∴EF⊥BD.
∵G,F分别是CD,BC的中点,
∴FG∥BD.
∵EF⊥BD,
∴EF⊥FG.即∠EFG=90°.
∴四边形EFGH是矩形.
探索新知
已知点E是矩形ABCD的对角线BD上的一点,且BE=BC,AB=3,BC=4,点P是EC上的一动点,且PQ⊥BC于点Q,PR⊥BD于点R.
6
题型
利用矩形的性质探究动点问题
探索新知
(1)如图①,当点P为线段EC的中点时,
求证:PR+PQ=
(2)如图②,当点P为线段EC上任意一点(不与点E,点
C重合)时,其他条件不变,则(1)中的结论是否仍成
立?若成立,请给予证明;若不成立,请说明理由.
(3)如图③,当点P为线段EC延长线上任意一点时,其
他条件不变,则PR与PQ之间又具有怎样的数量关系?
请直接写出你的猜想.
探索新知
(1)连接BP,作CH⊥BD于点H.
∵BE=BC,点P为CE的中点,
∴BP是∠EBC的平分线.
∵PR⊥BE,PQ⊥BC,
∴PR=PQ.
在矩形ABCD中,∠BCD=90°,
BC=4,CD=AB=3,
∴
证明:
探索新知
由S△BCD= BC·CD= BD·CH,
得CH =
∵S△PBE+S△PBC=S△BCE,
∴
又∵BE=BC,
∴PR+PQ=
探索新知
(2)(1)中结论PR+PQ= 仍成立.
证明:连接BP,作CH⊥BD于H.
∵S△PBE+S△PBC=S△BCE,
∴
又∵BE=BC,
∴PR+PQ=CH. 而CH=
∴PR+PQ=
∴(1)中结论成立.
(3)猜想:PR-PQ=
解:
解:
学以致用
小试牛刀
1.如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )
A.4.8 B.5
C.6 D.7.2
A
小试牛刀
2.下列关于矩形的说法中正确的是( )
A.对角线相等的四边形是矩形
B.矩形的对角线相等且互相平分
C.对角线互相平分的四边形是矩形
D.矩形的对角线互相垂直且平分
B
小试牛刀
3.下列说法:
①三角形的三条高一定都在三角形内;
②有一个角是直角的四边形是矩形;
③两边及一角对应相等的两个三角形全等;
④一组对边平行,另一组对边相等的四边形是平行四边形.
其中正确的有( )
A.0个 B.1个 C.2个 D.3个
A
小试牛刀
4.已知 ABCD,AC,BD是它的两条对角线,那么下列条件中,能判断这个平行四边形为矩形的是( )
A.∠BAC=∠DCA B.∠BAC=∠DAC
C.∠BAC=∠ABD D.∠BAC=∠ADB
C
小试牛刀
5.如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH成为矩形,应添加的条件是( )
A.AB∥DC
B.AC=BD
C.AC⊥BD
D.AB=DC
C
小试牛刀
6.如图,分别以△ABC的三边为一边在BC的同侧作三个等边三角形,即△ABD,△BCE,△ACF.请解答下列问题:当△ABC满足什么条件时,四边形ADEF是矩形?
若四边形ADEF为矩形,则∠DAF=90°.
∵∠DAB=∠FAC=60°,
∴∠BAC=360°-∠DAB-∠FAC-∠DAF=
360°-60°-60°-90°=150°.
∴当△ABC满足∠BAC=150°时,
四边形ADEF是矩形.
小试牛刀
(2)当△ABC满足什么条件时,四边形ADEF是矩形?
若四边形ADEF为矩形,则∠DAF=90°.
∵∠DAB=∠FAC=60°,
∴∠BAC=360°-∠DAB-∠FAC-∠DAF=
360°-60°-60°-90°=150°.
∴当△ABC满足∠BAC=150°时,
四边形ADEF是矩形.
小试牛刀
7.如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处.
(1)求证:四边形AECF是
平行四边形;
小试牛刀
由题意可得AM=AB,CN=CD,∠FNC=∠D=90°,∠AME=∠B=90°.∴∠ANF=90°,∠CME=90°.
∴∠ANF=∠CME.
∵四边形ABCD为矩形,∴AB=CD,AD∥BC.
∴AM=CN,∠FAN=∠ECM.
∴AM-MN=CN-MN,即AN=CM.
证明:
小试牛刀
在△ANF和△CME中,
∠FAN=∠ECM,
AN=CM,
∠ANF=∠CME,
∴△ANF≌△CME(ASA).
∴AF=CE.
又∵AF∥CE,∴四边形AECF是平行四边形.
小试牛刀
8.如图,在△ABC中,∠A=90°,D是AC上的一 点,BD=DC,P是BC上的任意一点,PE⊥BD,PF⊥AC,E,F为垂足.试判断线段PE,PF,AB之间的数量关系,并说明理由.
小试牛刀
PE+PF=AB.
理由:过点P作PG⊥AB于G,交BD于O,如图所示.
∵PF⊥AC,∠A=90°,
∴∠A=∠AGP=∠PFA=90°.
∴四边形AGPF是矩形.
∴AG=PF,PG∥AC.
解:
小试牛刀
又∵BD=DC,∴∠C=∠GPB=∠DBP. ∴OB=OP.
∵PG⊥AB,PE⊥BD,∴∠BGO=∠PEO=90°.
在△BGO和△PEO中,
∠BGO=∠PEO,
∠GOB=∠EOP,
OB=OP,
∴△BGO≌△PEO.∴BG=PE.
∵AB=BG+AG,∴PE+PF=AB.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
1.2 矩形的性质与判定
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课前导入
情景导入
1.对角线________的平行四边形是矩形;
对角线________且____________的四边形是矩形.
相等
相等
互相平分
2.有一个角是直角的____________是矩形;
有三个角是________的________是矩形.
平行四边形
直角
四边形
复
习
回
顾
新课精讲
探索新知
1
题型
利用矩形的判定和性质解和差问题
如图①,在△ABC中,AB=AC,点P是BC上任意一点,PE⊥AB,PF⊥AC,BD⊥AC,垂足分别为E,F,D.
(1)求证:BD=PE+PF.
(2)当点P在BC的延长线上时,其他条件不变.如图②,BD,PE,PF之间的上述关系还成立吗?若不成立,请说明理由.
探索新知
(1)如图,作BH⊥FP交FP的延长线于点H.
∵BD⊥AC,PF⊥AC,BH⊥PF,
∴四边形BDFH是矩形.
∴BD=HF.
∵AB=AC,
∴∠ABC=∠C.
∵PE⊥AB,PF⊥AC,
∴∠PEB=∠PFC=90°.
∴∠EPB=∠FPC.
证明:
探索新知
又∵∠HPB=∠FPC,
∴∠EPB=∠HPB.
∵PE⊥AB,PH⊥BH,
∴∠PEB=∠PHB=90°.
又∵PB=PB,
∴△PEB≌△PHB. 则PE=PH.
∴BD=HF=PF+PH=PF+PE.
即BD=PE+PF.
探索新知
(2)不成立,PE=BD+PF.
理由:作BH⊥PF交PF的延长线于点H.
与(1)同理可得PE=PH,BD=HF.
∴PE=FH+FP=BD+PF.
解:
探索新知
如图,已知点E是 ABCD中BC边的中点,连接
AE并延长交DC的延长线于点F.
(1)连接AC,BF,若∠AEC=2∠ABC,求证:
四边形ABFC为矩形;
(2)在(1)的条件下,若△AFD
是等边三角形,且边长为4,
求四边形ABFC的面积.
2
题型
利用矩形的判定和性质解面积问题
探索新知
(1)∵四边形ABCD为平行四边形,
∴AB∥DC.
∴∠ABE=∠ECF.
又∵点E为BC的中点,
∴BE=CE.
又∵∠AEB=∠FEC,
∴△ABE≌△FCE.
∴AB=CF.
证明:
又AB∥CF,
∴四边形ABFC为平行四边形.
∴AE=EF.
∵∠AEC为△ABE的外角,
∴∠AEC=∠ABC+∠EAB.
又∵∠AEC=2∠ABC,
∴∠ABC=∠EAB.∴AE=BE.
∴AE+EF=BE+CE,即AF=BC.
∴四边形ABFC为矩形.
探索新知
(2)∵四边形ABFC是矩形,
∴AC⊥DF.
又∵△AFD是等边三角形,且边长为4,
∴CF=CD= =2.
∴AC=
∴S矩形ABFC=
解:
探索新知
如图,菱形ABCD的对角线AC,BD相交于点O,且DE∥AC,AE∥BD.
求证:四边形AODE是矩形.
3
题型
利用矩形的定义判定与菱形有关的矩形
∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形.
∵四边形ABCD是菱形,
∴AC⊥BD.
∴∠AOD=90°.
∴四边形AODE是矩形.
证明:
探索新知
如图,已知∠ACB=∠ADB=90°,N,M分别是AB,CD的中点,判断MN与CD的位置关系,并说明理由.
4
题型
利用直角三角形斜边上中线性质判断直线位置关系
探索新知
MN⊥CD. 理由如下:
如图,连接ND,NC.
在Rt△ABD中,∠ADB=90°,N是AB的中点,
∴ND= AB.同理可证NC= AB.
∴ND=NC. ∴△NDC是等腰三角形.
在等腰三角形NDC中,
∵M是CD的中点,
∴MN⊥CD.
解:
探索新知
阅读下面材料:
在数学课上,老师请同学思考如下问题:如图①,我们把一个四边形ABCD 的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?
5
题型
利用矩形、菱形的判定探究条件
探索新知
小敏在思考问题时,有如下思路:连接AC.
点E,F分别是AB,BC的中点
EF∥GH
EF= AC
点G,H分别是CD,AD的中点
GH∥AC
GH= AC
EF∥GH
EF=GH
四边形EFGH
是平行四边形
探索新知
参考小敏思考问题的方法,解决以下问题:
(1)若只改变图①中四边形ABCD的形状(如图②),则四边形EFGH还是平行四边形吗?请说明理由.
(2)如图②,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形?写出结论并说明理由.
②当AC与BD满足什么条件时,四边形EFGH是矩形.直接写出结论.
探索新知
(1)四边形EFGH还是平行四边形.理由如下:
连接AC.
∵E,F分别是AB,BC的中点,
∴EF∥AC,EF= AC.
∵G,H分别是CD,AD的中点,
∴GH∥AC, GH= AC.
∴EF∥GH,EF=GH.
∴四边形EFGH是平行四边形.
解:
探索新知
(2)①当AC=BD时,四边形EFGH是菱形.
理由如下:
由(1)可知四边形EFGH是平行四边形,
当AC=BD时,FG= BD,EF= AC,
∴ FG=EF.
∴四边形EFGH是菱形.
②当AC⊥BD时,四边形EFGH是矩形.
点拨:(2)②中由(1)可知四边形EFGH是平行四边形,
探索新知
∵E,F分别是AB,BC的中点,
∴EF∥AC.
∵AC⊥BD,∴EF⊥BD.
∵G,F分别是CD,BC的中点,
∴FG∥BD.
∵EF⊥BD,
∴EF⊥FG.即∠EFG=90°.
∴四边形EFGH是矩形.
探索新知
已知点E是矩形ABCD的对角线BD上的一点,且BE=BC,AB=3,BC=4,点P是EC上的一动点,且PQ⊥BC于点Q,PR⊥BD于点R.
6
题型
利用矩形的性质探究动点问题
探索新知
(1)如图①,当点P为线段EC的中点时,
求证:PR+PQ=
(2)如图②,当点P为线段EC上任意一点(不与点E,点
C重合)时,其他条件不变,则(1)中的结论是否仍成
立?若成立,请给予证明;若不成立,请说明理由.
(3)如图③,当点P为线段EC延长线上任意一点时,其
他条件不变,则PR与PQ之间又具有怎样的数量关系?
请直接写出你的猜想.
探索新知
(1)连接BP,作CH⊥BD于点H.
∵BE=BC,点P为CE的中点,
∴BP是∠EBC的平分线.
∵PR⊥BE,PQ⊥BC,
∴PR=PQ.
在矩形ABCD中,∠BCD=90°,
BC=4,CD=AB=3,
∴
证明:
探索新知
由S△BCD= BC·CD= BD·CH,
得CH =
∵S△PBE+S△PBC=S△BCE,
∴
又∵BE=BC,
∴PR+PQ=
探索新知
(2)(1)中结论PR+PQ= 仍成立.
证明:连接BP,作CH⊥BD于H.
∵S△PBE+S△PBC=S△BCE,
∴
又∵BE=BC,
∴PR+PQ=CH. 而CH=
∴PR+PQ=
∴(1)中结论成立.
(3)猜想:PR-PQ=
解:
解:
学以致用
小试牛刀
1.如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )
A.4.8 B.5
C.6 D.7.2
A
小试牛刀
2.下列关于矩形的说法中正确的是( )
A.对角线相等的四边形是矩形
B.矩形的对角线相等且互相平分
C.对角线互相平分的四边形是矩形
D.矩形的对角线互相垂直且平分
B
小试牛刀
3.下列说法:
①三角形的三条高一定都在三角形内;
②有一个角是直角的四边形是矩形;
③两边及一角对应相等的两个三角形全等;
④一组对边平行,另一组对边相等的四边形是平行四边形.
其中正确的有( )
A.0个 B.1个 C.2个 D.3个
A
小试牛刀
4.已知 ABCD,AC,BD是它的两条对角线,那么下列条件中,能判断这个平行四边形为矩形的是( )
A.∠BAC=∠DCA B.∠BAC=∠DAC
C.∠BAC=∠ABD D.∠BAC=∠ADB
C
小试牛刀
5.如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH成为矩形,应添加的条件是( )
A.AB∥DC
B.AC=BD
C.AC⊥BD
D.AB=DC
C
小试牛刀
6.如图,分别以△ABC的三边为一边在BC的同侧作三个等边三角形,即△ABD,△BCE,△ACF.请解答下列问题:当△ABC满足什么条件时,四边形ADEF是矩形?
若四边形ADEF为矩形,则∠DAF=90°.
∵∠DAB=∠FAC=60°,
∴∠BAC=360°-∠DAB-∠FAC-∠DAF=
360°-60°-60°-90°=150°.
∴当△ABC满足∠BAC=150°时,
四边形ADEF是矩形.
小试牛刀
(2)当△ABC满足什么条件时,四边形ADEF是矩形?
若四边形ADEF为矩形,则∠DAF=90°.
∵∠DAB=∠FAC=60°,
∴∠BAC=360°-∠DAB-∠FAC-∠DAF=
360°-60°-60°-90°=150°.
∴当△ABC满足∠BAC=150°时,
四边形ADEF是矩形.
小试牛刀
7.如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处.
(1)求证:四边形AECF是
平行四边形;
小试牛刀
由题意可得AM=AB,CN=CD,∠FNC=∠D=90°,∠AME=∠B=90°.∴∠ANF=90°,∠CME=90°.
∴∠ANF=∠CME.
∵四边形ABCD为矩形,∴AB=CD,AD∥BC.
∴AM=CN,∠FAN=∠ECM.
∴AM-MN=CN-MN,即AN=CM.
证明:
小试牛刀
在△ANF和△CME中,
∠FAN=∠ECM,
AN=CM,
∠ANF=∠CME,
∴△ANF≌△CME(ASA).
∴AF=CE.
又∵AF∥CE,∴四边形AECF是平行四边形.
小试牛刀
8.如图,在△ABC中,∠A=90°,D是AC上的一 点,BD=DC,P是BC上的任意一点,PE⊥BD,PF⊥AC,E,F为垂足.试判断线段PE,PF,AB之间的数量关系,并说明理由.
小试牛刀
PE+PF=AB.
理由:过点P作PG⊥AB于G,交BD于O,如图所示.
∵PF⊥AC,∠A=90°,
∴∠A=∠AGP=∠PFA=90°.
∴四边形AGPF是矩形.
∴AG=PF,PG∥AC.
解:
小试牛刀
又∵BD=DC,∴∠C=∠GPB=∠DBP. ∴OB=OP.
∵PG⊥AB,PE⊥BD,∴∠BGO=∠PEO=90°.
在△BGO和△PEO中,
∠BGO=∠PEO,
∠GOB=∠EOP,
OB=OP,
∴△BGO≌△PEO.∴BG=PE.
∵AB=BG+AG,∴PE+PF=AB.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
