北师大版(新)九上-1.2 矩形的性质与判定 第一课时【优质课件】
文档属性
| 名称 | 北师大版(新)九上-1.2 矩形的性质与判定 第一课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:52:22 | ||
图片预览










文档简介
(共36张PPT)
1.2 矩形的性质与判定
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
下面图片中都含有一些特殊的平行四边形.观察这些特殊的平行四边形,你能发现它们有什么样的共同特征?
新课精讲
探索新知
1
知识点
矩形的定义
矩形的定义:有一个角是直角的平行四边形叫做矩形.
注意:
(1)由矩形的定义知,矩形一定是平行四边形,但平行四边形不一定是矩形.
(2)矩形必须具备两个条件:①它是一个平行四边形;②它有一个角是直角.这两个条件缺一不可.
探索新知
例1 如图所示,l1∥l2,A、B是l1上的两点,过A、B分别作l2的垂线,垂足分别为D、C.四边形ABCD是矩形吗 简述你的理由.
分析:很容易发现ABCD为平行四边形只需有一个角为直角即可,因为AD⊥l2有直角,问题得证.
解:四边形ABCD是矩形,理由:∵AD⊥l2,BC⊥l2,
∴AD∥BC.∵l1∥l2,
∴四边形ABCD是平行四边形.
又∵∠ADC=90°,∴平行四边形ABCD为矩形.
探索新知
总 结
利用定义识别一个四边形是矩形,首先要证明
四边形是平行四边形,然后证明平行四边形有一个
角是直角.
典题精讲
下列说法正确的是( )
A.平行四边形是矩形
B.矩形不一定是平行四边形
C.有一个角是直角的四边形是矩形
D.平行四边形具有的性质矩形都具有
B
探索新知
2
知识点
矩形的边角性质
想一想
(1)矩形是特殊的平行四边形,它具有一般平行四边形的所有性
质.你能列举一些这样的性质吗?
(2)矩形是轴对称图形吗?
如果是,它有几条对称轴?
(3)你认为矩形还具有哪些
特殊的性质?与同伴交流.
矩形是轴
对称图形.
探索新知
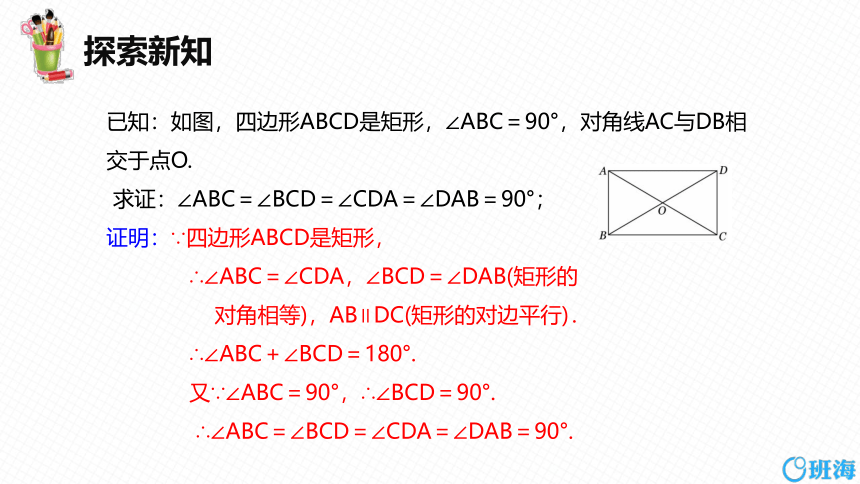
已知:如图,四边形ABCD是矩形,∠ABC=90°,对角线AC与DB相交于点O.
求证:∠ABC=∠BCD=∠CDA=∠DAB=90°;
证明:∵四边形ABCD是矩形,
∴∠ABC=∠CDA,∠BCD=∠DAB(矩形的
对角相等),AB∥DC(矩形的对边平行).
∴∠ABC+∠BCD=180°.
又∵∠ABC=90°,∴∠BCD=90°.
∴∠ABC=∠BCD=∠CDA=∠DAB=90°.
探索新知
归 纳
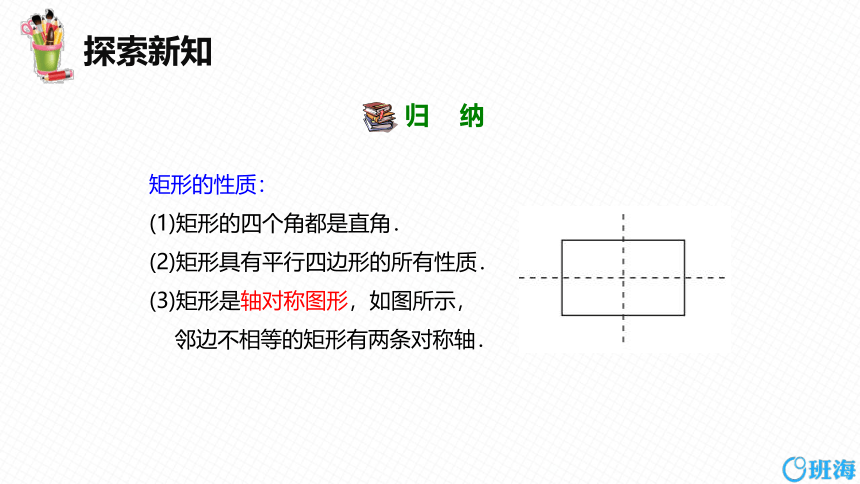
矩形的性质:
(1)矩形的四个角都是直角.
(2)矩形具有平行四边形的所有性质.
(3)矩形是轴对称图形,如图所示,
邻边不相等的矩形有两条对称轴.
典题精讲
如图,点E是矩形ABCD的边AD延长线上的一点,且AD=DE,连接BE交CD于点O,连接AO,下列结论中不正确的是( )
A.△AOB≌△BOC
B.△BOC≌△EOD
C.△AOD≌△EOD
D.△AOD≌△BOC
A
探索新知
3
知识点
矩形的对角线性质
任意画一个矩形,作出它的两条对角线,并比较它们的长.你有什么发现
已知:如图所示,四边形ABCD是矩形.
求证:AC=DB.
证明:∵四边形ABCD是矩形,
∴∠ABC=∠DCB=90°(矩形的性质定理1).
∵AB=CD(平行四边形的对边相等),BC=CB.
∴△ABC≌△DCB(SAS). ∴AC=DB.
于是,就得到矩形的性质:矩形的对角线相等.
典题精讲
矩形具有而一般平行四边形不具有的性质是( )
A.对角相等
B.对角线相等
C.对边相等
D.对角线互相平分
B
探索新知
4
知识点
直角三角形斜边上中线的性质
议一议
如图,矩形ABCD的对角线AC与BD交于点E,那么BE是Rt△ABC中一条怎样的特殊线段?它与AC有什么大小关系?由此你能得到怎样的结论?
探索新知
1、结论:定理:直角三角形斜边上的中线等于斜边的一半.
2、请你完成这个定理的证明.
3、总结:(1)此性质与“含30°角的直角三角形性质”及“三角形中位线性质”是解决线段倍分问题的重要依据;
(2)“三角形中位线性质”适用于任何三角形;“直角三角形斜边上的中线性质”适用于任何直角三角形;“含30°角的直角三角形性质”仅适用于含30°角的特殊直角三角形;
(3)直角三角形还具有以下性质:①两锐角互余;②两直角边的平方和等于斜边平方.
探索新知
例2 如图,在矩形ABCD中,两条对角线相交于点O,
∠AOD=120°,AB=2.5,求这个矩形对角线的长.
解:∵四边形ABCD是矩形,
∴AC=BD(矩形的对角线相等),
OA=OC= AC,OB=OD= BD(矩形的对角线互相平分).
∴OA=OD.
∵∠AOD=120°,
∴∠ODA=∠OAD= (180°-120°)=30°.
又∵∠DAB=90°(矩形的四个角都是直角),
∴BD=2AB=2×2.5=5.
你还有其他解法吗?
典题精讲
1
如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( )
A.14
B.16
C.17
D.18
D
典题精讲
2
如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=4,则BF的长为( )
A.4
B.8
C.2
D.4
D
学以致用
小试牛刀
1.有一个角是_______的平行四边形是矩形,它包含两层含义:一是____________+一直角可得矩形;二是矩形一定是____________且有一个角是_____.
直角
平行四边形
平行四边形
直角
2.矩形的四个角都是_________;矩形的对边________且________.
直角
平行
相等
3.矩形的对角线________且____________,它的两条对角线把矩形分成________个等腰三角形.
相等
互相平分
4
小试牛刀
4.根据矩形的两条对角线相等且互相平分,将矩形沿一条对角线切去一半后,可得出直角三角形斜边上的中线__________________.
等于斜边的一半
5.如图,矩形ABCD的对角线AC与BD相交于点O,∠ADB=30°,AB=4,则OC等于 ( )
A.5 B.4
C.3.5 D.3
B
小试牛刀
6.如图,四边形ABCD的对角线互相平分,要使它成为矩形,需要添加的条件是( )
A.AB=CD
B.AD=BC
C.∠AOB=45°
D.∠ABC=90°
D
小试牛刀
7.如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )
A.△AFD≌△DCE
B.AF= AD
C.AB=AF
D.BE=AD-DF
B
小试牛刀
8.在探索“尺规三等分角”这个数学名题的过程中,曾利用了如图.该图中,四边形ABCD是矩形,E是BA延长线上一点,
F是CE上一点,∠ACF=∠AFC,
∠FAE=∠FEA.若∠ACB=21°,
则∠ECD的度数是( )
A.7° B.21° C.23° D.24°
C
小试牛刀
9.如图,△ABD是以BD为斜边的等腰直角三角形,在△BCD中,∠DBC=90°,
∠BCD=60°,DC的中点为E,
AD与BE的延长线交于点F,
则∠AFB的度数为( )
A.30° B.15°
C.45° D.25°
B
小试牛刀
10.如图,在矩形ABCD中,E,F分别是 AD,BC的中点,CE,AF分别交BD于G,H两点.(1)求证:四边形AFCE是平行四边形;
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC.
∵E,F分别是AD,BC的中点,
∴AE= AD,CF= BC.
∴AE=CF.
∴四边形AFCE是平行四边形.
证明:
小试牛刀
(2)求证:EG=FH.
证明:∵四边形AFCE是平行四边形,∴CE∥AF.
∴∠DGE=∠AHD=∠BHF.
∵AD∥BC,∴∠EDG=∠FBH.
∵DE= AD,BF= BC,AD=BC,∴DE=BF.
在△DEG和△BFH中,
∠DGE=∠BHF,
∠EDG=∠FBH,
DE=BF,
∴△DEG≌△BFH(AAS). ∴EG=FH.
小试牛刀
11.如图,在矩形ABCD中,∠ABD,∠CDB的平分线BE,DF分别交边AD,BC于点E,F.
求证:四边形BEDF是平行四边形.
∵四边形ABCD是矩形,
∴AB∥DC,AD∥BC. ∴∠ABD=∠CDB.
∵BE平分∠ABD、DF平分∠BDC,
∴∠EBD= ∠ABD, ∠FDB= ∠BDC.
∴∠EBD=∠FDB.∴BE∥DF. 又∵AD∥BC,
∴四边形BEDF是平行四边形.
证明:
小试牛刀
当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.
解:当∠ABE=30°时,四边形BEDF是菱形.
理由:∵BE平分∠ABD,
∴∠ABD=2∠ABE=60°,∠EBD=∠ABE=30°.
∵四边形ABCD是矩形, ∴∠A=90°.
∴∠EDB=90°-∠ABD=30°.
∴∠EDB=∠EBD=30°. ∴EB=ED.
又∵四边形BEDF是平行四边形,
∴四边形BEDF是菱形.
小试牛刀
12.如图,在矩形ABCD中,连接对角线AC,BD,将△ABC沿BC方向平移,使点B移到点C,得到△DCE.
(1)求证:△ACD≌△EDC;
证明:∵四边形ABCD是矩形,
∴AC=BD,AD=BC,∠ADC=∠ABC=90°.
由平移的性质得DE=AC,CE=BC,∠DCE=∠ABC=90°, ∴AD=EC,∠ADC=∠ECD.
在△ACD和△EDC中,
AD=EC,
∠ADC=∠ECD,
CD=DC,
∴△ACD≌△EDC(SAS).
小试牛刀
(2)请探究△BDE的形状,并说明理由.
△BDE是等腰三角形.
理由如下:
∵AC=BD,DE=AC,∴BD=DE.
∴△BDE是等腰三角形.
解:
课堂小结
课堂小结
1.矩形定义:有一个角是直角的平行四边形叫做矩形,因此,矩形是平行四边形的特例,具有平行四边形所有性质.
2.性质归纳:
(1)边的性质:对边平行且相等.
(2)对角线性质:对角线互相平分且相等.
(3)对称性:矩形是轴对称图形.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
1.2 矩形的性质与判定
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
下面图片中都含有一些特殊的平行四边形.观察这些特殊的平行四边形,你能发现它们有什么样的共同特征?
新课精讲
探索新知
1
知识点
矩形的定义
矩形的定义:有一个角是直角的平行四边形叫做矩形.
注意:
(1)由矩形的定义知,矩形一定是平行四边形,但平行四边形不一定是矩形.
(2)矩形必须具备两个条件:①它是一个平行四边形;②它有一个角是直角.这两个条件缺一不可.
探索新知
例1 如图所示,l1∥l2,A、B是l1上的两点,过A、B分别作l2的垂线,垂足分别为D、C.四边形ABCD是矩形吗 简述你的理由.
分析:很容易发现ABCD为平行四边形只需有一个角为直角即可,因为AD⊥l2有直角,问题得证.
解:四边形ABCD是矩形,理由:∵AD⊥l2,BC⊥l2,
∴AD∥BC.∵l1∥l2,
∴四边形ABCD是平行四边形.
又∵∠ADC=90°,∴平行四边形ABCD为矩形.
探索新知
总 结
利用定义识别一个四边形是矩形,首先要证明
四边形是平行四边形,然后证明平行四边形有一个
角是直角.
典题精讲
下列说法正确的是( )
A.平行四边形是矩形
B.矩形不一定是平行四边形
C.有一个角是直角的四边形是矩形
D.平行四边形具有的性质矩形都具有
B
探索新知
2
知识点
矩形的边角性质
想一想
(1)矩形是特殊的平行四边形,它具有一般平行四边形的所有性
质.你能列举一些这样的性质吗?
(2)矩形是轴对称图形吗?
如果是,它有几条对称轴?
(3)你认为矩形还具有哪些
特殊的性质?与同伴交流.
矩形是轴
对称图形.
探索新知
已知:如图,四边形ABCD是矩形,∠ABC=90°,对角线AC与DB相交于点O.
求证:∠ABC=∠BCD=∠CDA=∠DAB=90°;
证明:∵四边形ABCD是矩形,
∴∠ABC=∠CDA,∠BCD=∠DAB(矩形的
对角相等),AB∥DC(矩形的对边平行).
∴∠ABC+∠BCD=180°.
又∵∠ABC=90°,∴∠BCD=90°.
∴∠ABC=∠BCD=∠CDA=∠DAB=90°.
探索新知
归 纳
矩形的性质:
(1)矩形的四个角都是直角.
(2)矩形具有平行四边形的所有性质.
(3)矩形是轴对称图形,如图所示,
邻边不相等的矩形有两条对称轴.
典题精讲
如图,点E是矩形ABCD的边AD延长线上的一点,且AD=DE,连接BE交CD于点O,连接AO,下列结论中不正确的是( )
A.△AOB≌△BOC
B.△BOC≌△EOD
C.△AOD≌△EOD
D.△AOD≌△BOC
A
探索新知
3
知识点
矩形的对角线性质
任意画一个矩形,作出它的两条对角线,并比较它们的长.你有什么发现
已知:如图所示,四边形ABCD是矩形.
求证:AC=DB.
证明:∵四边形ABCD是矩形,
∴∠ABC=∠DCB=90°(矩形的性质定理1).
∵AB=CD(平行四边形的对边相等),BC=CB.
∴△ABC≌△DCB(SAS). ∴AC=DB.
于是,就得到矩形的性质:矩形的对角线相等.
典题精讲
矩形具有而一般平行四边形不具有的性质是( )
A.对角相等
B.对角线相等
C.对边相等
D.对角线互相平分
B
探索新知
4
知识点
直角三角形斜边上中线的性质
议一议
如图,矩形ABCD的对角线AC与BD交于点E,那么BE是Rt△ABC中一条怎样的特殊线段?它与AC有什么大小关系?由此你能得到怎样的结论?
探索新知
1、结论:定理:直角三角形斜边上的中线等于斜边的一半.
2、请你完成这个定理的证明.
3、总结:(1)此性质与“含30°角的直角三角形性质”及“三角形中位线性质”是解决线段倍分问题的重要依据;
(2)“三角形中位线性质”适用于任何三角形;“直角三角形斜边上的中线性质”适用于任何直角三角形;“含30°角的直角三角形性质”仅适用于含30°角的特殊直角三角形;
(3)直角三角形还具有以下性质:①两锐角互余;②两直角边的平方和等于斜边平方.
探索新知
例2 如图,在矩形ABCD中,两条对角线相交于点O,
∠AOD=120°,AB=2.5,求这个矩形对角线的长.
解:∵四边形ABCD是矩形,
∴AC=BD(矩形的对角线相等),
OA=OC= AC,OB=OD= BD(矩形的对角线互相平分).
∴OA=OD.
∵∠AOD=120°,
∴∠ODA=∠OAD= (180°-120°)=30°.
又∵∠DAB=90°(矩形的四个角都是直角),
∴BD=2AB=2×2.5=5.
你还有其他解法吗?
典题精讲
1
如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( )
A.14
B.16
C.17
D.18
D
典题精讲
2
如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=4,则BF的长为( )
A.4
B.8
C.2
D.4
D
学以致用
小试牛刀
1.有一个角是_______的平行四边形是矩形,它包含两层含义:一是____________+一直角可得矩形;二是矩形一定是____________且有一个角是_____.
直角
平行四边形
平行四边形
直角
2.矩形的四个角都是_________;矩形的对边________且________.
直角
平行
相等
3.矩形的对角线________且____________,它的两条对角线把矩形分成________个等腰三角形.
相等
互相平分
4
小试牛刀
4.根据矩形的两条对角线相等且互相平分,将矩形沿一条对角线切去一半后,可得出直角三角形斜边上的中线__________________.
等于斜边的一半
5.如图,矩形ABCD的对角线AC与BD相交于点O,∠ADB=30°,AB=4,则OC等于 ( )
A.5 B.4
C.3.5 D.3
B
小试牛刀
6.如图,四边形ABCD的对角线互相平分,要使它成为矩形,需要添加的条件是( )
A.AB=CD
B.AD=BC
C.∠AOB=45°
D.∠ABC=90°
D
小试牛刀
7.如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )
A.△AFD≌△DCE
B.AF= AD
C.AB=AF
D.BE=AD-DF
B
小试牛刀
8.在探索“尺规三等分角”这个数学名题的过程中,曾利用了如图.该图中,四边形ABCD是矩形,E是BA延长线上一点,
F是CE上一点,∠ACF=∠AFC,
∠FAE=∠FEA.若∠ACB=21°,
则∠ECD的度数是( )
A.7° B.21° C.23° D.24°
C
小试牛刀
9.如图,△ABD是以BD为斜边的等腰直角三角形,在△BCD中,∠DBC=90°,
∠BCD=60°,DC的中点为E,
AD与BE的延长线交于点F,
则∠AFB的度数为( )
A.30° B.15°
C.45° D.25°
B
小试牛刀
10.如图,在矩形ABCD中,E,F分别是 AD,BC的中点,CE,AF分别交BD于G,H两点.(1)求证:四边形AFCE是平行四边形;
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC.
∵E,F分别是AD,BC的中点,
∴AE= AD,CF= BC.
∴AE=CF.
∴四边形AFCE是平行四边形.
证明:
小试牛刀
(2)求证:EG=FH.
证明:∵四边形AFCE是平行四边形,∴CE∥AF.
∴∠DGE=∠AHD=∠BHF.
∵AD∥BC,∴∠EDG=∠FBH.
∵DE= AD,BF= BC,AD=BC,∴DE=BF.
在△DEG和△BFH中,
∠DGE=∠BHF,
∠EDG=∠FBH,
DE=BF,
∴△DEG≌△BFH(AAS). ∴EG=FH.
小试牛刀
11.如图,在矩形ABCD中,∠ABD,∠CDB的平分线BE,DF分别交边AD,BC于点E,F.
求证:四边形BEDF是平行四边形.
∵四边形ABCD是矩形,
∴AB∥DC,AD∥BC. ∴∠ABD=∠CDB.
∵BE平分∠ABD、DF平分∠BDC,
∴∠EBD= ∠ABD, ∠FDB= ∠BDC.
∴∠EBD=∠FDB.∴BE∥DF. 又∵AD∥BC,
∴四边形BEDF是平行四边形.
证明:
小试牛刀
当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.
解:当∠ABE=30°时,四边形BEDF是菱形.
理由:∵BE平分∠ABD,
∴∠ABD=2∠ABE=60°,∠EBD=∠ABE=30°.
∵四边形ABCD是矩形, ∴∠A=90°.
∴∠EDB=90°-∠ABD=30°.
∴∠EDB=∠EBD=30°. ∴EB=ED.
又∵四边形BEDF是平行四边形,
∴四边形BEDF是菱形.
小试牛刀
12.如图,在矩形ABCD中,连接对角线AC,BD,将△ABC沿BC方向平移,使点B移到点C,得到△DCE.
(1)求证:△ACD≌△EDC;
证明:∵四边形ABCD是矩形,
∴AC=BD,AD=BC,∠ADC=∠ABC=90°.
由平移的性质得DE=AC,CE=BC,∠DCE=∠ABC=90°, ∴AD=EC,∠ADC=∠ECD.
在△ACD和△EDC中,
AD=EC,
∠ADC=∠ECD,
CD=DC,
∴△ACD≌△EDC(SAS).
小试牛刀
(2)请探究△BDE的形状,并说明理由.
△BDE是等腰三角形.
理由如下:
∵AC=BD,DE=AC,∴BD=DE.
∴△BDE是等腰三角形.
解:
课堂小结
课堂小结
1.矩形定义:有一个角是直角的平行四边形叫做矩形,因此,矩形是平行四边形的特例,具有平行四边形所有性质.
2.性质归纳:
(1)边的性质:对边平行且相等.
(2)对角线性质:对角线互相平分且相等.
(3)对称性:矩形是轴对称图形.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
