北师大版(新)九上-1.3 正方形的性质与判定 第二课时【优质课件】
文档属性
| 名称 | 北师大版(新)九上-1.3 正方形的性质与判定 第二课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:52:22 | ||
图片预览







文档简介
(共27张PPT)
1.3 正方形的性质与判定
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图,将一张长方形纸对折两次,然后剪下一个角,打开.怎样剪才能剪出一个正方形?
新课精讲
探索新知
1
知识点
正方形的对称性
正方形:既是中心对称图形,又是轴对称图形.它的中心是对称中心,有4条对称轴,分别是两条对角线和每组对边中点连线所在直线.
探索新知
知识点
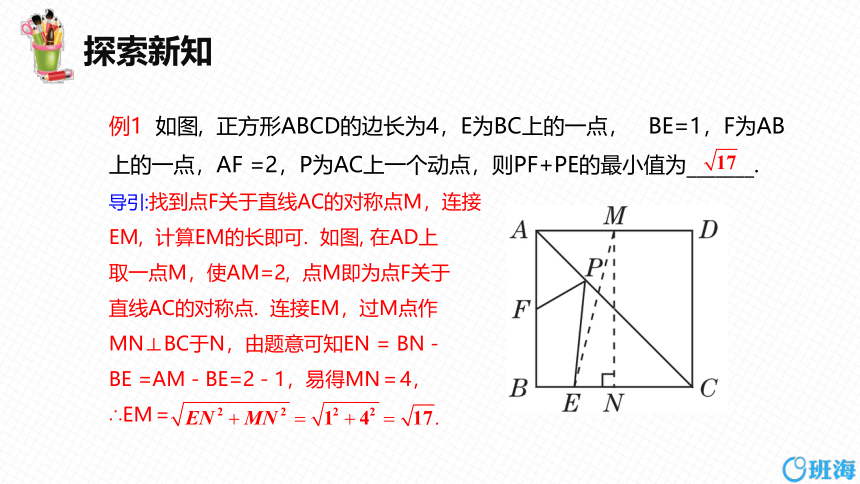
例1 如图, 正方形ABCD的边长为4,E为BC上的一点, BE=1,F为AB上的一点,AF =2,P为AC上一个动点,则PF+PE的最小值为_______.
导引:找到点F关于直线AC的对称点M,连接
EM, 计算EM的长即可. 如图, 在AD上
取一点M,使AM=2, 点M即为点F关于
直线AC的对称点. 连接EM,过M点作
MN⊥BC于N,由题意可知EN = BN-
BE =AM-BE=2-1,易得MN=4,
∴EM=
探索新知
总 结
正方形是特殊的平行四边形,正方形关于它的
对角线所在直线对称. 求两线段和的最小值,往往
要通过轴对称的方式将同侧两点转化为异侧两点,
通过两点间线段最短求得两线段和的最小值.
探索新知
2
知识点
正方形的判定
议一议
满足什么条件的矩形是正方形?满足什么条件的菱形是正方形?请证明你的结论,并与同伴交流.
探索新知
1.正方形的判定定理:
(1)定理1:对角线相等的菱形是正方形.
(2)定理2:对角线垂直的矩形是正方形.
(3)定理3:有一个角是直角的菱形是正方形.
(4)定理4:有一组邻边相等的矩形是正方形.
请你证明以上定理.
探索新知
2.判定方法:
(1)从四边形出发:①有四条边相等,四个角都是直角的四边形是
正方形;②对角线互相平分、垂直且相等的四边形是正方形.
(2)从平行四边形出发:①有一组邻边相等并且有一个角是直角的
平行四边形是正方形;②对角线互相垂直且相等的平行四边形
是正方形.
(3)从矩形出发:①有一组邻边相等的矩形是正方形;②对角线互
相垂直的矩形是正方形.
(4)从菱形出发:①有一个角是直角的菱形是正方形;②对角线相
等的菱形是正方形.
探索新知
例2 已知:如图,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE.求证:四边形BECF是正方形.
证明:
∵BF∥CE,CF∥BE,
∴四边形BECF是平行四边形.
∵四边形ABCD是矩形,
∴∠ABC=90°,∠DCB=90°.
又∵BE平分∠ABC,CE平分∠DCB,
∴∠EBC= ∠ABC=45°,∠ECB= ∠DCB=45°.
∴∠EBC=∠ECB. ∴EB=EC.
探索新知
∴ BECF是菱形(菱形的定义).
在△EBC中,
∵∠EBC=45°,∠ECB=45°,
∴∠BEC=90°.
∴菱形BECF是正方形(有一个角是直角的菱形是
正方形).
典题精讲
1
如图,在菱形ABCD中,对角线AC,BD相交于点O,
不添加任何辅助线,请添加一个条件_____________
_____________,使四边形ABCD是正方形.(填一个即可)
∠BAD=90°
(答案不唯一)
典题精讲
2
在△ABC中,点D,E,F分别在BC,AB,CA上,且DE∥CA,DF∥BA,连接EF,则下列三种说法:
①如果EF=AD,那么四边形AEDF是矩形;
②如果EF⊥AD,那么四边形AEDF是菱形;
③如果AD⊥BC且AB=AC,那么四边形AEDF是正方形,其中正确的有( )
A.3个 B.2个 C.1个 D.0个
B
学以致用
小试牛刀
1.正方形是________对称图形,它有______条对称轴.若正方形的边长为A,则它的对角线长为________,面积为________.
轴
4
a
a2
2.如图,正方形ABCD的边长为4 cm,则图中阴影部分的面积为________.
8 cm2
小试牛刀
3.如图,菱形ABCD的面积为120 cm2,正方形AECF的面积为50 cm2,
则菱形的边长为________.
13 cm
4.在 ABCD中,对角线AC与BD相交于点O,要使四边形ABCD是正方形,还需添加一组条件.下面给出了四组条件:①AB⊥AD,且AB=AD;②AB=BD,且AB⊥BD;③OB=OC,且OB⊥OC;④AB=AD,且AC=BD.其中正确的序号是________.
①③④
小试牛刀
具体判定方法如下:
对角线互相垂直的________是正方形;
对角线相等的________是正方形;
对角线互相垂直且相等的____________是正方形;
有一个角是直角的________是正方形;
有一组邻边相等的________是正方形.
矩形
菱形
平行四边形
菱形
矩形
5.判定一个四边形是正方形,就要判定它既是______,又是________.
矩形
菱形
小试牛刀
6.如图,点E在正方形ABCD的对角线AC上,E为AC的中点,Rt△FEG的两条直角边EF,EG分别交BC,DC于点M,N.若正方形ABCD的边长为a,则阴影部分即四边形EMCN的面积为( )
A. a2 B. a2
C. a2 D. a2
B
小试牛刀
7.小红用次数最少的对折方法验证了一条四边形丝巾的形状是正方形,她对折了( )
A.1次 B.2次 C.3次 D.4次
B
8.将五个边长都为2 cm的正方形按如图所示摆放,点A,B,C,D分别是四个正方形的中心,则图中四块阴影部分面积的和为( )
A.2 cm2 B.4 cm2
C.6 cm2 D.8 cm2
B
小试牛刀
9.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,连接CE,CF,添加一个条件,仍不能证明四边形BECF为正方形的是( )
A.BC=AC B.CF⊥BF
C.BD=DF D.AC=BF
D
小试牛刀
10.已知:如图,在四边形ABCD中,AD∥BC,AD=CD,E是对角
线BD上一点,且EA=EC.
(1)求证:四边形ABCD是菱形;
在△ADE与△CDE中,
AD=CD,
DE=DE,
EA=EC,
∴△ADE≌△CDE.
∴∠ADE=∠CDE.
证明:
∵AD∥BC,∴∠ADE=∠CBD.
∴∠CDE=∠CBD.∴BC=CD.
∵AD=CD,∴BC=AD.
∴四边形ABCD为平行四边形.
∵AD=CD,∴四边形ABCD是菱形.
小试牛刀
(2)如果BE=BC,且∠CBE∶∠BCE=2∶3,求证:四边形ABCD是正方形.
∵BE=BC,∴∠BCE=∠BEC.
∵∠CBE?∠BCE=2?3,
∴∠CBE=180°× =45°.
∵四边形ABCD是菱形,
∴∠ABE=45°.∴∠ABC=90°.
∴四边形ABCD是正方形.
证明:
课堂小结
课堂小结
正方形的判定:
平行四边形
矩形
菱形
正方形
一组邻边相等
一个内角是直角
一组邻边相等
对角线垂直
对角线相等
一个内角为直角
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
1.3 正方形的性质与判定
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图,将一张长方形纸对折两次,然后剪下一个角,打开.怎样剪才能剪出一个正方形?
新课精讲
探索新知
1
知识点
正方形的对称性
正方形:既是中心对称图形,又是轴对称图形.它的中心是对称中心,有4条对称轴,分别是两条对角线和每组对边中点连线所在直线.
探索新知
知识点
例1 如图, 正方形ABCD的边长为4,E为BC上的一点, BE=1,F为AB上的一点,AF =2,P为AC上一个动点,则PF+PE的最小值为_______.
导引:找到点F关于直线AC的对称点M,连接
EM, 计算EM的长即可. 如图, 在AD上
取一点M,使AM=2, 点M即为点F关于
直线AC的对称点. 连接EM,过M点作
MN⊥BC于N,由题意可知EN = BN-
BE =AM-BE=2-1,易得MN=4,
∴EM=
探索新知
总 结
正方形是特殊的平行四边形,正方形关于它的
对角线所在直线对称. 求两线段和的最小值,往往
要通过轴对称的方式将同侧两点转化为异侧两点,
通过两点间线段最短求得两线段和的最小值.
探索新知
2
知识点
正方形的判定
议一议
满足什么条件的矩形是正方形?满足什么条件的菱形是正方形?请证明你的结论,并与同伴交流.
探索新知
1.正方形的判定定理:
(1)定理1:对角线相等的菱形是正方形.
(2)定理2:对角线垂直的矩形是正方形.
(3)定理3:有一个角是直角的菱形是正方形.
(4)定理4:有一组邻边相等的矩形是正方形.
请你证明以上定理.
探索新知
2.判定方法:
(1)从四边形出发:①有四条边相等,四个角都是直角的四边形是
正方形;②对角线互相平分、垂直且相等的四边形是正方形.
(2)从平行四边形出发:①有一组邻边相等并且有一个角是直角的
平行四边形是正方形;②对角线互相垂直且相等的平行四边形
是正方形.
(3)从矩形出发:①有一组邻边相等的矩形是正方形;②对角线互
相垂直的矩形是正方形.
(4)从菱形出发:①有一个角是直角的菱形是正方形;②对角线相
等的菱形是正方形.
探索新知
例2 已知:如图,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE.求证:四边形BECF是正方形.
证明:
∵BF∥CE,CF∥BE,
∴四边形BECF是平行四边形.
∵四边形ABCD是矩形,
∴∠ABC=90°,∠DCB=90°.
又∵BE平分∠ABC,CE平分∠DCB,
∴∠EBC= ∠ABC=45°,∠ECB= ∠DCB=45°.
∴∠EBC=∠ECB. ∴EB=EC.
探索新知
∴ BECF是菱形(菱形的定义).
在△EBC中,
∵∠EBC=45°,∠ECB=45°,
∴∠BEC=90°.
∴菱形BECF是正方形(有一个角是直角的菱形是
正方形).
典题精讲
1
如图,在菱形ABCD中,对角线AC,BD相交于点O,
不添加任何辅助线,请添加一个条件_____________
_____________,使四边形ABCD是正方形.(填一个即可)
∠BAD=90°
(答案不唯一)
典题精讲
2
在△ABC中,点D,E,F分别在BC,AB,CA上,且DE∥CA,DF∥BA,连接EF,则下列三种说法:
①如果EF=AD,那么四边形AEDF是矩形;
②如果EF⊥AD,那么四边形AEDF是菱形;
③如果AD⊥BC且AB=AC,那么四边形AEDF是正方形,其中正确的有( )
A.3个 B.2个 C.1个 D.0个
B
学以致用
小试牛刀
1.正方形是________对称图形,它有______条对称轴.若正方形的边长为A,则它的对角线长为________,面积为________.
轴
4
a
a2
2.如图,正方形ABCD的边长为4 cm,则图中阴影部分的面积为________.
8 cm2
小试牛刀
3.如图,菱形ABCD的面积为120 cm2,正方形AECF的面积为50 cm2,
则菱形的边长为________.
13 cm
4.在 ABCD中,对角线AC与BD相交于点O,要使四边形ABCD是正方形,还需添加一组条件.下面给出了四组条件:①AB⊥AD,且AB=AD;②AB=BD,且AB⊥BD;③OB=OC,且OB⊥OC;④AB=AD,且AC=BD.其中正确的序号是________.
①③④
小试牛刀
具体判定方法如下:
对角线互相垂直的________是正方形;
对角线相等的________是正方形;
对角线互相垂直且相等的____________是正方形;
有一个角是直角的________是正方形;
有一组邻边相等的________是正方形.
矩形
菱形
平行四边形
菱形
矩形
5.判定一个四边形是正方形,就要判定它既是______,又是________.
矩形
菱形
小试牛刀
6.如图,点E在正方形ABCD的对角线AC上,E为AC的中点,Rt△FEG的两条直角边EF,EG分别交BC,DC于点M,N.若正方形ABCD的边长为a,则阴影部分即四边形EMCN的面积为( )
A. a2 B. a2
C. a2 D. a2
B
小试牛刀
7.小红用次数最少的对折方法验证了一条四边形丝巾的形状是正方形,她对折了( )
A.1次 B.2次 C.3次 D.4次
B
8.将五个边长都为2 cm的正方形按如图所示摆放,点A,B,C,D分别是四个正方形的中心,则图中四块阴影部分面积的和为( )
A.2 cm2 B.4 cm2
C.6 cm2 D.8 cm2
B
小试牛刀
9.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,连接CE,CF,添加一个条件,仍不能证明四边形BECF为正方形的是( )
A.BC=AC B.CF⊥BF
C.BD=DF D.AC=BF
D
小试牛刀
10.已知:如图,在四边形ABCD中,AD∥BC,AD=CD,E是对角
线BD上一点,且EA=EC.
(1)求证:四边形ABCD是菱形;
在△ADE与△CDE中,
AD=CD,
DE=DE,
EA=EC,
∴△ADE≌△CDE.
∴∠ADE=∠CDE.
证明:
∵AD∥BC,∴∠ADE=∠CBD.
∴∠CDE=∠CBD.∴BC=CD.
∵AD=CD,∴BC=AD.
∴四边形ABCD为平行四边形.
∵AD=CD,∴四边形ABCD是菱形.
小试牛刀
(2)如果BE=BC,且∠CBE∶∠BCE=2∶3,求证:四边形ABCD是正方形.
∵BE=BC,∴∠BCE=∠BEC.
∵∠CBE?∠BCE=2?3,
∴∠CBE=180°× =45°.
∵四边形ABCD是菱形,
∴∠ABE=45°.∴∠ABC=90°.
∴四边形ABCD是正方形.
证明:
课堂小结
课堂小结
正方形的判定:
平行四边形
矩形
菱形
正方形
一组邻边相等
一个内角是直角
一组邻边相等
对角线垂直
对角线相等
一个内角为直角
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
