北师大版(新)九上-1.3 正方形的性质与判定 第三课时【优质课件】
文档属性
| 名称 | 北师大版(新)九上-1.3 正方形的性质与判定 第三课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览










文档简介
(共34张PPT)
1.3 正方形的性质与判定
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课前导入
情景导入
正方形是________对称图形,它有______条对称轴.若正方形的边长为A,则它的对角线长为________,面积为________.
轴
4
a
a2
回顾旧知
新课精讲
探索新知
1.如图,在正方形ABCD中,对角线AC,BD相交于点O,E,F分别在OD,OC上,且DE=CF,连接DF,AE,并延长AE交DF
于点M.求证:AM⊥DF.
1
类型
利用正方形的性质证明线段位置关系
探索新知
∵AC,BD是正方形ABCD的两条对角线,
∴AC⊥BD,OA=OD=OC=OB.∵DE=CF,
∴OE=OF.在△AOE与△DOF中,
OA=OD,
∠AOE=∠DOF=90°,
OE=OF,
∴△AOE≌△DOF.
证明:
探索新知
∴∠OAE=∠ODF.
∵∠DOF=90°,
∴∠DFO+∠FDO=90°.
∴∠DFO+∠FAE=90°.
∴∠AMF=90°,即AM⊥DF.
探索新知
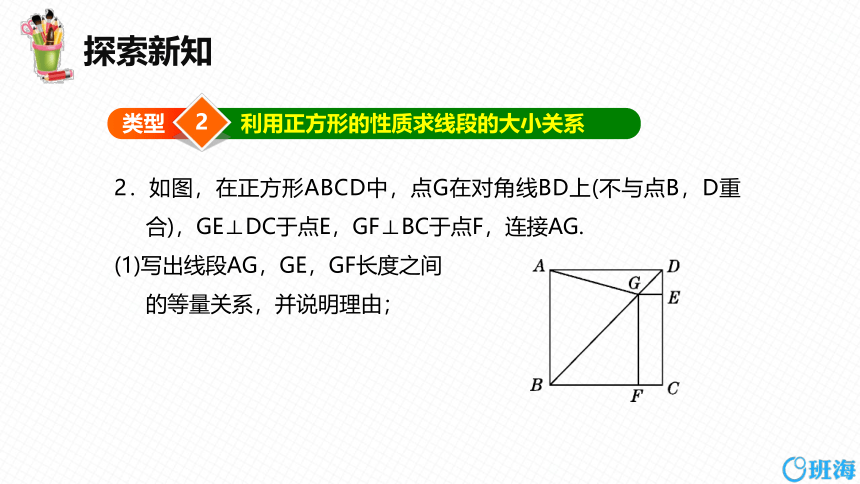
2.如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连接AG.
(1)写出线段AG,GE,GF长度之间
的等量关系,并说明理由;
2
类型
利用正方形的性质求线段的大小关系
探索新知
AG2=GE2+GF2.理由如下:
如图,连接GC,由正方形的性质知AD=CD,
∠ADG=∠CDG.在△ADG和△CDG中,
AD=CD,
∠ADG=∠CDG,
GD=GD,
所以△ADG≌△CDG.
探索新知
所以AG=CG.
由题意知∠GEC=∠GFC=∠DCB=90°.
所以四边形GFCE为矩形,
CG2=CF2+GF2.所以GE=FC.
又因为AG=CG,
所以AG2=GE2+GF2.
探索新知
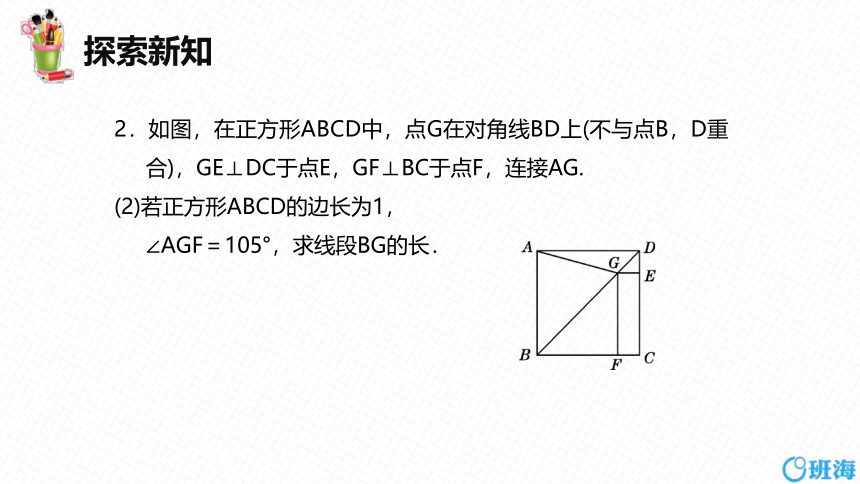
2.如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连接AG.
(2)若正方形ABCD的边长为1,
∠AGF=105°,求线段BG的长.
探索新知
如图,作AH⊥BD于点H,由题意易知∠AGB=60°,∠ABG=45°,所以∠BAH=45°=∠ABG,
∠GAH=30°.所以AH=BH,AG=2HG.
因为AB=1,所以在Rt△ABH中,
由勾股定理可得AH=BH= .
在Rt△AGH中,由勾股定理可得
HG= .所以BG= .
探索新知
3.如图,在正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.
3
类型
利用正方形的性质解决相关问题
探索新知
下列结论:
①△ABG≌△AFG; ②BG=GC;
③EG=DE+BG; ④AG∥CF;
⑤S△FGC=3.6.
其中正确结论的个数是( )
A.2 B.3 C.4 D.5
D
探索新知
4.如图,P,Q,R,S四个小球分别从正方形的四个顶点A,B,C,D同时出发,以同样的速度分别沿AB,BC,CD,DA的方向滚动,
其终点分别是B,C,D,A.
(1)不管滚动多长时间,求证:连接四
个小球所得的四边形PQRS总是正方形;
4
类型
正方形性质与判定的综合运用
探索新知
∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA.
又∵在任何运动时刻,AP=BQ=CR=DS,
∴PB=QC=RD=SA.
∴△ASP≌△BPQ≌△CQR≌△DRS.
∴PS=QP=RQ=SR,∠ASP=∠BPQ.
∴在任何运动时刻,四边形PQRS是菱形.
证明:
探索新知
又∵∠APS+∠ASP=90°,
∴∠APS+∠BPQ=90°.
∴∠QPS=180°-(∠APS+∠BPQ)
=180°-90°=90°.
∴在任何运动时刻,四边形PQRS总是正方形.
探索新知
4.如图,P,Q,R,S四个小球分别从正方形的四个顶点A,B,C,D同时出发,以同样的速度分别沿AB,BC,CD,DA的方向滚动,
其终点分别是B,C,D,A.
(2)四边形PQRS在什么时候面积最大?
当P,Q,R,S在出发时或在到达终点时面积最大,此时的面积就等于原正方形ABCD的面积.
解:
学以致用
小试牛刀
1.下列命题中,真命题是( )
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线互相平分的四边形是平行四边形
D.对角线互相垂直平分的四边形是正方形
C
小试牛刀
2.关于 ABCD的叙述,正确的是 ( )
A.若AB⊥BC,则 ABCD是菱形
B.若AC⊥BD,则 ABCD是正方形
C.若AC=BD,则 ABCD是矩形
D.若AB=AD,则 ABCD是正方形
C
小试牛刀
3.如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,连接EF,交AD于O,则下列结论:
①OA=OD;②AD⊥EF;
③AE+DF=AF+DE;
④当∠BAC=90°时,四边形AEDF是正方形.其中一定正确的是( )
A.①②③ B.②③④ C.①③④ D.①②③④
B
小试牛刀
4.如图,△ABC是等腰直角三角形,∠BAC=90°,点P,Q分别是AB,AC上的动点,
且满足BP=AQ,D是BC的中点.
(1)求证:△PDQ是等腰直角三角形.
连接AD,
∵△ABC是等腰直角三角形,
∠BAC=90°,D是BC的中点,
∴AD⊥BC,AD=BD=DC,
∠DAQ=∠B=45°.
在△BPD和△AQD中,
证明:
小试牛刀
∵BD=AD,∠B=∠DAQ,BP=AQ,
∴△BPD≌△AQD.
∴PD=QD,∠ADQ=∠BDP.
∵∠BDP+∠ADP=90°,
∴∠ADP+∠ADQ=90°,
即∠PDQ=90°. ∴△PDQ是等腰直角三角形.
小试牛刀
5.如图,△ABC是等腰直角三角形,∠BAC=90°,点P,Q分别是AB,AC上的动点,且满足BP=AQ,D是BC的中点.
(2)当点P运动到什么位置时,
四边形APDQ是正
方形?请说明理由.
小试牛刀
当点P运动到AB的中点时,四边形APDQ是正方形.
理由:由(1)知,AD⊥BC,AD=BD,
∴△ABD是等腰直角三角形.当P为AB的中点时,PD⊥AB,即∠APD=90°,
又∠BAC=∠PDQ=90°,∴四边形APDQ是矩形.
又PD=QD, ∴四边形APDQ是正方形.
解:
小试牛刀
6.定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图①,等腰直角四边形ABCD,
AB=BC,∠ABC=90°.
①若AB=CD=1,AB∥CD,求对角线BD的长;
②若AC⊥BD,求证:AD=CD.
小试牛刀
∵AB=CD=1,AB∥CD,
∴四边形ABCD是平行四边形.
又∵AB=BC,∴四边形ABCD是菱形.
又∵∠ABC=90°,
∴四边形ABCD是正方形.
∴BD= .
①解:
小试牛刀
如图①,连接AC,BD,
∵AB=BC,AC⊥BD,
∴∠ABD=∠CBD.
又∵BD=BD,
∴△ABD≌△CBD.
∴AD=CD.
②证明:
小试牛刀
(2)如图②,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交AD,BC于点E,F,使四边形ABFE是等腰直
角四边形,求AE的长.
(提示:在形如 的图形中,
若AB∥CD,则 )
小试牛刀
若EF与BC垂直,则AE≠EF,BF≠EF,
AB≠BF,AB≠AE,
∴四边形ABFE不是等腰直角四边形,不符合条件.
若EF与BC不垂直.
①当AE=AB=5时,如图②,
此时四边形ABFE是等腰直角四边形.
解:
小试牛刀
②当BF=AB时,如图③,此时四边形ABFE是等腰直角四边形.
∴BF=AB=5.∵DE∥BF,
∴DE∶BF=PD∶PB=1∶2.
∴DE=2.5. ∴AE=9-2.5=6.5.
综上所述,AE的长为5或6.5.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
1.3 正方形的性质与判定
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课前导入
情景导入
正方形是________对称图形,它有______条对称轴.若正方形的边长为A,则它的对角线长为________,面积为________.
轴
4
a
a2
回顾旧知
新课精讲
探索新知
1.如图,在正方形ABCD中,对角线AC,BD相交于点O,E,F分别在OD,OC上,且DE=CF,连接DF,AE,并延长AE交DF
于点M.求证:AM⊥DF.
1
类型
利用正方形的性质证明线段位置关系
探索新知
∵AC,BD是正方形ABCD的两条对角线,
∴AC⊥BD,OA=OD=OC=OB.∵DE=CF,
∴OE=OF.在△AOE与△DOF中,
OA=OD,
∠AOE=∠DOF=90°,
OE=OF,
∴△AOE≌△DOF.
证明:
探索新知
∴∠OAE=∠ODF.
∵∠DOF=90°,
∴∠DFO+∠FDO=90°.
∴∠DFO+∠FAE=90°.
∴∠AMF=90°,即AM⊥DF.
探索新知
2.如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连接AG.
(1)写出线段AG,GE,GF长度之间
的等量关系,并说明理由;
2
类型
利用正方形的性质求线段的大小关系
探索新知
AG2=GE2+GF2.理由如下:
如图,连接GC,由正方形的性质知AD=CD,
∠ADG=∠CDG.在△ADG和△CDG中,
AD=CD,
∠ADG=∠CDG,
GD=GD,
所以△ADG≌△CDG.
探索新知
所以AG=CG.
由题意知∠GEC=∠GFC=∠DCB=90°.
所以四边形GFCE为矩形,
CG2=CF2+GF2.所以GE=FC.
又因为AG=CG,
所以AG2=GE2+GF2.
探索新知
2.如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连接AG.
(2)若正方形ABCD的边长为1,
∠AGF=105°,求线段BG的长.
探索新知
如图,作AH⊥BD于点H,由题意易知∠AGB=60°,∠ABG=45°,所以∠BAH=45°=∠ABG,
∠GAH=30°.所以AH=BH,AG=2HG.
因为AB=1,所以在Rt△ABH中,
由勾股定理可得AH=BH= .
在Rt△AGH中,由勾股定理可得
HG= .所以BG= .
探索新知
3.如图,在正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.
3
类型
利用正方形的性质解决相关问题
探索新知
下列结论:
①△ABG≌△AFG; ②BG=GC;
③EG=DE+BG; ④AG∥CF;
⑤S△FGC=3.6.
其中正确结论的个数是( )
A.2 B.3 C.4 D.5
D
探索新知
4.如图,P,Q,R,S四个小球分别从正方形的四个顶点A,B,C,D同时出发,以同样的速度分别沿AB,BC,CD,DA的方向滚动,
其终点分别是B,C,D,A.
(1)不管滚动多长时间,求证:连接四
个小球所得的四边形PQRS总是正方形;
4
类型
正方形性质与判定的综合运用
探索新知
∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA.
又∵在任何运动时刻,AP=BQ=CR=DS,
∴PB=QC=RD=SA.
∴△ASP≌△BPQ≌△CQR≌△DRS.
∴PS=QP=RQ=SR,∠ASP=∠BPQ.
∴在任何运动时刻,四边形PQRS是菱形.
证明:
探索新知
又∵∠APS+∠ASP=90°,
∴∠APS+∠BPQ=90°.
∴∠QPS=180°-(∠APS+∠BPQ)
=180°-90°=90°.
∴在任何运动时刻,四边形PQRS总是正方形.
探索新知
4.如图,P,Q,R,S四个小球分别从正方形的四个顶点A,B,C,D同时出发,以同样的速度分别沿AB,BC,CD,DA的方向滚动,
其终点分别是B,C,D,A.
(2)四边形PQRS在什么时候面积最大?
当P,Q,R,S在出发时或在到达终点时面积最大,此时的面积就等于原正方形ABCD的面积.
解:
学以致用
小试牛刀
1.下列命题中,真命题是( )
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线互相平分的四边形是平行四边形
D.对角线互相垂直平分的四边形是正方形
C
小试牛刀
2.关于 ABCD的叙述,正确的是 ( )
A.若AB⊥BC,则 ABCD是菱形
B.若AC⊥BD,则 ABCD是正方形
C.若AC=BD,则 ABCD是矩形
D.若AB=AD,则 ABCD是正方形
C
小试牛刀
3.如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,连接EF,交AD于O,则下列结论:
①OA=OD;②AD⊥EF;
③AE+DF=AF+DE;
④当∠BAC=90°时,四边形AEDF是正方形.其中一定正确的是( )
A.①②③ B.②③④ C.①③④ D.①②③④
B
小试牛刀
4.如图,△ABC是等腰直角三角形,∠BAC=90°,点P,Q分别是AB,AC上的动点,
且满足BP=AQ,D是BC的中点.
(1)求证:△PDQ是等腰直角三角形.
连接AD,
∵△ABC是等腰直角三角形,
∠BAC=90°,D是BC的中点,
∴AD⊥BC,AD=BD=DC,
∠DAQ=∠B=45°.
在△BPD和△AQD中,
证明:
小试牛刀
∵BD=AD,∠B=∠DAQ,BP=AQ,
∴△BPD≌△AQD.
∴PD=QD,∠ADQ=∠BDP.
∵∠BDP+∠ADP=90°,
∴∠ADP+∠ADQ=90°,
即∠PDQ=90°. ∴△PDQ是等腰直角三角形.
小试牛刀
5.如图,△ABC是等腰直角三角形,∠BAC=90°,点P,Q分别是AB,AC上的动点,且满足BP=AQ,D是BC的中点.
(2)当点P运动到什么位置时,
四边形APDQ是正
方形?请说明理由.
小试牛刀
当点P运动到AB的中点时,四边形APDQ是正方形.
理由:由(1)知,AD⊥BC,AD=BD,
∴△ABD是等腰直角三角形.当P为AB的中点时,PD⊥AB,即∠APD=90°,
又∠BAC=∠PDQ=90°,∴四边形APDQ是矩形.
又PD=QD, ∴四边形APDQ是正方形.
解:
小试牛刀
6.定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图①,等腰直角四边形ABCD,
AB=BC,∠ABC=90°.
①若AB=CD=1,AB∥CD,求对角线BD的长;
②若AC⊥BD,求证:AD=CD.
小试牛刀
∵AB=CD=1,AB∥CD,
∴四边形ABCD是平行四边形.
又∵AB=BC,∴四边形ABCD是菱形.
又∵∠ABC=90°,
∴四边形ABCD是正方形.
∴BD= .
①解:
小试牛刀
如图①,连接AC,BD,
∵AB=BC,AC⊥BD,
∴∠ABD=∠CBD.
又∵BD=BD,
∴△ABD≌△CBD.
∴AD=CD.
②证明:
小试牛刀
(2)如图②,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交AD,BC于点E,F,使四边形ABFE是等腰直
角四边形,求AE的长.
(提示:在形如 的图形中,
若AB∥CD,则 )
小试牛刀
若EF与BC垂直,则AE≠EF,BF≠EF,
AB≠BF,AB≠AE,
∴四边形ABFE不是等腰直角四边形,不符合条件.
若EF与BC不垂直.
①当AE=AB=5时,如图②,
此时四边形ABFE是等腰直角四边形.
解:
小试牛刀
②当BF=AB时,如图③,此时四边形ABFE是等腰直角四边形.
∴BF=AB=5.∵DE∥BF,
∴DE∶BF=PD∶PB=1∶2.
∴DE=2.5. ∴AE=9-2.5=6.5.
综上所述,AE的长为5或6.5.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
