北师大版(新)九上-1.3 正方形的性质与判定 第一课时【优质课件】
文档属性
| 名称 | 北师大版(新)九上-1.3 正方形的性质与判定 第一课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:52:22 | ||
图片预览








文档简介
(共35张PPT)
1.1 正数和负数
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
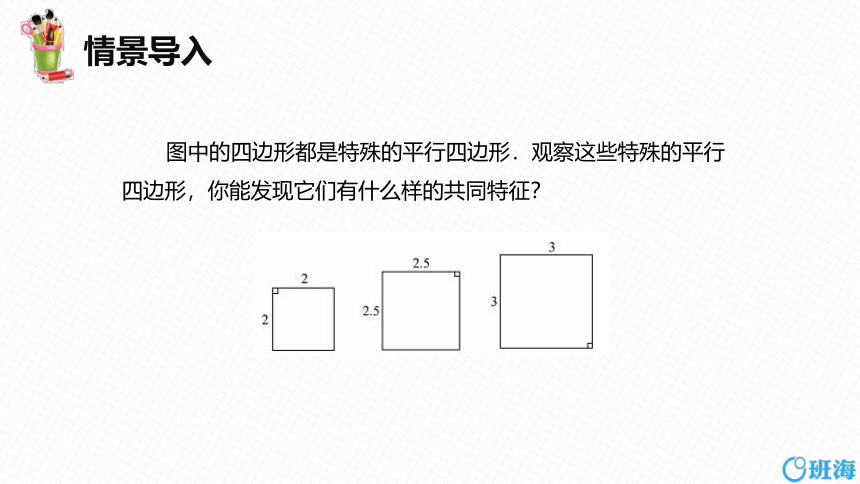
图中的四边形都是特殊的平行四边形.观察这些特殊的平行四边形,你能发现它们有什么样的共同特征?
新课精讲
探索新知
1
知识点
正方形的定义
正方形的定义:
有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形.
典题精讲
下面四个定义中不正确的是( )
A.有一个角是直角的平行四边形叫做矩形
B.有一组邻边相等的四边形叫做菱形
C.有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形
D.有一组邻边相等的平行四边形叫做菱形
B
探索新知
2
知识点
正方形的性质
议一议
(1)正方形是矩形吗?是菱形吗?
(2)你认为正方形的边具有哪些性质?与同伴交流.正方形既是矩形,又是菱形,它具有矩形与菱形的所有性质.
正方形的性质:
具有矩形、菱形、平行四边形的一切性质,即四条边相等,邻边垂直,对边平行;
探索新知
知识点
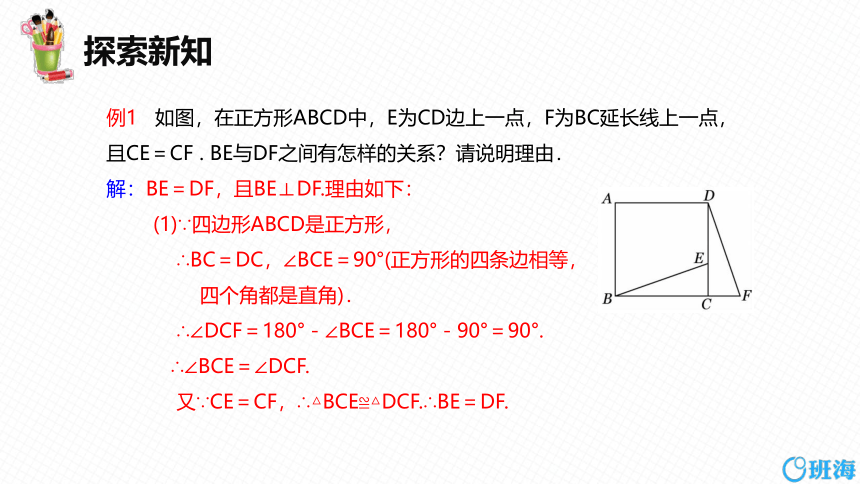
例1 如图,在正方形ABCD中,E为CD边上一点,F为BC延长线上一点,且CE=CF . BE与DF之间有怎样的关系?请说明理由.
解:BE=DF,且BE⊥DF.理由如下:
(1)∵四边形ABCD是正方形,
∴BC=DC,∠BCE=90°(正方形的四条边相等,
四个角都是直角).
∴∠DCF=180°-∠BCE=180°-90°=90°.
∴∠BCE=∠DCF.
又∵CE=CF,∴△BCE≌△DCF.∴BE=DF.
探索新知
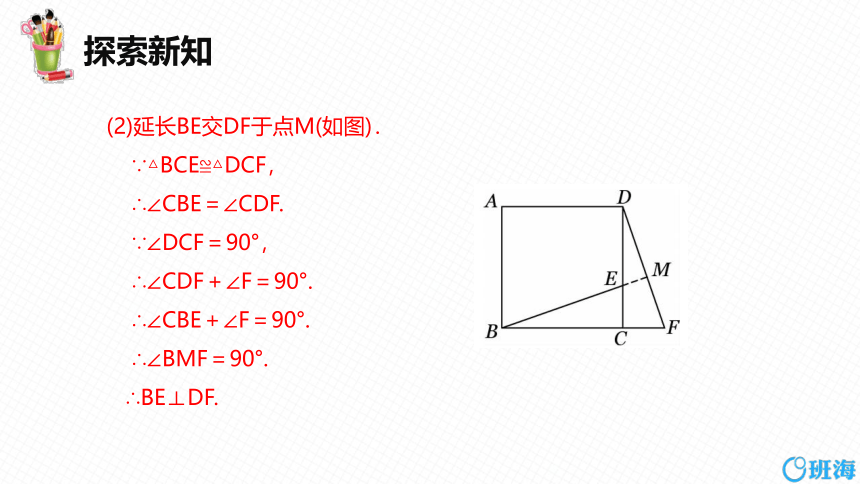
(2)延长BE交DF于点M(如图).
∵△BCE≌△DCF,
∴∠CBE=∠CDF.
∵∠DCF=90°,
∴∠CDF+∠F=90°.
∴∠CBE+∠F=90°.
∴∠BMF=90°.
∴BE⊥DF.
探索新知
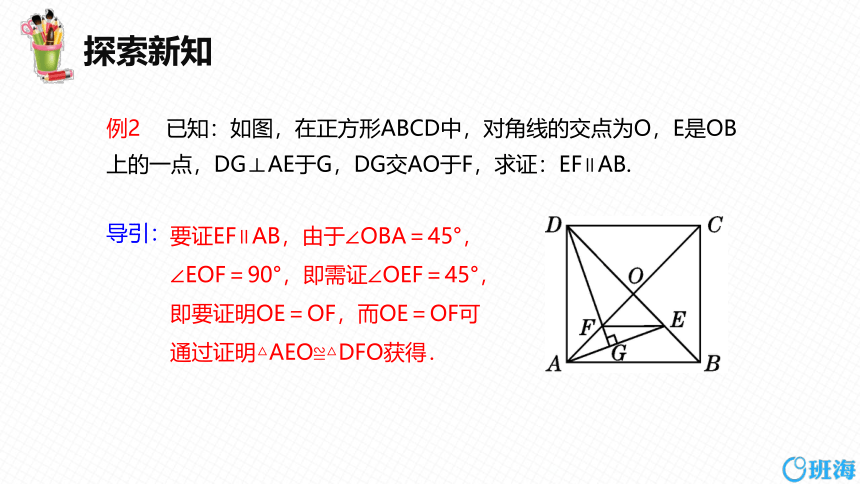
例2 已知:如图,在正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交AO于F,求证:EF∥AB.
要证EF∥AB,由于∠OBA=45°,
∠EOF=90°,即需证∠OEF=45°,
即要证明OE=OF,而OE=OF可
通过证明△AEO≌△DFO获得.
导引:
探索新知
∵四边形ABCD是正方形,
∴∠AOE=∠DOF=90°,AO=DO,∠OBA=45°.
又∵DG⊥AE,
∴∠EAO+∠AEO=∠EDG+∠GED=90°.
∵∠AEO=∠GED,∴∠EAO=∠EDG=∠FDO.
∴△AEO≌△DFO(ASA).∴OE=OF.
∴∠OEF=45°. ∴∠OEF=∠OBA.
∴EF∥AB.
证明:
探索新知
总 结
通过证明三角形全等得到边和角相等,再进一步得到平行或垂直,是有关正方形中证边或角相等的最常用的方法,而正方形的四条边相等,四个角都是直角为证明三角形全等提供了条件.
探索新知
知识点
议一议
平行四边形、菱形、矩形、正方形之间有什么关系?你能用一个图直观地表示它们之间的关系吗?与同伴交流.
平行四边形
矩形
菱形
正方形
解:
典题精讲
1 正方形具有而矩形不一定具有的性质是( )
A.四个角都相等
B.四条边相等
C.对角线相等
D.对角线互相平分
B
典题精讲
2
如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH. 若BE∶EC=2∶1,则线段CH的长是( )
A.3 B.4
C.5 D.6
B
探索新知
例3 如图,正方形ABCD的边长为1 cm,AC为对角线,AE平分∠BAC,EF⊥AC,求BE的长.
线段BE是Rt△ABE的一边,但由于
AE未知,不能直接用勾股定理求BE,
由条件可证△ABE≌△AFE,问题转
化为求EF的长,结合已知条件易获解.
导引:
(正方形角的性质)
探索新知
∵四边形ABCD为正方形,
∴∠B=90°,∠ACB=45°,AB=BC=1 cm.
∵EF⊥AC,∴∠EFA=∠EFC=90°.
又∵∠ECF=45°,
∴△EFC是等腰直角三角形,∴EF=FC.
∵∠BAE=∠FAE,∠B=∠EFA=90°,AE=AE,
∴△ABE≌△AFE.
∴AB=AF=1 cm,BE=EF,∴FC=BE.
在Rt△ABC中,AC
∴FC=AC-AF=( -1)(cm),∴BE=( -1) cm.
解:
探索新知
总 结
解有关正方形的问题,要充分利用正方形的四边
相等、四角相等、对角线垂直平分且相等等性质,正
方形的性质、等腰直角三角形的特点、勾股定理是解
决正方形的相关证明与计算问题的三把钥匙.
典题精讲
1 如图,在正方形ABCD中,连接BD,点O是BD的中点,若M,N是AD上的两点,连接MO,NO,并分别延长交边BC于M′,N′两点,则图中的全等三角形共有( )
A.2对
B.3对
C.4对
D.5对
C
学以致用
小试牛刀
1.有一组________相等,并且有一个角是________的平行四边形是正方形,因此正方形既是________,又是________.
邻边
直角
菱形
矩形
2.正方形不仅是特殊的平行四边形,而且是特殊的______、特殊的______,因此它具有矩形、菱形的性质.边:四条边都______,对边平行.角:四个角都是______.对角线:对角线_________、____、________,并且每一条对角线平分一组对角.
矩形
菱形
相等
直角
互相平分
垂直
相等
小试牛刀
3.如图,BD为正方形ABCD的对角线,BE平分∠DBC,交DC于点E,延长BC到F,使CF=CE,连接DF.若CE=1 cm,则BF=___________________.
(2+2 ) cm
小试牛刀
4.已知在四边形ABCD中,∠A=∠B=∠C=90°,如果添加一个条件,即可推出该四边形是正方 形,那么这个条件可以是( )
A.∠D=90° B.AB=CD
C.AD=BC D.BC=CD
D
5.下列说法错误的是( )
A.正方形是平行四边形 B.正方形是菱形
C.正方形是矩形 D.菱形和矩形都是正方形
D
小试牛刀
6.一个大矩形按如图方式分割成九个小矩形,且只有标号为①和②的两个小矩形为正方形,在满足条件的所有分割中,若知道九个小矩形中n个小矩形的周长,就一定能算出这个大矩形的面积,则n的最小值是( )
A.3 B.4
C.5 D.6
A
小试牛刀
7.如图,在正方形ABCD的外侧作等边三角形ADE,AC,BE相交于点F,则∠BFC等于( )
A.45° B.55°
C.60° D.75°
C
8.正方形具有而菱形不一定具有的性质是( )
A.对角线互相平分
B.对角线相等
C.对角线互相垂直
D.每条对角线平分一组对角
B
小试牛刀
9.如图是边长为10 cm的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:cm)不正确的是( )
A
小试牛刀
10.我们知道:四边形具有不稳定性.如 图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,则点C的对应点C′的坐标为( )
A.( ,1) B.(2,1)
C.(1, ) D.(2, )
D
小试牛刀
11.如图,四边形ABCD是正方形,E,F分别是AB,AD上的一点,且BF⊥CE,垂足为G. 求证:BE=AF.
∵四边形ABCD是正方形,
∴AB=BC,∠A=∠CBE=90°. ∵BF⊥CE,
∴∠BCE+∠CBG=90°.
∵∠ABF+∠CBG=90°,
∴∠BCE=∠ABF.
证明:
小试牛刀
在△BCE和△ABF中,
∠BCE=∠ABF,
BC=AB,
∠CBE=∠A,
∴△BCE≌△ABF(ASA).
∴BE=AF.
小试牛刀
12.如图,E,F是正方形ABCD的对角线AC上的两点,且AE=CF.
(1)求证:四边形BEDF是菱形;
证明:如图,连接BD交AC于O.
∵四边形ABCD是正方形,
∴OB=OD,OA=OC.
∵AE=CF,
∴OE=OF.
∴四边形BEDF是平行四边形.
∵四边形ABCD是正方形,
∴AC⊥BD.∴四边形BEDF是菱形.
小试牛刀
(2)若正方形的边长为4,AE= ,求菱形BEDF的面积.
解:
课堂小结
课堂小结
正方形同时具备平行四边形,矩形,菱形的所有性质,因此,正方形的四个角都是直角,四条边都相等,对角线互相垂直平分且相等,每一条对角线平分一组对角,正方形是轴对称图形,有四条对称轴.这些性质为证明线段相等、垂直,角相等提供了重要的依据.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
1.1 正数和负数
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
图中的四边形都是特殊的平行四边形.观察这些特殊的平行四边形,你能发现它们有什么样的共同特征?
新课精讲
探索新知
1
知识点
正方形的定义
正方形的定义:
有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形.
典题精讲
下面四个定义中不正确的是( )
A.有一个角是直角的平行四边形叫做矩形
B.有一组邻边相等的四边形叫做菱形
C.有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形
D.有一组邻边相等的平行四边形叫做菱形
B
探索新知
2
知识点
正方形的性质
议一议
(1)正方形是矩形吗?是菱形吗?
(2)你认为正方形的边具有哪些性质?与同伴交流.正方形既是矩形,又是菱形,它具有矩形与菱形的所有性质.
正方形的性质:
具有矩形、菱形、平行四边形的一切性质,即四条边相等,邻边垂直,对边平行;
探索新知
知识点
例1 如图,在正方形ABCD中,E为CD边上一点,F为BC延长线上一点,且CE=CF . BE与DF之间有怎样的关系?请说明理由.
解:BE=DF,且BE⊥DF.理由如下:
(1)∵四边形ABCD是正方形,
∴BC=DC,∠BCE=90°(正方形的四条边相等,
四个角都是直角).
∴∠DCF=180°-∠BCE=180°-90°=90°.
∴∠BCE=∠DCF.
又∵CE=CF,∴△BCE≌△DCF.∴BE=DF.
探索新知
(2)延长BE交DF于点M(如图).
∵△BCE≌△DCF,
∴∠CBE=∠CDF.
∵∠DCF=90°,
∴∠CDF+∠F=90°.
∴∠CBE+∠F=90°.
∴∠BMF=90°.
∴BE⊥DF.
探索新知
例2 已知:如图,在正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交AO于F,求证:EF∥AB.
要证EF∥AB,由于∠OBA=45°,
∠EOF=90°,即需证∠OEF=45°,
即要证明OE=OF,而OE=OF可
通过证明△AEO≌△DFO获得.
导引:
探索新知
∵四边形ABCD是正方形,
∴∠AOE=∠DOF=90°,AO=DO,∠OBA=45°.
又∵DG⊥AE,
∴∠EAO+∠AEO=∠EDG+∠GED=90°.
∵∠AEO=∠GED,∴∠EAO=∠EDG=∠FDO.
∴△AEO≌△DFO(ASA).∴OE=OF.
∴∠OEF=45°. ∴∠OEF=∠OBA.
∴EF∥AB.
证明:
探索新知
总 结
通过证明三角形全等得到边和角相等,再进一步得到平行或垂直,是有关正方形中证边或角相等的最常用的方法,而正方形的四条边相等,四个角都是直角为证明三角形全等提供了条件.
探索新知
知识点
议一议
平行四边形、菱形、矩形、正方形之间有什么关系?你能用一个图直观地表示它们之间的关系吗?与同伴交流.
平行四边形
矩形
菱形
正方形
解:
典题精讲
1 正方形具有而矩形不一定具有的性质是( )
A.四个角都相等
B.四条边相等
C.对角线相等
D.对角线互相平分
B
典题精讲
2
如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH. 若BE∶EC=2∶1,则线段CH的长是( )
A.3 B.4
C.5 D.6
B
探索新知
例3 如图,正方形ABCD的边长为1 cm,AC为对角线,AE平分∠BAC,EF⊥AC,求BE的长.
线段BE是Rt△ABE的一边,但由于
AE未知,不能直接用勾股定理求BE,
由条件可证△ABE≌△AFE,问题转
化为求EF的长,结合已知条件易获解.
导引:
(正方形角的性质)
探索新知
∵四边形ABCD为正方形,
∴∠B=90°,∠ACB=45°,AB=BC=1 cm.
∵EF⊥AC,∴∠EFA=∠EFC=90°.
又∵∠ECF=45°,
∴△EFC是等腰直角三角形,∴EF=FC.
∵∠BAE=∠FAE,∠B=∠EFA=90°,AE=AE,
∴△ABE≌△AFE.
∴AB=AF=1 cm,BE=EF,∴FC=BE.
在Rt△ABC中,AC
∴FC=AC-AF=( -1)(cm),∴BE=( -1) cm.
解:
探索新知
总 结
解有关正方形的问题,要充分利用正方形的四边
相等、四角相等、对角线垂直平分且相等等性质,正
方形的性质、等腰直角三角形的特点、勾股定理是解
决正方形的相关证明与计算问题的三把钥匙.
典题精讲
1 如图,在正方形ABCD中,连接BD,点O是BD的中点,若M,N是AD上的两点,连接MO,NO,并分别延长交边BC于M′,N′两点,则图中的全等三角形共有( )
A.2对
B.3对
C.4对
D.5对
C
学以致用
小试牛刀
1.有一组________相等,并且有一个角是________的平行四边形是正方形,因此正方形既是________,又是________.
邻边
直角
菱形
矩形
2.正方形不仅是特殊的平行四边形,而且是特殊的______、特殊的______,因此它具有矩形、菱形的性质.边:四条边都______,对边平行.角:四个角都是______.对角线:对角线_________、____、________,并且每一条对角线平分一组对角.
矩形
菱形
相等
直角
互相平分
垂直
相等
小试牛刀
3.如图,BD为正方形ABCD的对角线,BE平分∠DBC,交DC于点E,延长BC到F,使CF=CE,连接DF.若CE=1 cm,则BF=___________________.
(2+2 ) cm
小试牛刀
4.已知在四边形ABCD中,∠A=∠B=∠C=90°,如果添加一个条件,即可推出该四边形是正方 形,那么这个条件可以是( )
A.∠D=90° B.AB=CD
C.AD=BC D.BC=CD
D
5.下列说法错误的是( )
A.正方形是平行四边形 B.正方形是菱形
C.正方形是矩形 D.菱形和矩形都是正方形
D
小试牛刀
6.一个大矩形按如图方式分割成九个小矩形,且只有标号为①和②的两个小矩形为正方形,在满足条件的所有分割中,若知道九个小矩形中n个小矩形的周长,就一定能算出这个大矩形的面积,则n的最小值是( )
A.3 B.4
C.5 D.6
A
小试牛刀
7.如图,在正方形ABCD的外侧作等边三角形ADE,AC,BE相交于点F,则∠BFC等于( )
A.45° B.55°
C.60° D.75°
C
8.正方形具有而菱形不一定具有的性质是( )
A.对角线互相平分
B.对角线相等
C.对角线互相垂直
D.每条对角线平分一组对角
B
小试牛刀
9.如图是边长为10 cm的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:cm)不正确的是( )
A
小试牛刀
10.我们知道:四边形具有不稳定性.如 图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,则点C的对应点C′的坐标为( )
A.( ,1) B.(2,1)
C.(1, ) D.(2, )
D
小试牛刀
11.如图,四边形ABCD是正方形,E,F分别是AB,AD上的一点,且BF⊥CE,垂足为G. 求证:BE=AF.
∵四边形ABCD是正方形,
∴AB=BC,∠A=∠CBE=90°. ∵BF⊥CE,
∴∠BCE+∠CBG=90°.
∵∠ABF+∠CBG=90°,
∴∠BCE=∠ABF.
证明:
小试牛刀
在△BCE和△ABF中,
∠BCE=∠ABF,
BC=AB,
∠CBE=∠A,
∴△BCE≌△ABF(ASA).
∴BE=AF.
小试牛刀
12.如图,E,F是正方形ABCD的对角线AC上的两点,且AE=CF.
(1)求证:四边形BEDF是菱形;
证明:如图,连接BD交AC于O.
∵四边形ABCD是正方形,
∴OB=OD,OA=OC.
∵AE=CF,
∴OE=OF.
∴四边形BEDF是平行四边形.
∵四边形ABCD是正方形,
∴AC⊥BD.∴四边形BEDF是菱形.
小试牛刀
(2)若正方形的边长为4,AE= ,求菱形BEDF的面积.
解:
课堂小结
课堂小结
正方形同时具备平行四边形,矩形,菱形的所有性质,因此,正方形的四个角都是直角,四条边都相等,对角线互相垂直平分且相等,每一条对角线平分一组对角,正方形是轴对称图形,有四条对称轴.这些性质为证明线段相等、垂直,角相等提供了重要的依据.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
