北师大版(新)九上-2.1 认识一元二次方程 第一课时【优质课件】
文档属性
| 名称 | 北师大版(新)九上-2.1 认识一元二次方程 第一课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:52:22 | ||
图片预览











文档简介
(共33张PPT)
2.1 认识一元二次方程
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
幼儿园某教室矩形地面的长为8 m,宽为5 m,现准备在地面正中间铺设一块面积为18 m2的地毯,四周未铺地毯的条形区域的宽度都相同,你能求出这个宽度吗?
如果设所求的宽度为x m,
那么你能列出怎样的方程?
观察下面等式:
102+112+122=132+142.
情景导入
你还能找到五个连续整数,使前三个数的平方和等于后两个数的平方和吗?
如果将这五个连续整数中的第一个数设为x,那么怎样用含x的代数式表示其余四个数?根据题意,你能列出怎样的方程?
情景导入
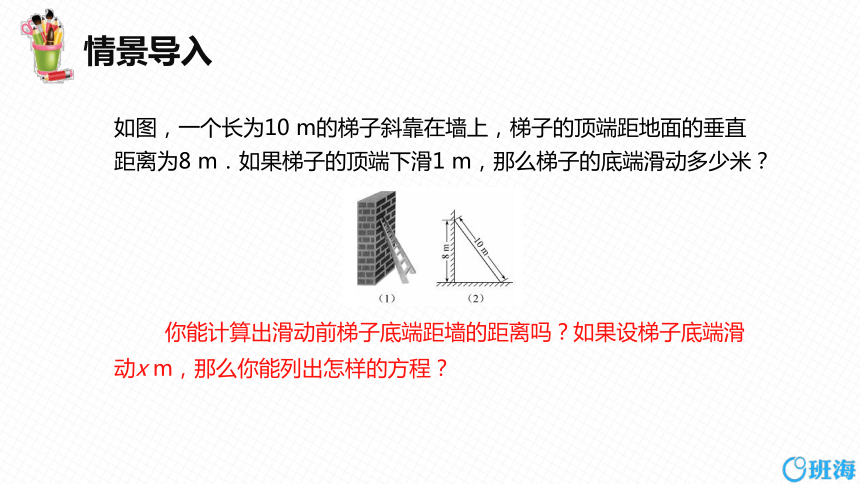
如图,一个长为10 m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8 m.如果梯子的顶端下滑1 m,那么梯子的底端滑动多少米?
你能计算出滑动前梯子底端距墙的距离吗?如果设梯子底端滑动x m,那么你能列出怎样的方程?
新课精讲
探索新知
1
知识点
一元二次方程的定义
议一议
由上面三个问题,我们可以得到三个方程:
(8-2x)(5-2x)=18,
x2+(x+1)2+(x+2)2=(x+3)2+(x+4)2,
(x+6)2+72=102.
这三个方程有什么共同特点?
探索新知
1.定义:只含有一个未知数x的整式方程,并且都可以化成ax2+bx+c=0(a,b,c为常数,a≠0)的形式,这样的方程叫做一元二次方程.
2.一元二次方程的识别方法:整理前是整式方程,且只含一个未知数;整理后未知数的最高次数是2.
探索新知
例1 下列方程:①x2+y-6=0;②x2+ =2;
③x2-x-2=0;④x2-2+5x3-6x=0;
⑤2x2-3x=2(x2-2),是一元二次方程的有( )
A.1个 B. 2个 C.3个 D.4个
A
导引:要判断一个方程是否是一元二次方程,要从原方程及整理后的方程两方面进行判断,看其是否符合一元二次方程的条件.①中有两个未知数;②不是整式方程;④未知数的最高次数是3;⑤整理后二次项系数为零.
探索新知
总 结
一元二次方程的识别方法:
整理前:①整式方程,②只含一个未知数;
整理后:未知数的最高次数是2.
典题精讲
下列关于x的方程一定是一元二次方程的是( )
A.ax2+bx+c=0 B.x2+1-x2=0
C.x2+ =2 D.x2-x-2=0
若方程(m-1)x|m|+1-2x=3是关于x一元二次方程,则( )
A.m=1 B. m=-1
C. m=±1 D.m≠±1
1
2
D
B
探索新知
2
知识点
一元二次方程的一般形式
一般地,任何一个关于x的一元二次方程,经过整理,都能化成如下形式:ax +bx+c=0 (a≠0)这种形式叫做一元二次方程的一般形式 .
探索新知
一元二次方程的项和各项系数
a x +b x+ c =0
二次项系数
一次项系数
a≠0
二次项
一次项
常数项
探索新知
例2 将方程3x(x-1)=5(x+2)化成一元二次方程的一般形式,并写出其中的二次项系数、一次项系数和常数项.
去括号,得3x2-3x=5x+10.
移项,合并同类项,得一元二次方程的一般形式
3x2-8x-10=0.
其中二次项系数为3,一次项系数为-8,常数项为-10.
解:
探索新知
总 结
(1)ax2+bx+c=0,当a≠0时,方程才是一元二次方程,但b,c可以是0.
(2)将一个一元二次方程化成一般形式,可以通过去分母、去括号、移项、合并同类项等步骤.
(3)指出一元二次方程的某项时,应连同未知数一起;指出某项系数时应连同它前面的符号一起.
典题精讲
把方程x(x+2)=5(x-2)化成一般形式,则a,b,c的值分别是( )
A.1,-3,10 B.1,7,-10
C.1,-5,12 D.1,3,2
A
关于x的一元二次方程(m-1)x2+5x+|m|-1=0的常数项为0,则m等于( )
A.1 B.-1
C.1或-1 D.0
B
探索新知
3
知识点
建立一元二次方程的模型
一元二次方程模型:一元二次方程是刻画现实世 界的一个有效数学模型,它是把实际问题中语言叙述的数量关系通过设未知数用一元二次方程来表达.
常用一元二次方程来建模的问题有:图形的面积、增长(利润)率、行程问题、工程问题等.
探索新知
例3 小雨在一幅长90 cm,宽40 cm的油画四周外围镶上一条宽度相同的边框,制成一幅挂图并使油画画面的面积是整个挂图面积 的54%,设边框的宽度为x cm,根据题意,列出方程.
本题涉及两个基本量:油画的面积与整个挂图的面积.
在油画四周外围镶上宽度为x cm的边框,则整个挂图的长与宽各增加了多少?
利用长方形的面积公式和油画面积与整个挂图面积之间的关系列方程
x
90
40
40+2x
90+2x
解:(90+2x)(40+2x)×54%=90×40.
探索新知
总 结
建立一元二次方程模型解决实际问题时,既要根据题目条件中给出的等量关系,又要抓住题目中隐含的一些常用关系式(如面积公式、体积公式、利润公式等)进行列方程.
典题精讲
随州市 “桃花节”观赏人数逐年增加,据有关部门统计,2014年约为20万人次,2016年约为28.8万人次,设观赏人数年均增长率为x,则下列方程中正确的是( )
A.20(1+2x)=28.8
B.28.8(1+x)2=20
C.20(1+x2)=28.8
D. 20+(1+2x)+20(1+x)2=28.8
C
学以致用
小试牛刀
1.等号两边都是整式,只含有____个未知数,并且未知数的最高次数是____的方程,叫做一元二次方程.它具备三个特征:
(1)等式两边都是整式;
(2)只含____个未知数;
(3)未知数的最高次数是____.
一
2
一
2
2.一元二次方程x2-2x=1的一般形式是___________________,二次项系数是___,一次项系数是____,常数项是____.
x2-2x-1=0
1
-2
-1
小试牛刀
3.把一元二次方程(x+1)(1-x)=2x化成二次项系数大于0的一般形式是_________________.
x2+2x-1=0
4.在某次集会中,参加集会的每两人都握了一次手,一共握了66次手,有多少人参加了这次集会?
解:设有x人参加了这次集会,则每人握了_________次手,由于每两人只握一次手,因此总共握了____________次手,列方程得________________________,化成一般形式为_____________________.
(x-1)
x(x-1)
x(x-1)=66
x2-x-132=0
小试牛刀
5.若关于x的方程(a-2)x2-2ax+a+2=0是一元二次方程,则( )
A.a=2 B.a=-2
C.a=0 D.a≠2
D
6.以下是关于x的一元二次方程的是( )
A.x2- =2 B.ax2+bx+c=0
C.3x2-2xy+y2=0 D.(x- )2=0
D
小试牛刀
7.一元二次方程4x2+x=1的二次项系数 一次项系数 常数项分别是( )
A.4,0,1 B.4,1,1 C.4,1,-1 D.4,1,0
C
8.共享单车为市民出行带来了方便.某单车公司第一个月投放1 000辆单车,计划第三个月投放单车数量比第一个月多440辆.设该公司第二 三两个月投放单车数量的月平均增长率为x,则所列方程正确的为( )
A.1 000(1+x)2=1 000+440 B.1 000(1+x)2=440
C.440(1+x)2=1 000 D.1 000(1+2x)=1 000+440
A
小试牛刀
9.如图,某小区计划在一块长为32 m,宽为20 m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570 m2.若设道路的宽为x m,则下面所列方程正确的是( )
A . (32-x)(20-x)=570
B.32x+2×20x=32×20-570
C.(32-x)(20-x)=32×20-570
D.32x+2×20x-2x2=570
A
小试牛刀
10.已知关于x的方程(m2-1)x2-(m+1)x+m=0.
(1)m为何值时,此方程为一元一次方程?
解:若方程为一元一次方程,
∴m=1.
则有
(2)m为何值时,此方程为一元二次方程?并写出一元二次方程的二次项系数 一次项系数及常数项.
若方程为一元二次方程,
则有m2-1≠0,即m≠±1.
二次项系数:m2-1,一次项系数:-(m+1),常数项:m.
小试牛刀
11.若x2a+b-2xa-b+3=0是关于x的一元二次方程,求a,b的值.小明是这样考虑的:满足条件的a,b必须满足
或
解得
你觉得小明的这种想法全面吗?请你给出另外满足的条件,并求出满足条件的a,b的值.
或
小试牛刀
【思路点拨】x的指数可以为0,1,2这三种情况,应对其指数的不同情况进行分类讨论.
解:不全面,还有
或
或
解得
或
或
解得或或故满足条件的a,b的值可以为① ,- ;②1,0;③ , ;④1,-1;⑤ ,- .
课堂小结
课堂小结
判别一元二次方程的“两方法”:
(1)根据定义要把握三点:一是整式方程;二是含有一个未知数;三是未知数的最高次数是2.
(2)根据一般形式要把握两点:一是能化成ax2+bx+c=0的形式,且a一定不能为0,而b,c都可以为0;二是判断是否为一元二次方程与其解的情况无关.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
2.1 认识一元二次方程
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
幼儿园某教室矩形地面的长为8 m,宽为5 m,现准备在地面正中间铺设一块面积为18 m2的地毯,四周未铺地毯的条形区域的宽度都相同,你能求出这个宽度吗?
如果设所求的宽度为x m,
那么你能列出怎样的方程?
观察下面等式:
102+112+122=132+142.
情景导入
你还能找到五个连续整数,使前三个数的平方和等于后两个数的平方和吗?
如果将这五个连续整数中的第一个数设为x,那么怎样用含x的代数式表示其余四个数?根据题意,你能列出怎样的方程?
情景导入
如图,一个长为10 m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8 m.如果梯子的顶端下滑1 m,那么梯子的底端滑动多少米?
你能计算出滑动前梯子底端距墙的距离吗?如果设梯子底端滑动x m,那么你能列出怎样的方程?
新课精讲
探索新知
1
知识点
一元二次方程的定义
议一议
由上面三个问题,我们可以得到三个方程:
(8-2x)(5-2x)=18,
x2+(x+1)2+(x+2)2=(x+3)2+(x+4)2,
(x+6)2+72=102.
这三个方程有什么共同特点?
探索新知
1.定义:只含有一个未知数x的整式方程,并且都可以化成ax2+bx+c=0(a,b,c为常数,a≠0)的形式,这样的方程叫做一元二次方程.
2.一元二次方程的识别方法:整理前是整式方程,且只含一个未知数;整理后未知数的最高次数是2.
探索新知
例1 下列方程:①x2+y-6=0;②x2+ =2;
③x2-x-2=0;④x2-2+5x3-6x=0;
⑤2x2-3x=2(x2-2),是一元二次方程的有( )
A.1个 B. 2个 C.3个 D.4个
A
导引:要判断一个方程是否是一元二次方程,要从原方程及整理后的方程两方面进行判断,看其是否符合一元二次方程的条件.①中有两个未知数;②不是整式方程;④未知数的最高次数是3;⑤整理后二次项系数为零.
探索新知
总 结
一元二次方程的识别方法:
整理前:①整式方程,②只含一个未知数;
整理后:未知数的最高次数是2.
典题精讲
下列关于x的方程一定是一元二次方程的是( )
A.ax2+bx+c=0 B.x2+1-x2=0
C.x2+ =2 D.x2-x-2=0
若方程(m-1)x|m|+1-2x=3是关于x一元二次方程,则( )
A.m=1 B. m=-1
C. m=±1 D.m≠±1
1
2
D
B
探索新知
2
知识点
一元二次方程的一般形式
一般地,任何一个关于x的一元二次方程,经过整理,都能化成如下形式:ax +bx+c=0 (a≠0)这种形式叫做一元二次方程的一般形式 .
探索新知
一元二次方程的项和各项系数
a x +b x+ c =0
二次项系数
一次项系数
a≠0
二次项
一次项
常数项
探索新知
例2 将方程3x(x-1)=5(x+2)化成一元二次方程的一般形式,并写出其中的二次项系数、一次项系数和常数项.
去括号,得3x2-3x=5x+10.
移项,合并同类项,得一元二次方程的一般形式
3x2-8x-10=0.
其中二次项系数为3,一次项系数为-8,常数项为-10.
解:
探索新知
总 结
(1)ax2+bx+c=0,当a≠0时,方程才是一元二次方程,但b,c可以是0.
(2)将一个一元二次方程化成一般形式,可以通过去分母、去括号、移项、合并同类项等步骤.
(3)指出一元二次方程的某项时,应连同未知数一起;指出某项系数时应连同它前面的符号一起.
典题精讲
把方程x(x+2)=5(x-2)化成一般形式,则a,b,c的值分别是( )
A.1,-3,10 B.1,7,-10
C.1,-5,12 D.1,3,2
A
关于x的一元二次方程(m-1)x2+5x+|m|-1=0的常数项为0,则m等于( )
A.1 B.-1
C.1或-1 D.0
B
探索新知
3
知识点
建立一元二次方程的模型
一元二次方程模型:一元二次方程是刻画现实世 界的一个有效数学模型,它是把实际问题中语言叙述的数量关系通过设未知数用一元二次方程来表达.
常用一元二次方程来建模的问题有:图形的面积、增长(利润)率、行程问题、工程问题等.
探索新知
例3 小雨在一幅长90 cm,宽40 cm的油画四周外围镶上一条宽度相同的边框,制成一幅挂图并使油画画面的面积是整个挂图面积 的54%,设边框的宽度为x cm,根据题意,列出方程.
本题涉及两个基本量:油画的面积与整个挂图的面积.
在油画四周外围镶上宽度为x cm的边框,则整个挂图的长与宽各增加了多少?
利用长方形的面积公式和油画面积与整个挂图面积之间的关系列方程
x
90
40
40+2x
90+2x
解:(90+2x)(40+2x)×54%=90×40.
探索新知
总 结
建立一元二次方程模型解决实际问题时,既要根据题目条件中给出的等量关系,又要抓住题目中隐含的一些常用关系式(如面积公式、体积公式、利润公式等)进行列方程.
典题精讲
随州市 “桃花节”观赏人数逐年增加,据有关部门统计,2014年约为20万人次,2016年约为28.8万人次,设观赏人数年均增长率为x,则下列方程中正确的是( )
A.20(1+2x)=28.8
B.28.8(1+x)2=20
C.20(1+x2)=28.8
D. 20+(1+2x)+20(1+x)2=28.8
C
学以致用
小试牛刀
1.等号两边都是整式,只含有____个未知数,并且未知数的最高次数是____的方程,叫做一元二次方程.它具备三个特征:
(1)等式两边都是整式;
(2)只含____个未知数;
(3)未知数的最高次数是____.
一
2
一
2
2.一元二次方程x2-2x=1的一般形式是___________________,二次项系数是___,一次项系数是____,常数项是____.
x2-2x-1=0
1
-2
-1
小试牛刀
3.把一元二次方程(x+1)(1-x)=2x化成二次项系数大于0的一般形式是_________________.
x2+2x-1=0
4.在某次集会中,参加集会的每两人都握了一次手,一共握了66次手,有多少人参加了这次集会?
解:设有x人参加了这次集会,则每人握了_________次手,由于每两人只握一次手,因此总共握了____________次手,列方程得________________________,化成一般形式为_____________________.
(x-1)
x(x-1)
x(x-1)=66
x2-x-132=0
小试牛刀
5.若关于x的方程(a-2)x2-2ax+a+2=0是一元二次方程,则( )
A.a=2 B.a=-2
C.a=0 D.a≠2
D
6.以下是关于x的一元二次方程的是( )
A.x2- =2 B.ax2+bx+c=0
C.3x2-2xy+y2=0 D.(x- )2=0
D
小试牛刀
7.一元二次方程4x2+x=1的二次项系数 一次项系数 常数项分别是( )
A.4,0,1 B.4,1,1 C.4,1,-1 D.4,1,0
C
8.共享单车为市民出行带来了方便.某单车公司第一个月投放1 000辆单车,计划第三个月投放单车数量比第一个月多440辆.设该公司第二 三两个月投放单车数量的月平均增长率为x,则所列方程正确的为( )
A.1 000(1+x)2=1 000+440 B.1 000(1+x)2=440
C.440(1+x)2=1 000 D.1 000(1+2x)=1 000+440
A
小试牛刀
9.如图,某小区计划在一块长为32 m,宽为20 m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570 m2.若设道路的宽为x m,则下面所列方程正确的是( )
A . (32-x)(20-x)=570
B.32x+2×20x=32×20-570
C.(32-x)(20-x)=32×20-570
D.32x+2×20x-2x2=570
A
小试牛刀
10.已知关于x的方程(m2-1)x2-(m+1)x+m=0.
(1)m为何值时,此方程为一元一次方程?
解:若方程为一元一次方程,
∴m=1.
则有
(2)m为何值时,此方程为一元二次方程?并写出一元二次方程的二次项系数 一次项系数及常数项.
若方程为一元二次方程,
则有m2-1≠0,即m≠±1.
二次项系数:m2-1,一次项系数:-(m+1),常数项:m.
小试牛刀
11.若x2a+b-2xa-b+3=0是关于x的一元二次方程,求a,b的值.小明是这样考虑的:满足条件的a,b必须满足
或
解得
你觉得小明的这种想法全面吗?请你给出另外满足的条件,并求出满足条件的a,b的值.
或
小试牛刀
【思路点拨】x的指数可以为0,1,2这三种情况,应对其指数的不同情况进行分类讨论.
解:不全面,还有
或
或
解得
或
或
解得或或故满足条件的a,b的值可以为① ,- ;②1,0;③ , ;④1,-1;⑤ ,- .
课堂小结
课堂小结
判别一元二次方程的“两方法”:
(1)根据定义要把握三点:一是整式方程;二是含有一个未知数;三是未知数的最高次数是2.
(2)根据一般形式要把握两点:一是能化成ax2+bx+c=0的形式,且a一定不能为0,而b,c都可以为0;二是判断是否为一元二次方程与其解的情况无关.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
