苏教版(新)六上-第一单元 5.表面涂色的正方体【优质课件】
文档属性
| 名称 | 苏教版(新)六上-第一单元 5.表面涂色的正方体【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 11:30:59 | ||
图片预览




文档简介
(共18张PPT)
表面涂色的正方体
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
1
课前导入
2
新课精讲
3
学以致用
4
课堂小结
目 录
课前导入
01
情景导入
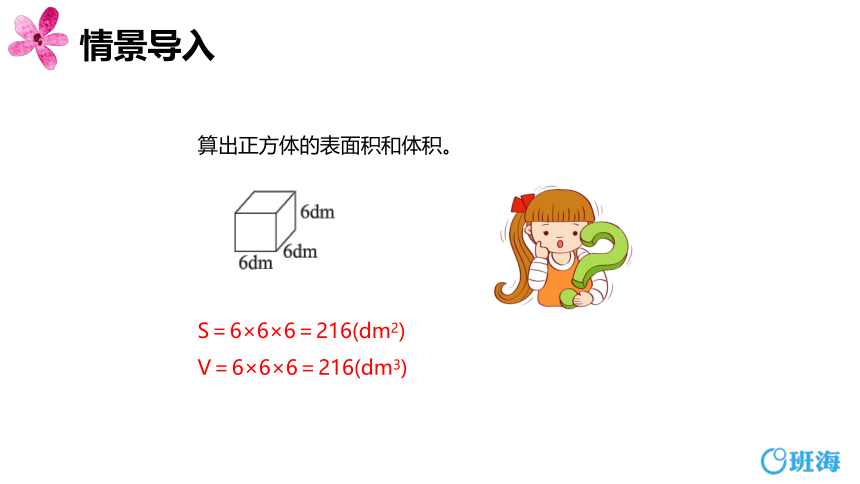
S=6×6×6=216(dm2)
V=6×6×6=216(dm3)
算出正方体的表面积和体积。
新课精讲
02
探索新知
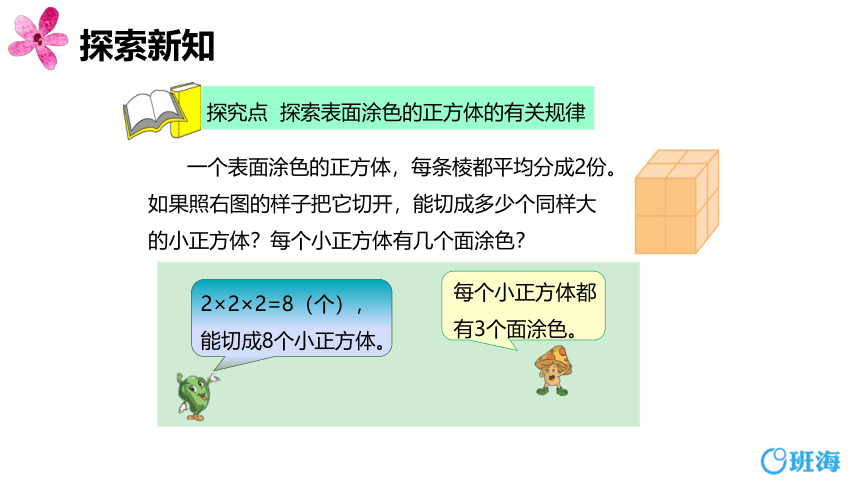
一个表面涂色的正方体,每条棱都平均分成2份。如果照右图的样子把它切开,能切成多少个同样大的小正方体?每个小正方体有几个面涂色?
2×2×2=8(个),
能切成8个小正方体。
每个小正方体都有3个面涂色。
探究点 探索表面涂色的正方体的有关规律
探索新知
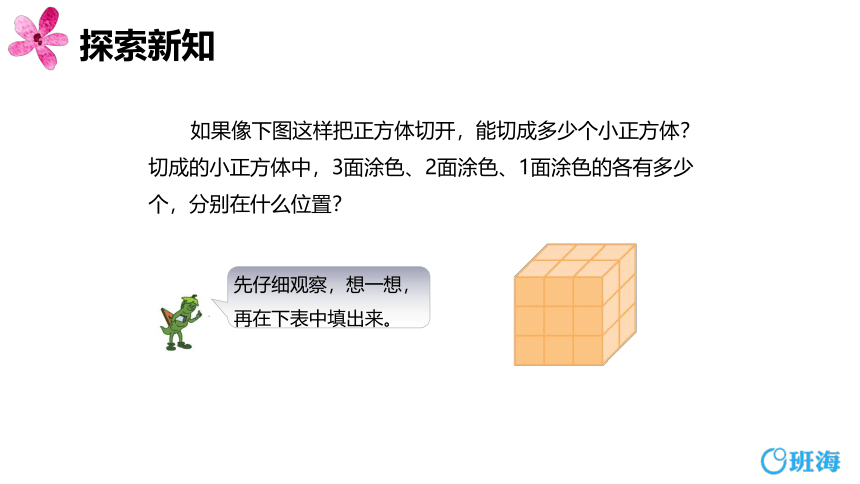
如果像下图这样把正方体切开,能切成多少个小正方体?切成的小正方体中,3面涂色、2面涂色、1面涂色的各有多少个,分别在什么位置?
先仔细观察,想一想,再在下表中填出来。
探索新知
如果把这个正方体的每条棱平均分成4份、5份……再切成同样大的小正方体,结果会怎样?先在图中找一找,再把结果填入下表,与同学交流。
大正方体的棱平均分的份数 2 3 4 5 …
切成小正方体的总个数
3面涂色的小正方体个数
2面涂色的小正方体个数
1面涂色的小正方体个数
8
8
8
8
8
27
64
125
0
0
12
24
36
6
24
54
探索新知
(n-2)×12
观察填出的表格,你能发现什么规律?
3面涂色的小正方体都在大正方体顶点的位置,都是8个。
2面涂色的小正方体
的个数都是12的倍数。
1面涂色的小正方体
的个数都是6的倍数。
如果用n表示大正方体的棱平均分的份数,用a、b分别表示2面涂色和1面涂色的小正方体个数,你能用式子分别表示n和a、b的关系吗?
a =
b=
(n-2)2×6
探索新知
回顾探索和发现规律的过程,说说你的体会。
找各种小正方体时,
要注意它们在大正方体上的位置。
各种小正方体的个数与正方体顶点、面和棱的个(条)数有关。
要把找、数、算等方
法结合起来,并根据
图形的特征进行思考。
典题精讲
1.把一个棱长为4厘米的正方体表面涂色,然后切成棱长为1厘米的小正方体,6面都没涂色的小正方体有多少个
8个
2.把若干个相同的小正方体堆成一个大正方体,然后在表面涂上颜色,如果2面涂色的小正方体有60个,那么1面涂色的小正方体有多少个?这些小正方体一共有多少个?
1面涂色的小正方体有150个,这些小正方体一共有343个。
学以致用
03
小试牛刀
1.如图是用体积为1 cm3的小正方体拼成的大正方体,一共用了( )个。在这个大正方体的表面涂色,小正方体三面涂色的在大正方体的( )位置,有( )个,两面涂色的在大正方体的( )上,有( )个,一面涂色的在大正方体( )的位置,有( )个,没有涂色的有( )个。
27
顶点
8
棱
12
每个面中间
6
1
小试牛刀
2.如果用n表示表面涂色的大正方体每条棱被平均分成的段数,用a、b、c分别表示2面涂色,1面涂色和6个面都不涂色的小正方体个数,那么a=( ),b=( ),c=( )。(用含有n的式子表示)
6(n-2)2
12(n-2)
(n-2)3
小试牛刀
3.一个棱长1分米的正方体木块,表面涂满了红色,把它切成棱长1厘米的小正方体。在这些小正方体中:
(1)三个面涂色的有多少个?
(2)两个面涂色的有多少个?
(3)一个面涂色的有多少个?
(4)六个面都没有涂色的有多少个?
8个
96个
384个
512个
课堂小结
04
归纳总结:
一个表面涂色的正方体,把每条棱平均分成相等的若干份,然后切成同样大的小正方体。
(1)3面涂色的小正方体有8个;
(2)如果用n表示把正方体的棱平均分成的份数(n大于或等于2的自然数),用a、b分别表示2面涂色和1面涂色的小正方体的个数,那么a=(n-2)2×12,b=(n-2)2×6。
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
表面涂色的正方体
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
1
课前导入
2
新课精讲
3
学以致用
4
课堂小结
目 录
课前导入
01
情景导入
S=6×6×6=216(dm2)
V=6×6×6=216(dm3)
算出正方体的表面积和体积。
新课精讲
02
探索新知
一个表面涂色的正方体,每条棱都平均分成2份。如果照右图的样子把它切开,能切成多少个同样大的小正方体?每个小正方体有几个面涂色?
2×2×2=8(个),
能切成8个小正方体。
每个小正方体都有3个面涂色。
探究点 探索表面涂色的正方体的有关规律
探索新知
如果像下图这样把正方体切开,能切成多少个小正方体?切成的小正方体中,3面涂色、2面涂色、1面涂色的各有多少个,分别在什么位置?
先仔细观察,想一想,再在下表中填出来。
探索新知
如果把这个正方体的每条棱平均分成4份、5份……再切成同样大的小正方体,结果会怎样?先在图中找一找,再把结果填入下表,与同学交流。
大正方体的棱平均分的份数 2 3 4 5 …
切成小正方体的总个数
3面涂色的小正方体个数
2面涂色的小正方体个数
1面涂色的小正方体个数
8
8
8
8
8
27
64
125
0
0
12
24
36
6
24
54
探索新知
(n-2)×12
观察填出的表格,你能发现什么规律?
3面涂色的小正方体都在大正方体顶点的位置,都是8个。
2面涂色的小正方体
的个数都是12的倍数。
1面涂色的小正方体
的个数都是6的倍数。
如果用n表示大正方体的棱平均分的份数,用a、b分别表示2面涂色和1面涂色的小正方体个数,你能用式子分别表示n和a、b的关系吗?
a =
b=
(n-2)2×6
探索新知
回顾探索和发现规律的过程,说说你的体会。
找各种小正方体时,
要注意它们在大正方体上的位置。
各种小正方体的个数与正方体顶点、面和棱的个(条)数有关。
要把找、数、算等方
法结合起来,并根据
图形的特征进行思考。
典题精讲
1.把一个棱长为4厘米的正方体表面涂色,然后切成棱长为1厘米的小正方体,6面都没涂色的小正方体有多少个
8个
2.把若干个相同的小正方体堆成一个大正方体,然后在表面涂上颜色,如果2面涂色的小正方体有60个,那么1面涂色的小正方体有多少个?这些小正方体一共有多少个?
1面涂色的小正方体有150个,这些小正方体一共有343个。
学以致用
03
小试牛刀
1.如图是用体积为1 cm3的小正方体拼成的大正方体,一共用了( )个。在这个大正方体的表面涂色,小正方体三面涂色的在大正方体的( )位置,有( )个,两面涂色的在大正方体的( )上,有( )个,一面涂色的在大正方体( )的位置,有( )个,没有涂色的有( )个。
27
顶点
8
棱
12
每个面中间
6
1
小试牛刀
2.如果用n表示表面涂色的大正方体每条棱被平均分成的段数,用a、b、c分别表示2面涂色,1面涂色和6个面都不涂色的小正方体个数,那么a=( ),b=( ),c=( )。(用含有n的式子表示)
6(n-2)2
12(n-2)
(n-2)3
小试牛刀
3.一个棱长1分米的正方体木块,表面涂满了红色,把它切成棱长1厘米的小正方体。在这些小正方体中:
(1)三个面涂色的有多少个?
(2)两个面涂色的有多少个?
(3)一个面涂色的有多少个?
(4)六个面都没有涂色的有多少个?
8个
96个
384个
512个
课堂小结
04
归纳总结:
一个表面涂色的正方体,把每条棱平均分成相等的若干份,然后切成同样大的小正方体。
(1)3面涂色的小正方体有8个;
(2)如果用n表示把正方体的棱平均分成的份数(n大于或等于2的自然数),用a、b分别表示2面涂色和1面涂色的小正方体的个数,那么a=(n-2)2×12,b=(n-2)2×6。
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
