北师大版(新)七上-1.4 从三个方向看物体的形状【优质课件】
文档属性
| 名称 | 北师大版(新)七上-1.4 从三个方向看物体的形状【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览









文档简介
(共37张PPT)
1.4 从三个方向看物体的形状
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
题 西 林 壁
---苏轼
横看成岭侧成峰,远近高低各不同.
不识庐山真面目,只缘身在此山中.
新课精讲
探索新知
1
知识点
从不同方向看简单立体图形
“横看成岭侧成峰”一句中,蕴含了怎样的数学道理
对于一些立体图形的问题,常把它们转化为平面图形来研究和处理.从不同方向看立体图形,往往会得到不同形状的平面图形.在建筑、工程等设计中,也常常用从不同方向看到的平面图形来表示立体图形.
这是一个工件的立体图,设计师们常常画出从不同方向看它得到
的平面图形来表示它.
探索新知
探索新知
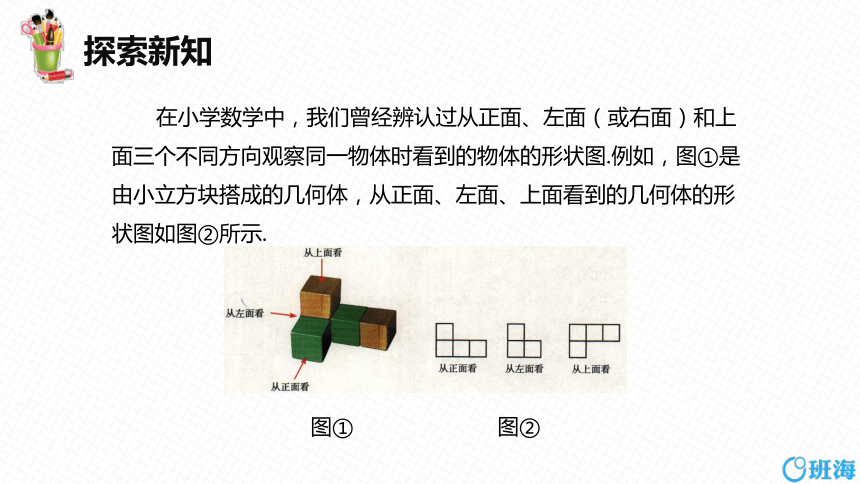
在小学数学中,我们曾经辨认过从正面、左面(或右面)和上面三个不同方向观察同一物体时看到的物体的形状图.例如,图①是由小立方块搭成的几何体,从正面、左面、上面看到的几何体的形状图如图②所示.
图①
图②
探索新知
1.我们从三个不同方向观察同一物体时,一般可以看到不同的形状.从正面能够看到物体的长和高,从上面能够看到物体的长和宽,从左面能够看到物体的宽和高.
2.易错警示:画从三个不同方向看一个立体图形所得的形状图时,要注意进行水平观察,且要分清物体的前后位置.
探索新知
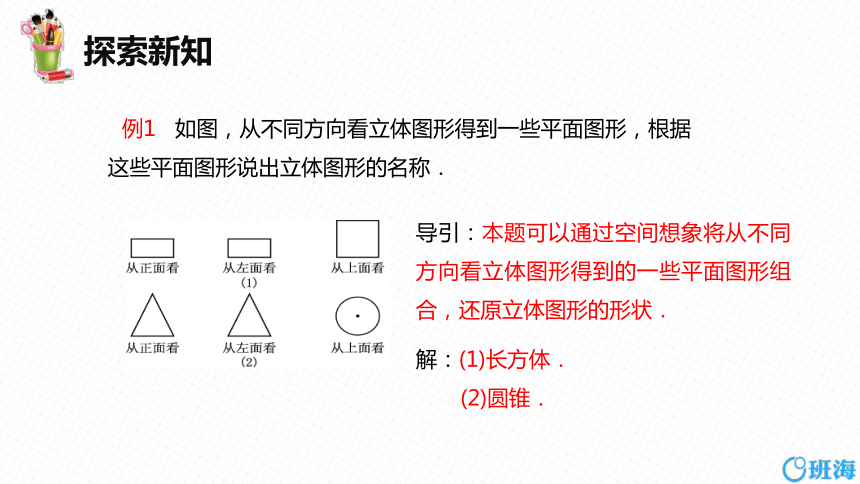
例1 如图,从不同方向看立体图形得到一些平面图形,根据这些平面图形说出立体图形的名称.
导引:本题可以通过空间想象将从不同方向看立体图形得到的一些平面图形组合,还原立体图形的形状.
解:(1)长方体.
(2)圆锥.
探索新知
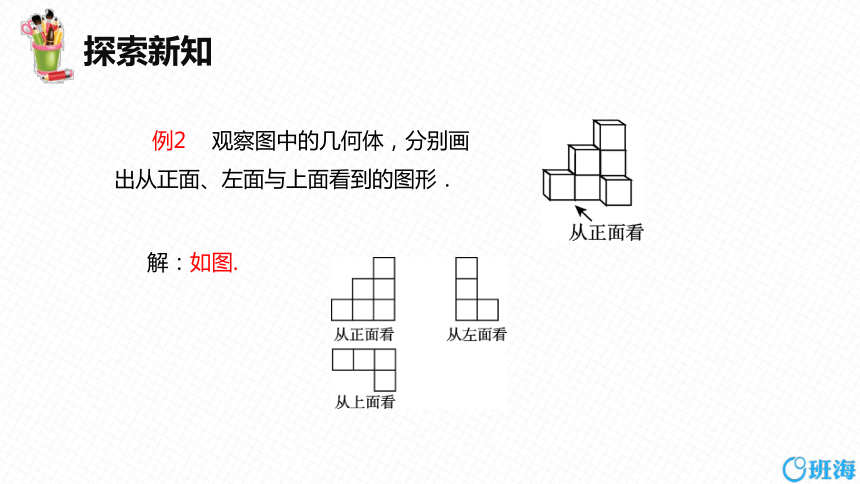
解:如图.
例2 观察图中的几何体,分别画出从正面、左面与上面看到的图形.
探索新知
总 结
本题可运用动手操作法,这也是解决这类问题
的有效途径.画图时要注意:画从正面看的图与从
上面看的图要“长对正”,即长相等;画从正面看
的图与从左面看的图要“高平齐”,即高相等;画
从左面看的图与从上面看的图要“宽相等”.
典题精讲
下列立体图形中,从上面看是正方形的是( )
下列几何体中,从正面看和从左面看都是长方形的是( )
B
B
典题精讲
下面四个几何体中,从上面看得到的形状图是圆的几何体共有( )
A.1个 B.2个 C.3个 D.4个
B
典题精讲
4 如图,是由一个圆柱体和一个长方体组成的几何体.其从正面看到的形状图是( )
B
典题精讲
5 桌面上放着一个长方体和一个圆柱体,按如图所示的方式摆放在一起,从左面看得到的形状图是( )
C
探索新知
2
知识点
根据从不同方向看到的形状图还原物体
议一议
一个几何体由几个大小
相同的小立方块搭成,
从上面和从左面看到的这个几何体的形状图如图所示,请搭出满足条件的几何体.你搭的几何体由几个小立方块构成?与同伴进行交流.
探索新知
画从正面和左面看到的形状图,有两种方法:
方法一是先根据从上面看到的形状图摆出几何体,再画从正面和左面看到的形状图;方法二是先根据从上面看到的形状图确定从正面和左面看到的图形的列数,再确定每列正方形的个数.我们通常采用第二种方法.
探索新知
例3 如图是从上面看到的由几个小立方块所搭
成的几何体的形状图,小正方形中的数字
表示在该位置的小立方块的个数,请画出
从正面和左面看这个几何体的形状图.
导引:先根据从上面看到的几何体的形状图来确定从正面和左面看到的列数,再根据小正方形中的数字确定每列小正方形的个数,从而画出图形.
解:如图.
典题精讲
例4 如图,是从正面、左面、上面看到的由一些大小相同的小立方块搭成的几何体的形状图,那么搭成这个几何体的小立方块的
个数是( )
A.6 B.7 C.8 D.9
B
探索新知
总 结
根据从正面看到的形状图和从左面看到的形状图在从上面看到的几何体的形状图中标上数字,然后求和即可.
典题精讲
一个几何体从三个方向看得到的形状图如图所示,则这个几何体是( )
A.三棱锥 B.三棱柱
C.圆柱 D.长方体
B
学以致用
小试牛刀
1.对于一些立体图形的问题,常把它们转化为________图形来研究和处理.从不同的方向看,将会得到不同形状的平面图形.通常我们是从________、________、 三个方向看,从而得到相应的平面图形.
平面
正面
左面
2.下列立体图形中,从正面看是圆的是( )
A
上面
小试牛刀
3.如图所示的几何体,从上面看到的图形为( )
D
小试牛刀
4.如图,小明、小东、小刚和小华四人坐在桌子周围,桌子正中央有一把水壶,请选择他们分别看到的是水壶的哪个面:
小明:______,小东:______,小刚:______,小华:______.
D
C
B
A
小试牛刀
5.一个几何体从三个方向看到的平面图形如图所示,这个几何体是( )
A.球 B.圆柱 C.圆锥 D.立方体
B
小试牛刀
6.已知:如图,是由若干个大小相同的小正方体所搭成的几何体从三个方向看到的平面图形,则搭成这个几何体的小正方体的个数是( )
A.6 B.7 C.8 D.9
B
小试牛刀
7.如图是由5块完全相同的小正方体所搭成的立体图形从上面看到的图形,小正方形中的数字表示在该位置小正方体的个数,其从正面看到的图形是( )
B
小试牛刀
8.找出与图中几何体对应的从三个方向看到的图形,并在横线上填上对应的序号.
③
①
④
②
小试牛刀
9.5个棱长为1的正方体组成如图所示的几何体.
(1)该几何体的体积是________(立方单位),表面积是________(平方单位);
5
22
(2)画出该几何体从正面、左面、上面看到的图形.
解:如图所示.
小试牛刀
10.如图是一个几何体从正面和上面看到的图形,求这个几何体的体积(π取3.14).
解:这个几何体的体积为30×25×40+3.14× ×32=30 000+10 048=40 048(cm3).
小试牛刀
11.学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与高度(单位:cm)的关系如下表:
碟子的个数 碟子的高度
1 2
2 2+1.5
3 2+3
4 2+4.5
… …
小试牛刀
(1)当桌子上放有x个碟子时,请写出此时碟子的高度(用含x的式子表示);
解:碟子的高度为(1.5x+0.5)cm.
(2)分别从三个方向看若干碟子,得到的图形如图所示,厨房师傅想把它们整齐地叠成一摞,求叠成一摞后的高度.
解:由题图知共有3摞碟子,摆放情况如图(数字表示在该位置的碟子的个数):
所以共有4+5+3=12(个)碟子.
1.5×12+0.5=18.5(cm),
所以叠成一摞后的高度为18.5 cm.
课堂小结
课堂小结
从不同的方向看立体图形的技巧:
(1)从正面看立体图形时,可以想象为:将几何体从前
向后压缩,使看到的面全部落在同一竖直的平面内.
(2)从左面看立体图形时,可以想象为:将几何体从左
向右压缩,使看到的面全部落在同一竖直的平面内.
(3)从上面看立体图形时,可以想象为:将几何体从上
向下压缩,使看到的面全部落在同一水平的平面内.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
1.4 从三个方向看物体的形状
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
题 西 林 壁
---苏轼
横看成岭侧成峰,远近高低各不同.
不识庐山真面目,只缘身在此山中.
新课精讲
探索新知
1
知识点
从不同方向看简单立体图形
“横看成岭侧成峰”一句中,蕴含了怎样的数学道理
对于一些立体图形的问题,常把它们转化为平面图形来研究和处理.从不同方向看立体图形,往往会得到不同形状的平面图形.在建筑、工程等设计中,也常常用从不同方向看到的平面图形来表示立体图形.
这是一个工件的立体图,设计师们常常画出从不同方向看它得到
的平面图形来表示它.
探索新知
探索新知
在小学数学中,我们曾经辨认过从正面、左面(或右面)和上面三个不同方向观察同一物体时看到的物体的形状图.例如,图①是由小立方块搭成的几何体,从正面、左面、上面看到的几何体的形状图如图②所示.
图①
图②
探索新知
1.我们从三个不同方向观察同一物体时,一般可以看到不同的形状.从正面能够看到物体的长和高,从上面能够看到物体的长和宽,从左面能够看到物体的宽和高.
2.易错警示:画从三个不同方向看一个立体图形所得的形状图时,要注意进行水平观察,且要分清物体的前后位置.
探索新知
例1 如图,从不同方向看立体图形得到一些平面图形,根据这些平面图形说出立体图形的名称.
导引:本题可以通过空间想象将从不同方向看立体图形得到的一些平面图形组合,还原立体图形的形状.
解:(1)长方体.
(2)圆锥.
探索新知
解:如图.
例2 观察图中的几何体,分别画出从正面、左面与上面看到的图形.
探索新知
总 结
本题可运用动手操作法,这也是解决这类问题
的有效途径.画图时要注意:画从正面看的图与从
上面看的图要“长对正”,即长相等;画从正面看
的图与从左面看的图要“高平齐”,即高相等;画
从左面看的图与从上面看的图要“宽相等”.
典题精讲
下列立体图形中,从上面看是正方形的是( )
下列几何体中,从正面看和从左面看都是长方形的是( )
B
B
典题精讲
下面四个几何体中,从上面看得到的形状图是圆的几何体共有( )
A.1个 B.2个 C.3个 D.4个
B
典题精讲
4 如图,是由一个圆柱体和一个长方体组成的几何体.其从正面看到的形状图是( )
B
典题精讲
5 桌面上放着一个长方体和一个圆柱体,按如图所示的方式摆放在一起,从左面看得到的形状图是( )
C
探索新知
2
知识点
根据从不同方向看到的形状图还原物体
议一议
一个几何体由几个大小
相同的小立方块搭成,
从上面和从左面看到的这个几何体的形状图如图所示,请搭出满足条件的几何体.你搭的几何体由几个小立方块构成?与同伴进行交流.
探索新知
画从正面和左面看到的形状图,有两种方法:
方法一是先根据从上面看到的形状图摆出几何体,再画从正面和左面看到的形状图;方法二是先根据从上面看到的形状图确定从正面和左面看到的图形的列数,再确定每列正方形的个数.我们通常采用第二种方法.
探索新知
例3 如图是从上面看到的由几个小立方块所搭
成的几何体的形状图,小正方形中的数字
表示在该位置的小立方块的个数,请画出
从正面和左面看这个几何体的形状图.
导引:先根据从上面看到的几何体的形状图来确定从正面和左面看到的列数,再根据小正方形中的数字确定每列小正方形的个数,从而画出图形.
解:如图.
典题精讲
例4 如图,是从正面、左面、上面看到的由一些大小相同的小立方块搭成的几何体的形状图,那么搭成这个几何体的小立方块的
个数是( )
A.6 B.7 C.8 D.9
B
探索新知
总 结
根据从正面看到的形状图和从左面看到的形状图在从上面看到的几何体的形状图中标上数字,然后求和即可.
典题精讲
一个几何体从三个方向看得到的形状图如图所示,则这个几何体是( )
A.三棱锥 B.三棱柱
C.圆柱 D.长方体
B
学以致用
小试牛刀
1.对于一些立体图形的问题,常把它们转化为________图形来研究和处理.从不同的方向看,将会得到不同形状的平面图形.通常我们是从________、________、 三个方向看,从而得到相应的平面图形.
平面
正面
左面
2.下列立体图形中,从正面看是圆的是( )
A
上面
小试牛刀
3.如图所示的几何体,从上面看到的图形为( )
D
小试牛刀
4.如图,小明、小东、小刚和小华四人坐在桌子周围,桌子正中央有一把水壶,请选择他们分别看到的是水壶的哪个面:
小明:______,小东:______,小刚:______,小华:______.
D
C
B
A
小试牛刀
5.一个几何体从三个方向看到的平面图形如图所示,这个几何体是( )
A.球 B.圆柱 C.圆锥 D.立方体
B
小试牛刀
6.已知:如图,是由若干个大小相同的小正方体所搭成的几何体从三个方向看到的平面图形,则搭成这个几何体的小正方体的个数是( )
A.6 B.7 C.8 D.9
B
小试牛刀
7.如图是由5块完全相同的小正方体所搭成的立体图形从上面看到的图形,小正方形中的数字表示在该位置小正方体的个数,其从正面看到的图形是( )
B
小试牛刀
8.找出与图中几何体对应的从三个方向看到的图形,并在横线上填上对应的序号.
③
①
④
②
小试牛刀
9.5个棱长为1的正方体组成如图所示的几何体.
(1)该几何体的体积是________(立方单位),表面积是________(平方单位);
5
22
(2)画出该几何体从正面、左面、上面看到的图形.
解:如图所示.
小试牛刀
10.如图是一个几何体从正面和上面看到的图形,求这个几何体的体积(π取3.14).
解:这个几何体的体积为30×25×40+3.14× ×32=30 000+10 048=40 048(cm3).
小试牛刀
11.学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与高度(单位:cm)的关系如下表:
碟子的个数 碟子的高度
1 2
2 2+1.5
3 2+3
4 2+4.5
… …
小试牛刀
(1)当桌子上放有x个碟子时,请写出此时碟子的高度(用含x的式子表示);
解:碟子的高度为(1.5x+0.5)cm.
(2)分别从三个方向看若干碟子,得到的图形如图所示,厨房师傅想把它们整齐地叠成一摞,求叠成一摞后的高度.
解:由题图知共有3摞碟子,摆放情况如图(数字表示在该位置的碟子的个数):
所以共有4+5+3=12(个)碟子.
1.5×12+0.5=18.5(cm),
所以叠成一摞后的高度为18.5 cm.
课堂小结
课堂小结
从不同的方向看立体图形的技巧:
(1)从正面看立体图形时,可以想象为:将几何体从前
向后压缩,使看到的面全部落在同一竖直的平面内.
(2)从左面看立体图形时,可以想象为:将几何体从左
向右压缩,使看到的面全部落在同一竖直的平面内.
(3)从上面看立体图形时,可以想象为:将几何体从上
向下压缩,使看到的面全部落在同一水平的平面内.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
