北师大版(新)七上-2.1有理数【优质课件】
文档属性
| 名称 | 北师大版(新)七上-2.1有理数【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:52:22 | ||
图片预览











文档简介
(共38张PPT)
2.1 有理数
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
某班举行知识竞赛,评分标准是:答对一题加1分,答错一题扣1分,不 回答得0分;每个队的基本分均为0分.两个队答题情况如下表:
答题情况
第一队
第二队
情景导入
如果答对题所得的分数用正数表示,那么你能写出每个队答题得分的情况吗?试完成下表:
答对题的得分 答错题的得分 未回答题的得分
第一队 +6
第二队 -2
新课精讲
探索新知
1
知识点
正数和负数
1.定义:大于0的数叫做正数,在正数前面加上符号“-”(负)的数叫做负数.
要点精析:(1)正数的实质就是大于0的任何数,它可以含“+”,也可以不含“+”;
(2)负数就是在正数前面加上“-”的数,每一个正数都对应一个负数;
(3)判断一个数是正、负数的方法:①不为零;②含“+”“-”的情况 (无“+” “-”视同含“+”),两者必须同时看.
探索新知
2. 数的特征及种类:
(1)数有带符号(+、-)的数和不带符号的数两种呈现形式;
(2)数包括正数、0、负数三种情况.
拓展:符号“+” “-”的含义:
(1)作为运算符号是加减号;
(2)作为数的性质是正负号.
探索新知
例1 下列各数中,哪些是正数?哪些是负数?
+0.005,-100, 0.333…,-4,5,0.
导引:直接根据定义判断即可.
解:正数:+0.005,
负数:-100,
警示:0既不是正数,也不是负数.
探索新知
总 结
解题关键点 特征 结论
看符号 数(0除外)前面带“+” 或无符号 正数
数(0除外)前面带 “-”的数 负数
典题精讲
2 下列各组数,都是正数或都是负数的是( )
A.8,4,-2 B.2,5.4,
C.-6,0.5,0 D.0,6,9
1 四个数-3.14,0,1,2中为负数的是( )
A.-3.14 B.0 C.1 D.2
A
B
探索新知
2
知识点
具有相反意义的量
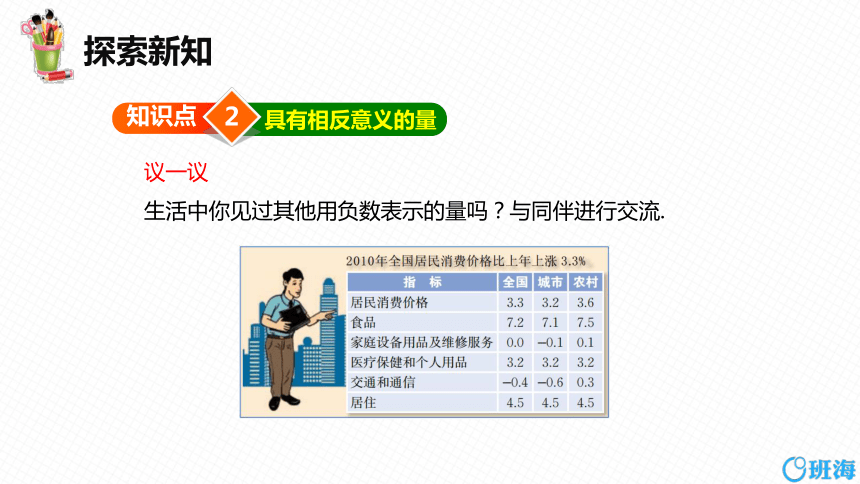
议一议
生活中你见过其他用负数表示的量吗?与同伴进行交流.
探索新知
“加分与扣分” “上涨量与下跌量” “零上温度与零下温度”等都是具有相 反意义的量.为了表示具有相反意义的量,我们可把其中一个量规定为正的,用正数 来表示,而把与这个量意义相反的量规定为负的,用负数来表示.例如,把上涨3.3%记为+3.3%,那么下跌0.6%就记为-0.6%.
探索新知
1.生活中到处都存在相反意义的量.
2.在相反意义的量中,我们把其中一个意义的量规定为正,那么另一个量就是负.
要点精析:
(1)相反意义的量是指意义相反的两个量,相反意义的量是成对出现的.
(2)判断相反意义的量的标准:①两个同类量;②意义相反.
(3)具有相反意义的量的正负性是相对的,且是可以互换的.
探索新知
例2 (1)某人转动转盘,如果用+5圈表示沿逆时针方向转了 5圈,那么沿顺时针方向转了 12圈怎样表示?
(2)在某次乒乓球质量检测中,一只乒乓球超出
标准质量0.02 g记作+0.02 g,
那么- 0.03 g表示什么?
(3)某大米包装袋上标注着“净含
量:10 kg ± 150 g”,这里的
“10 kg ±150 g”表示什么?
探索新知
解:(1)沿顺时针方向转了 12圈记作-12圈;
(2)-0.03 g表示乒乓球的质量低于标准质量0.03 g;
(3)每袋大米的标准质量应为10 kg,但实际每袋大米
可能有150 g的误差,即每袋大米的净含量最多
是10 kg+150 g,最少是10 kg-150 g.
典题精讲
1 如果水位升高6 m时水位变化记作+6m,那么水位下降6 m时水位变化记作( )
A.-3 m B.3 m
C.6 m D.-6 m
D
(来自《典中点》)
2 如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数,从轻重的角度看,最接近标准的是( )
C
探索新知
3
知识点
有理数及其分类
1.定义:整数和分数统称有理数.
要点精析:
(1)一个有理数不是整数就是分数.
(2)如果一个数既不是整数也不是分数,那么它一定不是有理数.
探索新知
2. 整数和分数:正整数、0、负整数统称为整数.
正分数、负分数统称为分数.
要点精析:几种常用整数和分数名词的含义:
(1)正整数:既是正数,又是整数的数;
(2)负整数:既是负数,又是整数的数;
(3)正分数:既是正数,又是分数的数;
(4)负分数:既是负数,又是分数的数;
(5)非负整数:正整数和0;
(6)非正整数:0和负整数.
探索新知
3.有理数的分类:
(1)按定义分类:
有理数
整数
分数
正整数
0
负整数
正分数
负分数
探索新知
(2)按性质分类:
拓展:非负整数包括正整数和0;非正整数包括负整数和0.
要点精析:在进行有理数分类时,要严格按照
同一分类标准,做到不重复不遗漏.
有理数
正有理数
负有理数
正整数
0
正分数
负整数
负分数
探索新知
例3 〈易错题〉 把下列各数分别填入相应的集合
里:-2,0,-0.314,25%,11,
非负有理数集合:{ …};
整数集合:{ …};
自然数集合:{ …};
分数集合:{ …};
非正整数集合:{ …}.
探索新知
导引:要严格按照各类数的概念进行填写,非负有理数包含正有理数和0;非正整数包含负整数和0.
典题精讲
将下列各数填入如图所示的相应的圈内.
正数集合 整数集合 负数集合
学以致用
小试牛刀
1.大于______的数叫做正数;正数是通过与________比较大小来定义的.在正数前面加上符号“-”(负)的数叫做________.负数是相对于________来定义的,只有在正数前面加上______号,所得的数才是负数;在0或负数前面加上负号,所得的数不是负数.
0
0
负数
正数
负
2.相反意义的量必须包含两层含义:第一是具有相反意义;第二是具有一定的量,但不要求数量一定相等.
例:温度上升8 ℃和温度下降5 ℃,具有相反意义的量是:____________和____________.我们可用________和________分别表示在同一问题中出现的具有相反意义的量.
上升8 ℃
正数
下降5 ℃
负数
小试牛刀
3.__________、__________、________统称为整数,________和________统称为分数,________和________统称为有理数.
负整数
负分数
整数
分数
正整数
0
正分数
4.定义:A={b,c,a},B={c},A∪B={a,b,c}.若M={-1},N={0,1,-1},则M∪N={____________}.
-1,0,1
小试牛刀
5.在-3,1.5, , ,-7,0, 中,负数一共有( )
A.1个 B.2个 C.3个 D.4个
6.下列各数中比1大的数是( )
A.2 B.0 C.-1 D.-3
A
C
7.如果向北走6步记作+6步,那么向南走8步记作( )
A.+8步 B.-8步
C.+14步 D.-2步
B
小试牛刀
8.《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是:今有两数若其意义相反,则分别叫做正数与负数.若气温为零上10 ℃记作+10 ℃,则-3 ℃表示气温为( )
A.零上3 ℃ B.零下3 ℃
C.零上7 ℃ D.零下7 ℃
B
小试牛刀
9.下列说法不正确的是( )
A.π既是正数、分数,也是有理数
B.0既不是正数,也不是负数,但是整数
C.-100既是负数,也是整数,同时是有理数
D.0既是非负数,也是非正数
A
小试牛刀
10.把下列各数填入相应的大括号里:
,0.618,-3.14,26,-2, ,0,70%,-π.
正分数:{ …};
整数:{ …};
非负数:{ …};
26,-2,0
0.618, ,70%
0.618 ,26, ,0,70%
负数:{ …};
负有理数:{ …};
有理数:{ …}.
-13,-3.14,-2,-π
-13,-3.14,-2
-13,0.618,-3.14,26,-2, ,0,70%
小试牛刀
11.指出下列各题中正负数表示的意义:
(1)水面上升-8 m;
(2)一个玻璃杯口的直径比标准尺寸大-0.01 mm;
(3)在电视上看到的天气预报,武汉某天的气温为-3 ℃~8 ℃.
解:(2)一个玻璃杯口的直径比标准尺寸小0.01 mm;
解:(1)水面下降8 m;
解:(3)武汉某天的气温在零下3 ℃与8 ℃之间.
小试牛刀
12.有一次同学聚会,小王的座位号与下列一组数中的负数的个数相等,小李的座位号与下列一组数中正整数的个数相等.
数:5, ,0,-100, ,-4.11,-0.01,53, ,-10%,+200,-20.
(1)问小王、小李的座位号各是多少?
(2)若这次同学聚会的人数是小王座位号的2倍与小李座位号的4的和,问这次聚会到了多少名同学?
解:(1)小王的座位号是7,小李的座位号是3.
解:(2)2×7+4×3=14+12=26(名).
答:这次聚会到了26名同学.
小试牛刀
13.将一串有理数按如图所示规律排列,回答下列问题:
(1)在A位置的数是正数还是负数?
解:在A位置的数是正数.
(2)A,B,C,D中哪些位置的数是负数?
(3)第2 018个数是正数还是负数?排在对应于A,B,C,D中的哪个位置?
解:(2)18 (2)B和D位置的数是负数.
解:(3)第2 018个数是正数,排在对应于C的位置.
小试牛刀
【思路点拨】要分析以下3个规律:
(1)上方的数A,B的符号与箭头指向的规律;
(2)偶数为正,奇数为负;
(3)A,B,C,D对应数的规律.
课堂小结
课堂小结
判断具有相反意义的量的方法:
(1)成对出现:具有相反意义的量是成对出现的,且必须是同类量.
(2)单位一致:两个具有相反意义的量在数量上可以不相等,但单位必须一致.
注意:用正数、负数表示相反意义的量时,哪种意
义为正没有硬性规定,并不是一成不变的.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
2.1 有理数
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
某班举行知识竞赛,评分标准是:答对一题加1分,答错一题扣1分,不 回答得0分;每个队的基本分均为0分.两个队答题情况如下表:
答题情况
第一队
第二队
情景导入
如果答对题所得的分数用正数表示,那么你能写出每个队答题得分的情况吗?试完成下表:
答对题的得分 答错题的得分 未回答题的得分
第一队 +6
第二队 -2
新课精讲
探索新知
1
知识点
正数和负数
1.定义:大于0的数叫做正数,在正数前面加上符号“-”(负)的数叫做负数.
要点精析:(1)正数的实质就是大于0的任何数,它可以含“+”,也可以不含“+”;
(2)负数就是在正数前面加上“-”的数,每一个正数都对应一个负数;
(3)判断一个数是正、负数的方法:①不为零;②含“+”“-”的情况 (无“+” “-”视同含“+”),两者必须同时看.
探索新知
2. 数的特征及种类:
(1)数有带符号(+、-)的数和不带符号的数两种呈现形式;
(2)数包括正数、0、负数三种情况.
拓展:符号“+” “-”的含义:
(1)作为运算符号是加减号;
(2)作为数的性质是正负号.
探索新知
例1 下列各数中,哪些是正数?哪些是负数?
+0.005,-100, 0.333…,-4,5,0.
导引:直接根据定义判断即可.
解:正数:+0.005,
负数:-100,
警示:0既不是正数,也不是负数.
探索新知
总 结
解题关键点 特征 结论
看符号 数(0除外)前面带“+” 或无符号 正数
数(0除外)前面带 “-”的数 负数
典题精讲
2 下列各组数,都是正数或都是负数的是( )
A.8,4,-2 B.2,5.4,
C.-6,0.5,0 D.0,6,9
1 四个数-3.14,0,1,2中为负数的是( )
A.-3.14 B.0 C.1 D.2
A
B
探索新知
2
知识点
具有相反意义的量
议一议
生活中你见过其他用负数表示的量吗?与同伴进行交流.
探索新知
“加分与扣分” “上涨量与下跌量” “零上温度与零下温度”等都是具有相 反意义的量.为了表示具有相反意义的量,我们可把其中一个量规定为正的,用正数 来表示,而把与这个量意义相反的量规定为负的,用负数来表示.例如,把上涨3.3%记为+3.3%,那么下跌0.6%就记为-0.6%.
探索新知
1.生活中到处都存在相反意义的量.
2.在相反意义的量中,我们把其中一个意义的量规定为正,那么另一个量就是负.
要点精析:
(1)相反意义的量是指意义相反的两个量,相反意义的量是成对出现的.
(2)判断相反意义的量的标准:①两个同类量;②意义相反.
(3)具有相反意义的量的正负性是相对的,且是可以互换的.
探索新知
例2 (1)某人转动转盘,如果用+5圈表示沿逆时针方向转了 5圈,那么沿顺时针方向转了 12圈怎样表示?
(2)在某次乒乓球质量检测中,一只乒乓球超出
标准质量0.02 g记作+0.02 g,
那么- 0.03 g表示什么?
(3)某大米包装袋上标注着“净含
量:10 kg ± 150 g”,这里的
“10 kg ±150 g”表示什么?
探索新知
解:(1)沿顺时针方向转了 12圈记作-12圈;
(2)-0.03 g表示乒乓球的质量低于标准质量0.03 g;
(3)每袋大米的标准质量应为10 kg,但实际每袋大米
可能有150 g的误差,即每袋大米的净含量最多
是10 kg+150 g,最少是10 kg-150 g.
典题精讲
1 如果水位升高6 m时水位变化记作+6m,那么水位下降6 m时水位变化记作( )
A.-3 m B.3 m
C.6 m D.-6 m
D
(来自《典中点》)
2 如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数,从轻重的角度看,最接近标准的是( )
C
探索新知
3
知识点
有理数及其分类
1.定义:整数和分数统称有理数.
要点精析:
(1)一个有理数不是整数就是分数.
(2)如果一个数既不是整数也不是分数,那么它一定不是有理数.
探索新知
2. 整数和分数:正整数、0、负整数统称为整数.
正分数、负分数统称为分数.
要点精析:几种常用整数和分数名词的含义:
(1)正整数:既是正数,又是整数的数;
(2)负整数:既是负数,又是整数的数;
(3)正分数:既是正数,又是分数的数;
(4)负分数:既是负数,又是分数的数;
(5)非负整数:正整数和0;
(6)非正整数:0和负整数.
探索新知
3.有理数的分类:
(1)按定义分类:
有理数
整数
分数
正整数
0
负整数
正分数
负分数
探索新知
(2)按性质分类:
拓展:非负整数包括正整数和0;非正整数包括负整数和0.
要点精析:在进行有理数分类时,要严格按照
同一分类标准,做到不重复不遗漏.
有理数
正有理数
负有理数
正整数
0
正分数
负整数
负分数
探索新知
例3 〈易错题〉 把下列各数分别填入相应的集合
里:-2,0,-0.314,25%,11,
非负有理数集合:{ …};
整数集合:{ …};
自然数集合:{ …};
分数集合:{ …};
非正整数集合:{ …}.
探索新知
导引:要严格按照各类数的概念进行填写,非负有理数包含正有理数和0;非正整数包含负整数和0.
典题精讲
将下列各数填入如图所示的相应的圈内.
正数集合 整数集合 负数集合
学以致用
小试牛刀
1.大于______的数叫做正数;正数是通过与________比较大小来定义的.在正数前面加上符号“-”(负)的数叫做________.负数是相对于________来定义的,只有在正数前面加上______号,所得的数才是负数;在0或负数前面加上负号,所得的数不是负数.
0
0
负数
正数
负
2.相反意义的量必须包含两层含义:第一是具有相反意义;第二是具有一定的量,但不要求数量一定相等.
例:温度上升8 ℃和温度下降5 ℃,具有相反意义的量是:____________和____________.我们可用________和________分别表示在同一问题中出现的具有相反意义的量.
上升8 ℃
正数
下降5 ℃
负数
小试牛刀
3.__________、__________、________统称为整数,________和________统称为分数,________和________统称为有理数.
负整数
负分数
整数
分数
正整数
0
正分数
4.定义:A={b,c,a},B={c},A∪B={a,b,c}.若M={-1},N={0,1,-1},则M∪N={____________}.
-1,0,1
小试牛刀
5.在-3,1.5, , ,-7,0, 中,负数一共有( )
A.1个 B.2个 C.3个 D.4个
6.下列各数中比1大的数是( )
A.2 B.0 C.-1 D.-3
A
C
7.如果向北走6步记作+6步,那么向南走8步记作( )
A.+8步 B.-8步
C.+14步 D.-2步
B
小试牛刀
8.《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是:今有两数若其意义相反,则分别叫做正数与负数.若气温为零上10 ℃记作+10 ℃,则-3 ℃表示气温为( )
A.零上3 ℃ B.零下3 ℃
C.零上7 ℃ D.零下7 ℃
B
小试牛刀
9.下列说法不正确的是( )
A.π既是正数、分数,也是有理数
B.0既不是正数,也不是负数,但是整数
C.-100既是负数,也是整数,同时是有理数
D.0既是非负数,也是非正数
A
小试牛刀
10.把下列各数填入相应的大括号里:
,0.618,-3.14,26,-2, ,0,70%,-π.
正分数:{ …};
整数:{ …};
非负数:{ …};
26,-2,0
0.618, ,70%
0.618 ,26, ,0,70%
负数:{ …};
负有理数:{ …};
有理数:{ …}.
-13,-3.14,-2,-π
-13,-3.14,-2
-13,0.618,-3.14,26,-2, ,0,70%
小试牛刀
11.指出下列各题中正负数表示的意义:
(1)水面上升-8 m;
(2)一个玻璃杯口的直径比标准尺寸大-0.01 mm;
(3)在电视上看到的天气预报,武汉某天的气温为-3 ℃~8 ℃.
解:(2)一个玻璃杯口的直径比标准尺寸小0.01 mm;
解:(1)水面下降8 m;
解:(3)武汉某天的气温在零下3 ℃与8 ℃之间.
小试牛刀
12.有一次同学聚会,小王的座位号与下列一组数中的负数的个数相等,小李的座位号与下列一组数中正整数的个数相等.
数:5, ,0,-100, ,-4.11,-0.01,53, ,-10%,+200,-20.
(1)问小王、小李的座位号各是多少?
(2)若这次同学聚会的人数是小王座位号的2倍与小李座位号的4的和,问这次聚会到了多少名同学?
解:(1)小王的座位号是7,小李的座位号是3.
解:(2)2×7+4×3=14+12=26(名).
答:这次聚会到了26名同学.
小试牛刀
13.将一串有理数按如图所示规律排列,回答下列问题:
(1)在A位置的数是正数还是负数?
解:在A位置的数是正数.
(2)A,B,C,D中哪些位置的数是负数?
(3)第2 018个数是正数还是负数?排在对应于A,B,C,D中的哪个位置?
解:(2)18 (2)B和D位置的数是负数.
解:(3)第2 018个数是正数,排在对应于C的位置.
小试牛刀
【思路点拨】要分析以下3个规律:
(1)上方的数A,B的符号与箭头指向的规律;
(2)偶数为正,奇数为负;
(3)A,B,C,D对应数的规律.
课堂小结
课堂小结
判断具有相反意义的量的方法:
(1)成对出现:具有相反意义的量是成对出现的,且必须是同类量.
(2)单位一致:两个具有相反意义的量在数量上可以不相等,但单位必须一致.
注意:用正数、负数表示相反意义的量时,哪种意
义为正没有硬性规定,并不是一成不变的.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
