北师大版(新)七上-2.3绝对值 第二课时【优质课件】
文档属性
| 名称 | 北师大版(新)七上-2.3绝对值 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览











文档简介
(共45张PPT)
2.3 绝对值
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
旧知回顾
1、什么是数轴?
数轴是规定了原点、正方向、单位长度的直线
2、什么是相反数?
只有符号不同的两个数叫做互为相反数.
规定:0的相反数是0.
数轴的三要素
0
1
2
-1
-2
新课精讲
探索新知
1
知识点
绝对值的定义
两辆汽车从同一处O出发,分别向东、西方向行驶10 km,到达A,B 两处(下图).它们的行驶路线相同吗?它们的行驶路程相等吗?说说你的想法.
探索新知
0
1
2
3
4
-1
-2
-3
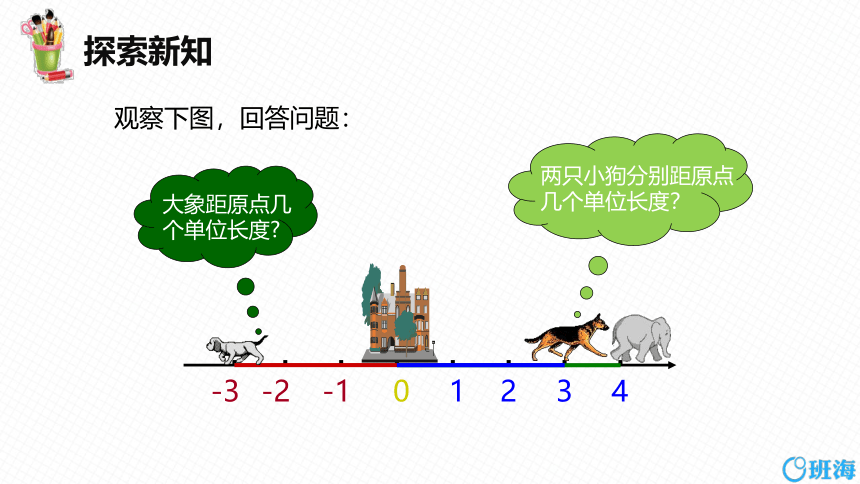
大象距原点几个单位长度
两只小狗分别距原点几个单位长度?
观察下图,回答问题:
探索新知
一般地,数轴上表示数a的点与原点的距离叫做数a 的绝对值,记作|a | . (这里的数a可以是正数、负数和0).
定义
1.几何定义:一般地,数轴上表示数a的点与原点的距离叫做数a 的绝对值,记作
2.代数定义:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0;任意一个数的绝对值为唯一非负数.
用式子表示为:
探索新知
导引:
例1 写出下列各数的绝对值:
,0, , ,-4.5,-5.
探索新知
总 结
求一个数的绝对值的方法:去掉绝对值符号时,必须按照“先判后去”的原则,先判断这个数是正数、0或负数,再根据绝对值的意义去掉绝对值符号,总之要确保其结果为非负数且只有一个.
探索新知
例2 已知一个数的绝对值是4,则这个数是________.
所以绝对值等于4的数有两个.
探索新知
总 结
直接求一个数的绝对值是一个解;若已知一个数的绝对值,反过来求这个数,则有两个解.即如果|x|=a(a>0),则x=±a.
探索新知
例3 求下列各数的绝对值:
解:
典题精讲
1 数轴上表示-2的点与原点的距离是 ________.
2 -5的绝对值是( )
A.-5 B.- C. D.5
2
D
3 的相反数是( )
A. B.- C.3 D.-3
B
探索新知
2
知识点
绝对值的性质
想一想:
互为相反数的两个数的绝对值有什么关系
0
-4
-3
-2
-1
3
2
1
原点
-3到原点的距离是3
+3到原点的距离是3
互为相反数的两个数的绝对值相等.
探索新知
1. 一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.即
(1)如果a>0,那么
(3)如果a<0,那么
2.非负性:任何有理数的绝对值都是非负数,即
(2)如果a=0,那么
探索新知
例4 下列各式中无论m为何值,一定是正数的是 ( )
A. B. C. +1 D.-(-m)
不符合题意;选项D中-(-m)
C
=m显然不符合题意;选项C中,因为
探索新知
例5 已知 ,求x与y的相反数.
探索新知
总 结
本题运用了巧用非负性技巧,考查了非负数的性质,
该性质可巧记为“0+0=0”,可以推广为:如果几个非
负数的和为0,那么这几个非负数均为0.
探索新知
例6 已知 ,求a、b 的值.
典题精讲
总 结
若几个非负数的和为0,则这几个数都为0.
典题精讲
绝对值最小的数是________;绝对值最小的负整数是________.
2 如果 +|b-1|=0,那么a+b=( )
A. B. C. D.1
0
-1
C
3 若|a-1|=a-1,则a的取值范围是( )
A.a≥1 B.a≤1 C.a<1 D.a>1
A
典题精讲
4 写出下列各式的值,并回答问题.
15
2.5
15
2.5
>
>
≥
典题精讲
5 检验4个工件,其中超过标准质量的克数记作正数,不足标准质量的克数记为负数,从轻重的角度看,最接近标准的工件是( )
A.-2 B.-3 C.3 D.5
A
探索新知
3
知识点
有理数的大小比较
做一做:
(1)在数轴上表示下列各数,并比较它们的大小:
-1.5, -3, -1, -5.
(2)求出(1)中各数的绝对值,并比较它们的大小;
(3)你发现了什么?
利用绝对值比较两个负数的大小的方法:两个负数比较大小,绝对值大的反而小.
探索新知
用数轴比较两数的大小:
1. 在数轴上表示两个数,右边的数总比左边的数大.
2. 利用数轴比较大小关键有两步:
一是在数轴上标点;
二是观察表示数的点在数轴上的位置.
有理数大小比较法则:
正数都大于零,负数都小于零, 正数都大于负数.
探索新知
例7 比较下列每组数的大小:
(1) -1和-5; (2)
解:(1)因为 |-1 |=1, |- 5 |=5, 1<5,
所以-1 > - 5;
(2)因为
所以
还可以怎么比较?
探索新知
比较两个负数大小的步骤:第一步:分别求出两个负数的绝对值;第二步:比较求出的绝对值的大小;第三步:利用绝对值比较有理数大小的法则进行判断.
总 结
典题精讲
1 已知有理数a,b在数轴上的位置如图,下列结论错误的是( )
A.|a|<1<|b| B.1<-a<b
C.1<|a|<b D.-b<a<-1
A
典题精讲
2 下列说法正确的是( )
A.一个数的绝对值一定比0大
B.一个数的相反数一定比它本身小
C.绝对值等于它本身的数一定是正数
D.最小的正整数是1
D
学以致用
小试牛刀
1.数轴上表示数a的点与原点的________,叫做数a的绝对值,记作________,读作______________.
距离
|a|
a的绝对值
2.一个正数的绝对值是它________;
一个负数的绝对值是它的__________;
________的绝对值是0.
任何数都有且只有一个绝对值;互为相反数的两数绝对值________,任何数的绝对值不可能是_____数.
本身
相反数
0
相等
负
小试牛刀
3.有理数比较大小的规定:
(1)正数______0,0______负数,正数______负数.
(2)两个负数比较大小,绝对值大的__________.
大于
大于
大于
反而小
4.如图,数轴上点A所表示的数的绝对值为( )
A.2 B.-2
C.±2 D.以上均不对
A
小试牛刀
5.点M,N,P,Q在数轴上的位置如图所示,其中表示的数的绝对值最大的点是( )
A.M B.N C.P D.Q
D
6.化简:|-15|等于( )
A.15 B.-15 C.±15 D.
A
小试牛刀
7.若|x|=4,则x的值是( )
A.4 B.-4 C.±4 D.
8.若|a-1|=a-1,则a的取值范围是( )
A.a≥1 B.a≤1 C.a<1 D.a>1
A
C
9.若a,b为有理数,a>0,b<0且|a|<|b|,那么a,b,-a,-b的大小关系是( )
A.b<-a<-bC.b<-aC
小试牛刀
10.如果-a的相反数是最小的正整数,b是绝对值最小的数,求a+b的值.
解:由题意知a=1,b=0,所以a+b=1+0=1.
11.在三个有理数a,b,c中,a,b都是负数,c是正数,且|b|>|a|>|c|.
(1)在数轴上表示出a,b,c三个数所对应的点的大致位置;
(2)比较a,b,c的大小.
解:(1)如图所示.
小试牛刀
12.有理数a,b,c在数轴上对应点的位置如图所示.
(1) 在横线上填入“>”或“<”:
a______0,b______0,c______0,|c|______|a|;
<
<
>
>
(2)试在数轴上找出表示-a,-b,-c的点;
(3)试用“<”将a,-a,b,-b,c,-c,0连接起来.
解: (2)如图所示.
(3)c<-b<a<0<-a<b<-c.
小试牛刀
13.北京航天研究院所属工厂制造“嫦娥三号”上的一种螺母,要求螺母内径可以有±0.02 mm的误差.抽查5个螺母,超过规定内径的毫米数记作正数,检查结果如下:
+0.010,-0.018,+0.006,-0.002,+0.015.
(1)指出哪些产品是合乎要求的(即在误差范围内);
解:因为|+0.010|=0.010<0.02,|-0.018|=0.018<0.02,|+0.006|=0.006<0.02,|-0.002|=0.002<0.02,|+0.015|=0.015<0.02,所抽查的产品都在误差范围内,
所以都合乎要求.
小试牛刀
(2)指出合乎要求的产品哪个质量最好,哪个质量最差.
解:绝对值越接近0,即绝对值越小,质量越好,所以结果为-0.002的产品质量最好,结果为-0.018的产品质量最差.
小试牛刀
14.阅读: =1- ;
= - ;
= - ;…
若|xy-2|+|y-1|=0,试求 + +
+ …+ 的值.
【思路点拨】先利用“若|a|+|b|=0,则a=0,b=0”,求出x,y的值,再代入用裂项相消法计算.
小试牛刀
解:因为|xy-2|+|y-1|=0,
|xy-2|≥0,|y-1|≥0,
所以|xy-2|=0,|y-1|=0.
所以xy=2,y=1.
所以x=2.
小试牛刀
原式= + + + …+
= + + +…+
=(1- )+( - )+( - )
+ …+( - )= 1 -
=
课堂小结
课堂小结
相反数的意义:
代数意义:(1)成对出现;(2)只有符号不同,即a 的相反数是-a;特殊地:0的相反数是0.
几何意义:数轴上原点两旁且到原点距离相等的两个点所表示的数互为相反数.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
2.3 绝对值
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
旧知回顾
1、什么是数轴?
数轴是规定了原点、正方向、单位长度的直线
2、什么是相反数?
只有符号不同的两个数叫做互为相反数.
规定:0的相反数是0.
数轴的三要素
0
1
2
-1
-2
新课精讲
探索新知
1
知识点
绝对值的定义
两辆汽车从同一处O出发,分别向东、西方向行驶10 km,到达A,B 两处(下图).它们的行驶路线相同吗?它们的行驶路程相等吗?说说你的想法.
探索新知
0
1
2
3
4
-1
-2
-3
大象距原点几个单位长度
两只小狗分别距原点几个单位长度?
观察下图,回答问题:
探索新知
一般地,数轴上表示数a的点与原点的距离叫做数a 的绝对值,记作|a | . (这里的数a可以是正数、负数和0).
定义
1.几何定义:一般地,数轴上表示数a的点与原点的距离叫做数a 的绝对值,记作
2.代数定义:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0;任意一个数的绝对值为唯一非负数.
用式子表示为:
探索新知
导引:
例1 写出下列各数的绝对值:
,0, , ,-4.5,-5.
探索新知
总 结
求一个数的绝对值的方法:去掉绝对值符号时,必须按照“先判后去”的原则,先判断这个数是正数、0或负数,再根据绝对值的意义去掉绝对值符号,总之要确保其结果为非负数且只有一个.
探索新知
例2 已知一个数的绝对值是4,则这个数是________.
所以绝对值等于4的数有两个.
探索新知
总 结
直接求一个数的绝对值是一个解;若已知一个数的绝对值,反过来求这个数,则有两个解.即如果|x|=a(a>0),则x=±a.
探索新知
例3 求下列各数的绝对值:
解:
典题精讲
1 数轴上表示-2的点与原点的距离是 ________.
2 -5的绝对值是( )
A.-5 B.- C. D.5
2
D
3 的相反数是( )
A. B.- C.3 D.-3
B
探索新知
2
知识点
绝对值的性质
想一想:
互为相反数的两个数的绝对值有什么关系
0
-4
-3
-2
-1
3
2
1
原点
-3到原点的距离是3
+3到原点的距离是3
互为相反数的两个数的绝对值相等.
探索新知
1. 一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.即
(1)如果a>0,那么
(3)如果a<0,那么
2.非负性:任何有理数的绝对值都是非负数,即
(2)如果a=0,那么
探索新知
例4 下列各式中无论m为何值,一定是正数的是 ( )
A. B. C. +1 D.-(-m)
不符合题意;选项D中-(-m)
C
=m显然不符合题意;选项C中,因为
探索新知
例5 已知 ,求x与y的相反数.
探索新知
总 结
本题运用了巧用非负性技巧,考查了非负数的性质,
该性质可巧记为“0+0=0”,可以推广为:如果几个非
负数的和为0,那么这几个非负数均为0.
探索新知
例6 已知 ,求a、b 的值.
典题精讲
总 结
若几个非负数的和为0,则这几个数都为0.
典题精讲
绝对值最小的数是________;绝对值最小的负整数是________.
2 如果 +|b-1|=0,那么a+b=( )
A. B. C. D.1
0
-1
C
3 若|a-1|=a-1,则a的取值范围是( )
A.a≥1 B.a≤1 C.a<1 D.a>1
A
典题精讲
4 写出下列各式的值,并回答问题.
15
2.5
15
2.5
>
>
≥
典题精讲
5 检验4个工件,其中超过标准质量的克数记作正数,不足标准质量的克数记为负数,从轻重的角度看,最接近标准的工件是( )
A.-2 B.-3 C.3 D.5
A
探索新知
3
知识点
有理数的大小比较
做一做:
(1)在数轴上表示下列各数,并比较它们的大小:
-1.5, -3, -1, -5.
(2)求出(1)中各数的绝对值,并比较它们的大小;
(3)你发现了什么?
利用绝对值比较两个负数的大小的方法:两个负数比较大小,绝对值大的反而小.
探索新知
用数轴比较两数的大小:
1. 在数轴上表示两个数,右边的数总比左边的数大.
2. 利用数轴比较大小关键有两步:
一是在数轴上标点;
二是观察表示数的点在数轴上的位置.
有理数大小比较法则:
正数都大于零,负数都小于零, 正数都大于负数.
探索新知
例7 比较下列每组数的大小:
(1) -1和-5; (2)
解:(1)因为 |-1 |=1, |- 5 |=5, 1<5,
所以-1 > - 5;
(2)因为
所以
还可以怎么比较?
探索新知
比较两个负数大小的步骤:第一步:分别求出两个负数的绝对值;第二步:比较求出的绝对值的大小;第三步:利用绝对值比较有理数大小的法则进行判断.
总 结
典题精讲
1 已知有理数a,b在数轴上的位置如图,下列结论错误的是( )
A.|a|<1<|b| B.1<-a<b
C.1<|a|<b D.-b<a<-1
A
典题精讲
2 下列说法正确的是( )
A.一个数的绝对值一定比0大
B.一个数的相反数一定比它本身小
C.绝对值等于它本身的数一定是正数
D.最小的正整数是1
D
学以致用
小试牛刀
1.数轴上表示数a的点与原点的________,叫做数a的绝对值,记作________,读作______________.
距离
|a|
a的绝对值
2.一个正数的绝对值是它________;
一个负数的绝对值是它的__________;
________的绝对值是0.
任何数都有且只有一个绝对值;互为相反数的两数绝对值________,任何数的绝对值不可能是_____数.
本身
相反数
0
相等
负
小试牛刀
3.有理数比较大小的规定:
(1)正数______0,0______负数,正数______负数.
(2)两个负数比较大小,绝对值大的__________.
大于
大于
大于
反而小
4.如图,数轴上点A所表示的数的绝对值为( )
A.2 B.-2
C.±2 D.以上均不对
A
小试牛刀
5.点M,N,P,Q在数轴上的位置如图所示,其中表示的数的绝对值最大的点是( )
A.M B.N C.P D.Q
D
6.化简:|-15|等于( )
A.15 B.-15 C.±15 D.
A
小试牛刀
7.若|x|=4,则x的值是( )
A.4 B.-4 C.±4 D.
8.若|a-1|=a-1,则a的取值范围是( )
A.a≥1 B.a≤1 C.a<1 D.a>1
A
C
9.若a,b为有理数,a>0,b<0且|a|<|b|,那么a,b,-a,-b的大小关系是( )
A.b<-a<-bC.b<-a
小试牛刀
10.如果-a的相反数是最小的正整数,b是绝对值最小的数,求a+b的值.
解:由题意知a=1,b=0,所以a+b=1+0=1.
11.在三个有理数a,b,c中,a,b都是负数,c是正数,且|b|>|a|>|c|.
(1)在数轴上表示出a,b,c三个数所对应的点的大致位置;
(2)比较a,b,c的大小.
解:(1)如图所示.
小试牛刀
12.有理数a,b,c在数轴上对应点的位置如图所示.
(1) 在横线上填入“>”或“<”:
a______0,b______0,c______0,|c|______|a|;
<
<
>
>
(2)试在数轴上找出表示-a,-b,-c的点;
(3)试用“<”将a,-a,b,-b,c,-c,0连接起来.
解: (2)如图所示.
(3)c<-b<a<0<-a<b<-c.
小试牛刀
13.北京航天研究院所属工厂制造“嫦娥三号”上的一种螺母,要求螺母内径可以有±0.02 mm的误差.抽查5个螺母,超过规定内径的毫米数记作正数,检查结果如下:
+0.010,-0.018,+0.006,-0.002,+0.015.
(1)指出哪些产品是合乎要求的(即在误差范围内);
解:因为|+0.010|=0.010<0.02,|-0.018|=0.018<0.02,|+0.006|=0.006<0.02,|-0.002|=0.002<0.02,|+0.015|=0.015<0.02,所抽查的产品都在误差范围内,
所以都合乎要求.
小试牛刀
(2)指出合乎要求的产品哪个质量最好,哪个质量最差.
解:绝对值越接近0,即绝对值越小,质量越好,所以结果为-0.002的产品质量最好,结果为-0.018的产品质量最差.
小试牛刀
14.阅读: =1- ;
= - ;
= - ;…
若|xy-2|+|y-1|=0,试求 + +
+ …+ 的值.
【思路点拨】先利用“若|a|+|b|=0,则a=0,b=0”,求出x,y的值,再代入用裂项相消法计算.
小试牛刀
解:因为|xy-2|+|y-1|=0,
|xy-2|≥0,|y-1|≥0,
所以|xy-2|=0,|y-1|=0.
所以xy=2,y=1.
所以x=2.
小试牛刀
原式= + + + …+
= + + +…+
=(1- )+( - )+( - )
+ …+( - )= 1 -
=
课堂小结
课堂小结
相反数的意义:
代数意义:(1)成对出现;(2)只有符号不同,即a 的相反数是-a;特殊地:0的相反数是0.
几何意义:数轴上原点两旁且到原点距离相等的两个点所表示的数互为相反数.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
