北师大版(新)七上-2.5 有理数的减法【优质课件】
文档属性
| 名称 | 北师大版(新)七上-2.5 有理数的减法【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:52:22 | ||
图片预览







文档简介
(共36张PPT)
2.5 有理数的减法
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1、有理数的加法法则是什么?
2、填空:
(1)16-7= ______,
(2)
复
习
回
顾
9
新课精讲
探索新知
1
知识点
有理数的减法法则
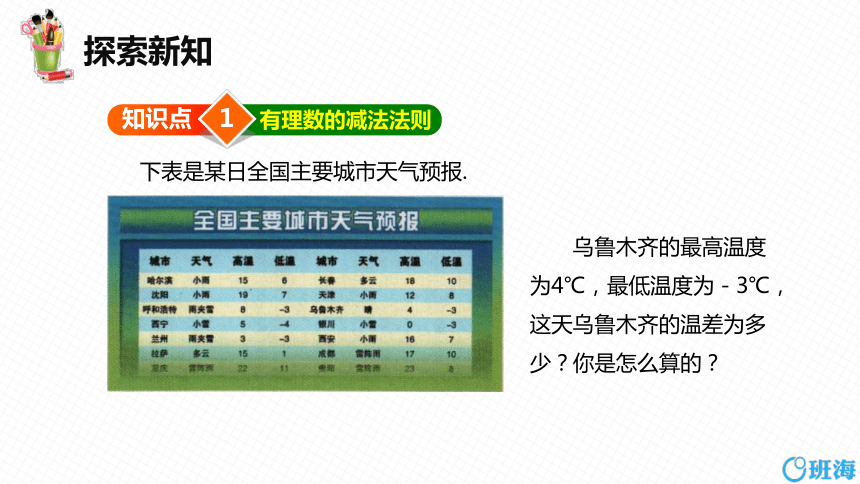
下表是某日全国主要城市天气预报.
乌鲁木齐的最高温度为4℃,最低温度为-3℃,
这天乌鲁木齐的温差为多少?你是怎么算的?
探索新知
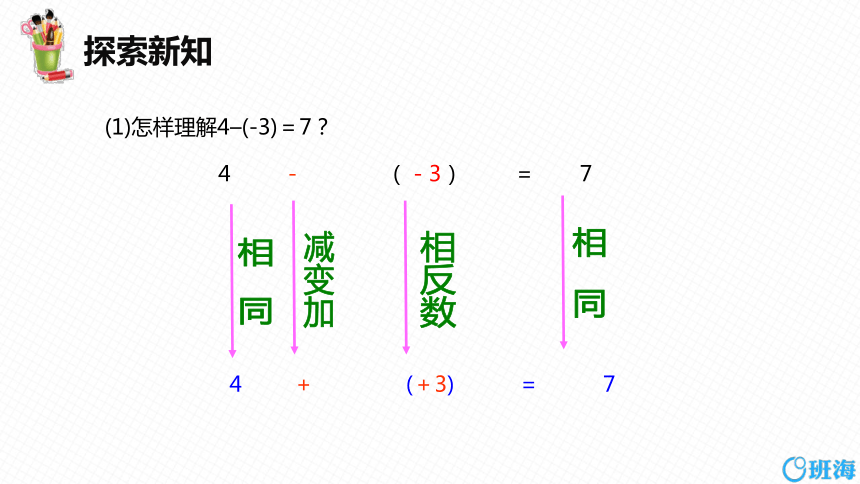
(1)怎样理解4–(-3)=7?
4 - (-3) = 7
4 + (+3) = 7
相 同
减变加
相反数
相 同
探索新知
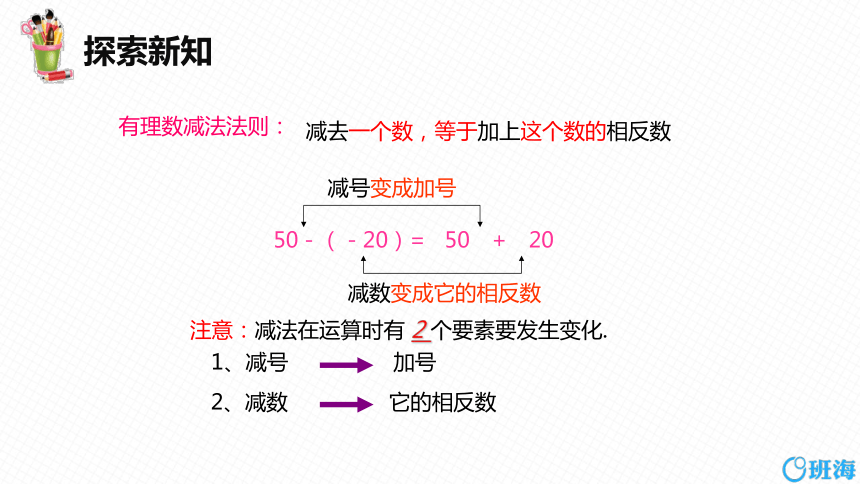
减去一个数,等于加上这个数的相反数
有理数减法法则:
注意:减法在运算时有 2 个要素要发生变化.
1、减号
加号
它的相反数
2、减数
50-(-20)= 50 + 20
减号变成加号
减数变成它的相反数
探索新知
有理数减法法则:减去一个数,等于加这个数的 相反数;
即:a-b=a+(-b).
这里a和b可以是正,也
可以是负,还可以为0
由此可见,有理数的减法运算实质转化为加法运算.
转化的思想方法
探索新知
减法运算步骤:
(1)变减法运算为加法运算,做到“两变一不变”, “两变”中一变运算符号,减号变加号;二变减数,减数变为它的相反数;“一不变”被减数不变;
(2)运用加法法则进行计算.
探索新知
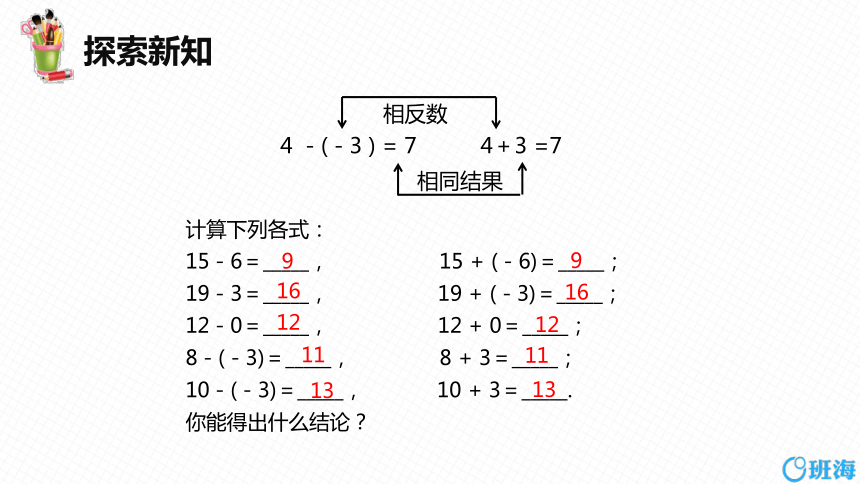
相同结果
4 -(-3 ) = 7 4+3 =7
相反数
计算下列各式:
15-6=_____, 15 + (-6)=_____;
19-3=_____, 19 + (-3)=_____;
12-0=_____, 12 + 0=_____;
8-(-3)=_____, 8 + 3=_____;
10-(-3)=_____, 10 + 3=_____.
你能得出什么结论?
13
9
16
12
11
13
12
11
16
9
探索新知
例1 计算下列各题:
(1)9-(-5); (2)(-3)-1;
(3)0-8; (4)(-5)-0.
解:(1) 9-(-5) = 9+5=14;
(2)(-3)-1 = (-3) + (-1) = -4;
(3)0-8 = 0+ (-8) = -8;
(4)(-5)-0 =-5.
探索新知
从本例中,我们必须明确两点:一是进行有理数减法运算的关键在于利用法则变减法为加法;二是有理数减法不能直接进行计算,只有转化为加法后才能进行计算.
总 结
典题精讲
1 在下列横线上填上适当的数.
(1)(-8)-(-6)=(-8)+(________);
(2)(-3)-4=(-3)+(________);
(3) =0+(________);
(4)8-2 016=8+(________).
6
-4
-2016
4 如图,数轴上A点表示的数减去B点表示的数,结果是( )
A.8 B.-8 C.2 D.-2
B
典题精讲
2 计算: 等于( )
A. B.
C. D.
3 与(-x)-(-y)相等的式子是( )
A.(-x)-(+y) B.(+x)+(-y)
C.(-x)+y D.(+x)-(-y)
C
C
探索新知
例2 世界上最高的山峰是珠穆朗玛峰,其海拔高度大约是8 844 m,吐鲁番盆地的海拔高度大约是-155 m. 两处高度相差多少米?
解: 8 844 -(-155)
=8 844+155
=8 999(m).
因此,两处高度相差8 999 m.
2
知识点
有理数减法法则的运用
8 844 m有
多少层楼高?
探索新知
例3 全班学生分为五个组进行游戏,每组的基本分为100分,答对一题 加50分,答错一题扣50分.游戏结束时,各组的分数如下:
(1)第一名超出第二名多少分?
(2)第一名超出第五名多少分?
第1组 第2组 第3组 第4组 第5组
100 150 -400 350 -100
探索新知
解:由上表可以看出,第一名得了 350分,第二名得了 150分,第五名得 了-400 分.
(1)350 -150 =200(分);
(2) 350-(-400) =750(分).
因此,第一名超出第二名200分,第一名超出第五名750分.
探索新知
例4 A,B是数轴上的两点,A表示的数是-5,A,B两点之间的距离为6,求B点所表示的数.
解:方法一:画出数轴如图,
距A点6个单位长度的点 有两个,
分别为点B′,B″,所表示的数分别为-11和1.
所以B点所表示的数为-11或1.
探索新知
方法二:因为数轴上两点之间的距离等于这两点所表示的数的差的绝对值,一个点表示的数是-5,
设另一个点表示的数为x.
所以|-5-x|=6.
所以-5-x=6或-5-x=-6.
所以x=-11或x=1.
所以B点所表示的数为-11或1.
探索新知
方法一充分体现了数形结合思想,很直观;方法二直接套用两点间的距离公式较简单,解题时,要注意灵活选用解题方法或采用多种方法解题,以扩大自己的知识视野.
总 结
典题精讲
1 若a为负数,则a减去它的相反数等于( )
A.0 B.2a
C.-2a D.2a或-2a
2 若m<0,则|m-(-m)|等于( )
A.2m B.-2m
C.2m或-2m D.以上都有可能
B
B
典题精讲
3 有理数a,b在数轴上所对应的点的位置如图所示,则a-b的值在( )
A.-3与-2之间 B.-2与-1之间
C.0与1之间 D.2与3之间
D
4 桂林冬季里某一天最高气温是7 ℃,最低气温是-1 ℃,这一天桂林的温差是( )
A.-8 ℃ B.6 ℃
C.7 ℃ D.8 ℃
D
学以致用
小试牛刀
1.有理数的减法法则:减去一个数,等于________这个数的________.
其实质是:变减法运算为______运算,要做到“两变”:一变运算符号,即减号变成加号;二变减数,即减数变成它的相反数.
加上
相反数
加法
2.求数轴上两点间的距离的方法:一、利用数轴求;二、利用有理数的减法,先比较两数的大小,然后用较大的数减去较小的数,如:数轴上-5与3对应的点之间的距离为:3-(-5)=________.
8
小试牛刀
3.在横线上填上适当的数或式子:
(1)-3-(-1)=(-3)+________;
(2)-4-2=(-4)+________;
(3)0-(-2.7)=0+________;
(4)5-(+2 017)=__________________.
1
(-2)
2.7
5+(-2 017)
4.如图,数轴上A点表示的数减去B点表示的数,结果是( )
A.8 B.-8 C.2 D.-2
D
小试牛刀
5.计算3-(-1)的结果是( )
A.-4 B.-2 C.2 D.4
6.3-π的绝对值是( )
A.3-π B.π-3 C.3 D.π
D
7.有理数a,b在数轴上对应的点的位置如图所示,计算|a-b|的结果为( )
A.a+b B.a-b
C.-a+b D.-a-b
C
B
小试牛刀
8.我市冬季里某一天的最低气温是-10 ℃,最高气温是5 ℃,这一天的温差为( )
A.-5 ℃ B.5 ℃
C.10 ℃ D.15 ℃
D
9.有理数a,b在数轴上的对应点的位置如图所示,则( )
A.a+b>0 B.a+b<0
C.a-b<0 D.a-b=0
A
小试牛刀
10.计算:
(1)(+2)-(+8); (2)(-16)-(+45);
(3)0-(-7); (4)(+25)-(-13).
=2+(-8)=-6
=(-16)+(-45)=-61
=0+7=7
=25+13=38
小试牛刀
11.根据题意列出式子,并计算:
(1)一个加数是1.8,和是-0.81,求另一个加数;
(2) 的绝对值的相反数与 的相反数的差.
解:(1)-0.81-1.8=-2.61
(2)-| |- = + = .
小试牛刀
12.已知有理数a,b,c在数轴上的对应点的位置如图所示.
(1)判断下列各式的符号:a-b,b-c,c-a;
解:a-b<0,b-c<0,c-a>0.
(2)若|a|=2,|b|=,|c|=1,试比较c-b与b-a之间的大小关系.
解:由数轴及题意可得a=-2,b=-12,c=1,
所以c-b=1--12=32,b-a=-12-(-2)=32.
所以c-b=b-a.
小试牛刀
13.王明同学连续记录了一周内每天的最高气温和最低气温,其数据如下表(单位:℃):
星期 一 二 三 四 五 六 日
最高气温 -3 6 8 -2 5 3 11
最低气温 -9 -4 -3 -13 -4 -6 -1
由表中数据分析:本周内气温最高是多少?气温最低是多少?哪天的温差最大?温差最大是多少?
解:本周内气温最高是11 ℃,气温最低是-13 ℃,周日的温差最大,温差最大是11-(-1)=12(℃).
小试牛刀
14.阅读:|5-2|表示5与2的差的绝对值,也可理解为5与2两个数在数轴上所对应的两点之间的距离;|5+2|可以看成|5-(-2)|,表示5与-2的差的绝对值,也可理解为5与-2两个数在数轴上所对应的两点之间的距离.探索:
(1)求|5-(-2)|的值;
解:|5-(-2)|=7.
(2)利用数轴,找出所有符合条件的整数x(不包括5和-2),使x所对应的点到5和-2两个数所对应的点的距离之和为7.
【思路点拨】由于数轴上5和-2对应的点之间的距离为7,因此到5和-2两个数所对应的点的距离之和为7的点都在数轴上5和-2对应的点之间.
解:x为4,3,2,1,0,-1.
课堂小结
课堂小结
有理数减法法则的实质是将减法转化为加法,其转化的方法是“两变”:
一是“变”减号为加号;
二是将减数“变”为它的相反数.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
2.5 有理数的减法
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1、有理数的加法法则是什么?
2、填空:
(1)16-7= ______,
(2)
复
习
回
顾
9
新课精讲
探索新知
1
知识点
有理数的减法法则
下表是某日全国主要城市天气预报.
乌鲁木齐的最高温度为4℃,最低温度为-3℃,
这天乌鲁木齐的温差为多少?你是怎么算的?
探索新知
(1)怎样理解4–(-3)=7?
4 - (-3) = 7
4 + (+3) = 7
相 同
减变加
相反数
相 同
探索新知
减去一个数,等于加上这个数的相反数
有理数减法法则:
注意:减法在运算时有 2 个要素要发生变化.
1、减号
加号
它的相反数
2、减数
50-(-20)= 50 + 20
减号变成加号
减数变成它的相反数
探索新知
有理数减法法则:减去一个数,等于加这个数的 相反数;
即:a-b=a+(-b).
这里a和b可以是正,也
可以是负,还可以为0
由此可见,有理数的减法运算实质转化为加法运算.
转化的思想方法
探索新知
减法运算步骤:
(1)变减法运算为加法运算,做到“两变一不变”, “两变”中一变运算符号,减号变加号;二变减数,减数变为它的相反数;“一不变”被减数不变;
(2)运用加法法则进行计算.
探索新知
相同结果
4 -(-3 ) = 7 4+3 =7
相反数
计算下列各式:
15-6=_____, 15 + (-6)=_____;
19-3=_____, 19 + (-3)=_____;
12-0=_____, 12 + 0=_____;
8-(-3)=_____, 8 + 3=_____;
10-(-3)=_____, 10 + 3=_____.
你能得出什么结论?
13
9
16
12
11
13
12
11
16
9
探索新知
例1 计算下列各题:
(1)9-(-5); (2)(-3)-1;
(3)0-8; (4)(-5)-0.
解:(1) 9-(-5) = 9+5=14;
(2)(-3)-1 = (-3) + (-1) = -4;
(3)0-8 = 0+ (-8) = -8;
(4)(-5)-0 =-5.
探索新知
从本例中,我们必须明确两点:一是进行有理数减法运算的关键在于利用法则变减法为加法;二是有理数减法不能直接进行计算,只有转化为加法后才能进行计算.
总 结
典题精讲
1 在下列横线上填上适当的数.
(1)(-8)-(-6)=(-8)+(________);
(2)(-3)-4=(-3)+(________);
(3) =0+(________);
(4)8-2 016=8+(________).
6
-4
-2016
4 如图,数轴上A点表示的数减去B点表示的数,结果是( )
A.8 B.-8 C.2 D.-2
B
典题精讲
2 计算: 等于( )
A. B.
C. D.
3 与(-x)-(-y)相等的式子是( )
A.(-x)-(+y) B.(+x)+(-y)
C.(-x)+y D.(+x)-(-y)
C
C
探索新知
例2 世界上最高的山峰是珠穆朗玛峰,其海拔高度大约是8 844 m,吐鲁番盆地的海拔高度大约是-155 m. 两处高度相差多少米?
解: 8 844 -(-155)
=8 844+155
=8 999(m).
因此,两处高度相差8 999 m.
2
知识点
有理数减法法则的运用
8 844 m有
多少层楼高?
探索新知
例3 全班学生分为五个组进行游戏,每组的基本分为100分,答对一题 加50分,答错一题扣50分.游戏结束时,各组的分数如下:
(1)第一名超出第二名多少分?
(2)第一名超出第五名多少分?
第1组 第2组 第3组 第4组 第5组
100 150 -400 350 -100
探索新知
解:由上表可以看出,第一名得了 350分,第二名得了 150分,第五名得 了-400 分.
(1)350 -150 =200(分);
(2) 350-(-400) =750(分).
因此,第一名超出第二名200分,第一名超出第五名750分.
探索新知
例4 A,B是数轴上的两点,A表示的数是-5,A,B两点之间的距离为6,求B点所表示的数.
解:方法一:画出数轴如图,
距A点6个单位长度的点 有两个,
分别为点B′,B″,所表示的数分别为-11和1.
所以B点所表示的数为-11或1.
探索新知
方法二:因为数轴上两点之间的距离等于这两点所表示的数的差的绝对值,一个点表示的数是-5,
设另一个点表示的数为x.
所以|-5-x|=6.
所以-5-x=6或-5-x=-6.
所以x=-11或x=1.
所以B点所表示的数为-11或1.
探索新知
方法一充分体现了数形结合思想,很直观;方法二直接套用两点间的距离公式较简单,解题时,要注意灵活选用解题方法或采用多种方法解题,以扩大自己的知识视野.
总 结
典题精讲
1 若a为负数,则a减去它的相反数等于( )
A.0 B.2a
C.-2a D.2a或-2a
2 若m<0,则|m-(-m)|等于( )
A.2m B.-2m
C.2m或-2m D.以上都有可能
B
B
典题精讲
3 有理数a,b在数轴上所对应的点的位置如图所示,则a-b的值在( )
A.-3与-2之间 B.-2与-1之间
C.0与1之间 D.2与3之间
D
4 桂林冬季里某一天最高气温是7 ℃,最低气温是-1 ℃,这一天桂林的温差是( )
A.-8 ℃ B.6 ℃
C.7 ℃ D.8 ℃
D
学以致用
小试牛刀
1.有理数的减法法则:减去一个数,等于________这个数的________.
其实质是:变减法运算为______运算,要做到“两变”:一变运算符号,即减号变成加号;二变减数,即减数变成它的相反数.
加上
相反数
加法
2.求数轴上两点间的距离的方法:一、利用数轴求;二、利用有理数的减法,先比较两数的大小,然后用较大的数减去较小的数,如:数轴上-5与3对应的点之间的距离为:3-(-5)=________.
8
小试牛刀
3.在横线上填上适当的数或式子:
(1)-3-(-1)=(-3)+________;
(2)-4-2=(-4)+________;
(3)0-(-2.7)=0+________;
(4)5-(+2 017)=__________________.
1
(-2)
2.7
5+(-2 017)
4.如图,数轴上A点表示的数减去B点表示的数,结果是( )
A.8 B.-8 C.2 D.-2
D
小试牛刀
5.计算3-(-1)的结果是( )
A.-4 B.-2 C.2 D.4
6.3-π的绝对值是( )
A.3-π B.π-3 C.3 D.π
D
7.有理数a,b在数轴上对应的点的位置如图所示,计算|a-b|的结果为( )
A.a+b B.a-b
C.-a+b D.-a-b
C
B
小试牛刀
8.我市冬季里某一天的最低气温是-10 ℃,最高气温是5 ℃,这一天的温差为( )
A.-5 ℃ B.5 ℃
C.10 ℃ D.15 ℃
D
9.有理数a,b在数轴上的对应点的位置如图所示,则( )
A.a+b>0 B.a+b<0
C.a-b<0 D.a-b=0
A
小试牛刀
10.计算:
(1)(+2)-(+8); (2)(-16)-(+45);
(3)0-(-7); (4)(+25)-(-13).
=2+(-8)=-6
=(-16)+(-45)=-61
=0+7=7
=25+13=38
小试牛刀
11.根据题意列出式子,并计算:
(1)一个加数是1.8,和是-0.81,求另一个加数;
(2) 的绝对值的相反数与 的相反数的差.
解:(1)-0.81-1.8=-2.61
(2)-| |- = + = .
小试牛刀
12.已知有理数a,b,c在数轴上的对应点的位置如图所示.
(1)判断下列各式的符号:a-b,b-c,c-a;
解:a-b<0,b-c<0,c-a>0.
(2)若|a|=2,|b|=,|c|=1,试比较c-b与b-a之间的大小关系.
解:由数轴及题意可得a=-2,b=-12,c=1,
所以c-b=1--12=32,b-a=-12-(-2)=32.
所以c-b=b-a.
小试牛刀
13.王明同学连续记录了一周内每天的最高气温和最低气温,其数据如下表(单位:℃):
星期 一 二 三 四 五 六 日
最高气温 -3 6 8 -2 5 3 11
最低气温 -9 -4 -3 -13 -4 -6 -1
由表中数据分析:本周内气温最高是多少?气温最低是多少?哪天的温差最大?温差最大是多少?
解:本周内气温最高是11 ℃,气温最低是-13 ℃,周日的温差最大,温差最大是11-(-1)=12(℃).
小试牛刀
14.阅读:|5-2|表示5与2的差的绝对值,也可理解为5与2两个数在数轴上所对应的两点之间的距离;|5+2|可以看成|5-(-2)|,表示5与-2的差的绝对值,也可理解为5与-2两个数在数轴上所对应的两点之间的距离.探索:
(1)求|5-(-2)|的值;
解:|5-(-2)|=7.
(2)利用数轴,找出所有符合条件的整数x(不包括5和-2),使x所对应的点到5和-2两个数所对应的点的距离之和为7.
【思路点拨】由于数轴上5和-2对应的点之间的距离为7,因此到5和-2两个数所对应的点的距离之和为7的点都在数轴上5和-2对应的点之间.
解:x为4,3,2,1,0,-1.
课堂小结
课堂小结
有理数减法法则的实质是将减法转化为加法,其转化的方法是“两变”:
一是“变”减号为加号;
二是将减数“变”为它的相反数.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
