北师大版(新)七上-4.5 多边形和圆的初步认识 第二课时【优质课件】
文档属性
| 名称 | 北师大版(新)七上-4.5 多边形和圆的初步认识 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:52:29 | ||
图片预览








文档简介
(共37张PPT)
4.5 多边形和圆的初步认识
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
圆是常见的图形,生活中的许多物体都给我们以圆的形象(如图).
新课精讲
探索新知
1
知识点
圆及相关概念
上面的图形中有我们熟悉的圆和扇形,你还记得用哪些方法可以画一个圆吗?你能用一根细绳和笔画出一个圆吗?
做一做
探索新知
圆的定义: 在一个平面内,线段OA饶它的一个端点O旋转一周,另一个端点A随之旋转所形成的的图形叫做圆. 固定的端点O叫做圆心,线段OA叫做半径.
如图:以O为圆心的圆,记作“⊙O”,读作“圆O”
探索新知
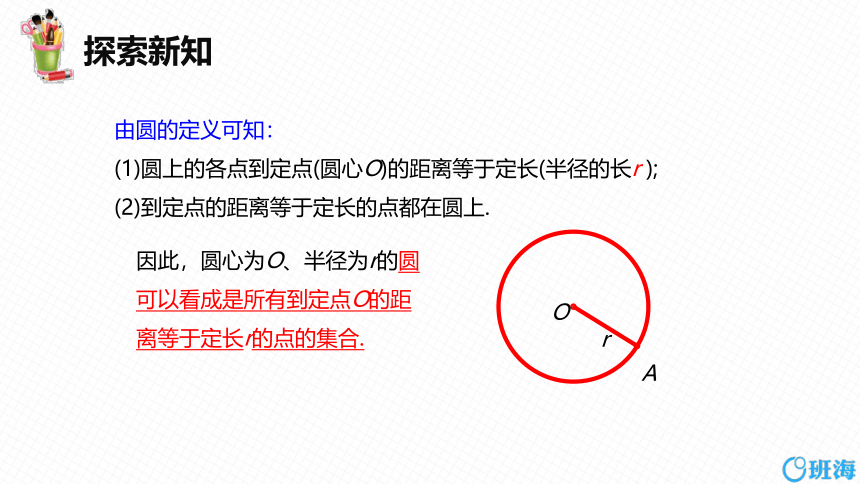
由圆的定义可知:
(1)圆上的各点到定点(圆心O)的距离等于定长(半径的长r );
(2)到定点的距离等于定长的点都在圆上.
因此,圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点的集合.
r
O
A
探索新知
O
A
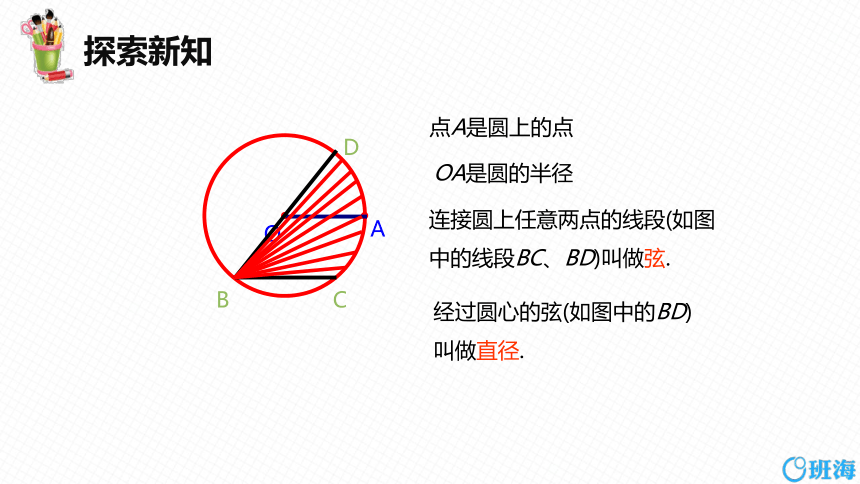
点A是圆上的点
OA是圆的半径
B
C
D
连接圆上任意两点的线段(如图中的线段BC、BD)叫做弦.
经过圆心的弦(如图中的BD)叫做直径.
探索新知
半径和直径的特点:
半径有( )条,
直径有( )条,
直径是半径的( ),
半径是直径的( ).
无数
无数
2倍
在同一个(等)圆内,
探索新知
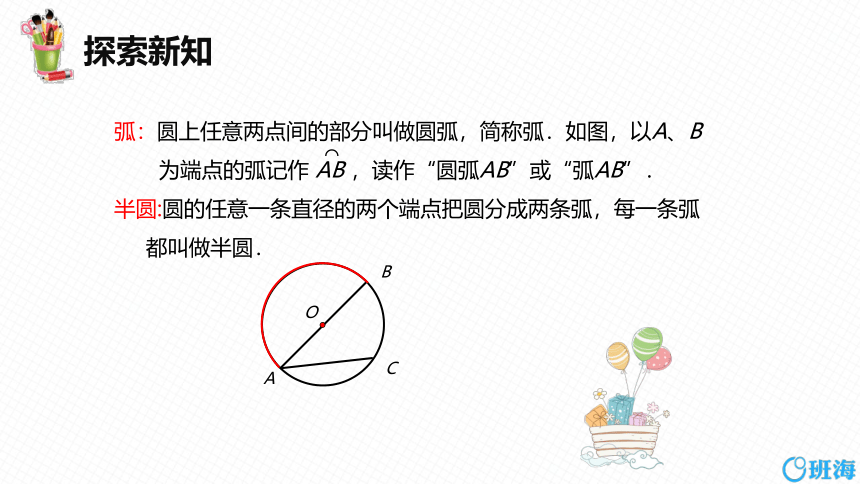
弧:圆上任意两点间的部分叫做圆弧,简称弧.如图,以A、B
为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
半圆:圆的任意一条直径的两个端点把圆分成两条弧,每一条弧
都叫做半圆.
⌒
·
C
O
A
B
探索新知
·
C
O
A
B
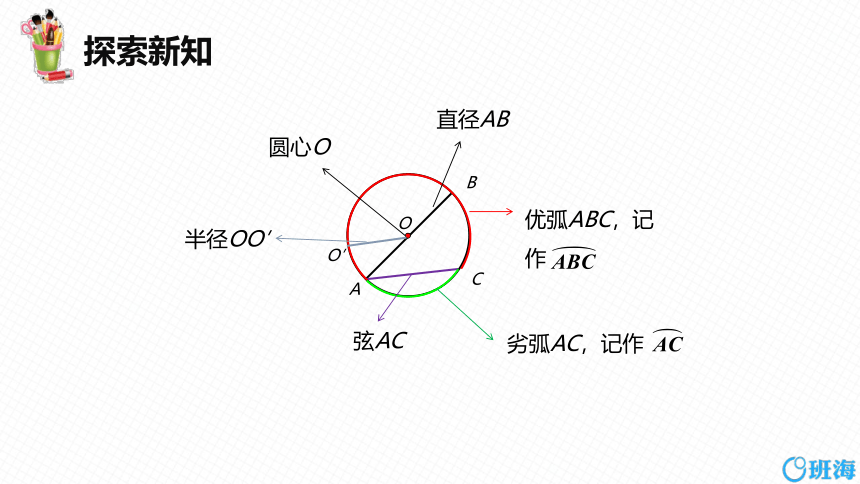
圆心O
直径AB
弦AC
优弧ABC,记作
劣弧AC,记作
O′
半径OO′
探索新知
以下命题:(1)半圆是弧,但弧不一定是半圆;(2)过圆上任意一点只能作一条弦,且这条弦是直径;(3)弦是直径;(4)直径是圆中最长的弦;(5)直径不是弦;(6)优弧大于劣弧;(7)以O为圆心可以画无数个圆. 正确的个数为( )
A.1 B.2 C.3 D.4
C
例1
探索新知
(1)半圆是弧的一种,弧可以分为劣弧、半圆、优 弧三种,故正确;(2)过圆上任意一点可以作无数条弦,故错误;(3)直径是过圆心的特殊弦,但弦不一定是直径,故错误;(4)圆有无数条弦,过圆心的弦最长,即直径是圆中最长的弦,故正确;(5)直径是圆中最长的弦,故错误;(6)在同圆或等 圆中,优弧大于劣弧,故错误;(7)以一个点为圆 心,若不指明半径,可画出无数个大小不等的同心圆,故正确.
导引:
典题精讲
平面上,一条线段绕着它固定的一个端点旋转一周,另一个端点形成的图形叫做________.固定的端点称为________,这条线段称为________.圆上任意两点间的部分叫做________,简称________.
圆
圆心
半径
圆弧
弧
2 下列条件中,能确定圆的是( )
A.以已知点O为圆心
B.以点O为圆心,2 cm为半径
C.以2 cm为半径
D.经过已知点A,且半径为2 cm
B
探索新知
2
知识点
圆心角、扇形
·
圆心角:我们把顶点在圆心的角叫做圆心角.
O
B
A
∠AOB为圆心角
圆心角∠AOB所对的弦为AB,所对的弧为AB.
⌒
探索新知
判别下列各图中的角是不是圆心角,并说明理由.
①
②
③
④
探索新知
任意给圆心角,对应出现三个量:
圆心角
弧
弦
·
O
B
A
疑问:这三个量之间会有什么关系呢?
探索新知
归 纳
(1)1°的圆心角所对的弧叫做1°的弧.这样,n°的圆心角所对的弧就是n°的弧.
(2)圆心角的度数与它所对的弧的度数是一致(或相等)的,即圆心角的度数等于它所对弧的度数.注意这里仅指度数相等.
探索新知
例2 下面四个图形中的角,是圆心角的是( )
D
探索新知
扇形:由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形.
探索新知
例3 将一个圆分割成三个扇形,它们的圆心角的度
数比为1 : 2 : 3,求这三个扇形的圆心角的度数.
解:因为一个周角为360°,所以分成的三个扇形的圆心角分别是:
探索新知
总 结
圆可以分割成若干个扇形.①扇形的面积比等于各扇形的圆心角的度数比.②扇形的面积公式为S扇形= (扇形圆心角的度数为n°,半径为r,S扇形表示扇形的面积).
典题精讲
下列说法正确的是( )
A.扇形是由弧、线段围成的多边形
B.弧是半圆
C.半圆是弧
D.过圆心的线段是直径
1
C
典题精讲
如图,已知AB是圆O的直径,点C,D是弧BE上的三等分点,∠AOE=60°,则∠COE是( )
A.40°
B.60°
C.80°
D.120°
2
C
学以致用
小试牛刀
1 .将一个圆分成四个扇形A、B、C、D,它们的面积之比为2:3:3:4,则最大扇形的圆心角为 度
120°
2.把一个圆分成四个扇形,四个扇形面积分别占圆面积的10%,20%,30%,40%,则这四个扇形的圆心角分别为_____________________________.
36°,72°,108°,144°
3.如图,甲、乙、丙三个扇形圆心角的度数分别为_______________________.
90°,108°,162°
小试牛刀
4.下列说法正确的是( )
A.由不在同一直线上的几条线段相连所组成的封闭图形叫做多边形
B.一条弧和经过弧的两条半径围成的图形叫做扇形
C.三角形是最简单的多边形
D.圆的一部分是扇形
C
小试牛刀
5 .如图所示,阴影部分扇形的圆心角是( )
A.45° B.43° C.50° D.54°
6 .如图所示,在一个圆中任意画3条半径,可以把这个圆分成几个扇形( )
A.3 B.4 C.5 D.6
D
D
小试牛刀
7.如图,把一个圆分成四个扇形,请分别求出这四个扇形的圆心角的度数.若该圆的半径为2 cm,请分别求出它们的面积.
解:
扇形OAB的圆心角为360°×35%=126°,
扇形OBC的圆心角为360°×10%=36°,
扇形OCD的圆心角为360°×25%=90°,
小试牛刀
扇形OAD的圆心角为360°×30%=108°.
因为圆的面积为π×22=4π(cm2),
所以S扇形OAB=4π×35%=1.4π(cm2),
S扇形OBC=4π×10%=0.4π(cm2),
S扇形OCD=4π×25%=π(cm2),
S扇形OAD=4π×30%=1.2π(cm2).
小试牛刀
8.从下午2时15分到下午5时30分,时钟的时针转了多少度?
解:
由题意知,时针走的大格数为3.5-0.25.
因此时针转的角度为30°×(3.5-0.25)=97.5°.
故从下午2时15分到下午5时30分,
时钟的时针转了97.5°.
小试牛刀
9.如图,正方形的边长为a,以各边为直径在正方形内作半圆,求图中阴影部分的面积.
小试牛刀
10 .将如图所示的一个圆分割成四个扇形,
它们的圆心角的度数比为2∶3∶4∶3.
(1) 求这四个扇形的圆心角的度数,并画出这四个扇形;
(2) 若圆的半径为2 cm,请求出这四个扇形的面积.
解:(1)60°,90°,120°,90° 画图略
课堂小结
课堂小结
2.圆上A、B两点之间的部分叫做弧,由一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形。
3. 圆可以分割成若干个扇形。
1.平面上,一条线段绕着它固定的一个端点旋转一周,另一个端点形成的图形叫做圆。固定的端点称为圆心,线段称为半径。
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
4.5 多边形和圆的初步认识
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
圆是常见的图形,生活中的许多物体都给我们以圆的形象(如图).
新课精讲
探索新知
1
知识点
圆及相关概念
上面的图形中有我们熟悉的圆和扇形,你还记得用哪些方法可以画一个圆吗?你能用一根细绳和笔画出一个圆吗?
做一做
探索新知
圆的定义: 在一个平面内,线段OA饶它的一个端点O旋转一周,另一个端点A随之旋转所形成的的图形叫做圆. 固定的端点O叫做圆心,线段OA叫做半径.
如图:以O为圆心的圆,记作“⊙O”,读作“圆O”
探索新知
由圆的定义可知:
(1)圆上的各点到定点(圆心O)的距离等于定长(半径的长r );
(2)到定点的距离等于定长的点都在圆上.
因此,圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点的集合.
r
O
A
探索新知
O
A
点A是圆上的点
OA是圆的半径
B
C
D
连接圆上任意两点的线段(如图中的线段BC、BD)叫做弦.
经过圆心的弦(如图中的BD)叫做直径.
探索新知
半径和直径的特点:
半径有( )条,
直径有( )条,
直径是半径的( ),
半径是直径的( ).
无数
无数
2倍
在同一个(等)圆内,
探索新知
弧:圆上任意两点间的部分叫做圆弧,简称弧.如图,以A、B
为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
半圆:圆的任意一条直径的两个端点把圆分成两条弧,每一条弧
都叫做半圆.
⌒
·
C
O
A
B
探索新知
·
C
O
A
B
圆心O
直径AB
弦AC
优弧ABC,记作
劣弧AC,记作
O′
半径OO′
探索新知
以下命题:(1)半圆是弧,但弧不一定是半圆;(2)过圆上任意一点只能作一条弦,且这条弦是直径;(3)弦是直径;(4)直径是圆中最长的弦;(5)直径不是弦;(6)优弧大于劣弧;(7)以O为圆心可以画无数个圆. 正确的个数为( )
A.1 B.2 C.3 D.4
C
例1
探索新知
(1)半圆是弧的一种,弧可以分为劣弧、半圆、优 弧三种,故正确;(2)过圆上任意一点可以作无数条弦,故错误;(3)直径是过圆心的特殊弦,但弦不一定是直径,故错误;(4)圆有无数条弦,过圆心的弦最长,即直径是圆中最长的弦,故正确;(5)直径是圆中最长的弦,故错误;(6)在同圆或等 圆中,优弧大于劣弧,故错误;(7)以一个点为圆 心,若不指明半径,可画出无数个大小不等的同心圆,故正确.
导引:
典题精讲
平面上,一条线段绕着它固定的一个端点旋转一周,另一个端点形成的图形叫做________.固定的端点称为________,这条线段称为________.圆上任意两点间的部分叫做________,简称________.
圆
圆心
半径
圆弧
弧
2 下列条件中,能确定圆的是( )
A.以已知点O为圆心
B.以点O为圆心,2 cm为半径
C.以2 cm为半径
D.经过已知点A,且半径为2 cm
B
探索新知
2
知识点
圆心角、扇形
·
圆心角:我们把顶点在圆心的角叫做圆心角.
O
B
A
∠AOB为圆心角
圆心角∠AOB所对的弦为AB,所对的弧为AB.
⌒
探索新知
判别下列各图中的角是不是圆心角,并说明理由.
①
②
③
④
探索新知
任意给圆心角,对应出现三个量:
圆心角
弧
弦
·
O
B
A
疑问:这三个量之间会有什么关系呢?
探索新知
归 纳
(1)1°的圆心角所对的弧叫做1°的弧.这样,n°的圆心角所对的弧就是n°的弧.
(2)圆心角的度数与它所对的弧的度数是一致(或相等)的,即圆心角的度数等于它所对弧的度数.注意这里仅指度数相等.
探索新知
例2 下面四个图形中的角,是圆心角的是( )
D
探索新知
扇形:由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形.
探索新知
例3 将一个圆分割成三个扇形,它们的圆心角的度
数比为1 : 2 : 3,求这三个扇形的圆心角的度数.
解:因为一个周角为360°,所以分成的三个扇形的圆心角分别是:
探索新知
总 结
圆可以分割成若干个扇形.①扇形的面积比等于各扇形的圆心角的度数比.②扇形的面积公式为S扇形= (扇形圆心角的度数为n°,半径为r,S扇形表示扇形的面积).
典题精讲
下列说法正确的是( )
A.扇形是由弧、线段围成的多边形
B.弧是半圆
C.半圆是弧
D.过圆心的线段是直径
1
C
典题精讲
如图,已知AB是圆O的直径,点C,D是弧BE上的三等分点,∠AOE=60°,则∠COE是( )
A.40°
B.60°
C.80°
D.120°
2
C
学以致用
小试牛刀
1 .将一个圆分成四个扇形A、B、C、D,它们的面积之比为2:3:3:4,则最大扇形的圆心角为 度
120°
2.把一个圆分成四个扇形,四个扇形面积分别占圆面积的10%,20%,30%,40%,则这四个扇形的圆心角分别为_____________________________.
36°,72°,108°,144°
3.如图,甲、乙、丙三个扇形圆心角的度数分别为_______________________.
90°,108°,162°
小试牛刀
4.下列说法正确的是( )
A.由不在同一直线上的几条线段相连所组成的封闭图形叫做多边形
B.一条弧和经过弧的两条半径围成的图形叫做扇形
C.三角形是最简单的多边形
D.圆的一部分是扇形
C
小试牛刀
5 .如图所示,阴影部分扇形的圆心角是( )
A.45° B.43° C.50° D.54°
6 .如图所示,在一个圆中任意画3条半径,可以把这个圆分成几个扇形( )
A.3 B.4 C.5 D.6
D
D
小试牛刀
7.如图,把一个圆分成四个扇形,请分别求出这四个扇形的圆心角的度数.若该圆的半径为2 cm,请分别求出它们的面积.
解:
扇形OAB的圆心角为360°×35%=126°,
扇形OBC的圆心角为360°×10%=36°,
扇形OCD的圆心角为360°×25%=90°,
小试牛刀
扇形OAD的圆心角为360°×30%=108°.
因为圆的面积为π×22=4π(cm2),
所以S扇形OAB=4π×35%=1.4π(cm2),
S扇形OBC=4π×10%=0.4π(cm2),
S扇形OCD=4π×25%=π(cm2),
S扇形OAD=4π×30%=1.2π(cm2).
小试牛刀
8.从下午2时15分到下午5时30分,时钟的时针转了多少度?
解:
由题意知,时针走的大格数为3.5-0.25.
因此时针转的角度为30°×(3.5-0.25)=97.5°.
故从下午2时15分到下午5时30分,
时钟的时针转了97.5°.
小试牛刀
9.如图,正方形的边长为a,以各边为直径在正方形内作半圆,求图中阴影部分的面积.
小试牛刀
10 .将如图所示的一个圆分割成四个扇形,
它们的圆心角的度数比为2∶3∶4∶3.
(1) 求这四个扇形的圆心角的度数,并画出这四个扇形;
(2) 若圆的半径为2 cm,请求出这四个扇形的面积.
解:(1)60°,90°,120°,90° 画图略
课堂小结
课堂小结
2.圆上A、B两点之间的部分叫做弧,由一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形。
3. 圆可以分割成若干个扇形。
1.平面上,一条线段绕着它固定的一个端点旋转一周,另一个端点形成的图形叫做圆。固定的端点称为圆心,线段称为半径。
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
