北师大版(新)八上-3.2 平面直角坐标系 第二课时【优质课件】
文档属性
| 名称 | 北师大版(新)八上-3.2 平面直角坐标系 第二课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 7.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:52:29 | ||
图片预览








文档简介
(共29张PPT)
3.2 平面直角坐标系
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1.什么是平面直角坐标系?
2.象限内点的坐标有什么特征?
复
习
回
顾
新课精讲
探索新知
1
知识点
坐标轴及象限角平分线上的点的坐标特征
例 在直角坐标系中描出下列各点,并将各组内这些点依次用线段连接.
(1)D(-3,5), E(-7, 3), C(l,3), D(-3,5);
(2)F(-6,3), G(-6,0), A(0,0), B(0,3);
观察所描出的图形,它像什么?根据图形回答下列问题:
(1)图形中哪些点在坐标轴上,它们的坐标有什么特点?
(2)线段EC与x轴有什么位置关系?点E和点C的坐标有什么特点?线段EC上其他点的坐标呢?
(3)点F和点G的横坐标有什么共同特点?线段FG与y轴有怎样的位置关系?
探索新知
解:连接起来的图形像“房子”(如图).
(1)线段AG上的点都在x轴
上,它们的纵坐标都等
于0;线段AB上的点、
线段CD与y轴的交点,
它们都在y轴上,它们的横坐标都等于0.
(2)线段EC平行于x轴,点E和点C的纵坐标相同.线
段EC上其他点的纵坐标也相同,都是3.
(3)点F和点G的横坐标相同,线段FG与y轴平行.
探索新知
议一议
在平面直角坐标系中,坐标轴上的点的坐标有什么特点?
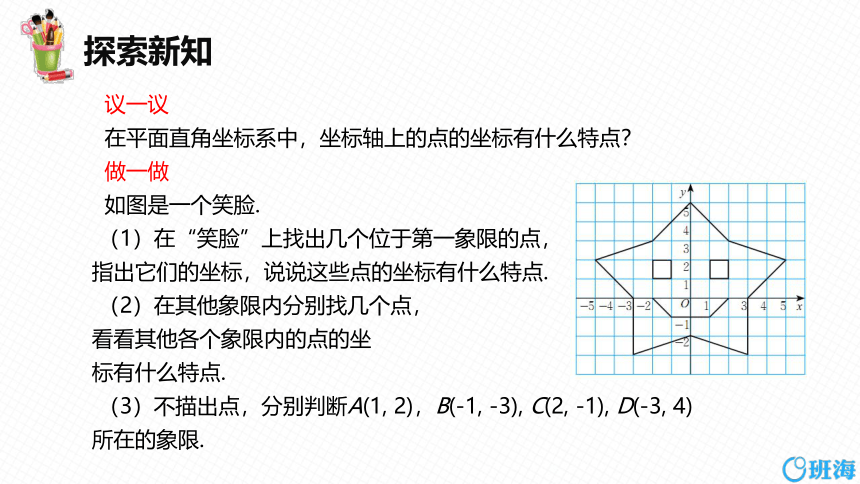
做一做
如图是一个笑脸.
(1)在“笑脸”上找出几个位于第一象限的点,
指出它们的坐标,说说这些点的坐标有什么特点.
(2)在其他象限内分别找几个点,
看看其他各个象限内的点的坐
标有什么特点.
(3)不描出点,分别判断A(1, 2),B(-1, -3), C(2, -1), D(-3, 4)所在的象限.
探索新知
1.象限内点的特征:
点M(x,y)所处的位置 坐标特征
象限内 的点 点M在第一象限 M(正,正)
点M在第二象限 M(负,正)
点M在第三象限 M(负,负)
点M在第四象限 M(正,负)
探索新知
2.特殊位置的点的特征:
点M(x,y)所处的位置 坐标特征
坐标轴上的点 点M在x轴上 在x轴正半轴上:M(正,0)
在x轴负半轴上:M(负,0)
点M在y轴上 在y轴正半轴上:M(0,正)
在y轴负半轴上:M(0,负)
象限角平分线上的点 点M在第一、三象限角平分线上 x=y,即横坐标
与纵坐标相等
点M在第二、四象限角平分线上 x=-y,即横、纵坐
标互为相反数
(1)
探索新知
(2)①平行于x轴的直线上的点的纵坐标相等;平行于y轴的直线上的点的横坐标相等.
②关于x轴对称的点,横坐标相等,纵坐标互为相反数;关于y轴对称的点,横坐标互为相反数,纵坐标相等.
探索新知
【例1】已知点P(x+6,x-4)在y轴上,则点P的坐标是__________.
导引:根据y 轴上点的坐标的特征可得x+6=0,得x=-6,所以x-4=-10.故点P的坐标是(0,-10).
(0,-10)
典题精讲
1 点P(m+1,m+3)在x轴上,则点P的坐标是( )
A.(-2,0) B.(4,0)
C.(2,0) D.(0,-4)
2 若点P(m,1-2m)的横坐标与纵坐标互为相反数,则点P 一定在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3 若点A(-2,n)在x轴上,则点B(n-2,n+1)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
A
A
D
探索新知
2
知识点
平行于两坐标轴的直线上的点的坐标特征
【例2】如图,长方形ABCD的长与宽分别是6,4,建立适当的直角坐标系,并写出各个顶点的坐标.
解:以点C为坐标原点,分别以CD,CB所在直线为x轴、y轴,建立直角坐标系,如图.此时点C的坐标是(0,0).由CD=6,CB=4,可得D,B,A的坐标分别为D(6,0),B(0,4), A(6,4).
议一议:在例2中,你还可以怎样建立直角坐标系?与同伴进行交流.
探索新知
【例3】对于边长为4的等边三角形ABC (如图),建立适当的直角坐标系,写出各个顶点的坐标.
解:如图,以边BC所在直线为x轴,以边BC的中垂线为y轴建立直角坐标系.由等边三角形的性质可知顶点A,B,C的坐标分别为
B(-2,0),C(2,0).
探索新知
议一议
在一次“寻宝”游戏中,寻宝人已经找到了A(3, 2)和B(3,-2)两个标志点(如图),并且知道藏宝地点的坐标为(4, 4),除此之外不知道其他信息.如何确定直角坐标系找到“宝藏”?与同伴进行交流.
典题精讲
1 如图,长方形ABCD的边CD在y轴上,点O为CD的中点.已知AB=4,AB交x轴于点E(-5,0),则点B的坐标为( )
A.(-5,2) B.(2,5)
C.(5,-2) D.(-5,-2)
D
学以致用
小试牛刀
1.如图,在平面直角坐标系中,l1,l2分别为第一、三和二、四象限的角平分线.点A,B,C,D的位置如图所示,则表示这些点的坐标分别为:A____________;B____________;C____________;D____________.
(2,2)
(-2,2)
(-1,0)
(0,-1)
2.已知点P(2m-5,m-1).
(1)当m=______时,点P在第二、四象限的角平分线上;
(2)当m=______时,点P在第一、三象限的角平分线上.
2
4
小试牛刀
3.在平面直角坐标系内,平行于x轴(垂直于y轴)的直线上的点的纵坐标________;平行于y轴(垂直于x轴)的直线上的点的横坐标________.
相等
相等
4.已知点M(1,-2),N(-3,-2),则直线MN与x轴、y轴的位置关系分别为________、________.
5.已知点A(2,n),B(m,-4)不重合.
(1)若线段AB∥x轴,且点A,B到y轴距离相等,则m=________,n=________;
(2)若线段AB∥y轴,且点A,B到x轴距离相等,则m=________,n=________.
平行
垂直
-2
-4
2
4
小试牛刀
6.在平面直角坐标系中,点Q(0,-m2-2)一定在( )
A.第一象限 B.第四象限
C.x轴上 D.y轴上
7.已知点P(0,m)在y轴的负半轴上,则点M(-m,-m+1)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D
A
小试牛刀
8.已知点A(0,3),B(-1,1),C(-3,2),D(-2,0),
E(-3,-2),F(-1,-1),G(0,-3),H(1,-1),
I(3,-2),J(2,0),K(3,2),L(1,1).
(1)请在如图所示的平面直角坐标系中,分别描出上述各点,并顺次连接;
解:
(1)如图所示.
小试牛刀
(2)试求(1)中连线围成的图形的面积.
(2)第一象限中的图形与坐标轴围成的图形面积为
因为图形被坐标轴平均分成四部分,
所以图形的总面积为4×4=16.
小试牛刀
9.已知点P(3m-6,m+1),试分别根据下列条件,求出点P的坐标:
(1)点P在y轴上;
解:(1)因为点P(3m-6,m+1)在y轴上,
所以3m-6=0,解得m=2.
所以m+1=2+1=3.
所以点P的坐标为(0,3).
小试牛刀
(2)点P在x轴上;
(2)因为点P(3m-6,m+1)在x轴上,所以m+1=0,
解得m=-1.
所以3m-6=3×(-1)-6=-9.
所以点P的坐标为(-9,0).
(3)点P的纵坐标比横坐标大5;
(3)因为点P(3m-6,m+1)的纵坐标比横坐标大5,
所以m+1-(3m-6)=5,解得m=1.
所以3m-6=3×1-6=-3,m+1=1+1=2.
所以点P的坐标为(-3,2).
小试牛刀
(4)因为点P(3m-6,m+1)在过点A(-1,2)且与x轴平行的直线上,
所以m+1=2,解得m=1.
所以3m-6=3×1-6=-3.
所以点P的坐标为(-3,2).
(4)点P在过点A(-1,2)且与x轴平行的直线上.
课堂小结
课堂小结
特殊条件下点的坐标的特征:
1.平行于x 轴的直线上的点的纵坐标相等;平行于y轴的直线上的点的横坐标相等.
2.关于x轴对称的点,横坐标相等,纵坐标互为相反数;关于y轴对称的点,横坐标互为相反数,纵坐标相等.
3.第一、三象限内坐标轴夹角平分线上的点,横坐标与纵坐标相等;第二、四象限内坐标轴夹角平分线上的点,横坐标与纵坐标互为相反数.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
3.2 平面直角坐标系
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1.什么是平面直角坐标系?
2.象限内点的坐标有什么特征?
复
习
回
顾
新课精讲
探索新知
1
知识点
坐标轴及象限角平分线上的点的坐标特征
例 在直角坐标系中描出下列各点,并将各组内这些点依次用线段连接.
(1)D(-3,5), E(-7, 3), C(l,3), D(-3,5);
(2)F(-6,3), G(-6,0), A(0,0), B(0,3);
观察所描出的图形,它像什么?根据图形回答下列问题:
(1)图形中哪些点在坐标轴上,它们的坐标有什么特点?
(2)线段EC与x轴有什么位置关系?点E和点C的坐标有什么特点?线段EC上其他点的坐标呢?
(3)点F和点G的横坐标有什么共同特点?线段FG与y轴有怎样的位置关系?
探索新知
解:连接起来的图形像“房子”(如图).
(1)线段AG上的点都在x轴
上,它们的纵坐标都等
于0;线段AB上的点、
线段CD与y轴的交点,
它们都在y轴上,它们的横坐标都等于0.
(2)线段EC平行于x轴,点E和点C的纵坐标相同.线
段EC上其他点的纵坐标也相同,都是3.
(3)点F和点G的横坐标相同,线段FG与y轴平行.
探索新知
议一议
在平面直角坐标系中,坐标轴上的点的坐标有什么特点?
做一做
如图是一个笑脸.
(1)在“笑脸”上找出几个位于第一象限的点,
指出它们的坐标,说说这些点的坐标有什么特点.
(2)在其他象限内分别找几个点,
看看其他各个象限内的点的坐
标有什么特点.
(3)不描出点,分别判断A(1, 2),B(-1, -3), C(2, -1), D(-3, 4)所在的象限.
探索新知
1.象限内点的特征:
点M(x,y)所处的位置 坐标特征
象限内 的点 点M在第一象限 M(正,正)
点M在第二象限 M(负,正)
点M在第三象限 M(负,负)
点M在第四象限 M(正,负)
探索新知
2.特殊位置的点的特征:
点M(x,y)所处的位置 坐标特征
坐标轴上的点 点M在x轴上 在x轴正半轴上:M(正,0)
在x轴负半轴上:M(负,0)
点M在y轴上 在y轴正半轴上:M(0,正)
在y轴负半轴上:M(0,负)
象限角平分线上的点 点M在第一、三象限角平分线上 x=y,即横坐标
与纵坐标相等
点M在第二、四象限角平分线上 x=-y,即横、纵坐
标互为相反数
(1)
探索新知
(2)①平行于x轴的直线上的点的纵坐标相等;平行于y轴的直线上的点的横坐标相等.
②关于x轴对称的点,横坐标相等,纵坐标互为相反数;关于y轴对称的点,横坐标互为相反数,纵坐标相等.
探索新知
【例1】已知点P(x+6,x-4)在y轴上,则点P的坐标是__________.
导引:根据y 轴上点的坐标的特征可得x+6=0,得x=-6,所以x-4=-10.故点P的坐标是(0,-10).
(0,-10)
典题精讲
1 点P(m+1,m+3)在x轴上,则点P的坐标是( )
A.(-2,0) B.(4,0)
C.(2,0) D.(0,-4)
2 若点P(m,1-2m)的横坐标与纵坐标互为相反数,则点P 一定在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3 若点A(-2,n)在x轴上,则点B(n-2,n+1)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
A
A
D
探索新知
2
知识点
平行于两坐标轴的直线上的点的坐标特征
【例2】如图,长方形ABCD的长与宽分别是6,4,建立适当的直角坐标系,并写出各个顶点的坐标.
解:以点C为坐标原点,分别以CD,CB所在直线为x轴、y轴,建立直角坐标系,如图.此时点C的坐标是(0,0).由CD=6,CB=4,可得D,B,A的坐标分别为D(6,0),B(0,4), A(6,4).
议一议:在例2中,你还可以怎样建立直角坐标系?与同伴进行交流.
探索新知
【例3】对于边长为4的等边三角形ABC (如图),建立适当的直角坐标系,写出各个顶点的坐标.
解:如图,以边BC所在直线为x轴,以边BC的中垂线为y轴建立直角坐标系.由等边三角形的性质可知顶点A,B,C的坐标分别为
B(-2,0),C(2,0).
探索新知
议一议
在一次“寻宝”游戏中,寻宝人已经找到了A(3, 2)和B(3,-2)两个标志点(如图),并且知道藏宝地点的坐标为(4, 4),除此之外不知道其他信息.如何确定直角坐标系找到“宝藏”?与同伴进行交流.
典题精讲
1 如图,长方形ABCD的边CD在y轴上,点O为CD的中点.已知AB=4,AB交x轴于点E(-5,0),则点B的坐标为( )
A.(-5,2) B.(2,5)
C.(5,-2) D.(-5,-2)
D
学以致用
小试牛刀
1.如图,在平面直角坐标系中,l1,l2分别为第一、三和二、四象限的角平分线.点A,B,C,D的位置如图所示,则表示这些点的坐标分别为:A____________;B____________;C____________;D____________.
(2,2)
(-2,2)
(-1,0)
(0,-1)
2.已知点P(2m-5,m-1).
(1)当m=______时,点P在第二、四象限的角平分线上;
(2)当m=______时,点P在第一、三象限的角平分线上.
2
4
小试牛刀
3.在平面直角坐标系内,平行于x轴(垂直于y轴)的直线上的点的纵坐标________;平行于y轴(垂直于x轴)的直线上的点的横坐标________.
相等
相等
4.已知点M(1,-2),N(-3,-2),则直线MN与x轴、y轴的位置关系分别为________、________.
5.已知点A(2,n),B(m,-4)不重合.
(1)若线段AB∥x轴,且点A,B到y轴距离相等,则m=________,n=________;
(2)若线段AB∥y轴,且点A,B到x轴距离相等,则m=________,n=________.
平行
垂直
-2
-4
2
4
小试牛刀
6.在平面直角坐标系中,点Q(0,-m2-2)一定在( )
A.第一象限 B.第四象限
C.x轴上 D.y轴上
7.已知点P(0,m)在y轴的负半轴上,则点M(-m,-m+1)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D
A
小试牛刀
8.已知点A(0,3),B(-1,1),C(-3,2),D(-2,0),
E(-3,-2),F(-1,-1),G(0,-3),H(1,-1),
I(3,-2),J(2,0),K(3,2),L(1,1).
(1)请在如图所示的平面直角坐标系中,分别描出上述各点,并顺次连接;
解:
(1)如图所示.
小试牛刀
(2)试求(1)中连线围成的图形的面积.
(2)第一象限中的图形与坐标轴围成的图形面积为
因为图形被坐标轴平均分成四部分,
所以图形的总面积为4×4=16.
小试牛刀
9.已知点P(3m-6,m+1),试分别根据下列条件,求出点P的坐标:
(1)点P在y轴上;
解:(1)因为点P(3m-6,m+1)在y轴上,
所以3m-6=0,解得m=2.
所以m+1=2+1=3.
所以点P的坐标为(0,3).
小试牛刀
(2)点P在x轴上;
(2)因为点P(3m-6,m+1)在x轴上,所以m+1=0,
解得m=-1.
所以3m-6=3×(-1)-6=-9.
所以点P的坐标为(-9,0).
(3)点P的纵坐标比横坐标大5;
(3)因为点P(3m-6,m+1)的纵坐标比横坐标大5,
所以m+1-(3m-6)=5,解得m=1.
所以3m-6=3×1-6=-3,m+1=1+1=2.
所以点P的坐标为(-3,2).
小试牛刀
(4)因为点P(3m-6,m+1)在过点A(-1,2)且与x轴平行的直线上,
所以m+1=2,解得m=1.
所以3m-6=3×1-6=-3.
所以点P的坐标为(-3,2).
(4)点P在过点A(-1,2)且与x轴平行的直线上.
课堂小结
课堂小结
特殊条件下点的坐标的特征:
1.平行于x 轴的直线上的点的纵坐标相等;平行于y轴的直线上的点的横坐标相等.
2.关于x轴对称的点,横坐标相等,纵坐标互为相反数;关于y轴对称的点,横坐标互为相反数,纵坐标相等.
3.第一、三象限内坐标轴夹角平分线上的点,横坐标与纵坐标相等;第二、四象限内坐标轴夹角平分线上的点,横坐标与纵坐标互为相反数.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
