北师大版(新)八上-3.2 平面直角坐标系 第三课时【优质课件】
文档属性
| 名称 | 北师大版(新)八上-3.2 平面直角坐标系 第三课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:52:29 | ||
图片预览








文档简介
(共31张PPT)
3.2 平面直角坐标系
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
在如图所示的平面直角坐标系中,第一、二象限内各有一面小旗.
(1)两面小旗之间有怎样的位置关系?对应点A与A1的坐标又有什么共同特点?其他对应的点也有这个特点吗?
(2)在这个坐标系里画出小旗ABCD关于x轴的对称图形, 它的各个“顶点”的坐标与原来的点的坐标有什么关系?
新课精讲
探索新知
1
知识点
关于x轴对称的两个点的坐标特征
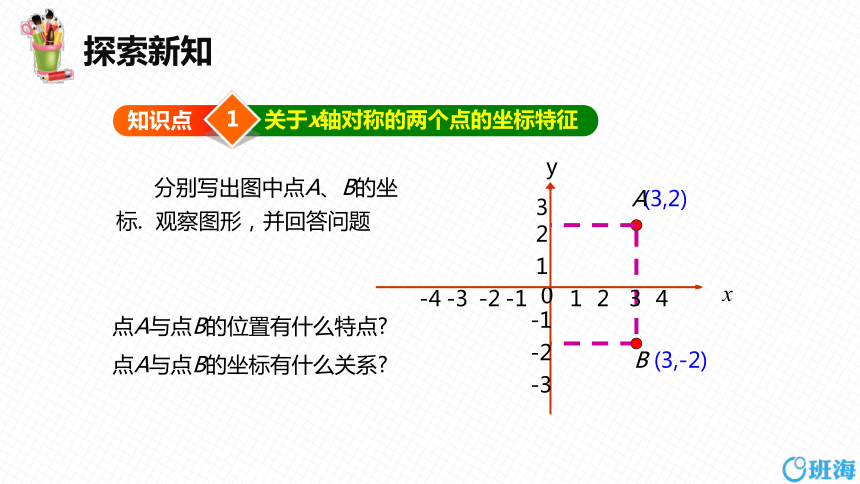
分别写出图中点A、B的坐标. 观察图形,并回答问题
(3,2)
(3,-2)
-2
-1
4
3
2
1
-3
-4
y
1
2
3
-3
-1
-2
0
点A与点B的位置有什么特点
点A与点B的坐标有什么关系
A
B
探索新知
关于x轴对称点的坐标的特征:
(1) 横坐标相同,纵坐标互为相反数.
(2)用坐标表示轴对称的性质:
点P(x,y)关于x轴对称的点的坐标为(x,-y);
探索新知
(1)在平面直角坐标系中依次连接下列各点:
(0, 0), (5, 4),(3, 0), (5, 1), (5, -1), (3, 0), (4, -2), (0, 0), 你得到了一个怎样的图案?
(2)将所得图案的各个“顶点”的纵坐标保持不变,横坐标分别乘-1,依次连接这些点, 你会得到怎样的图案?这个图案与原图案又有怎样的位置关系呢?
探索新知
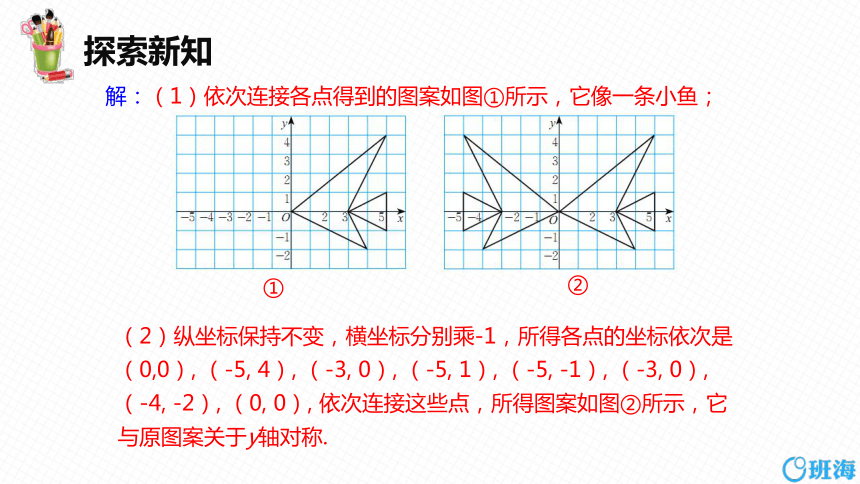
解:(1)依次连接各点得到的图案如图①所示,它像一条小鱼;
(2)纵坐标保持不变,横坐标分别乘-1,所得各点的坐标依次是(0,0), (-5, 4), (-3, 0), (-5, 1), (-5, -1), (-3, 0), (-4, -2), (0, 0), 依次连接这些点,所得图案如图②所示,它与原图案关于y轴对称.
①
②
典题精讲
在平面直角坐标系中,点P(-2,3) 关于x轴对称的点的坐标为( )
A.(-2,-3) B.(2,-3)
C.(-3,-2) D.(3,-2)
1
A
探索新知
2
知识点
关于y轴对称的两个点的坐标特征
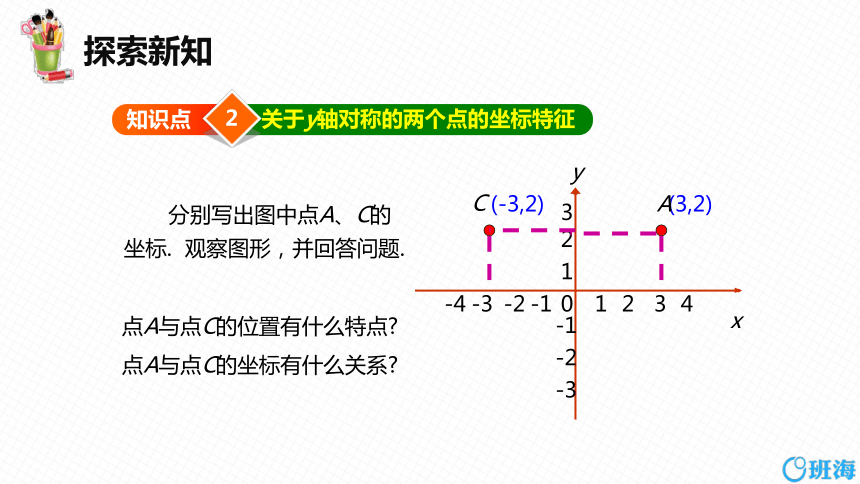
分别写出图中点A、C的坐标. 观察图形,并回答问题.
(3,2)
-2
-1
4
3
2
1
-3
-4
y
1
2
3
-3
-1
-2
(-3,2)
0
点A与点C的位置有什么特点
点A与点C的坐标有什么关系
A
C
x
探索新知
关于y轴对称点的坐标的特征:
(1) 纵坐标相同,横坐标互为相反数.
(2)用坐标表示轴对称的性质:
点P(x,y)关于y轴对称的点的坐标为(-x,y).
①上述性质可简称为:横对称,横不变,纵相反;纵对称,纵不变,横相反.
②关于坐标轴对称的点的坐标只有符号不同,其绝对值相同.
探索新知
例2 已知点A(m+2,3),B(-5,n+6)关于y轴对称,则m=____,n=_____.
导引:由关于y轴对称的点的坐标特征得m+2=5,n+6=3,
解得m=3,n=-3.
3
-3
探索新知
总 结
本题运用了方程思想,根据题意列出方程是解题的关键.关于x轴对称的点的坐标特征是纵坐标互为相反数,横坐标相等;关于y轴对称的点的坐标特征是横坐标互为相反数,纵坐标相等.
探索新知
例3 如图,在平面直角坐标系中,已知点A(0,3),B(2,4),C(4,0),D(2,-3),E(0,-4).写出B,C,D关于y轴对称的点H,G,F的坐标,并画出H,G,F点.顺次平滑地连接A,B,C,D,E,F,G,H,A各点.
导引:方法一:点(x,y)关于y轴对称的点的坐标是(-x,y),作点B,C,D关于y轴对称的点的关键是确定各对称点的坐标,然后顺次平滑连接各点即得所要求的图形;方法二:利用轴对称先作出图形,再直观判断F,G,H的坐标.
探索新知
解:方法一:点B,C,D关于y轴对称的点的坐标分别为H(-2,4),G(-4,0),F(-2,-3),根据坐标描出点H,G,F,并顺次平滑地连接A,B,C,D,E,F,G,H,A各点即得所求图形,如图所示.
方法二:先作出点B,C,D关于y轴的对称点H,G,F,观察得出H(-2,4),G(-4,0),F(-2,-3),再顺次平滑地连接A,B,C,D,E,F,G,H,A各点即得所求图形,如图所示.
探索新知
总 结
在直角坐标系中作关于坐标轴对称的图形的方法有两种:一是首先找到已知图形的各关键点,然后根据轴对称的特征确定各关键点关于坐标轴的对称点的坐标,描点、顺次连接各点即可;二是按照一般情况,先作出特殊点关于坐标轴的对称点,再顺次连接对称点即可.
典题精讲
如图,△ABC与△DFE关于y轴对称,已知A(-4,6),B(-6,2),E(2,1),则点D的坐标为( )
A.(-6,4)
B.(4,6)
C.(-2,1)
D.(6,2)
1
B
典题精讲
将一个图形各点的横坐标分别乘-1,纵坐标不变,所得的图形与原图形的关系是( )
A.关于x轴对称
B.关于y轴对称
C.关于第一、三象限的平分线对称
D.无法确定
2
B
学以致用
小试牛刀
1.构建几何图形中坐标系的方法:
(1)以某已知点为原点;
(2)以图形中某条线段所在的直线为____轴(或____轴);
(3)以线段的中点为原点;
(4)以两条直线的交点为原点.
x
y
小试牛刀
2.利用平面直角坐标系绘制区域内一些地点分布情况平面图的过程如下:
(1)建立坐标系,选择一个适当的参照点为______,确定x轴、y轴的正方向;
(2)根据具体问题确定__________;
原点
单位长度
(3)在坐标平面内画出这些点,写出各点的________和各个地点的________.
坐标
名称
小试牛刀
3.如图,正方形ABCD的边长为4,请以它的两条对称轴为两坐标轴,建立平面直角坐标系,则点A,B,C,D的坐标分别是___________,___________,___________,___________.
(-2,-2)
(2,-2)
(2,2)
(-2,2)
小试牛刀
4.如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(-3,2),(b,m),(c,m),则点E的坐标是( )
A.(2,-3) B.(2,3)
C.(3,2) D.(3,-2)
C
5.如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1,3),则点C的坐标为( )
A.(-3,1) B.(-1,3)
C.(3,1) D.(-3,-1)
A
小试牛刀
6.如图,将北京市地铁部分铁路图置于正方形网格中,若设定崇文门站的坐标为(0,-1),雍和宫站的坐标为(0,4),则西单站的坐标为( )
A.(0,5) B.(5,0)
C.(0,-5) D.(-5,0)
D
小试牛刀
7.如图是利用网格画出的太原市地铁1,2,3号线路部分规划示意图.若建立适当的平面直角坐标系,表示双塔西街的点的坐标为(0,-1),表示桃园路的点的坐标为(-1,0),则表示太原火车站的点(正好在网格点上)的坐标是________.
(3,0)
小试牛刀
8.如图,已知四边形ABCD(网格中每个小正方形的边长均为1).
(1)写出点A,B,C,D的坐标;
(2)试求四边形ABCD的面积.
解:
(1)A(-2,1),B(-3,-2),C(3,-2),D(1,2).
(2)S四边形ABCD=3×3+2× ×1×3+ ×2×4=16.
小试牛刀
9.图中标明了李明家附近的一些地方.
(1)写出学校和邮局的坐标;
(2)某星期日早晨,李明从家里出发,沿(-1,2),(1,0),
(2,1),(2,-2),(-1,-2),(0,-1)的路线转了一下,又回到家里,请依次写出他在路上经过的地方.
解:(1)由题图可知:学校的坐标为(1,3),邮局的坐标为(-3,-1).
(2)李明在路上依次经过的地方是糖果店、汽车站、游乐场、消防站、宠物店、姥姥家.
课堂小结
课堂小结
用坐标表示轴对称的性质:
(1)点P(x,y)关于x轴对称的点的坐标为 (x,-y);
(2)点P(x,y)关于y轴对称的点的坐标为(-x,y).
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
3.2 平面直角坐标系
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
在如图所示的平面直角坐标系中,第一、二象限内各有一面小旗.
(1)两面小旗之间有怎样的位置关系?对应点A与A1的坐标又有什么共同特点?其他对应的点也有这个特点吗?
(2)在这个坐标系里画出小旗ABCD关于x轴的对称图形, 它的各个“顶点”的坐标与原来的点的坐标有什么关系?
新课精讲
探索新知
1
知识点
关于x轴对称的两个点的坐标特征
分别写出图中点A、B的坐标. 观察图形,并回答问题
(3,2)
(3,-2)
-2
-1
4
3
2
1
-3
-4
y
1
2
3
-3
-1
-2
0
点A与点B的位置有什么特点
点A与点B的坐标有什么关系
A
B
探索新知
关于x轴对称点的坐标的特征:
(1) 横坐标相同,纵坐标互为相反数.
(2)用坐标表示轴对称的性质:
点P(x,y)关于x轴对称的点的坐标为(x,-y);
探索新知
(1)在平面直角坐标系中依次连接下列各点:
(0, 0), (5, 4),(3, 0), (5, 1), (5, -1), (3, 0), (4, -2), (0, 0), 你得到了一个怎样的图案?
(2)将所得图案的各个“顶点”的纵坐标保持不变,横坐标分别乘-1,依次连接这些点, 你会得到怎样的图案?这个图案与原图案又有怎样的位置关系呢?
探索新知
解:(1)依次连接各点得到的图案如图①所示,它像一条小鱼;
(2)纵坐标保持不变,横坐标分别乘-1,所得各点的坐标依次是(0,0), (-5, 4), (-3, 0), (-5, 1), (-5, -1), (-3, 0), (-4, -2), (0, 0), 依次连接这些点,所得图案如图②所示,它与原图案关于y轴对称.
①
②
典题精讲
在平面直角坐标系中,点P(-2,3) 关于x轴对称的点的坐标为( )
A.(-2,-3) B.(2,-3)
C.(-3,-2) D.(3,-2)
1
A
探索新知
2
知识点
关于y轴对称的两个点的坐标特征
分别写出图中点A、C的坐标. 观察图形,并回答问题.
(3,2)
-2
-1
4
3
2
1
-3
-4
y
1
2
3
-3
-1
-2
(-3,2)
0
点A与点C的位置有什么特点
点A与点C的坐标有什么关系
A
C
x
探索新知
关于y轴对称点的坐标的特征:
(1) 纵坐标相同,横坐标互为相反数.
(2)用坐标表示轴对称的性质:
点P(x,y)关于y轴对称的点的坐标为(-x,y).
①上述性质可简称为:横对称,横不变,纵相反;纵对称,纵不变,横相反.
②关于坐标轴对称的点的坐标只有符号不同,其绝对值相同.
探索新知
例2 已知点A(m+2,3),B(-5,n+6)关于y轴对称,则m=____,n=_____.
导引:由关于y轴对称的点的坐标特征得m+2=5,n+6=3,
解得m=3,n=-3.
3
-3
探索新知
总 结
本题运用了方程思想,根据题意列出方程是解题的关键.关于x轴对称的点的坐标特征是纵坐标互为相反数,横坐标相等;关于y轴对称的点的坐标特征是横坐标互为相反数,纵坐标相等.
探索新知
例3 如图,在平面直角坐标系中,已知点A(0,3),B(2,4),C(4,0),D(2,-3),E(0,-4).写出B,C,D关于y轴对称的点H,G,F的坐标,并画出H,G,F点.顺次平滑地连接A,B,C,D,E,F,G,H,A各点.
导引:方法一:点(x,y)关于y轴对称的点的坐标是(-x,y),作点B,C,D关于y轴对称的点的关键是确定各对称点的坐标,然后顺次平滑连接各点即得所要求的图形;方法二:利用轴对称先作出图形,再直观判断F,G,H的坐标.
探索新知
解:方法一:点B,C,D关于y轴对称的点的坐标分别为H(-2,4),G(-4,0),F(-2,-3),根据坐标描出点H,G,F,并顺次平滑地连接A,B,C,D,E,F,G,H,A各点即得所求图形,如图所示.
方法二:先作出点B,C,D关于y轴的对称点H,G,F,观察得出H(-2,4),G(-4,0),F(-2,-3),再顺次平滑地连接A,B,C,D,E,F,G,H,A各点即得所求图形,如图所示.
探索新知
总 结
在直角坐标系中作关于坐标轴对称的图形的方法有两种:一是首先找到已知图形的各关键点,然后根据轴对称的特征确定各关键点关于坐标轴的对称点的坐标,描点、顺次连接各点即可;二是按照一般情况,先作出特殊点关于坐标轴的对称点,再顺次连接对称点即可.
典题精讲
如图,△ABC与△DFE关于y轴对称,已知A(-4,6),B(-6,2),E(2,1),则点D的坐标为( )
A.(-6,4)
B.(4,6)
C.(-2,1)
D.(6,2)
1
B
典题精讲
将一个图形各点的横坐标分别乘-1,纵坐标不变,所得的图形与原图形的关系是( )
A.关于x轴对称
B.关于y轴对称
C.关于第一、三象限的平分线对称
D.无法确定
2
B
学以致用
小试牛刀
1.构建几何图形中坐标系的方法:
(1)以某已知点为原点;
(2)以图形中某条线段所在的直线为____轴(或____轴);
(3)以线段的中点为原点;
(4)以两条直线的交点为原点.
x
y
小试牛刀
2.利用平面直角坐标系绘制区域内一些地点分布情况平面图的过程如下:
(1)建立坐标系,选择一个适当的参照点为______,确定x轴、y轴的正方向;
(2)根据具体问题确定__________;
原点
单位长度
(3)在坐标平面内画出这些点,写出各点的________和各个地点的________.
坐标
名称
小试牛刀
3.如图,正方形ABCD的边长为4,请以它的两条对称轴为两坐标轴,建立平面直角坐标系,则点A,B,C,D的坐标分别是___________,___________,___________,___________.
(-2,-2)
(2,-2)
(2,2)
(-2,2)
小试牛刀
4.如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(-3,2),(b,m),(c,m),则点E的坐标是( )
A.(2,-3) B.(2,3)
C.(3,2) D.(3,-2)
C
5.如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1,3),则点C的坐标为( )
A.(-3,1) B.(-1,3)
C.(3,1) D.(-3,-1)
A
小试牛刀
6.如图,将北京市地铁部分铁路图置于正方形网格中,若设定崇文门站的坐标为(0,-1),雍和宫站的坐标为(0,4),则西单站的坐标为( )
A.(0,5) B.(5,0)
C.(0,-5) D.(-5,0)
D
小试牛刀
7.如图是利用网格画出的太原市地铁1,2,3号线路部分规划示意图.若建立适当的平面直角坐标系,表示双塔西街的点的坐标为(0,-1),表示桃园路的点的坐标为(-1,0),则表示太原火车站的点(正好在网格点上)的坐标是________.
(3,0)
小试牛刀
8.如图,已知四边形ABCD(网格中每个小正方形的边长均为1).
(1)写出点A,B,C,D的坐标;
(2)试求四边形ABCD的面积.
解:
(1)A(-2,1),B(-3,-2),C(3,-2),D(1,2).
(2)S四边形ABCD=3×3+2× ×1×3+ ×2×4=16.
小试牛刀
9.图中标明了李明家附近的一些地方.
(1)写出学校和邮局的坐标;
(2)某星期日早晨,李明从家里出发,沿(-1,2),(1,0),
(2,1),(2,-2),(-1,-2),(0,-1)的路线转了一下,又回到家里,请依次写出他在路上经过的地方.
解:(1)由题图可知:学校的坐标为(1,3),邮局的坐标为(-3,-1).
(2)李明在路上依次经过的地方是糖果店、汽车站、游乐场、消防站、宠物店、姥姥家.
课堂小结
课堂小结
用坐标表示轴对称的性质:
(1)点P(x,y)关于x轴对称的点的坐标为 (x,-y);
(2)点P(x,y)关于y轴对称的点的坐标为(-x,y).
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
