北师大版(新)八上-4.4 一次函数的应用 第二课时【优质课件】
文档属性
| 名称 | 北师大版(新)八上-4.4 一次函数的应用 第二课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 8.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:52:29 | ||
图片预览










文档简介
(共33张PPT)
4.4 一次函数的应用
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
回顾旧知
一次函数的表达式为:
2. 正比例函数的表达式为:
y=kx+b (k, b为常数,k≠0)
y=kx(k为常数,k≠0)
3. 直线y=3x+1与直线y=3x-2有什么样的位置关系?
平行
新课精讲
探索新知
1
知识点
一次函数的实际应用
1.利用函数方法解决实际问题,关键是分析题中的数量关系,联系实际生活及以前学过的内容,将实际问题抽象、升华为一次函数模型,即建模,再利用函数的性质解决问题.一次函数的应用主要有两种类型:(1)给出了一次函数关系式,直接应用一次函数的性质解决问题;
(2)只用语言叙述或用表格、图象提供一次函数的情境时,应先求出关系式,进而利用函数性质解决问题.
探索新知
2.要点精析:“建模”可以把实际问题转化为关于一次函数的数学问题,它的关键是确定函数与自变量之间的关系式,并确定实际问题中自变量的取值范围.
探索新知
例1 某种摩托车的油箱加满油后,油箱中的剩余油量y(L)与摩托车行驶路程x ( km )之间的关系如图所示.根据图象回答下列问题:
(1)油箱最多可储油多少升?
(2)一箱汽油可供摩托车行驶多少千米?
(3)摩托车每行驶100 km消耗多少升汽油?
(4)油箱中的剩余油量小于1 L时,摩托车将
自动报警.行驶多少千米后,摩托车将自动报警?
探索新知
解:观察图象,得
(1)当x = 0时,y=10.因此,油箱最多可储油10L.
(2)当y = 0时,x = 500.因此,一箱汽油可供摩托车行
驶500 km.
(3) x从0增加到100时,y从10减少到8,减少了 2,因此
摩托车每行驶100 km消耗2 L汽油.
当y=1时, x= 450.因此,行驶450km后,摩托车将自动报警.
典题精讲
1
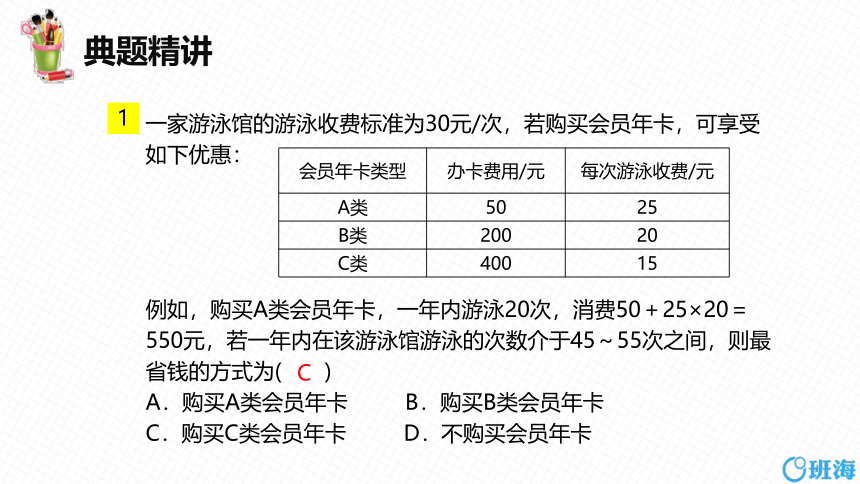
一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:
例如,购买A类会员年卡,一年内游泳20次,消费50+25×20=550元,若一年内在该游泳馆游泳的次数介于45~55次之间,则最省钱的方式为( )
A.购买A类会员年卡 B.购买B类会员年卡
C.购买C类会员年卡 D.不购买会员年卡
会员年卡类型 办卡费用/元 每次游泳收费/元
A类 50 25
B类 200 20
C类 400 15
C
典题精讲
2
今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(min),所走的路程为s(m),s与t之间的函数关系如图所示.下列说法错误的是( )
A.小明中途休息了20 min
B.小明休息前爬山的平均速度为70 m/min
C.小明在上述过程中所走的路程为6 600 m
D.小明休息前爬山的平均速度大于休息后
爬山的平均速度
C
探索新知
2
知识点
一次函数与一元一次方程的关系
做一做
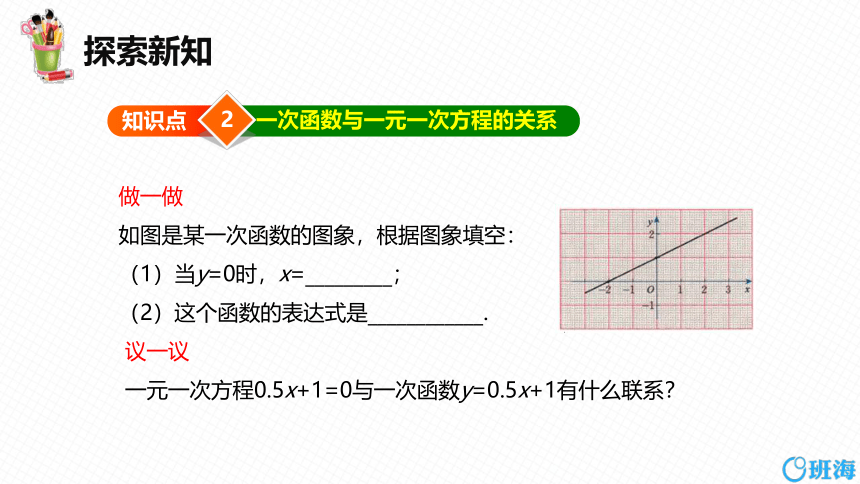
如图是某一次函数的图象,根据图象填空:
(1)当y=0时,x=_________;
(2)这个函数的表达式是____________.
议一议
一元一次方程0.5x+1=0与一次函数y=0.5x+1有什么联系?
探索新知
1.一次函数和一元一次方程的联系:任何一个以x为未知数的一元一次方程都可以变形为ax+b=0(a≠0,a,b为常数)的形式,所以解一元一次方程可以转化为:求一次函数y=ax+b(a≠0,a,b为常数)的函数值为0时,自变量x的取值;反映在图象上,就是直线y=ax+b与x轴交点的横坐标.
2.利用一次函数图象解一元一次方程的步骤:
(1)转化:将一元一次方程转化为一次函数;
(2)画图象:画出一次函数的图象;
(3)找交点:找出一次函数图象与x轴的交点,得到其横坐标,即为一元一次方程的解.
探索新知
例2 一个冷冻室开始的温度是12 ℃,开机降温后室温每小
时下降6 ℃,设T(℃)表示开机降温t h时的温度.
(1)写出T(℃)与t(h)之间的函数关系式,并画出其图象.
(2)利用图象说明:经过几小时,冷冻室温度降至0 ℃?何时降至-9 ℃?
导引:(1)由题意,t h室温下降6t ℃,所以T=12-6t,显然T与t之间是一次函数关系,可用描点法在直角坐标系内画出其图象,但要注意t≥0;(2)是要求方程12-6t=0和12-6t=-9的解,观察(1)中所画的图象即可求出.
探索新知
知识点
解:(1)依题意,得T与t之间的函数关系式为T=12-6t(t≥0),用描点法画出图象,如图所示.
(2)观察图象发现,方程12-6t=0的解是T=12-6t(t≥0)的图象
与t 轴交点的横坐标,所以解是t=2,表明经过2 h,冷冻室
温度降至0 ℃;方程12-6t=-9的解是
直线T=12-6t与直线T=-9交点的
横坐标,为3.5,即它的解为t=3.5,
表明经过3.5 h,冷冻室温度降至-9 ℃.
探索新知
总 结
(1)用图象法求解此题,运用的是数形结合思想;
(2)题的实质是已知函数图象上一点的纵坐标,求相应的横坐标.
典题精讲
1
已知一次函数y=2x+n的图象如图所示,则方程2x+n=0的解是( )
A.x=1
B.x=
C.x=-
D.x=-1
C
典题精讲
2
甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:km),甲行驶的时间为t(单位:h),s与t之间的函数关
系如图所示,有下列结论:
①出发1 h时,甲、乙在途中相遇;
②出发1.5 h时,乙比甲多行驶了60 km;
③出发3 h时,甲、乙同时到达终点;
④甲的速度是乙速度的一半.
其中,正确结论的个数是( )
A.4 B.3 C.2 D.1
B
学以致用
小试牛刀
1.一辆汽车由A地开往B地,它距离B地的路程s(km)与行驶时间t(h)的关系如图所示,如果汽车一直快速行驶,那么可以提前___小时到达B地.
解析:320-160=160千米,
160÷2=80千米/小时.
320÷80=4小时.
6-4=2.
故答案为:2.
2
小试牛刀
2.甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的 距离y(km)与甲车行驶的时间t(h)之间的函数关系如图所示,则下列结论:
①A,B两城相距300 km;
②乙车比甲车晚出发1 h,却早到1 h;
③乙车出发后2.5 h追上甲车;
④当甲、乙两车相距50 km时,t= 或 .
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
B
小试牛刀
3.一旅游团来到某旅游景点,看到售票处旁边的公告栏如下图所示,请根据公告栏内容回答下列问题:
(1)若旅游团人数为9人,门票费用是多少?若旅游团人数为30人,门票费用又是多少?
(2)设旅游团人数为人,写出该旅游团门票费用(元)与人数的关系式.
解:(1)180×9=1620(元) 180×10+180×60%×(30-10)=3960(元);
答:若旅游团人数为9人,门票费用是1620元,若人数为30人,门票费用是3960元.
(2)
小试牛刀
某商场计划投入一笔资金采购一批紧俏商品,经市场调研发现,如果本月初出售,可获利10%,然后将本利再投资其他商品,到下月初又可获利10%;如果下月初出售可获利25%,但要支付仓储费8 000元.设商场投入资金x元,请你根据商场的资金情况,向商场提出合理化建议,说明何时出售获利较多.
4.
小试牛刀
设如果商场本月初出售,下月初可获利y1元,
则y1=10%x+(1+10%)x 10%
=0.1x+0.11x=0.21x.
设如果商场下月初出售,可获利y2元,
则y2=25%x-8 000=0.25x-8 000.
当y1=y2时,0.21x=0.25x-8 000,
解得x=200 000.
所以若商场投入资金为20万元,两种出售方式获利相同;若商场投入资金少于20万元,本月初出售获利较多;若商场投入资金多于20万元,下月初出售获利较多.
解:
小试牛刀
某教育行政部门计划今年暑假组织部分教师到外地进行学习,预订宾馆住宿时,有住宿条件一样的甲、乙两家宾馆供选择,其收费标准均为每人每天120元,并且各自推出不同的优惠方案.甲家是35人(含35人)以内的按标准收费,超过35人的,超出部分按九折收费;乙家是45人(含45人)以内的按标准收费,超过45人的,超出部分按八折收费.如果你是这个部门的负责人,你认为选择哪家宾馆更实惠些?
5.
小试牛刀
设总人数是x人,甲、乙宾馆的收费分别
为y甲,y乙.
当x≤35时,选择两家宾馆是一样的;
当35当x>45时,y甲=35×120+0.9×120×(x-35),
即y甲=108x+420,
y乙=45×120+0.8×120×(x-45)
=96x+1 080.
当y甲=y乙时,可得x=55;
当y甲>y乙时,可得x>55;
解:
小试牛刀
当y甲综上可得,当x≤35或x=55时,
选择两家宾馆是一样的;
当35当x>55时,选择乙宾馆比较实惠.
小试牛刀
甲、乙两地相距300 km,一辆货车和一辆轿车先后从甲地出发驶向乙地.如图,线段OA表示货车离甲地的距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系,根据图象,解答下列问题:
(1)线段CD表示轿车在途中停留了________;
(2)求线段DE对应的函数表达式;
(3)求轿车从甲地出发后经过多长时间追上货车.
0.5 h
6.
小试牛刀
(2)设线段DE对应的函数表达式为y=kx+b
(2.5≤x≤4.5).将D(2.5,80),E(4.5,300)的坐标分别代入y=kx+b可得,80=2.5k+b,300=4.5k+b.解得k=110,b=-195.所以y=110x-195(2.5≤x≤4.5).
解:
小试牛刀
(3)设线段OA对应的函数表达式为y=k1x(0≤x≤5).
将A(5,300)的坐标代入y=k1x,
可得300=5k1,解得k1=60.
所以y=60x(0≤x≤5).
令60x=110x-195,解得x=3.9.
故轿车从甲地出发后经过3.9-1=2.9(h)追上货车.
课堂小结
课堂小结
任何一元一次方程都可以转化为ax+b=0(a,b为常数,a≠0)的形式,所以解一元一次方程可以转化为当某个一次函数的函数值为0时,求相应的自变量的值.从图象上看,相当于已知直线y=ax+b,确定它与x轴的交点的横坐标.即“形”题用“数”解,“数”题用“形”解,充分体现了数形结合的思想.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
4.4 一次函数的应用
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
回顾旧知
一次函数的表达式为:
2. 正比例函数的表达式为:
y=kx+b (k, b为常数,k≠0)
y=kx(k为常数,k≠0)
3. 直线y=3x+1与直线y=3x-2有什么样的位置关系?
平行
新课精讲
探索新知
1
知识点
一次函数的实际应用
1.利用函数方法解决实际问题,关键是分析题中的数量关系,联系实际生活及以前学过的内容,将实际问题抽象、升华为一次函数模型,即建模,再利用函数的性质解决问题.一次函数的应用主要有两种类型:(1)给出了一次函数关系式,直接应用一次函数的性质解决问题;
(2)只用语言叙述或用表格、图象提供一次函数的情境时,应先求出关系式,进而利用函数性质解决问题.
探索新知
2.要点精析:“建模”可以把实际问题转化为关于一次函数的数学问题,它的关键是确定函数与自变量之间的关系式,并确定实际问题中自变量的取值范围.
探索新知
例1 某种摩托车的油箱加满油后,油箱中的剩余油量y(L)与摩托车行驶路程x ( km )之间的关系如图所示.根据图象回答下列问题:
(1)油箱最多可储油多少升?
(2)一箱汽油可供摩托车行驶多少千米?
(3)摩托车每行驶100 km消耗多少升汽油?
(4)油箱中的剩余油量小于1 L时,摩托车将
自动报警.行驶多少千米后,摩托车将自动报警?
探索新知
解:观察图象,得
(1)当x = 0时,y=10.因此,油箱最多可储油10L.
(2)当y = 0时,x = 500.因此,一箱汽油可供摩托车行
驶500 km.
(3) x从0增加到100时,y从10减少到8,减少了 2,因此
摩托车每行驶100 km消耗2 L汽油.
当y=1时, x= 450.因此,行驶450km后,摩托车将自动报警.
典题精讲
1
一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:
例如,购买A类会员年卡,一年内游泳20次,消费50+25×20=550元,若一年内在该游泳馆游泳的次数介于45~55次之间,则最省钱的方式为( )
A.购买A类会员年卡 B.购买B类会员年卡
C.购买C类会员年卡 D.不购买会员年卡
会员年卡类型 办卡费用/元 每次游泳收费/元
A类 50 25
B类 200 20
C类 400 15
C
典题精讲
2
今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(min),所走的路程为s(m),s与t之间的函数关系如图所示.下列说法错误的是( )
A.小明中途休息了20 min
B.小明休息前爬山的平均速度为70 m/min
C.小明在上述过程中所走的路程为6 600 m
D.小明休息前爬山的平均速度大于休息后
爬山的平均速度
C
探索新知
2
知识点
一次函数与一元一次方程的关系
做一做
如图是某一次函数的图象,根据图象填空:
(1)当y=0时,x=_________;
(2)这个函数的表达式是____________.
议一议
一元一次方程0.5x+1=0与一次函数y=0.5x+1有什么联系?
探索新知
1.一次函数和一元一次方程的联系:任何一个以x为未知数的一元一次方程都可以变形为ax+b=0(a≠0,a,b为常数)的形式,所以解一元一次方程可以转化为:求一次函数y=ax+b(a≠0,a,b为常数)的函数值为0时,自变量x的取值;反映在图象上,就是直线y=ax+b与x轴交点的横坐标.
2.利用一次函数图象解一元一次方程的步骤:
(1)转化:将一元一次方程转化为一次函数;
(2)画图象:画出一次函数的图象;
(3)找交点:找出一次函数图象与x轴的交点,得到其横坐标,即为一元一次方程的解.
探索新知
例2 一个冷冻室开始的温度是12 ℃,开机降温后室温每小
时下降6 ℃,设T(℃)表示开机降温t h时的温度.
(1)写出T(℃)与t(h)之间的函数关系式,并画出其图象.
(2)利用图象说明:经过几小时,冷冻室温度降至0 ℃?何时降至-9 ℃?
导引:(1)由题意,t h室温下降6t ℃,所以T=12-6t,显然T与t之间是一次函数关系,可用描点法在直角坐标系内画出其图象,但要注意t≥0;(2)是要求方程12-6t=0和12-6t=-9的解,观察(1)中所画的图象即可求出.
探索新知
知识点
解:(1)依题意,得T与t之间的函数关系式为T=12-6t(t≥0),用描点法画出图象,如图所示.
(2)观察图象发现,方程12-6t=0的解是T=12-6t(t≥0)的图象
与t 轴交点的横坐标,所以解是t=2,表明经过2 h,冷冻室
温度降至0 ℃;方程12-6t=-9的解是
直线T=12-6t与直线T=-9交点的
横坐标,为3.5,即它的解为t=3.5,
表明经过3.5 h,冷冻室温度降至-9 ℃.
探索新知
总 结
(1)用图象法求解此题,运用的是数形结合思想;
(2)题的实质是已知函数图象上一点的纵坐标,求相应的横坐标.
典题精讲
1
已知一次函数y=2x+n的图象如图所示,则方程2x+n=0的解是( )
A.x=1
B.x=
C.x=-
D.x=-1
C
典题精讲
2
甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:km),甲行驶的时间为t(单位:h),s与t之间的函数关
系如图所示,有下列结论:
①出发1 h时,甲、乙在途中相遇;
②出发1.5 h时,乙比甲多行驶了60 km;
③出发3 h时,甲、乙同时到达终点;
④甲的速度是乙速度的一半.
其中,正确结论的个数是( )
A.4 B.3 C.2 D.1
B
学以致用
小试牛刀
1.一辆汽车由A地开往B地,它距离B地的路程s(km)与行驶时间t(h)的关系如图所示,如果汽车一直快速行驶,那么可以提前___小时到达B地.
解析:320-160=160千米,
160÷2=80千米/小时.
320÷80=4小时.
6-4=2.
故答案为:2.
2
小试牛刀
2.甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的 距离y(km)与甲车行驶的时间t(h)之间的函数关系如图所示,则下列结论:
①A,B两城相距300 km;
②乙车比甲车晚出发1 h,却早到1 h;
③乙车出发后2.5 h追上甲车;
④当甲、乙两车相距50 km时,t= 或 .
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
B
小试牛刀
3.一旅游团来到某旅游景点,看到售票处旁边的公告栏如下图所示,请根据公告栏内容回答下列问题:
(1)若旅游团人数为9人,门票费用是多少?若旅游团人数为30人,门票费用又是多少?
(2)设旅游团人数为人,写出该旅游团门票费用(元)与人数的关系式.
解:(1)180×9=1620(元) 180×10+180×60%×(30-10)=3960(元);
答:若旅游团人数为9人,门票费用是1620元,若人数为30人,门票费用是3960元.
(2)
小试牛刀
某商场计划投入一笔资金采购一批紧俏商品,经市场调研发现,如果本月初出售,可获利10%,然后将本利再投资其他商品,到下月初又可获利10%;如果下月初出售可获利25%,但要支付仓储费8 000元.设商场投入资金x元,请你根据商场的资金情况,向商场提出合理化建议,说明何时出售获利较多.
4.
小试牛刀
设如果商场本月初出售,下月初可获利y1元,
则y1=10%x+(1+10%)x 10%
=0.1x+0.11x=0.21x.
设如果商场下月初出售,可获利y2元,
则y2=25%x-8 000=0.25x-8 000.
当y1=y2时,0.21x=0.25x-8 000,
解得x=200 000.
所以若商场投入资金为20万元,两种出售方式获利相同;若商场投入资金少于20万元,本月初出售获利较多;若商场投入资金多于20万元,下月初出售获利较多.
解:
小试牛刀
某教育行政部门计划今年暑假组织部分教师到外地进行学习,预订宾馆住宿时,有住宿条件一样的甲、乙两家宾馆供选择,其收费标准均为每人每天120元,并且各自推出不同的优惠方案.甲家是35人(含35人)以内的按标准收费,超过35人的,超出部分按九折收费;乙家是45人(含45人)以内的按标准收费,超过45人的,超出部分按八折收费.如果你是这个部门的负责人,你认为选择哪家宾馆更实惠些?
5.
小试牛刀
设总人数是x人,甲、乙宾馆的收费分别
为y甲,y乙.
当x≤35时,选择两家宾馆是一样的;
当35
即y甲=108x+420,
y乙=45×120+0.8×120×(x-45)
=96x+1 080.
当y甲=y乙时,可得x=55;
当y甲>y乙时,可得x>55;
解:
小试牛刀
当y甲
选择两家宾馆是一样的;
当35
小试牛刀
甲、乙两地相距300 km,一辆货车和一辆轿车先后从甲地出发驶向乙地.如图,线段OA表示货车离甲地的距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系,根据图象,解答下列问题:
(1)线段CD表示轿车在途中停留了________;
(2)求线段DE对应的函数表达式;
(3)求轿车从甲地出发后经过多长时间追上货车.
0.5 h
6.
小试牛刀
(2)设线段DE对应的函数表达式为y=kx+b
(2.5≤x≤4.5).将D(2.5,80),E(4.5,300)的坐标分别代入y=kx+b可得,80=2.5k+b,300=4.5k+b.解得k=110,b=-195.所以y=110x-195(2.5≤x≤4.5).
解:
小试牛刀
(3)设线段OA对应的函数表达式为y=k1x(0≤x≤5).
将A(5,300)的坐标代入y=k1x,
可得300=5k1,解得k1=60.
所以y=60x(0≤x≤5).
令60x=110x-195,解得x=3.9.
故轿车从甲地出发后经过3.9-1=2.9(h)追上货车.
课堂小结
课堂小结
任何一元一次方程都可以转化为ax+b=0(a,b为常数,a≠0)的形式,所以解一元一次方程可以转化为当某个一次函数的函数值为0时,求相应的自变量的值.从图象上看,相当于已知直线y=ax+b,确定它与x轴的交点的横坐标.即“形”题用“数”解,“数”题用“形”解,充分体现了数形结合的思想.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
