北师大版(新)八上-4.4 一次函数的应用 第三课时【优质课件】
文档属性
| 名称 | 北师大版(新)八上-4.4 一次函数的应用 第三课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:52:29 | ||
图片预览








文档简介
(共36张PPT)
4.4 一次函数的应用
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
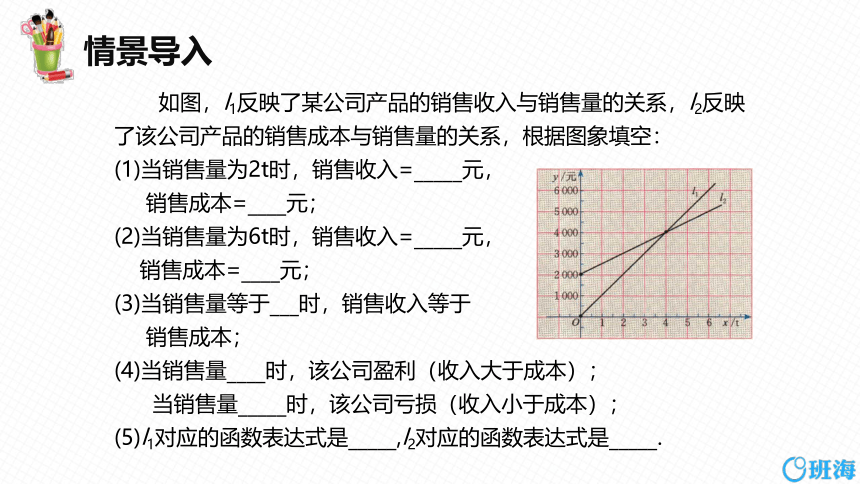
如图,l1反映了某公司产品的销售收入与销售量的关系,l2反映
了该公司产品的销售成本与销售量的关系,根据图象填空:
(1)当销售量为2t时,销售收入=_____元,
销售成本=____元;
(2)当销售量为6t时,销售收入=_____元,
销售成本=____元;
(3)当销售量等于___时,销售收入等于
销售成本;
(4)当销售量____时,该公司盈利(收入大于成本);
当销售量_____时,该公司亏损(收入小于成本);
(5)l1对应的函数表达式是_____,l2对应的函数表达式是_____.
情景导入
想一想
图中,l1对应的一次函数y=k1x+b1中,k1和b1的实际意义各是什么?l2对应的一次函数y=k2x+b2中,k2和b2的实际意义各是什么?
答:k1的实际意义是:每销售1t产品的销售收入;
b1的实际意义是:未销售时,销售收入为0;
k2的实际意义是:每销售1t的销售成本;
b2的实际意义是:未销售时,为销售所花的成本为2000元.
新课精讲
探索新知
1
知识点
从图表中获取信息的应用
公司有330台机器需要一次性运送到某地,计划租用甲、乙两种货车共8辆,已知每辆甲种货车一次最多运送机器45台,租车费用为400元,每辆乙种货车一次最多运送机器30台,租车费用为280元.
例1
探索新知
315
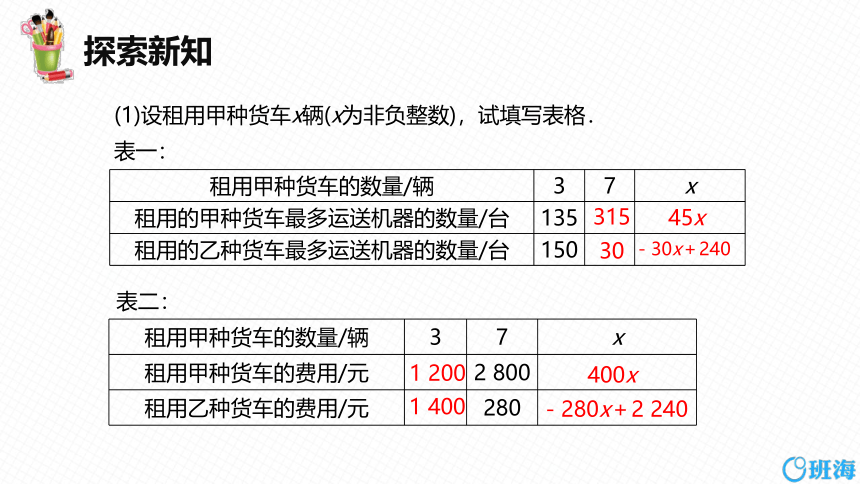
(1)设租用甲种货车x辆(x为非负整数),试填写表格.
表一:
租用甲种货车的数量/辆 3 7 x
租用的甲种货车最多运送机器的数量/台 135
租用的乙种货车最多运送机器的数量/台 150
表二:
租用甲种货车的数量/辆 3 7 x
租用甲种货车的费用/元 2 800
租用乙种货车的费用/元 280
45x
30
-30x+240
1 200
400x
1 400
-280x+2 240
探索新知
能完成此项运送任务的最节省费用的租车方案是
甲种货车6辆,乙种货车2辆.
理由:当租用甲种货车x辆时,
设两种货车的总费用为y元,
则两种货车的总费用
y=400x+(-280x+2 240)=120x+2 240.
解:
(2)给出能完成此项运送任务的最节省费用的租车方
案,并说明理由.
探索新知
又因为45x+(-30x+240)≥330,
所以x≥6. 因为120>0,
所以在函数y=120x+2 240中,y随x的增大而增大.
所以当x=6时,y取得最小值.
即能完成此项运送任务的最节省费用的租车方案是
甲种货车6辆,乙种货车2辆.
典题精讲
1
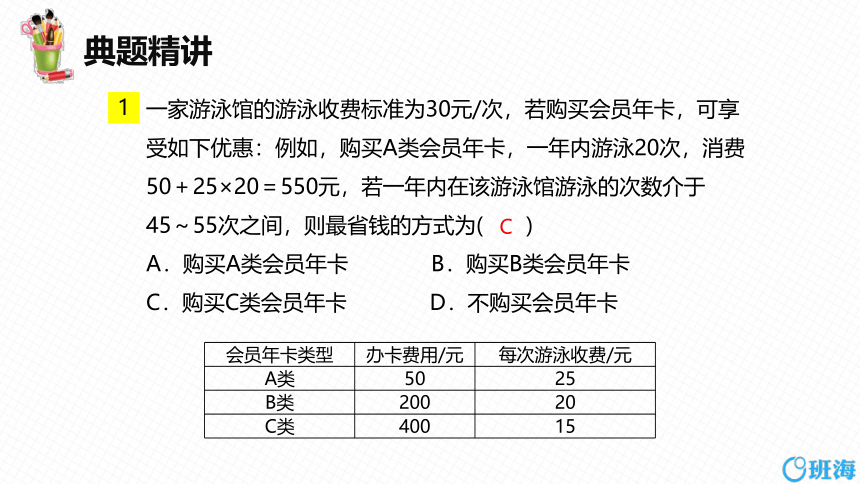
一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:例如,购买A类会员年卡,一年内游泳20次,消费50+25×20=550元,若一年内在该游泳馆游泳的次数介于45~55次之间,则最省钱的方式为( )
A.购买A类会员年卡 B.购买B类会员年卡
C.购买C类会员年卡 D.不购买会员年卡
会员年卡类型 办卡费用/元 每次游泳收费/元
A类 50 25
B类 200 20
C类 400 15
C
探索新知
2
知识点
从函数图象中获取信息的应用
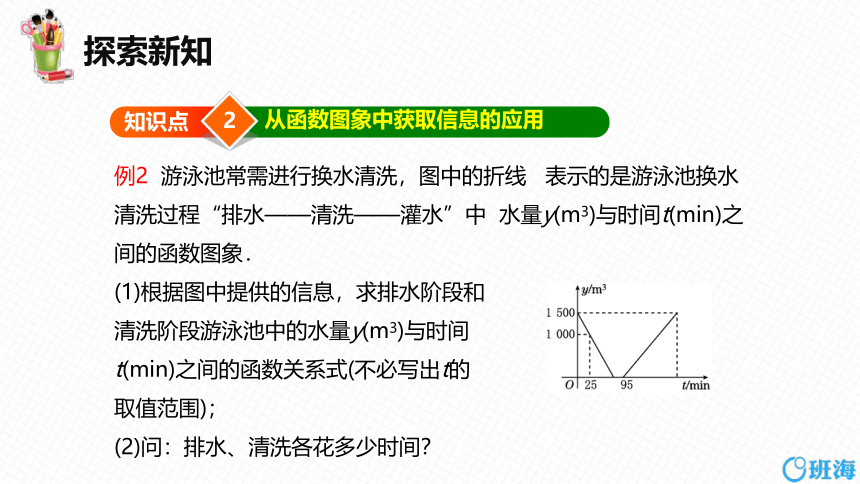
例2 游泳池常需进行换水清洗,图中的折线 表示的是游泳池换水清洗过程“排水——清洗——灌水”中 水量y(m3)与时间t(min)之间的函数图象.
(1)根据图中提供的信息,求排水阶段和
清洗阶段游泳池中的水量y(m3)与时间
t(min)之间的函数关系式(不必写出t的
取值范围);
(2)问:排水、清洗各花多少时间?
探索新知
导引:(1)根据图象上点的坐标利用待定系数法求得排水阶段的函数关系式,显然清洗阶段的函数 关系式为y=0;
(2)根据(1)中所求函数关系式,可得出函数图象与x轴的交点坐标,即可得出答案.
探索新知
知识点
解:(1)排水阶段:设y与t之间的函数关系式为y=kt+b,
因为图象经过点(0,1 500),(25,1 000),
所以b=1 500,25k+b=1 000,解得k=-20.
故排水阶段y与t之间的函数关系式为y=-20t+1 500;
清洗阶段y与t之间的函数关系式为y=0.
(2)因为排水阶段y与t之间的函数关系式为y=-20t+1 500,
所以y=0时,0=-20t+1 500,解得t=75.
故排水时间为75 min,清洗时间为95-75=20(min).
探索新知
总 结
此题主要考查了用待定系数法求一次函数的关系式及函数图象与x轴交点坐标的求法,根据图象得出正确的信息是解题关键.
探索新知
知识点
例3 手机上网已经成为当今年轻人时尚的网络生活,某网络公司看中了这种商机,推出了两种手机上网的计费方式:方式A以每分钟0.1元的价格按上网时间计费;方式B除收月租费20元外,再以每分钟0.06元的价格按上网时间计费.假设某客户月上网时间为x min,上网费用为y元.
(1)分别写出该客户按A,B两种方式的上网费用
y(元)与每月上网时间x(min)的函数关系式,
并在图所示的坐标系中画出这两个函数的图象;
(2)如何选择计费方式能使该客户上网费用更合算?
探索新知
知识点
导引:(1)根据题意可直接写出A,B两种上网方式的上网费用y(元)与每月上网时间x(min)的函数关系式,再分别取x的一些特殊值,如0,500,算出对应的y值,根据一次函数的图象是一条直线,分别过求得的两点画直线即可画出这两个函数的图象;(2)根据题意并观察图象可得到不同上网时间范围内选择何种计费方式上网更合算.
解:(1)设方式A:yA=k1x,方式B:yB=k2x+b.
由题意易求得yA=0.1x,yB=0.06x+20,
当x=0时,yA=0,yB=20;
当x=500时,yA=50,yB=50,
探索新知
所以一次函数yA=0.1x的图象过点(0,0), (500,50),一次 函数yB=0.06x+20的图象过点(0,20),(500,50),其图象如图所示.
(2)通过观察图象可知,当每月上网时间少于500 min时,选择方式A更合算;当每月上网时间为500 min时,两种上网方式 所需费用相同;当每月上网时间多于500 min时,选择方式B更合算.
探索新知
总 结
利用一次函数的图象解决实际问题这类题是近几年中考中的热点问题.运用一次函数的知识判断何种方式更合算时,常通过观察函数图象得到.
探索新知
例4 我边防局接到情报,近海处有一可疑船只A正向公海方向行驶.边防局迅速派出快艇B追赶(如图). 图中l1,l2分别表示两船相对于海岸的距离s (n mile )与追赶时间t(min)之间的关系.根据图象回答下列问题:
探索新知
(1)哪条线表示B到海岸的距离与追赶时间之间的关系?
(2)A, B哪个速度快?
(3)15min内B能否追上A
(4)如果一直追下去,那么B能否追上A
(5)当A逃到离海岸12 n mile的公海时,B将无法对其进行检查.照此速度,B能否在A逃入公海前将其拦截?
(6)l1与l2对应的两个一次函数s = k1t+b1与s = k2t+b2中,k1,k2的实际意义各是什么?可疑船只A与快艇B的速度各是多少
探索新知
解:(1)当t= 0时,B距海岸0nmile,即s = 0,故l1表示B到
海岸的距离与追赶时间之间的关系.
(2)t从0增加到10时,l2的纵坐标增加了 2,而l1的
纵坐标增加了 5, 即10min内,A行驶了 2nmile,
B行驶了5nmile,所以B的速度快.
(3)延长l1,l2(如图),可以看出,
当t= 15时,l1上的对应点在
l2上对应点的下方,这表明,
15 min时B尚未追上A.
探索新知
(4)如图,l1,l2相交于点P.因此,如果一直追下去, 那么B一定能追上A.
(5)图中,l1与l2交点P的纵坐标小于12,这说明, 在A逃入公海前,B能够追上A.
(6)k1表示快艇B的速度, k2表示可疑船只A的速度.可疑船只A的速度是0.2 n mile/min, 快艇B的速度是0.5 n mile/min.
典题精讲
1
甲、乙两商店销售同一种产品的销售价y(元)与销售量x(件)之间的图象如图所示.下列说法:①买2件甲、乙两家销售价一样;②买1件买乙家的合算;③买3件买甲家的合算;④买乙家的1件销售价约为3元,其中正确的说法是( )
A.①②
B.②③④
C.②③
D.①②③
D
典题精讲
2
在一次800 m的长跑比赛中,甲、乙两人所跑的路程s(m)与各自所用时间t(s)之间的函数图象分别为线段OA和折线OBCD,则下列说法正确的是( )
A.甲的速度随时间的增加而增大
B.乙的平均速度比甲的平均速度大
C.在起跑后第180 s时,两人相遇
D.在起跑后第50 s时,乙在甲的前面
D
学以致用
小试牛刀
1.一家电信公司给顾客提供两种上网收费方式:方式A以每分0.1元的价格按上网所用时间计算;方式B除收月基费20元外,再以每分0.05元的价格按上网所用时间计费。若上网所用时问为x分,计费为y元,如图,是在同一直角坐标系中,分别描述两种计费方式的函救的图象,有下列结论:①图象甲描述的是方式A;②图象乙描述的是方式B;③当上网所用时间为500分时,选择方式B省钱。
其中,正确结论的个数是( )
A.3 B.2
C.1 D.0
A
小试牛刀
2.如图,是甲、乙两家商店销售同一种产品的销售价y(元)与销售量x(件)之间的函数图象.下列说法:①售2件时甲、乙两家售价一样;②买1件时买乙家的合算;③买3件时买甲家的合算;④买乙家的1件售价约为3元,其中正确的说法是( )
A.①② B.②③④
C.②③ D.①②③
D
小试牛刀
3.甲、乙两个商场出售相同的某种商品,每件售价均为3 000元,并且多买都有一定的优惠.甲商场的优惠条件是:第一件按原售价收费,其余每件优惠30%;乙商场的优惠条件是:每件优惠25%.设所买商品为x件时,甲商场收费为y1元,乙商场收费为y2元.
(1)分别求出y1,y2与x之间的关系式.
(2)当甲、乙两个商场的收费相同时,所买商品为多少件?
(3)当所买商品为5件时,应选择哪个商场更优惠?请说明理由.
小试牛刀
(1)当x=1时,y1=3 000;当x>1时,
y1=3 000+3 000(x-1)×(1-30%)
=2 100x+900.
3 000(x=1),
2 100x+900(x>1且x为整数);
y2=3 000x(1-25%)=2 250x(x为正整数).
(2)当甲、乙两个商场的收费相同时,
2 100x+900=2 250x,解得x=6.故甲、乙两
个商场的收费相同时,所买商品为6件.
解:
所以y1=
小试牛刀
(3)乙商场.理由:当x=5时,
y1=2 100x+900=2 100×5+900=11 400,
y2=2 250x=2 250×5=11 250,
因为11 400>11 250,
所以当所买商品为5件时,
应选择乙商场更优惠.
小试牛刀
4.某种铂金饰品在甲、乙两个商店销售.甲店标价为477元/g,按标价出售,不优惠;乙店标价为530元/g,但若买的铂金饰品质量超过3 g,则超出部分可打八折.
(1)分别写出到甲、乙两个商店购买该种铂金饰品所需费用y(元)和质量x(g)之间的函数表达式;
(2)李阿姨要买一条质量不少于4 g且不超过10 g的此种铂金饰品,到哪个商店购买合算?
小试牛刀
(1)y甲=477x,
530x(0≤x≤3),
424x+318(x>3).
(2)当477x=424x+318时,解得x=6.
即当x=6时,到甲、乙两个商店购买所需费用相同;
当477x<424x+318时,解得x<6,
又x≥4,于是,当4≤x<6时,到甲商店购买合算;
当477x>424x+318时,解得x>6,
又x≤10,于是,当6<x≤10时,到乙商店购买合算.
解:
y乙=
课堂小结
课堂小结
从函数图象得到需要的信息,再求出函数表达式从而解决实际问题和几何问题,是一次函数应用价值的体现,这种题型常与一些热点问题结合,考查学生综合分析问题、解决问题的能力.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
4.4 一次函数的应用
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图,l1反映了某公司产品的销售收入与销售量的关系,l2反映
了该公司产品的销售成本与销售量的关系,根据图象填空:
(1)当销售量为2t时,销售收入=_____元,
销售成本=____元;
(2)当销售量为6t时,销售收入=_____元,
销售成本=____元;
(3)当销售量等于___时,销售收入等于
销售成本;
(4)当销售量____时,该公司盈利(收入大于成本);
当销售量_____时,该公司亏损(收入小于成本);
(5)l1对应的函数表达式是_____,l2对应的函数表达式是_____.
情景导入
想一想
图中,l1对应的一次函数y=k1x+b1中,k1和b1的实际意义各是什么?l2对应的一次函数y=k2x+b2中,k2和b2的实际意义各是什么?
答:k1的实际意义是:每销售1t产品的销售收入;
b1的实际意义是:未销售时,销售收入为0;
k2的实际意义是:每销售1t的销售成本;
b2的实际意义是:未销售时,为销售所花的成本为2000元.
新课精讲
探索新知
1
知识点
从图表中获取信息的应用
公司有330台机器需要一次性运送到某地,计划租用甲、乙两种货车共8辆,已知每辆甲种货车一次最多运送机器45台,租车费用为400元,每辆乙种货车一次最多运送机器30台,租车费用为280元.
例1
探索新知
315
(1)设租用甲种货车x辆(x为非负整数),试填写表格.
表一:
租用甲种货车的数量/辆 3 7 x
租用的甲种货车最多运送机器的数量/台 135
租用的乙种货车最多运送机器的数量/台 150
表二:
租用甲种货车的数量/辆 3 7 x
租用甲种货车的费用/元 2 800
租用乙种货车的费用/元 280
45x
30
-30x+240
1 200
400x
1 400
-280x+2 240
探索新知
能完成此项运送任务的最节省费用的租车方案是
甲种货车6辆,乙种货车2辆.
理由:当租用甲种货车x辆时,
设两种货车的总费用为y元,
则两种货车的总费用
y=400x+(-280x+2 240)=120x+2 240.
解:
(2)给出能完成此项运送任务的最节省费用的租车方
案,并说明理由.
探索新知
又因为45x+(-30x+240)≥330,
所以x≥6. 因为120>0,
所以在函数y=120x+2 240中,y随x的增大而增大.
所以当x=6时,y取得最小值.
即能完成此项运送任务的最节省费用的租车方案是
甲种货车6辆,乙种货车2辆.
典题精讲
1
一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:例如,购买A类会员年卡,一年内游泳20次,消费50+25×20=550元,若一年内在该游泳馆游泳的次数介于45~55次之间,则最省钱的方式为( )
A.购买A类会员年卡 B.购买B类会员年卡
C.购买C类会员年卡 D.不购买会员年卡
会员年卡类型 办卡费用/元 每次游泳收费/元
A类 50 25
B类 200 20
C类 400 15
C
探索新知
2
知识点
从函数图象中获取信息的应用
例2 游泳池常需进行换水清洗,图中的折线 表示的是游泳池换水清洗过程“排水——清洗——灌水”中 水量y(m3)与时间t(min)之间的函数图象.
(1)根据图中提供的信息,求排水阶段和
清洗阶段游泳池中的水量y(m3)与时间
t(min)之间的函数关系式(不必写出t的
取值范围);
(2)问:排水、清洗各花多少时间?
探索新知
导引:(1)根据图象上点的坐标利用待定系数法求得排水阶段的函数关系式,显然清洗阶段的函数 关系式为y=0;
(2)根据(1)中所求函数关系式,可得出函数图象与x轴的交点坐标,即可得出答案.
探索新知
知识点
解:(1)排水阶段:设y与t之间的函数关系式为y=kt+b,
因为图象经过点(0,1 500),(25,1 000),
所以b=1 500,25k+b=1 000,解得k=-20.
故排水阶段y与t之间的函数关系式为y=-20t+1 500;
清洗阶段y与t之间的函数关系式为y=0.
(2)因为排水阶段y与t之间的函数关系式为y=-20t+1 500,
所以y=0时,0=-20t+1 500,解得t=75.
故排水时间为75 min,清洗时间为95-75=20(min).
探索新知
总 结
此题主要考查了用待定系数法求一次函数的关系式及函数图象与x轴交点坐标的求法,根据图象得出正确的信息是解题关键.
探索新知
知识点
例3 手机上网已经成为当今年轻人时尚的网络生活,某网络公司看中了这种商机,推出了两种手机上网的计费方式:方式A以每分钟0.1元的价格按上网时间计费;方式B除收月租费20元外,再以每分钟0.06元的价格按上网时间计费.假设某客户月上网时间为x min,上网费用为y元.
(1)分别写出该客户按A,B两种方式的上网费用
y(元)与每月上网时间x(min)的函数关系式,
并在图所示的坐标系中画出这两个函数的图象;
(2)如何选择计费方式能使该客户上网费用更合算?
探索新知
知识点
导引:(1)根据题意可直接写出A,B两种上网方式的上网费用y(元)与每月上网时间x(min)的函数关系式,再分别取x的一些特殊值,如0,500,算出对应的y值,根据一次函数的图象是一条直线,分别过求得的两点画直线即可画出这两个函数的图象;(2)根据题意并观察图象可得到不同上网时间范围内选择何种计费方式上网更合算.
解:(1)设方式A:yA=k1x,方式B:yB=k2x+b.
由题意易求得yA=0.1x,yB=0.06x+20,
当x=0时,yA=0,yB=20;
当x=500时,yA=50,yB=50,
探索新知
所以一次函数yA=0.1x的图象过点(0,0), (500,50),一次 函数yB=0.06x+20的图象过点(0,20),(500,50),其图象如图所示.
(2)通过观察图象可知,当每月上网时间少于500 min时,选择方式A更合算;当每月上网时间为500 min时,两种上网方式 所需费用相同;当每月上网时间多于500 min时,选择方式B更合算.
探索新知
总 结
利用一次函数的图象解决实际问题这类题是近几年中考中的热点问题.运用一次函数的知识判断何种方式更合算时,常通过观察函数图象得到.
探索新知
例4 我边防局接到情报,近海处有一可疑船只A正向公海方向行驶.边防局迅速派出快艇B追赶(如图). 图中l1,l2分别表示两船相对于海岸的距离s (n mile )与追赶时间t(min)之间的关系.根据图象回答下列问题:
探索新知
(1)哪条线表示B到海岸的距离与追赶时间之间的关系?
(2)A, B哪个速度快?
(3)15min内B能否追上A
(4)如果一直追下去,那么B能否追上A
(5)当A逃到离海岸12 n mile的公海时,B将无法对其进行检查.照此速度,B能否在A逃入公海前将其拦截?
(6)l1与l2对应的两个一次函数s = k1t+b1与s = k2t+b2中,k1,k2的实际意义各是什么?可疑船只A与快艇B的速度各是多少
探索新知
解:(1)当t= 0时,B距海岸0nmile,即s = 0,故l1表示B到
海岸的距离与追赶时间之间的关系.
(2)t从0增加到10时,l2的纵坐标增加了 2,而l1的
纵坐标增加了 5, 即10min内,A行驶了 2nmile,
B行驶了5nmile,所以B的速度快.
(3)延长l1,l2(如图),可以看出,
当t= 15时,l1上的对应点在
l2上对应点的下方,这表明,
15 min时B尚未追上A.
探索新知
(4)如图,l1,l2相交于点P.因此,如果一直追下去, 那么B一定能追上A.
(5)图中,l1与l2交点P的纵坐标小于12,这说明, 在A逃入公海前,B能够追上A.
(6)k1表示快艇B的速度, k2表示可疑船只A的速度.可疑船只A的速度是0.2 n mile/min, 快艇B的速度是0.5 n mile/min.
典题精讲
1
甲、乙两商店销售同一种产品的销售价y(元)与销售量x(件)之间的图象如图所示.下列说法:①买2件甲、乙两家销售价一样;②买1件买乙家的合算;③买3件买甲家的合算;④买乙家的1件销售价约为3元,其中正确的说法是( )
A.①②
B.②③④
C.②③
D.①②③
D
典题精讲
2
在一次800 m的长跑比赛中,甲、乙两人所跑的路程s(m)与各自所用时间t(s)之间的函数图象分别为线段OA和折线OBCD,则下列说法正确的是( )
A.甲的速度随时间的增加而增大
B.乙的平均速度比甲的平均速度大
C.在起跑后第180 s时,两人相遇
D.在起跑后第50 s时,乙在甲的前面
D
学以致用
小试牛刀
1.一家电信公司给顾客提供两种上网收费方式:方式A以每分0.1元的价格按上网所用时间计算;方式B除收月基费20元外,再以每分0.05元的价格按上网所用时间计费。若上网所用时问为x分,计费为y元,如图,是在同一直角坐标系中,分别描述两种计费方式的函救的图象,有下列结论:①图象甲描述的是方式A;②图象乙描述的是方式B;③当上网所用时间为500分时,选择方式B省钱。
其中,正确结论的个数是( )
A.3 B.2
C.1 D.0
A
小试牛刀
2.如图,是甲、乙两家商店销售同一种产品的销售价y(元)与销售量x(件)之间的函数图象.下列说法:①售2件时甲、乙两家售价一样;②买1件时买乙家的合算;③买3件时买甲家的合算;④买乙家的1件售价约为3元,其中正确的说法是( )
A.①② B.②③④
C.②③ D.①②③
D
小试牛刀
3.甲、乙两个商场出售相同的某种商品,每件售价均为3 000元,并且多买都有一定的优惠.甲商场的优惠条件是:第一件按原售价收费,其余每件优惠30%;乙商场的优惠条件是:每件优惠25%.设所买商品为x件时,甲商场收费为y1元,乙商场收费为y2元.
(1)分别求出y1,y2与x之间的关系式.
(2)当甲、乙两个商场的收费相同时,所买商品为多少件?
(3)当所买商品为5件时,应选择哪个商场更优惠?请说明理由.
小试牛刀
(1)当x=1时,y1=3 000;当x>1时,
y1=3 000+3 000(x-1)×(1-30%)
=2 100x+900.
3 000(x=1),
2 100x+900(x>1且x为整数);
y2=3 000x(1-25%)=2 250x(x为正整数).
(2)当甲、乙两个商场的收费相同时,
2 100x+900=2 250x,解得x=6.故甲、乙两
个商场的收费相同时,所买商品为6件.
解:
所以y1=
小试牛刀
(3)乙商场.理由:当x=5时,
y1=2 100x+900=2 100×5+900=11 400,
y2=2 250x=2 250×5=11 250,
因为11 400>11 250,
所以当所买商品为5件时,
应选择乙商场更优惠.
小试牛刀
4.某种铂金饰品在甲、乙两个商店销售.甲店标价为477元/g,按标价出售,不优惠;乙店标价为530元/g,但若买的铂金饰品质量超过3 g,则超出部分可打八折.
(1)分别写出到甲、乙两个商店购买该种铂金饰品所需费用y(元)和质量x(g)之间的函数表达式;
(2)李阿姨要买一条质量不少于4 g且不超过10 g的此种铂金饰品,到哪个商店购买合算?
小试牛刀
(1)y甲=477x,
530x(0≤x≤3),
424x+318(x>3).
(2)当477x=424x+318时,解得x=6.
即当x=6时,到甲、乙两个商店购买所需费用相同;
当477x<424x+318时,解得x<6,
又x≥4,于是,当4≤x<6时,到甲商店购买合算;
当477x>424x+318时,解得x>6,
又x≤10,于是,当6<x≤10时,到乙商店购买合算.
解:
y乙=
课堂小结
课堂小结
从函数图象得到需要的信息,再求出函数表达式从而解决实际问题和几何问题,是一次函数应用价值的体现,这种题型常与一些热点问题结合,考查学生综合分析问题、解决问题的能力.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
