北师大版(新)八上-4.4 一次函数的应用 第一课时【优质课件】
文档属性
| 名称 | 北师大版(新)八上-4.4 一次函数的应用 第一课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:52:29 | ||
图片预览









文档简介
(共38张PPT)
4.4 一次函数的应用
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
(1)若y=kx+b(k,b为常数,k≠0),则称y是x的一次函数.
复
习
回
顾
(2) y=kx(k≠0)则y是x的正比例函数.
(3)一次函数y=kx+b有下列性质:
当k>0时,y随x的增大而增大.
当k<0时,y随x的增大而减小.
新课精讲
探索新知
1
知识点
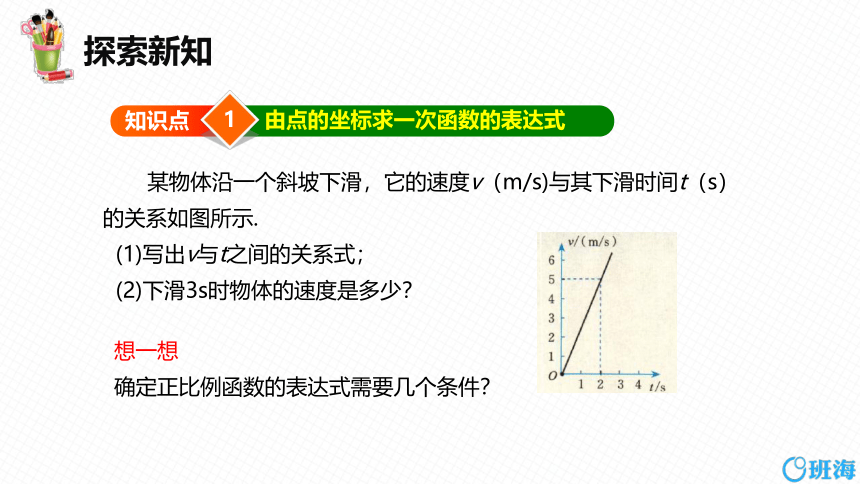
由点的坐标求一次函数的表达式
某物体沿一个斜坡下滑,它的速度v(m/s)与其下滑时间t(s)
的关系如图所示.
(1)写出v与t之间的关系式;
(2)下滑3s时物体的速度是多少?
想一想
确定正比例函数的表达式需要几个条件?
探索新知
例1 已知:y与2x成正比例,且当x=3时,y=12,求y与x的函数关系式.
导引:根据正比例函数的定义,按求正比例函数关系式的步骤求解.
解:设y=k·2x(k≠0).
因为当x=3时,y=12,
所以12=2×3×k.所以k=2.
所以所求的函数关系式为y=4x.
探索新知
知识点
例2 如图,直线l是一次函数y=kx+b(k≠0)的图象.
求:(1)直线l对应的函数表达式;
(2)当y=2时,x的值.
导引:(1)根据一次函数图象上两点的坐标,
可列出方程,解出k,b的值即可.
(2)把y=2代入所求出的函数表达式即可得到x的值.
探索新知
解:(1)由图可知,直线l经过点(-2,0)和点(0,3),
将其坐标代入一次函数表达式y=kx+b,
得到-2k+b=0,b=3.
解得k= ,则直线l对应的函数表达式为
y= x+3.
(2)当y=2时,有2= x+3.解得x=- .
探索新知
总 结
由图象求一次函数的表达式,关键是找出图象上的两点,将其坐标代入表达式,解出k和b的值即可.选取点时一般取图象与x轴和y轴的交点,以便求解.
典题精讲
1
已知正比例函数y=kx(k≠0)的图象经过点(1,-2),则这个正比例函数的表达式为( )
A.y=2x B.y=-2x
C.y= x D.y=- x
B
典题精讲
2
已知正比例函数y=kx(k≠0)的图象如图所示,则在下列选项中k值可能是( )
A.1
B.2
C.3
D.4
B
探索新知
1、两条直线平行的规律:
两条直线平行 k值相等
2、平移规律:“上加下减”,上、下是形的平移,加、减是数的变化:
直线y=kx+b可以看作由直线 y=kx平移得到:
①当b>0时,把直线y=kx向上平移b个单位得到直线y=kx+b;
②当b<0时,把直线y=kx向下平移|b|个单位得到直线y=kx+b.
2
知识点
由直线的位置变换求一次函数的表达式
探索新知
知识点
例3 一个一次函数的图象平行于直线y=-2x,且
过点A(-4,2),求这个函数的表达式.
解:∵一次函数图象与直线y= -2x平行,
∴设y= -2x +b,
把点A(-4, 2)代入上式得,
2= -2×(-4)+b,
∴b= -6.
∴这个函数的表达式为y= -2x -6.
典题精讲
若直线l与直线y=2x-3关于x轴对称,则直线l的表达式为( )
A.y=-2x-3 B.y=-2x+3
C.y= x+3 D.y=- x-3
1
B
典题精讲
如图,把直线l向上平移2个单位得到直线l′,则l′的表达式为( )
A.y= x+1
B.y= x-1
C.y=- x-1
D.y=- x+1
2
D
探索新知
3
知识点
由几何图形性质求一次函数的表达式
如图,直线y= x+ 与两坐标轴分别交于A,B两点.
(1)求AB的长;
(2)过A的直线l交x轴正半轴于
C,AB=AC,求直线l对应
的函数表达式.
例4
探索新知
知识点
(1)对于直线y= x+ ,
令x=0,则y= ,
令y=0,则x=-1,
所以点A的坐标为(0, ),
点B的坐标为(-1,0).
所以AO= ,BO=1,
在Rt△ABO中,
AB=
解:
探索新知
知识点
(2)在△ABC中,
因为AB=AC,AO⊥BC,
所以BO=CO.
所以C点的坐标为(1,0).
设直线l对应的函数表达式为y=kx+b(k,b为常数),
则b= ,且k+b=0,
解得k=- ,b= .
即直线l对应的函数表达式为y=- x+ .
解:
典题精讲
如图,直线y= x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点.PC+PD值最小时点P的坐标为( )
A.(-3,0)
B.(-6,0)
C.
D.
1
C
探索新知
4
知识点
由数量关系求一次函数的表达式
为了提高身体素质,有些人选择到专业的健身中心锻炼身体,某健身中心的消费方式如下:普通消费:35元/次;白金卡消费:购卡280元/张,凭卡免费消费10次再送2次;钻石卡消费:购卡560元/张,凭卡每次消费不再收费.以上消费卡使用年限均为一年,每位顾客只能购买一张卡,且只限本人使用.
例5
探索新知
知识点
35×6=210(元),
210<280<560,
所以李叔叔应选择普通消费最合算.
解:
(1)李叔叔每年去该健身中心健身6次,他应选择哪种消费方式最合算?
探索新知
知识点
根据题意得y普通=35x(x为正整数).
当x≤12时,y白金卡=280;
当x>12时,y白金卡=280+35(x-12)=35x-140.
所以y白金卡=
解:
(2)设一年内去该健身中心健身x次(x为正整数),所需总费用为y元,请分别写出选择普通消费和白金卡消费的y与x的函数关系式.
探索新知
知识点
当x=18时,y普通=35×18=630;
y白金卡=35×18-140=490;
令y白金卡=560,即35x-140=560,解得x=20.
当18≤x≤19时,选择白金卡消费最合算;
当x=20时,选择白金卡消费和钻石卡消费费用相同;
当x≥21时,选择钻石卡消费最合算.
解:
(3)王阿姨每年去健身中心健身至少18次,请通过计算帮助王阿姨选择最合算的消费方式.
典题精讲
用每张长6 cm的纸条,重叠1 cm粘贴成一条纸带,如图.纸带的长度y(cm)与纸条的张数x之间的函数表达式是( )
A.y=6x+1 B.y=4x+1
C.y=4x+2 D.y=5x+1
D
学以致用
小试牛刀
1.若一次函数y=kx-3k+6的图象过原点,则k=_______,一次函数的解析式为________.
2.若y-1与x成正比例,且当x=-2时,y=4,那么y与x之间的函数关系式为________________.
3.如图,直线AB是一次函数y=kx+b的图象,若|AB|= ,则函数的表达式为________________.
2
2x
y=- x+1
y=-2x+2
小试牛刀
4.随着我国人口增长速度的减慢,小学入学儿童数量有所减少.下表中的数据近似地呈现了某地区入学儿童人数的变化趋势.
利用你所学的函数知识解决以下问题:
①入学儿童人数y(人)与年份x(年)的函数关系是__________________________.
②预测该地区从______________年起入学儿童人数不超过1000人.
年份(x) 1999 2000 2001 2002 …
入学儿童人数(y) 2710 2520 2330 2140 …
2008
y=2710-190(x-1999)
小试牛刀
5.一次函数的图象过点M(3,2),N(-1,-6)两点 .
(1)求函数的表达式;
解:(1)设函数的表达式为y=kx+b,根据题意,得
3k+b =2 ①
-k+b=-6 ②
由①得 b=2-3k;由②得 b=k-6
所以z-3k=k- 6,即k=2
把 k=2代入②,得 b=-4
所以y与x间的关系为:y=2x-4.
小试牛刀
图象如下图,由y=2x-4 知,图象与x轴、y轴的交点坐标分别为(2,0),(0,-4).
5.一次函数的图象过点M(3,2),N(-1,-6)两点 .
(2)画出该函数的图象.
小试牛刀
6 .在直角坐标系中,一次函数y=kx+b的图象经 过三点A(2,0),B(0,2),C(m,3),求这个函数的表达式,并求m的值.
解:根据题意, 得
2k+b=0 ①
b=2 ②
km+b=3 ③
把b=2代入①,得2k+2=0
即k=-1
把b=2,k=-1代入③,得m=-1
即 函数的表达式为y=-x+2,m的值为-1
小试牛刀
7.小明买了一套现价为12万元的房子,购房时已付房款3万元,从第二年起,以后每年付房款5000元与上一年剩余欠款利息的和,已知剩余欠款的年利率为0.4%.
(1)将第三年、第四年、第十年应付房款填入下列表格中:
年份 第一年 第二年 第三年 第四年 … 第十年 …
应交房款(元) 30000 5360 … …
(2)若第x年(x≥2),小明家应交房款y元,请写出年付房款y与x的函数关系式. ___________________________________________________________.
5340
5320
5200
y=5000+[90000-5000(x-2)]×0.4%=5400-20x(x≥2)
小试牛刀
8.明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
A. 300m2
B. 150m2
C. 330m2
D. 450m2
B
小试牛刀
解:如图,
设直线AB的解析式为y=kx+b,则
4k+b=1200; 5k+b=1650,
解得k=450,b=-600.
故直线AB的解析式为y=450x-600,
当x=2时,y=450×2-600=300,
300÷2=150(m ).
答:该绿化组提高工作效率前每小时完成的绿化面积是150m .
小试牛刀
9.如图,一次函数图象经过点A,且与正比例函数y=-x的图象交于点B,则该一次函数的表达式为______________.
设解析式为y=kx+b,
将x=-1代入y=-x,得y=1;则B点坐标为(-1,1),将(-1,1)和(0,2)代入y=kx+b;
得 -k+b=1 b=2 ,
解得 b=2 k=1 ;
∴解析式为:y=x+2.
y=x+2
课堂小结
课堂小结
1.确定一次函数的关系式,就是确定一次函数关系式y=kx+b(k≠0)中常数k , b的值.
2. 求一次函数关系式的步骤为:
设→代→求→还原,即:
(1)设:设出一次函数关系式y=kx+b;
(2)代:将所给数据代入函数关系式;
(3)求:求出k的值;
(4)还原:写出一次函数关系式.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
4.4 一次函数的应用
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
(1)若y=kx+b(k,b为常数,k≠0),则称y是x的一次函数.
复
习
回
顾
(2) y=kx(k≠0)则y是x的正比例函数.
(3)一次函数y=kx+b有下列性质:
当k>0时,y随x的增大而增大.
当k<0时,y随x的增大而减小.
新课精讲
探索新知
1
知识点
由点的坐标求一次函数的表达式
某物体沿一个斜坡下滑,它的速度v(m/s)与其下滑时间t(s)
的关系如图所示.
(1)写出v与t之间的关系式;
(2)下滑3s时物体的速度是多少?
想一想
确定正比例函数的表达式需要几个条件?
探索新知
例1 已知:y与2x成正比例,且当x=3时,y=12,求y与x的函数关系式.
导引:根据正比例函数的定义,按求正比例函数关系式的步骤求解.
解:设y=k·2x(k≠0).
因为当x=3时,y=12,
所以12=2×3×k.所以k=2.
所以所求的函数关系式为y=4x.
探索新知
知识点
例2 如图,直线l是一次函数y=kx+b(k≠0)的图象.
求:(1)直线l对应的函数表达式;
(2)当y=2时,x的值.
导引:(1)根据一次函数图象上两点的坐标,
可列出方程,解出k,b的值即可.
(2)把y=2代入所求出的函数表达式即可得到x的值.
探索新知
解:(1)由图可知,直线l经过点(-2,0)和点(0,3),
将其坐标代入一次函数表达式y=kx+b,
得到-2k+b=0,b=3.
解得k= ,则直线l对应的函数表达式为
y= x+3.
(2)当y=2时,有2= x+3.解得x=- .
探索新知
总 结
由图象求一次函数的表达式,关键是找出图象上的两点,将其坐标代入表达式,解出k和b的值即可.选取点时一般取图象与x轴和y轴的交点,以便求解.
典题精讲
1
已知正比例函数y=kx(k≠0)的图象经过点(1,-2),则这个正比例函数的表达式为( )
A.y=2x B.y=-2x
C.y= x D.y=- x
B
典题精讲
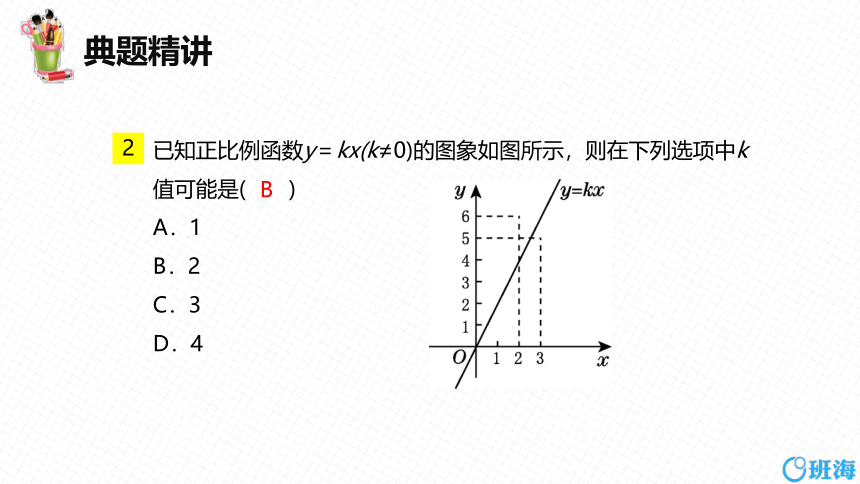
2
已知正比例函数y=kx(k≠0)的图象如图所示,则在下列选项中k值可能是( )
A.1
B.2
C.3
D.4
B
探索新知
1、两条直线平行的规律:
两条直线平行 k值相等
2、平移规律:“上加下减”,上、下是形的平移,加、减是数的变化:
直线y=kx+b可以看作由直线 y=kx平移得到:
①当b>0时,把直线y=kx向上平移b个单位得到直线y=kx+b;
②当b<0时,把直线y=kx向下平移|b|个单位得到直线y=kx+b.
2
知识点
由直线的位置变换求一次函数的表达式
探索新知
知识点
例3 一个一次函数的图象平行于直线y=-2x,且
过点A(-4,2),求这个函数的表达式.
解:∵一次函数图象与直线y= -2x平行,
∴设y= -2x +b,
把点A(-4, 2)代入上式得,
2= -2×(-4)+b,
∴b= -6.
∴这个函数的表达式为y= -2x -6.
典题精讲
若直线l与直线y=2x-3关于x轴对称,则直线l的表达式为( )
A.y=-2x-3 B.y=-2x+3
C.y= x+3 D.y=- x-3
1
B
典题精讲
如图,把直线l向上平移2个单位得到直线l′,则l′的表达式为( )
A.y= x+1
B.y= x-1
C.y=- x-1
D.y=- x+1
2
D
探索新知
3
知识点
由几何图形性质求一次函数的表达式
如图,直线y= x+ 与两坐标轴分别交于A,B两点.
(1)求AB的长;
(2)过A的直线l交x轴正半轴于
C,AB=AC,求直线l对应
的函数表达式.
例4
探索新知
知识点
(1)对于直线y= x+ ,
令x=0,则y= ,
令y=0,则x=-1,
所以点A的坐标为(0, ),
点B的坐标为(-1,0).
所以AO= ,BO=1,
在Rt△ABO中,
AB=
解:
探索新知
知识点
(2)在△ABC中,
因为AB=AC,AO⊥BC,
所以BO=CO.
所以C点的坐标为(1,0).
设直线l对应的函数表达式为y=kx+b(k,b为常数),
则b= ,且k+b=0,
解得k=- ,b= .
即直线l对应的函数表达式为y=- x+ .
解:
典题精讲
如图,直线y= x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点.PC+PD值最小时点P的坐标为( )
A.(-3,0)
B.(-6,0)
C.
D.
1
C
探索新知
4
知识点
由数量关系求一次函数的表达式
为了提高身体素质,有些人选择到专业的健身中心锻炼身体,某健身中心的消费方式如下:普通消费:35元/次;白金卡消费:购卡280元/张,凭卡免费消费10次再送2次;钻石卡消费:购卡560元/张,凭卡每次消费不再收费.以上消费卡使用年限均为一年,每位顾客只能购买一张卡,且只限本人使用.
例5
探索新知
知识点
35×6=210(元),
210<280<560,
所以李叔叔应选择普通消费最合算.
解:
(1)李叔叔每年去该健身中心健身6次,他应选择哪种消费方式最合算?
探索新知
知识点
根据题意得y普通=35x(x为正整数).
当x≤12时,y白金卡=280;
当x>12时,y白金卡=280+35(x-12)=35x-140.
所以y白金卡=
解:
(2)设一年内去该健身中心健身x次(x为正整数),所需总费用为y元,请分别写出选择普通消费和白金卡消费的y与x的函数关系式.
探索新知
知识点
当x=18时,y普通=35×18=630;
y白金卡=35×18-140=490;
令y白金卡=560,即35x-140=560,解得x=20.
当18≤x≤19时,选择白金卡消费最合算;
当x=20时,选择白金卡消费和钻石卡消费费用相同;
当x≥21时,选择钻石卡消费最合算.
解:
(3)王阿姨每年去健身中心健身至少18次,请通过计算帮助王阿姨选择最合算的消费方式.
典题精讲
用每张长6 cm的纸条,重叠1 cm粘贴成一条纸带,如图.纸带的长度y(cm)与纸条的张数x之间的函数表达式是( )
A.y=6x+1 B.y=4x+1
C.y=4x+2 D.y=5x+1
D
学以致用
小试牛刀
1.若一次函数y=kx-3k+6的图象过原点,则k=_______,一次函数的解析式为________.
2.若y-1与x成正比例,且当x=-2时,y=4,那么y与x之间的函数关系式为________________.
3.如图,直线AB是一次函数y=kx+b的图象,若|AB|= ,则函数的表达式为________________.
2
2x
y=- x+1
y=-2x+2
小试牛刀
4.随着我国人口增长速度的减慢,小学入学儿童数量有所减少.下表中的数据近似地呈现了某地区入学儿童人数的变化趋势.
利用你所学的函数知识解决以下问题:
①入学儿童人数y(人)与年份x(年)的函数关系是__________________________.
②预测该地区从______________年起入学儿童人数不超过1000人.
年份(x) 1999 2000 2001 2002 …
入学儿童人数(y) 2710 2520 2330 2140 …
2008
y=2710-190(x-1999)
小试牛刀
5.一次函数的图象过点M(3,2),N(-1,-6)两点 .
(1)求函数的表达式;
解:(1)设函数的表达式为y=kx+b,根据题意,得
3k+b =2 ①
-k+b=-6 ②
由①得 b=2-3k;由②得 b=k-6
所以z-3k=k- 6,即k=2
把 k=2代入②,得 b=-4
所以y与x间的关系为:y=2x-4.
小试牛刀
图象如下图,由y=2x-4 知,图象与x轴、y轴的交点坐标分别为(2,0),(0,-4).
5.一次函数的图象过点M(3,2),N(-1,-6)两点 .
(2)画出该函数的图象.
小试牛刀
6 .在直角坐标系中,一次函数y=kx+b的图象经 过三点A(2,0),B(0,2),C(m,3),求这个函数的表达式,并求m的值.
解:根据题意, 得
2k+b=0 ①
b=2 ②
km+b=3 ③
把b=2代入①,得2k+2=0
即k=-1
把b=2,k=-1代入③,得m=-1
即 函数的表达式为y=-x+2,m的值为-1
小试牛刀
7.小明买了一套现价为12万元的房子,购房时已付房款3万元,从第二年起,以后每年付房款5000元与上一年剩余欠款利息的和,已知剩余欠款的年利率为0.4%.
(1)将第三年、第四年、第十年应付房款填入下列表格中:
年份 第一年 第二年 第三年 第四年 … 第十年 …
应交房款(元) 30000 5360 … …
(2)若第x年(x≥2),小明家应交房款y元,请写出年付房款y与x的函数关系式. ___________________________________________________________.
5340
5320
5200
y=5000+[90000-5000(x-2)]×0.4%=5400-20x(x≥2)
小试牛刀
8.明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
A. 300m2
B. 150m2
C. 330m2
D. 450m2
B
小试牛刀
解:如图,
设直线AB的解析式为y=kx+b,则
4k+b=1200; 5k+b=1650,
解得k=450,b=-600.
故直线AB的解析式为y=450x-600,
当x=2时,y=450×2-600=300,
300÷2=150(m ).
答:该绿化组提高工作效率前每小时完成的绿化面积是150m .
小试牛刀
9.如图,一次函数图象经过点A,且与正比例函数y=-x的图象交于点B,则该一次函数的表达式为______________.
设解析式为y=kx+b,
将x=-1代入y=-x,得y=1;则B点坐标为(-1,1),将(-1,1)和(0,2)代入y=kx+b;
得 -k+b=1 b=2 ,
解得 b=2 k=1 ;
∴解析式为:y=x+2.
y=x+2
课堂小结
课堂小结
1.确定一次函数的关系式,就是确定一次函数关系式y=kx+b(k≠0)中常数k , b的值.
2. 求一次函数关系式的步骤为:
设→代→求→还原,即:
(1)设:设出一次函数关系式y=kx+b;
(2)代:将所给数据代入函数关系式;
(3)求:求出k的值;
(4)还原:写出一次函数关系式.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
