北师大版(新)八上-5.4 应用二元一次方程组——增收节支 第二课时【优质课件】
文档属性
| 名称 | 北师大版(新)八上-5.4 应用二元一次方程组——增收节支 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:52:29 | ||
图片预览










文档简介
(共42张PPT)
5.4 应用二元一次方程组——增收节支
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
列方程解生活中的问题
关系
( 1 )路程=速度×时间;
( 2 ) 顺水速度 = 静水速度+水流速度,
逆水速度=靜水速度-水流速度;
( 3 ) 工作量=工作效率×工作时间;
( 4 ) 利润=销售价-进货价,
利润 = 成本价(进货价)x利润率;
( 5 ) 利息 = 本金×利率 ×期数 × ( 1 一税率),
本息和=本金-利息
新课精讲
探索新知
1
题型
行程问题
基本关系式:
相遇问题:同时不同地相向而行时,两人走的路程之和=两地距离.
追及问题:同地不同时同向而行时,前者走的路程=追者走的路程;同时不同地同向而行时,两人走的路程之差=两地距离.
航行问题:顺流速度=静水速度+水流速度;逆流速度=静水速度-水流速度.
探索新知
甲、乙两人分别从相距40 km的两地同时出发,若同向而行,则5 h后,快者追上慢者;若相向而行,则2 h后,两人相遇,那么快者速度和慢者速度(单位:km/h)分别是( )
A.14和6 B.24和16
C.28和12 D.30和10
应用1
相遇(追及)问题
A
探索新知
同类变式
张明沿公路匀速前进,每隔4 min就遇到迎面开来的一辆公共汽车,每隔6 min就有一辆公共汽车从背后超过他.假定公共汽车的速度相同,且不变,而且迎面开来的相邻两车的距离和从背后开来的相邻两车的距离都是1 200 m,求张明前进的速度和公共汽车的速度.
2.
探索新知
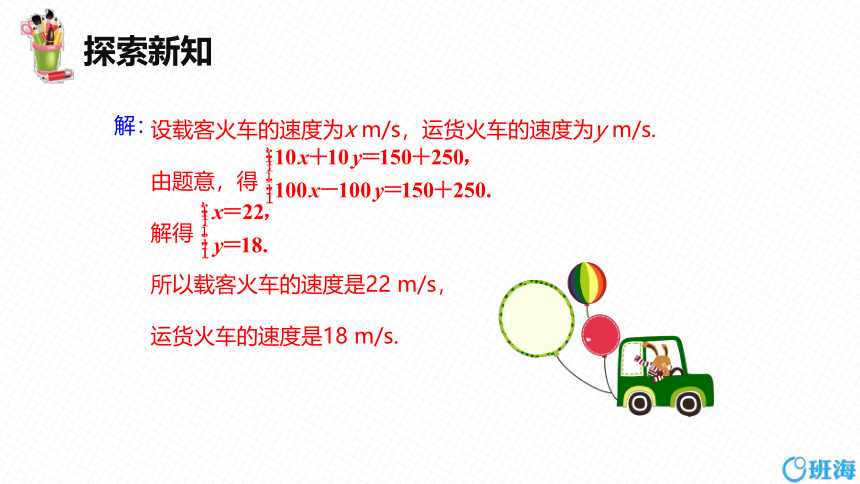
3.一列载客火车和一列运货火车分别在两条平行的铁轨上行驶,载客火车长150 m,运货火车长250 m.若两车相向而行,从车头相遇到车尾离开共需10 s;若载客火车从后面追赶运货火车,从车头追上运货火车车尾到完全超过运货火车共需100 s.试求两车的速度.
应用2
错车问题
探索新知
设载客火车的速度为x m/s,运货火车的速度为y m/s.
由题意,得
解得
所以载客火车的速度是22 m/s,
运货火车的速度是18 m/s.
解:
探索新知
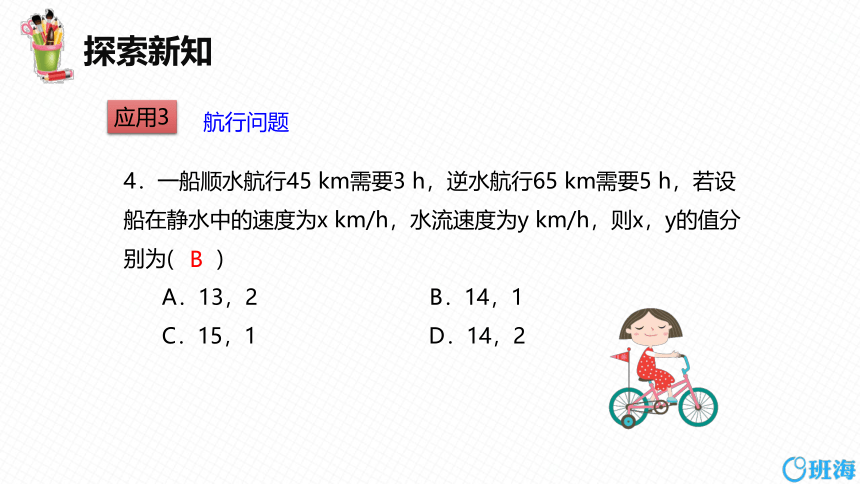
4.一船顺水航行45 km需要3 h,逆水航行65 km需要5 h,若设船在静水中的速度为x km/h,水流速度为y km/h,则x,y的值分别为( )
A.13,2 B.14,1
C.15,1 D.14,2
应用3
航行问题
B
探索新知
5.甲、乙二人在一环形场地上从A点同时同向匀速跑步,甲的速度是乙的2.5倍,4 min后两人首次相遇,此时乙还需要跑300 m才跑完第一圈.求甲、乙二人的速度及环形场地的周长.
应用4
环形跑道问题
探索新知
设乙的速度为x m/min,环形场地的周长为y m,
则甲的速度为2.5x m/min,
由题意,得
解得
2.5×150=375.
所以甲的速度为375 m/min,乙的速度为150 m/min,环形场地的周长为900 m.
解:
探索新知
6.A,B两镇相距12 km,甲从A镇、乙从B镇骑车同时出发,相向而行,设甲、乙行驶的速度分别为u km/h,υ km/h. ①出发后30 min相遇;②甲行驶的速度比乙行驶的速度快8 km/h,试根据题意,由条件列出方程组,并求解.
应用5
一般问题
由题意,得
解得
所以甲的速度为16 km/h,乙的速度为8 km/h.
解:
探索新知
同类变式
某人骑自行车从A地先以12 km/h的速度下坡后,再以9 km/h的速度走平路到B地,共用了55 min.回来时他以8 km/h的速度通过平路后,以4 km/h的速度上坡,从B地到A地共用了1.5 h.求A,B两地相距多少千米.
7.
探索新知
2
配套问题
题型
8. 某商场计划拨款9万元从厂家购进50台电冰箱,已知该厂家生产三种不同型号的电冰箱,出厂价分别为:甲种每台1 500元,乙种每台2 100元,丙种每台2 500元.
(1)该商场同时购进其中两种不同型号电冰箱共50台,用去9万元,请你研究一下商场的进货方案;
应用1
购物配套问题
探索新知
①设购进甲种电冰箱x台,购进乙种电冰箱y台,根据题意,得
解得
故第一种进货方案是购进甲、乙两种型号的电冰箱各25台.
解:
探索新知
②设购进甲种电冰箱x台,购进丙种电冰箱z台,
根据题意,得
解得
故第二种进货方案是购进甲种电冰箱35台,丙种电冰箱15台.
探索新知
③设购进乙种电冰箱y台,购进丙种电冰箱z台,
根据题意,得
解得
不合题意,舍去.故此种方案不可行.综上,商场共有两种进货方案,
方案一,购进甲、乙两种型号的电冰箱各25台;
方案二,购进甲种电冰箱35台,丙种电冰箱15台.
探索新知
(2)该商场销售一台甲种电冰箱可获利150元,销售一台乙种电冰箱可获利200元,销售一台丙种电冰箱可获利250元,在同时购进两种不同型号的方案中,为使销售时获利最多,应选择哪种进货方案?
第一种方案可获利150×25+200×25=8 750(元),
第二种方案可获利150×35+250×15=9 000(元).
因为8 750<9 000,所以应选择第二种进货方案,
即购进甲种电冰箱35台,丙种电冰箱15台.
解:
探索新知
9.食品安全是关乎民生的重要问题,在食品中添加过量的添加剂对人体健康有害,但适量的添加剂对人体无害而且有利于食品的储存和运输.为提高质量,做进一步研究.某饮料加工厂需生产A,B两种饮料共100瓶,需加入同种添加剂270 g,其中A饮料每瓶需加该添加剂2 g,B饮料每瓶需加该添加剂3 g,饮料加工厂生产了A,B两种饮料各多少瓶?
应用2
生产配套问题
探索新知
设饮料加工厂生产了A种饮料x瓶,B种饮料y瓶,根据题意,得
解得
所以饮料加工厂生产了A种饮料30瓶,B种饮料70瓶.
解:
探索新知
10.小颖参加课外兴趣活动时设计了一个圆柱体模型,现有150张白纸,一张白纸可做侧面16个或底面43个,一个侧面与两个底面配成一套模型,则用多少张纸制底面,多少张纸制侧面,才能正好配成整套模型?
设用x张纸制底面,y张纸制侧面,
则
解得
故用64张纸制底面,86张纸制侧面,才能正好配成整套模型.
解:
探索新知
某地生产一种绿色蔬菜,若在市场上直接销售,每吨的利润为1 000 元;经粗加工后销售,每吨的利润可达4 500 元;经精加工后销售,每吨的利润涨至7 500元.当地一家农工商公司收购这种蔬菜140 t,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16 t;如果进行精加工,每天可加工6 t,但两种加工方式不能同时进行.受季节条件的限制,公司必须在15天之内将这批蔬菜处理完毕,为此公司给出了三种加工方案:
11.
探索新知
方案1:将蔬菜全部进行粗加工;
方案2:尽可能多地对蔬菜进行精加工,没有来得及
加工的蔬菜在市场上直接销售;
方案3:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好在15天之内完成.
你认为选择哪种方案获利最多?
方案1获利为4 500×140=630 000(元).
方案2获利为7 500×6×15+1 000×(140-6×15)
=675 000+50 000=725 000(元).
解:
探索新知
方案3:设将x t蔬菜进行精加工,y t蔬菜进行粗加工.
根据题意,得
解得
所以方案3获利为7 500×60+4 500×80=810 000(元).
因为630 000<725 000<810 000,
所以选择方案3获利最多.
探索新知
12.某水果基地计划装运甲、乙、丙三种水果到外地销售(每辆汽车按规定满载,并且只装一种水果).下表为装运甲、乙、丙三种水果的质量及利润.
应用3
运输配套问题
甲 乙 丙
每辆汽车能装的质量/t 4 2 3
每吨水果可获利润/千元 5 7 4
探索新知
(1)用8辆汽车装运乙、丙两种水果共22 t到A地销售,问装运乙、丙两种水果的汽车各多少辆?
设装运乙、丙水果的汽车分别为x辆、y辆,
依题意,得
解得
所以装运乙水果的汽车有2辆,丙水果的汽车有6辆.
解:
探索新知
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72 t到B地销售(每种水果不少于一车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆(结果用m表示)
设装运乙、丙水果的汽车分别为a辆、b辆,
依题意,得
解得
所以装运乙水果的汽车是(m-12)辆,
丙水果的汽车是(32-2m)辆.
解:
探索新知
(3)在(2)问的基础上,如何安排装运可使水果基地获得最大利润?最大利润是多少?
设总利润为w千元,
w=5×4m+7×2(m-12)+4×3(32-2m)=10m+216.
因为
所以13≤m≤15.5.
因为m为正整数,所以m=13,14,15.
解:
探索新知
在w=10m+216中,w随m的增大而增大,
所以当m=15时,w最大=366.
所以当安排装运甲水果的汽车为15辆,装运乙水果的汽车为3辆,装运丙水果的汽车为2辆时,利润最大,最大利润为366千元.
求32-2m≥1中m的取值范围时,可先求出32-2m=1中m的值为15.5,所以只有m≤15.5时,32-2m≥1才成立.
点拨:
学以致用
小试牛刀
1.甲、乙二人练习跑步,如果甲让乙先跑10米,甲跑5秒就追上乙,如果甲让乙先跑2秒,那么甲跑4秒就追上乙,
则甲、乙两人的速度分别是__________________.
6米/秒,4米/秒
小试牛刀
2.某高速公路全长约126 km,一辆小汽车、一辆货车同时从巴中、广元两地相向开出,经过45分钟相遇.相遇时小汽车比货车多行6 km.设小汽车和货车的速度分别为x km/h,y km/h,则下列方程组正确的是( )
D
小试牛刀
3.一条船顺流航行,每小时行驶18 km;逆流航行,每小时行驶16 km.若设船在静水中的速度为x km/h,水流速度为y km/h,则列出的方程组为( )
B
小试牛刀
3.李明同学早上骑自行车上学,中途因道路施工步行一段路,到学校共用时15分钟.他骑自行车的平均速度是250米/分钟,步行的平均速度是80米/分钟,他家离学校的距离是2900米.如果他骑车和步行的时间分别为x,y分钟,列出的方程是( )
D
小试牛刀
4.达州景点真佛山的学生门票价格如下表所示:
某校八年级(1),(2)两个班去游览真佛山,其中(1)班人数较少,不足50人,(2)班人数较多,有50多人,两个班合起来超过100人.如果两个班都以班为单位分别购票,那么一共应付1240元;如果两个班联合起来,作为一个团体购票,那么只需付936元.
购票人数 1~50人 51~100人 100人以上
每张门票/元 13 11 9
小试牛刀
(1)列方程或方程组求出两个班各有多少学生;
(2)如果两个班不联合买票,那么八年级(1)班的学生非要买13元的票吗?你有什么省钱方式来帮他们买票吗?说说你的理由;
(3)你认为是否存在这样的可能:51~100人之间买票的钱数与100人以上买票的钱数相等?若有,是多少人与多少人买票钱数相等?
小试牛刀
(2)八年级(1)班的学生不一定非要买13元的票.(1)班可以买51人的票.
理由:由(1)可知八年级(1)班有48人,只需多买3张票,
即可按每张门票11元结算.51×11=561(元),48×13=624(元)>561元,
所以48人买51人的票可以更省钱
(3)存在.设人数在51~100人之间的人数为m,人数在100人以上的人数为n.假设存在买票钱数相等的状况,则满足11m=9n.因为m<100,n>100,所以符合题意的正整数解为m=90,n=110;m=99,n=121.即存在这样的可能,90人与110人,99人与121人买票钱数相等.
课堂小结
课堂小结
方法技能:
解决本节问题的关键是建立数学模型,常借助列表,
分析具体问题中的数量关系,使题目中的等量关系清晰浮现.
易错提示:
解题结果要符合题目的实际意义.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
5.4 应用二元一次方程组——增收节支
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
列方程解生活中的问题
关系
( 1 )路程=速度×时间;
( 2 ) 顺水速度 = 静水速度+水流速度,
逆水速度=靜水速度-水流速度;
( 3 ) 工作量=工作效率×工作时间;
( 4 ) 利润=销售价-进货价,
利润 = 成本价(进货价)x利润率;
( 5 ) 利息 = 本金×利率 ×期数 × ( 1 一税率),
本息和=本金-利息
新课精讲
探索新知
1
题型
行程问题
基本关系式:
相遇问题:同时不同地相向而行时,两人走的路程之和=两地距离.
追及问题:同地不同时同向而行时,前者走的路程=追者走的路程;同时不同地同向而行时,两人走的路程之差=两地距离.
航行问题:顺流速度=静水速度+水流速度;逆流速度=静水速度-水流速度.
探索新知
甲、乙两人分别从相距40 km的两地同时出发,若同向而行,则5 h后,快者追上慢者;若相向而行,则2 h后,两人相遇,那么快者速度和慢者速度(单位:km/h)分别是( )
A.14和6 B.24和16
C.28和12 D.30和10
应用1
相遇(追及)问题
A
探索新知
同类变式
张明沿公路匀速前进,每隔4 min就遇到迎面开来的一辆公共汽车,每隔6 min就有一辆公共汽车从背后超过他.假定公共汽车的速度相同,且不变,而且迎面开来的相邻两车的距离和从背后开来的相邻两车的距离都是1 200 m,求张明前进的速度和公共汽车的速度.
2.
探索新知
3.一列载客火车和一列运货火车分别在两条平行的铁轨上行驶,载客火车长150 m,运货火车长250 m.若两车相向而行,从车头相遇到车尾离开共需10 s;若载客火车从后面追赶运货火车,从车头追上运货火车车尾到完全超过运货火车共需100 s.试求两车的速度.
应用2
错车问题
探索新知
设载客火车的速度为x m/s,运货火车的速度为y m/s.
由题意,得
解得
所以载客火车的速度是22 m/s,
运货火车的速度是18 m/s.
解:
探索新知
4.一船顺水航行45 km需要3 h,逆水航行65 km需要5 h,若设船在静水中的速度为x km/h,水流速度为y km/h,则x,y的值分别为( )
A.13,2 B.14,1
C.15,1 D.14,2
应用3
航行问题
B
探索新知
5.甲、乙二人在一环形场地上从A点同时同向匀速跑步,甲的速度是乙的2.5倍,4 min后两人首次相遇,此时乙还需要跑300 m才跑完第一圈.求甲、乙二人的速度及环形场地的周长.
应用4
环形跑道问题
探索新知
设乙的速度为x m/min,环形场地的周长为y m,
则甲的速度为2.5x m/min,
由题意,得
解得
2.5×150=375.
所以甲的速度为375 m/min,乙的速度为150 m/min,环形场地的周长为900 m.
解:
探索新知
6.A,B两镇相距12 km,甲从A镇、乙从B镇骑车同时出发,相向而行,设甲、乙行驶的速度分别为u km/h,υ km/h. ①出发后30 min相遇;②甲行驶的速度比乙行驶的速度快8 km/h,试根据题意,由条件列出方程组,并求解.
应用5
一般问题
由题意,得
解得
所以甲的速度为16 km/h,乙的速度为8 km/h.
解:
探索新知
同类变式
某人骑自行车从A地先以12 km/h的速度下坡后,再以9 km/h的速度走平路到B地,共用了55 min.回来时他以8 km/h的速度通过平路后,以4 km/h的速度上坡,从B地到A地共用了1.5 h.求A,B两地相距多少千米.
7.
探索新知
2
配套问题
题型
8. 某商场计划拨款9万元从厂家购进50台电冰箱,已知该厂家生产三种不同型号的电冰箱,出厂价分别为:甲种每台1 500元,乙种每台2 100元,丙种每台2 500元.
(1)该商场同时购进其中两种不同型号电冰箱共50台,用去9万元,请你研究一下商场的进货方案;
应用1
购物配套问题
探索新知
①设购进甲种电冰箱x台,购进乙种电冰箱y台,根据题意,得
解得
故第一种进货方案是购进甲、乙两种型号的电冰箱各25台.
解:
探索新知
②设购进甲种电冰箱x台,购进丙种电冰箱z台,
根据题意,得
解得
故第二种进货方案是购进甲种电冰箱35台,丙种电冰箱15台.
探索新知
③设购进乙种电冰箱y台,购进丙种电冰箱z台,
根据题意,得
解得
不合题意,舍去.故此种方案不可行.综上,商场共有两种进货方案,
方案一,购进甲、乙两种型号的电冰箱各25台;
方案二,购进甲种电冰箱35台,丙种电冰箱15台.
探索新知
(2)该商场销售一台甲种电冰箱可获利150元,销售一台乙种电冰箱可获利200元,销售一台丙种电冰箱可获利250元,在同时购进两种不同型号的方案中,为使销售时获利最多,应选择哪种进货方案?
第一种方案可获利150×25+200×25=8 750(元),
第二种方案可获利150×35+250×15=9 000(元).
因为8 750<9 000,所以应选择第二种进货方案,
即购进甲种电冰箱35台,丙种电冰箱15台.
解:
探索新知
9.食品安全是关乎民生的重要问题,在食品中添加过量的添加剂对人体健康有害,但适量的添加剂对人体无害而且有利于食品的储存和运输.为提高质量,做进一步研究.某饮料加工厂需生产A,B两种饮料共100瓶,需加入同种添加剂270 g,其中A饮料每瓶需加该添加剂2 g,B饮料每瓶需加该添加剂3 g,饮料加工厂生产了A,B两种饮料各多少瓶?
应用2
生产配套问题
探索新知
设饮料加工厂生产了A种饮料x瓶,B种饮料y瓶,根据题意,得
解得
所以饮料加工厂生产了A种饮料30瓶,B种饮料70瓶.
解:
探索新知
10.小颖参加课外兴趣活动时设计了一个圆柱体模型,现有150张白纸,一张白纸可做侧面16个或底面43个,一个侧面与两个底面配成一套模型,则用多少张纸制底面,多少张纸制侧面,才能正好配成整套模型?
设用x张纸制底面,y张纸制侧面,
则
解得
故用64张纸制底面,86张纸制侧面,才能正好配成整套模型.
解:
探索新知
某地生产一种绿色蔬菜,若在市场上直接销售,每吨的利润为1 000 元;经粗加工后销售,每吨的利润可达4 500 元;经精加工后销售,每吨的利润涨至7 500元.当地一家农工商公司收购这种蔬菜140 t,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16 t;如果进行精加工,每天可加工6 t,但两种加工方式不能同时进行.受季节条件的限制,公司必须在15天之内将这批蔬菜处理完毕,为此公司给出了三种加工方案:
11.
探索新知
方案1:将蔬菜全部进行粗加工;
方案2:尽可能多地对蔬菜进行精加工,没有来得及
加工的蔬菜在市场上直接销售;
方案3:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好在15天之内完成.
你认为选择哪种方案获利最多?
方案1获利为4 500×140=630 000(元).
方案2获利为7 500×6×15+1 000×(140-6×15)
=675 000+50 000=725 000(元).
解:
探索新知
方案3:设将x t蔬菜进行精加工,y t蔬菜进行粗加工.
根据题意,得
解得
所以方案3获利为7 500×60+4 500×80=810 000(元).
因为630 000<725 000<810 000,
所以选择方案3获利最多.
探索新知
12.某水果基地计划装运甲、乙、丙三种水果到外地销售(每辆汽车按规定满载,并且只装一种水果).下表为装运甲、乙、丙三种水果的质量及利润.
应用3
运输配套问题
甲 乙 丙
每辆汽车能装的质量/t 4 2 3
每吨水果可获利润/千元 5 7 4
探索新知
(1)用8辆汽车装运乙、丙两种水果共22 t到A地销售,问装运乙、丙两种水果的汽车各多少辆?
设装运乙、丙水果的汽车分别为x辆、y辆,
依题意,得
解得
所以装运乙水果的汽车有2辆,丙水果的汽车有6辆.
解:
探索新知
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72 t到B地销售(每种水果不少于一车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆(结果用m表示)
设装运乙、丙水果的汽车分别为a辆、b辆,
依题意,得
解得
所以装运乙水果的汽车是(m-12)辆,
丙水果的汽车是(32-2m)辆.
解:
探索新知
(3)在(2)问的基础上,如何安排装运可使水果基地获得最大利润?最大利润是多少?
设总利润为w千元,
w=5×4m+7×2(m-12)+4×3(32-2m)=10m+216.
因为
所以13≤m≤15.5.
因为m为正整数,所以m=13,14,15.
解:
探索新知
在w=10m+216中,w随m的增大而增大,
所以当m=15时,w最大=366.
所以当安排装运甲水果的汽车为15辆,装运乙水果的汽车为3辆,装运丙水果的汽车为2辆时,利润最大,最大利润为366千元.
求32-2m≥1中m的取值范围时,可先求出32-2m=1中m的值为15.5,所以只有m≤15.5时,32-2m≥1才成立.
点拨:
学以致用
小试牛刀
1.甲、乙二人练习跑步,如果甲让乙先跑10米,甲跑5秒就追上乙,如果甲让乙先跑2秒,那么甲跑4秒就追上乙,
则甲、乙两人的速度分别是__________________.
6米/秒,4米/秒
小试牛刀
2.某高速公路全长约126 km,一辆小汽车、一辆货车同时从巴中、广元两地相向开出,经过45分钟相遇.相遇时小汽车比货车多行6 km.设小汽车和货车的速度分别为x km/h,y km/h,则下列方程组正确的是( )
D
小试牛刀
3.一条船顺流航行,每小时行驶18 km;逆流航行,每小时行驶16 km.若设船在静水中的速度为x km/h,水流速度为y km/h,则列出的方程组为( )
B
小试牛刀
3.李明同学早上骑自行车上学,中途因道路施工步行一段路,到学校共用时15分钟.他骑自行车的平均速度是250米/分钟,步行的平均速度是80米/分钟,他家离学校的距离是2900米.如果他骑车和步行的时间分别为x,y分钟,列出的方程是( )
D
小试牛刀
4.达州景点真佛山的学生门票价格如下表所示:
某校八年级(1),(2)两个班去游览真佛山,其中(1)班人数较少,不足50人,(2)班人数较多,有50多人,两个班合起来超过100人.如果两个班都以班为单位分别购票,那么一共应付1240元;如果两个班联合起来,作为一个团体购票,那么只需付936元.
购票人数 1~50人 51~100人 100人以上
每张门票/元 13 11 9
小试牛刀
(1)列方程或方程组求出两个班各有多少学生;
(2)如果两个班不联合买票,那么八年级(1)班的学生非要买13元的票吗?你有什么省钱方式来帮他们买票吗?说说你的理由;
(3)你认为是否存在这样的可能:51~100人之间买票的钱数与100人以上买票的钱数相等?若有,是多少人与多少人买票钱数相等?
小试牛刀
(2)八年级(1)班的学生不一定非要买13元的票.(1)班可以买51人的票.
理由:由(1)可知八年级(1)班有48人,只需多买3张票,
即可按每张门票11元结算.51×11=561(元),48×13=624(元)>561元,
所以48人买51人的票可以更省钱
(3)存在.设人数在51~100人之间的人数为m,人数在100人以上的人数为n.假设存在买票钱数相等的状况,则满足11m=9n.因为m<100,n>100,所以符合题意的正整数解为m=90,n=110;m=99,n=121.即存在这样的可能,90人与110人,99人与121人买票钱数相等.
课堂小结
课堂小结
方法技能:
解决本节问题的关键是建立数学模型,常借助列表,
分析具体问题中的数量关系,使题目中的等量关系清晰浮现.
易错提示:
解题结果要符合题目的实际意义.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
