北师大版(新)八上-6.3 从统计图分析数据的集中趋势【优质课件】
文档属性
| 名称 | 北师大版(新)八上-6.3 从统计图分析数据的集中趋势【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览








文档简介
(共40张PPT)
6.3 从统计图分析数据
的集中趋势
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
复习回顾
如何确定一组数据的中位数和众数?
新课精讲
探索新知
1
知识点
从折线统计图中获取数据信息
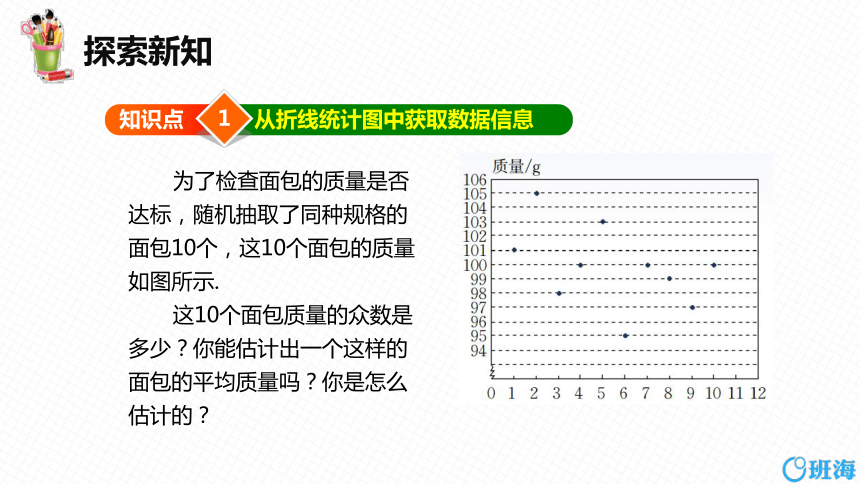
为了检查面包的质量是否达标,随机抽取了同种规格的面包10个,这10个面包的质量如图所示.
这10个面包质量的众数是多少?你能估计出一个这样的面包的平均质量吗?你是怎么估计的?
探索新知
因为折线统计图具有能够显示数据的变化趋势,反映事物的变化情况的特点,所以利用折线统计图比较容易看出数据的众数,也比较容易求出数据的中位数和平均数.
探索新知
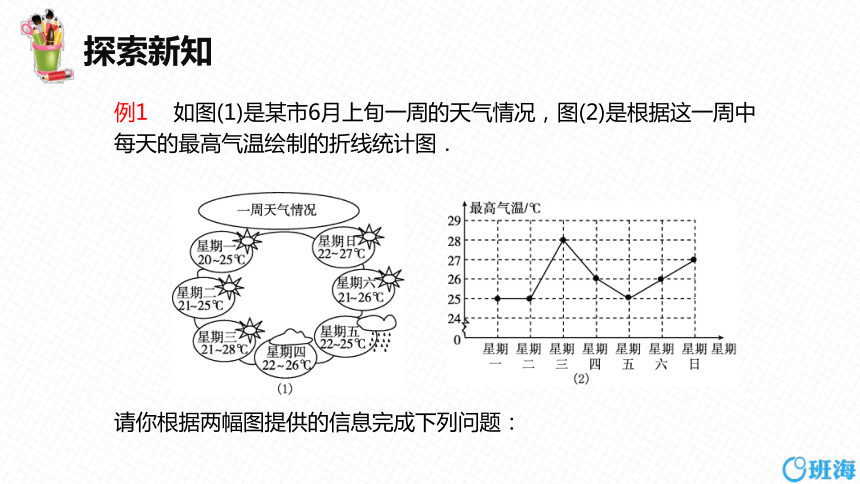
例1 如图(1)是某市6月上旬一周的天气情况,图(2)是根据这一周中每天的最高气温绘制的折线统计图.
请你根据两幅图提供的信息完成下列问题:
探索新知
(1)这一周中温差最大的一天是星期________;
(2)这一周中每天最高气温的众数是______℃,中位数是______℃, 平均数是________℃;
(3)这两幅图各有特点,而关于折线统计图的优点,下列四句话中描
述最贴切的一句是________.(填序号)
①可以清楚地告诉我们每天天气情况;
②可以清楚地告诉我们各部分数量占总量的百分比的情况;
③可以直观地告诉我们这一周每天最高气温的变化情况;
④可以清楚地告诉我们这一周每天气温的总体情况.
三
25
26
26
③
典题精讲
1
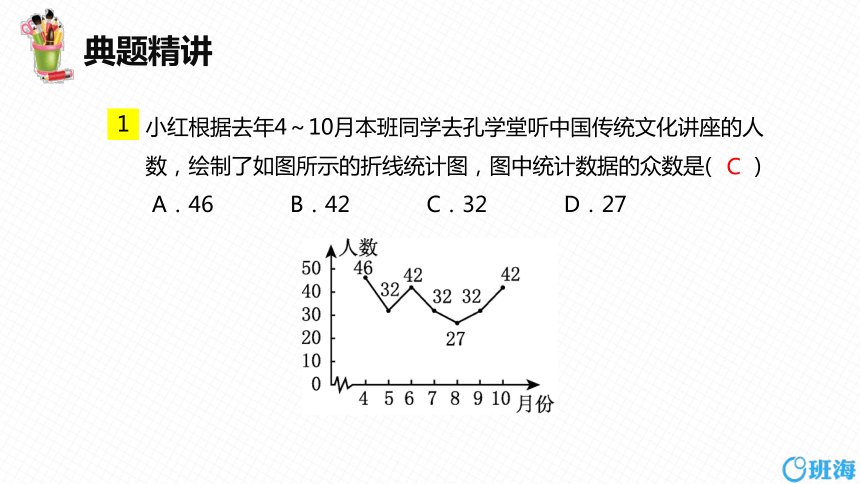
小红根据去年4~10月本班同学去孔学堂听中国传统文化讲座的人数,绘制了如图所示的折线统计图,图中统计数据的众数是( )
A.46 B.42 C.32 D.27
C
探索新知
2
知识点
从条形统计图(频数直方图)中获取数据信息
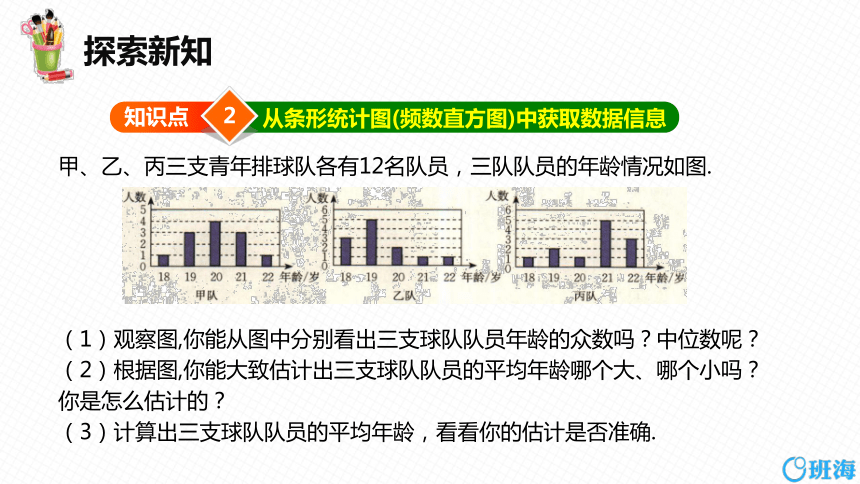
甲、乙、丙三支青年排球队各有12名队员,三队队员的年龄情况如图.
(1)观察图,你能从图中分别看出三支球队队员年龄的众数吗?中位数呢?
(2)根据图,你能大致估计出三支球队队员的平均年龄哪个大、哪个小吗?你是怎么估计的?
(3)计算出三支球队队员的平均年龄,看看你的估计是否准确.
探索新知
因为条形统计图能清楚地表示出数量的多少,所以利用条形统计图更容易看出数据的众数、中位数,利用加权平均数的求法可以求出数据的平均数.
探索新知
例2 某市初中毕业生升学体育集中测试项目包括体能(耐力)类项目和速度(跳跃、力量、技能)类项目.体能类项目从游泳和中长跑中任选一项,速度类项目从立定跳远、50米跑等6项中任选一项.某校九年级共有200名女生在速度类项目中选择了立定跳远,现从这200名女生中随机抽取10名女生进行测试,如图是她们立定跳远距离的条形统计图.(另附:九年级女生立定跳远的计分标准)
10名女生立定跳远距离条形统计图
探索新知
九年级女生立定跳远计分标准
立定跳远距离/cm 197 189 181 173 …
得分/分 10 9 8 7 …
注:不到上限,则按下限计分,满分为10分.
(1)求这10名女生在本次测试中,立定跳远距离的中位数,立定跳远得分的众数和平均数;
(2)请你估计该校选择立定跳远的200名女生中得满分的人数.
导引:(1)题根据中位数、众数和平均数的概念解决.(2)题易知10名女生中得满分的有6人,所以估计200名女生中得满分的人数是200×
探索新知
解:(1)立定跳远距离的中位数为
根据计分标准,这10名女生的立定跳远得分分别是
(单位:分):7,9,10,10,10,10,8,10,10,
9,所以立定跳远得分的众数是10分,立定跳远得
分的平均数是9.3分.
(2)因为10名女生中有6名得满分,所以估计200名女生
中得满分的人数是200×
探索新知
总 结
统计来源于生活,应用对数据的统计思想来理解现实生活中的一些事物,是近年来中考考查的热点.图表信息题主要考查学生的识图能力.
典题精讲
某射击小组有20人,教练根据他们某次射击的数据绘制如图所示的统计图,则这组数据的众数和中位数分别是( )
A.7,7
B.8,7.5
C.7,7.5
D.8,6
1
C
典题精讲
为了了解初三学生的体育锻炼时间,小华调查了某班46名同学一周参加体育锻炼的情况,并把它绘制成条形统计图(如图),那么关于该班46名同学一周参加体育锻炼时间的说法错误的是( )
A.众数是9 h
B.中位数是9 h
C.平均数大约是9 h
D.锻炼时间不高于9 h的有14人
2
D
探索新知
3
知识点
扇形统计图
做一做
小明调查了班级里20名同学
本学期计划购买课外书的花费情况,
并将结果绘制成了右图.
(1)在这20名同学中,本学期计划
购买课外书的花费的众数是多少?
(2)计算这20名同学计划购买课外书的平均花费.你是怎么计算的
探索新知
想一想
在上面的问题中,如果不知道调查的总人数,你还能求平均数吗
因为扇形统计图能看出部分在总体中所占的百分比,所以利用扇形统计图更容易看出数据的众数;利用加权平均数的求法可以求出数据的平均数.
探索新知
例3 某地连续统计了 10天日最高
气温,并绘制成如图所示的扇形统计图.
(1)这10天中,日最高气温的众数是多少?
(2)计算这10天日最高气温的平均值.
解:(1)根据扇形统计图,35℃占的比例最大,因此日平均气温的众数是35℃;
(2)这10天日最高气温的平均值是:32×10%+33×20%+34×20%+35×30%+36×20%=34.3(℃).
探索新知
总 结
从统计图中我们可以获取有用的数据信息,通过计算可以得到这组数据的平均数;通过数各个数据出现的次数可以确定这组数据的众数;中位数是把这组数据按大小顺序排列后处于最中间位置的一个数据.
典题精讲
1
如图是某校学生参加课外兴趣小组的人数占总人数比例的统计图,则参加人数最多的课外兴趣小组是( )
A.音乐组
B.美术组
C.体育组
D.科技组
C
典题精讲
从某校八年级中随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分,5分.将测量的结果制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些学生分数的中位数是( )
A.1分
B.2分
C.3分
D.4分
2
C
学以致用
小试牛刀
1 .在学校演讲比赛中,10名选手的成绩统计图如图所示,则这10名选手成绩的众数是( )
A.95分
B.90分
C.85分
D.80分
B
小试牛刀
2 .端午节期间,某市一周每天最高气温(单位:℃)情况如图所示,则这组表示最高气温数据的中位数是( )
A.22
B.24
C.25
D.27
B
小试牛刀
3 .华明中学围绕“珍爱生命,远离毒品”主题,组织师生到当地戒毒所开展相关问题的问卷调查活动,其中“初次吸毒时的年龄”在17至21岁的统计结果如图所示,则这些年龄的众数是( )
A.18岁
B.19岁
C.20岁
D.21岁
C
小试牛刀
4.如图是某班45名同学爱心捐款额的频数直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一组是( )
A.5~10元
B.10~15元
C.15~20元
D.20~25元
C
小试牛刀
5 .某校八年级(3)班50名学生自发组织献爱心捐款活动.班长将捐款情况进行了统计,并绘制成了统计图(如图).根据图中提供的信息,捐款金额的众数是( )
A.20元
B.30元
C.50元
D.100元
B
小试牛刀
6 .甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图(如图)和统计表(如下).
甲组12户家庭用水量统计表
用水量(吨) 4 5 6 9
户数 4 5 2 1
小试牛刀
比较5月份两组家庭用水量的中位数,下列说法正确的是( )
A.甲组比乙组大
B.甲、乙两组相同
C.乙组比甲组大
D.无法判断
B
小试牛刀
7.某校九年级有24个班,共1 000名学生,他们参加了一次数学测试,学校统计了所有学生的成绩,得到如图所示的统计图.
(1)求该校九年级学生本次数学测试成绩的平均数;
(1)根据题意得(80×1 000×60%+82.5×1 000×40%)÷1 000=81(分),所以该校九年级学生本次数学测试成绩的平均数是81分.
解:
小试牛刀
(2)下列关于本次数学测试说法正确的是( )
A.九年级学生成绩的众数与平均数相等
B.九年级学生成绩的中位数与平均数相等
C.随机抽取一个班,该班学生成绩的平均数等于九年级学生成绩的平均数
D.随机抽取300名学生,可以用他们成绩的平均数估计九年级学生成绩的平均数
D
小试牛刀
8.某校为了进一步改善本校七年级的数学教学,提高学生学习数学的兴趣,校教务处在七年级所有班级中,每班随机抽取了6名学生,并对他们的数学学习情况进行了问卷调查.我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A.非常喜欢”、“B.比较喜欢”、“C.不太喜欢”、“D.很不喜欢”,针对这个题目,问卷时要求每名被调查的学生必须从中选一项且只能选一项)结果进行了统计,现将统计结果绘制成如图所示两幅不完整的统计图.
小试牛刀
请你根据以上提供的信息,解答下列问题:
(1)补全上面的条形统计图和扇形统计图;
(2)所抽取学生对数学学习喜欢程度的众数是_________;
(3)若该校七年级共有960名学生,请你估算该年级学生中对数学学习“不太喜欢”的约有多少名.
比较喜欢
小试牛刀
(1)由题意可得,
调查的学生有30÷25%=120(名),
选B的学生有120-18-30-6=66(名),
B所占的百分比是66÷120×100%=55%,
D所占的百分比是6÷120×100%=5%,
故补全的条形统计图与扇形统计图如图所示:
(3)960×25%= 240(名).
答:该年级学生中对数学学习“不太喜欢”的约有240名.
解:
课堂小结
课堂小结
三种统计图的优缺点:
(1)因为折线统计图具有能够显示数据的变化趋势,反映事物的变化情况的特点,所以利用折线统计图比较容易看出数据的众数,也比较容易求出数据的中位数和平均数;
(2)因为条形统计图能清楚地表示出数量的多少,所以利用条形统计图更容易看出数据的众数、中位数,利用加权平均数的求法可以求出数据的平均数;
(3)因为扇形统计图能看出部分在总体中所占的百分比,所以利用扇形统计图更容易看出数据的众数;利用加权平均数的求法可 以求出数据的平均数.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
6.3 从统计图分析数据
的集中趋势
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
复习回顾
如何确定一组数据的中位数和众数?
新课精讲
探索新知
1
知识点
从折线统计图中获取数据信息
为了检查面包的质量是否达标,随机抽取了同种规格的面包10个,这10个面包的质量如图所示.
这10个面包质量的众数是多少?你能估计出一个这样的面包的平均质量吗?你是怎么估计的?
探索新知
因为折线统计图具有能够显示数据的变化趋势,反映事物的变化情况的特点,所以利用折线统计图比较容易看出数据的众数,也比较容易求出数据的中位数和平均数.
探索新知
例1 如图(1)是某市6月上旬一周的天气情况,图(2)是根据这一周中每天的最高气温绘制的折线统计图.
请你根据两幅图提供的信息完成下列问题:
探索新知
(1)这一周中温差最大的一天是星期________;
(2)这一周中每天最高气温的众数是______℃,中位数是______℃, 平均数是________℃;
(3)这两幅图各有特点,而关于折线统计图的优点,下列四句话中描
述最贴切的一句是________.(填序号)
①可以清楚地告诉我们每天天气情况;
②可以清楚地告诉我们各部分数量占总量的百分比的情况;
③可以直观地告诉我们这一周每天最高气温的变化情况;
④可以清楚地告诉我们这一周每天气温的总体情况.
三
25
26
26
③
典题精讲
1
小红根据去年4~10月本班同学去孔学堂听中国传统文化讲座的人数,绘制了如图所示的折线统计图,图中统计数据的众数是( )
A.46 B.42 C.32 D.27
C
探索新知
2
知识点
从条形统计图(频数直方图)中获取数据信息
甲、乙、丙三支青年排球队各有12名队员,三队队员的年龄情况如图.
(1)观察图,你能从图中分别看出三支球队队员年龄的众数吗?中位数呢?
(2)根据图,你能大致估计出三支球队队员的平均年龄哪个大、哪个小吗?你是怎么估计的?
(3)计算出三支球队队员的平均年龄,看看你的估计是否准确.
探索新知
因为条形统计图能清楚地表示出数量的多少,所以利用条形统计图更容易看出数据的众数、中位数,利用加权平均数的求法可以求出数据的平均数.
探索新知
例2 某市初中毕业生升学体育集中测试项目包括体能(耐力)类项目和速度(跳跃、力量、技能)类项目.体能类项目从游泳和中长跑中任选一项,速度类项目从立定跳远、50米跑等6项中任选一项.某校九年级共有200名女生在速度类项目中选择了立定跳远,现从这200名女生中随机抽取10名女生进行测试,如图是她们立定跳远距离的条形统计图.(另附:九年级女生立定跳远的计分标准)
10名女生立定跳远距离条形统计图
探索新知
九年级女生立定跳远计分标准
立定跳远距离/cm 197 189 181 173 …
得分/分 10 9 8 7 …
注:不到上限,则按下限计分,满分为10分.
(1)求这10名女生在本次测试中,立定跳远距离的中位数,立定跳远得分的众数和平均数;
(2)请你估计该校选择立定跳远的200名女生中得满分的人数.
导引:(1)题根据中位数、众数和平均数的概念解决.(2)题易知10名女生中得满分的有6人,所以估计200名女生中得满分的人数是200×
探索新知
解:(1)立定跳远距离的中位数为
根据计分标准,这10名女生的立定跳远得分分别是
(单位:分):7,9,10,10,10,10,8,10,10,
9,所以立定跳远得分的众数是10分,立定跳远得
分的平均数是9.3分.
(2)因为10名女生中有6名得满分,所以估计200名女生
中得满分的人数是200×
探索新知
总 结
统计来源于生活,应用对数据的统计思想来理解现实生活中的一些事物,是近年来中考考查的热点.图表信息题主要考查学生的识图能力.
典题精讲
某射击小组有20人,教练根据他们某次射击的数据绘制如图所示的统计图,则这组数据的众数和中位数分别是( )
A.7,7
B.8,7.5
C.7,7.5
D.8,6
1
C
典题精讲
为了了解初三学生的体育锻炼时间,小华调查了某班46名同学一周参加体育锻炼的情况,并把它绘制成条形统计图(如图),那么关于该班46名同学一周参加体育锻炼时间的说法错误的是( )
A.众数是9 h
B.中位数是9 h
C.平均数大约是9 h
D.锻炼时间不高于9 h的有14人
2
D
探索新知
3
知识点
扇形统计图
做一做
小明调查了班级里20名同学
本学期计划购买课外书的花费情况,
并将结果绘制成了右图.
(1)在这20名同学中,本学期计划
购买课外书的花费的众数是多少?
(2)计算这20名同学计划购买课外书的平均花费.你是怎么计算的
探索新知
想一想
在上面的问题中,如果不知道调查的总人数,你还能求平均数吗
因为扇形统计图能看出部分在总体中所占的百分比,所以利用扇形统计图更容易看出数据的众数;利用加权平均数的求法可以求出数据的平均数.
探索新知
例3 某地连续统计了 10天日最高
气温,并绘制成如图所示的扇形统计图.
(1)这10天中,日最高气温的众数是多少?
(2)计算这10天日最高气温的平均值.
解:(1)根据扇形统计图,35℃占的比例最大,因此日平均气温的众数是35℃;
(2)这10天日最高气温的平均值是:32×10%+33×20%+34×20%+35×30%+36×20%=34.3(℃).
探索新知
总 结
从统计图中我们可以获取有用的数据信息,通过计算可以得到这组数据的平均数;通过数各个数据出现的次数可以确定这组数据的众数;中位数是把这组数据按大小顺序排列后处于最中间位置的一个数据.
典题精讲
1
如图是某校学生参加课外兴趣小组的人数占总人数比例的统计图,则参加人数最多的课外兴趣小组是( )
A.音乐组
B.美术组
C.体育组
D.科技组
C
典题精讲
从某校八年级中随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分,5分.将测量的结果制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些学生分数的中位数是( )
A.1分
B.2分
C.3分
D.4分
2
C
学以致用
小试牛刀
1 .在学校演讲比赛中,10名选手的成绩统计图如图所示,则这10名选手成绩的众数是( )
A.95分
B.90分
C.85分
D.80分
B
小试牛刀
2 .端午节期间,某市一周每天最高气温(单位:℃)情况如图所示,则这组表示最高气温数据的中位数是( )
A.22
B.24
C.25
D.27
B
小试牛刀
3 .华明中学围绕“珍爱生命,远离毒品”主题,组织师生到当地戒毒所开展相关问题的问卷调查活动,其中“初次吸毒时的年龄”在17至21岁的统计结果如图所示,则这些年龄的众数是( )
A.18岁
B.19岁
C.20岁
D.21岁
C
小试牛刀
4.如图是某班45名同学爱心捐款额的频数直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一组是( )
A.5~10元
B.10~15元
C.15~20元
D.20~25元
C
小试牛刀
5 .某校八年级(3)班50名学生自发组织献爱心捐款活动.班长将捐款情况进行了统计,并绘制成了统计图(如图).根据图中提供的信息,捐款金额的众数是( )
A.20元
B.30元
C.50元
D.100元
B
小试牛刀
6 .甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图(如图)和统计表(如下).
甲组12户家庭用水量统计表
用水量(吨) 4 5 6 9
户数 4 5 2 1
小试牛刀
比较5月份两组家庭用水量的中位数,下列说法正确的是( )
A.甲组比乙组大
B.甲、乙两组相同
C.乙组比甲组大
D.无法判断
B
小试牛刀
7.某校九年级有24个班,共1 000名学生,他们参加了一次数学测试,学校统计了所有学生的成绩,得到如图所示的统计图.
(1)求该校九年级学生本次数学测试成绩的平均数;
(1)根据题意得(80×1 000×60%+82.5×1 000×40%)÷1 000=81(分),所以该校九年级学生本次数学测试成绩的平均数是81分.
解:
小试牛刀
(2)下列关于本次数学测试说法正确的是( )
A.九年级学生成绩的众数与平均数相等
B.九年级学生成绩的中位数与平均数相等
C.随机抽取一个班,该班学生成绩的平均数等于九年级学生成绩的平均数
D.随机抽取300名学生,可以用他们成绩的平均数估计九年级学生成绩的平均数
D
小试牛刀
8.某校为了进一步改善本校七年级的数学教学,提高学生学习数学的兴趣,校教务处在七年级所有班级中,每班随机抽取了6名学生,并对他们的数学学习情况进行了问卷调查.我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A.非常喜欢”、“B.比较喜欢”、“C.不太喜欢”、“D.很不喜欢”,针对这个题目,问卷时要求每名被调查的学生必须从中选一项且只能选一项)结果进行了统计,现将统计结果绘制成如图所示两幅不完整的统计图.
小试牛刀
请你根据以上提供的信息,解答下列问题:
(1)补全上面的条形统计图和扇形统计图;
(2)所抽取学生对数学学习喜欢程度的众数是_________;
(3)若该校七年级共有960名学生,请你估算该年级学生中对数学学习“不太喜欢”的约有多少名.
比较喜欢
小试牛刀
(1)由题意可得,
调查的学生有30÷25%=120(名),
选B的学生有120-18-30-6=66(名),
B所占的百分比是66÷120×100%=55%,
D所占的百分比是6÷120×100%=5%,
故补全的条形统计图与扇形统计图如图所示:
(3)960×25%= 240(名).
答:该年级学生中对数学学习“不太喜欢”的约有240名.
解:
课堂小结
课堂小结
三种统计图的优缺点:
(1)因为折线统计图具有能够显示数据的变化趋势,反映事物的变化情况的特点,所以利用折线统计图比较容易看出数据的众数,也比较容易求出数据的中位数和平均数;
(2)因为条形统计图能清楚地表示出数量的多少,所以利用条形统计图更容易看出数据的众数、中位数,利用加权平均数的求法可以求出数据的平均数;
(3)因为扇形统计图能看出部分在总体中所占的百分比,所以利用扇形统计图更容易看出数据的众数;利用加权平均数的求法可 以求出数据的平均数.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
