北师大版(新)八上-1.1 探索勾股定理 第二课时【优质课件】
文档属性
| 名称 | 北师大版(新)八上-1.1 探索勾股定理 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览







文档简介
(共34张PPT)
1.1 探索勾股定理
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
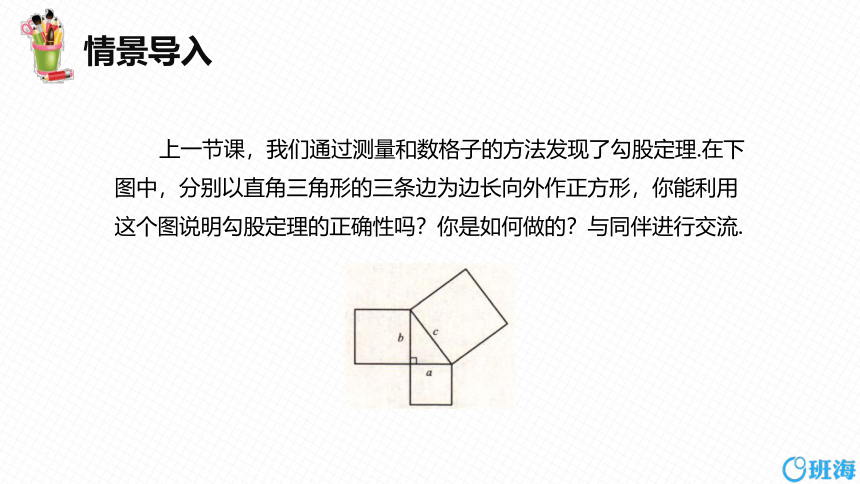
上一节课,我们通过测量和数格子的方法发现了勾股定理.在下图中,分别以直角三角形的三条边为边长向外作正方形,你能利用这个图说明勾股定理的正确性吗?你是如何做的?与同伴进行交流.
新课精讲
探索新知
1
知识点
勾股定理的验证
做一做
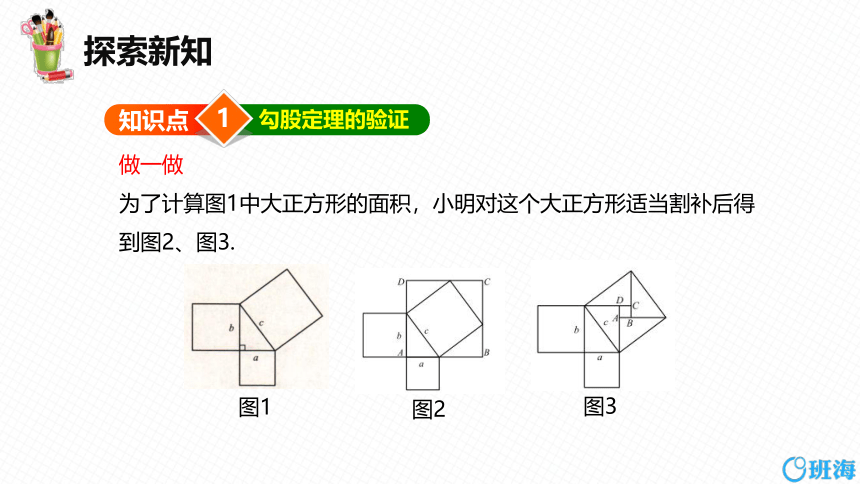
为了计算图1中大正方形的面积,小明对这个大正方形适当割补后得到图2、图3.
图1
图2
图3
探索新知
(1)将所有三角形和正方形的面积用a,b,c的关系式表示出来;
(2) 图2、图3中正方形ABCD的面积分别是多少?你们有哪些表示方式?与同伴进行交流.
(3)你能分别利用图2、图3验证勾股定理吗?
探索新知
1.常用方法:通过拼图法利用求面积来验证.这种方法是以数形转换为指导思想,图形拼补为手段,以各部分面积之间的关系为依据而达到目的的.
2.用拼图法验证勾股定理的思路:
(1)图形经过割补、拼接后,只要没有重叠,没有空隙,面积不会改变;
(2)根据同一种图形的面积的不同表示方法列出等式;
(3)利用等式性质验证结论成立,即拼出图形→写出图形面积的表达式→找出等量关系→恒等变形→推导结论.
探索新知
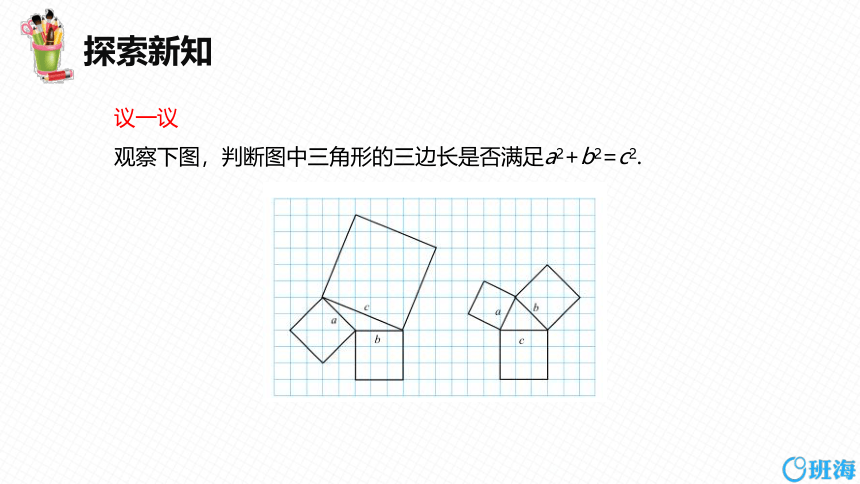
议一议
观察下图,判断图中三角形的三边长是否满足a2+b2=c2.
探索新知
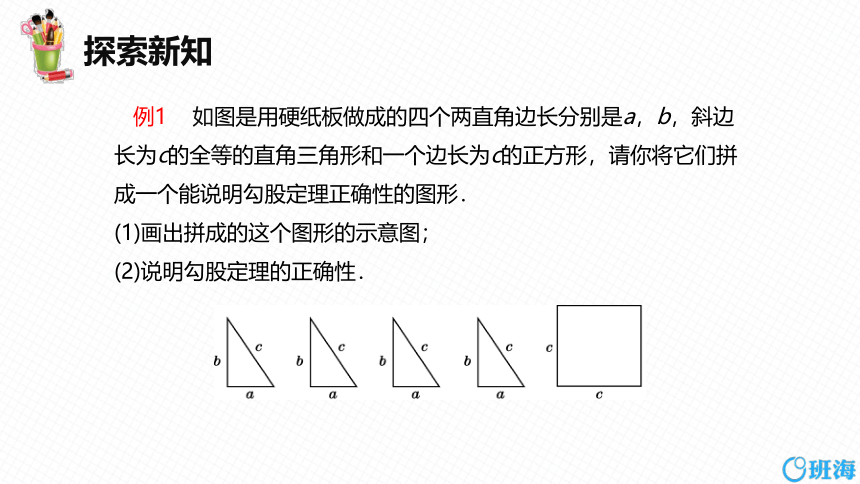
例1 如图是用硬纸板做成的四个两直角边长分别是a,b,斜边长为c的全等的直角三角形和一个边长为c的正方形,请你将它们拼成一个能说明勾股定理正确性的图形.
(1)画出拼成的这个图形的示意图;
(2)说明勾股定理的正确性.
探索新知
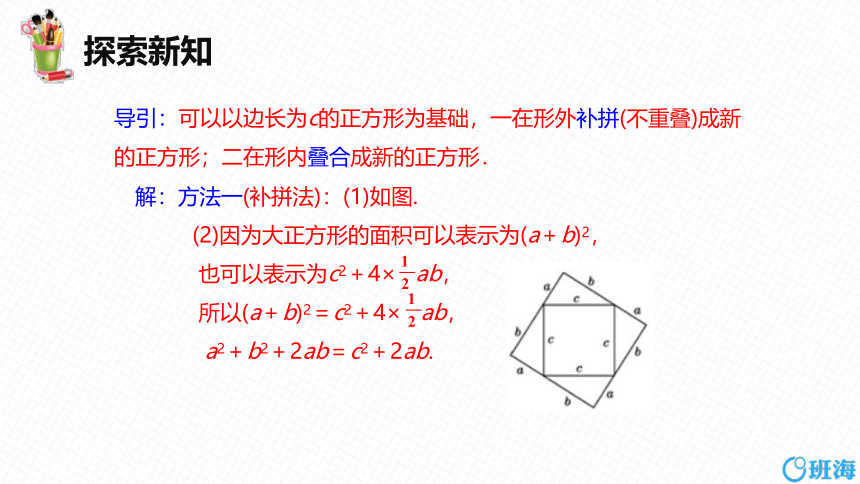
导引:可以以边长为c的正方形为基础,一在形外补拼(不重叠)成新的正方形;二在形内叠合成新的正方形.
解:方法一(补拼法):(1)如图.
(2)因为大正方形的面积可以表示为(a+b)2,
也可以表示为c2+4× ab,
所以(a+b)2=c2+4× ab,
a2+b2+2ab=c2+2ab.
探索新知
所以a2+b2=c2,
即直角三角形两直角边的平方和 等于斜边的平方.
方法二(叠合法):(1)如图.
(2)因为大正方形的面积可以表示为c2,
也可以表示为 ab×4+(b-a)2,
所以c2= ab×4+(b-a)2,c2=2ab+b2-2ab+a2.
所以a2+b2=c2,
即直角三角形两直角边的平方和等于斜边的平方.
探索新知
总 结
勾股定理的验证主要是通过拼图法利用面积的关系完成的,拼图又常以补拼法和叠合法两种方式拼图,补拼是要无重叠,叠合是要无空隙;而用面积法验证的关键是要找到一些特殊图形(如直角三角形、正方形、梯形)的面积之和等于整个图形的面积,从而达到验证的目的.
典题精讲
用四个边长均为a,b,c的直角三角板,拼成如 图所示的图形,则下列结论中正确的是( )
A.c2=a2+b2 B.c2=a2+2ab+b2
C.c2=a2-2ab+b2 D.c2=(a+b)2
A
探索新知
2
知识点
勾股定理的应用
例2 我方侦察员小王在距离东西向公路400m处侦察,发现一 辆敌方汽车在公路上疾驰.他赶紧拿出红外测距仪,测得汽车与他相距400m,10s后,汽车与他相距500m,你能帮小王计算敌方汽车的速度吗?
分析:根据题意,可以画出右图,
其中点A表示小王所在位置,
点C、点B表示两个时刻敌方汽车的位置.
探索新知
由于小王距离公路400m,因此∠C是直角,这样就可以由勾股定理来解决这个问题了.
解:由勾股定理,可以得到AB2=BC2+AC2,
也就是5002=BC2+4002,
所以BC=300.敌方汽车10s行驶了300m,
那么它1h行驶的距离为300×6×60=108000(m),
即它行驶的速度为108km/h.
探索新知
1. 勾股定理是一个重要的数学定理,它将图形(直角三角形)与数量关系(三边关系)有机结合起来;在几何及日常生活中都有着广泛的应用.
2.运用勾股定理进行计算分三步:第一步:注意应用的前提,即看是不是直角三角形;第二步:分清求解的对象,即看是求直角边长,还是斜边长或者两种均有可能;第三步:运用勾股定理进行计算.
探索新知
例3 〈实际应用题〉两棵树之间的距离为8 m,两棵树的高度分别是8 m,2 m,一只小鸟从一棵树的树顶飞到另一棵树的树顶,这只小鸟至少要飞多少米?
导引:先根据题意画出图形,然后添加辅助线,构造直角三角形,再利用勾股定理求解.
探索新知
解:根据题意画出示意图,如图所示,
两棵树的高度分别为AB=8 m,CD=2 m,
两棵树之间的距离BD=8 m,
过点C作CE⊥AB,垂足为E,连接AC.
则BE=CD=2 m,EC=BD=8 m,
AE=AB-BE=8-2=6(m).
在Rt△ACE中,由勾股定理,得AC2=AE2+EC2,
即AC2=62+82=100,所以AC=10 m.
答:这只小鸟至少要飞10 m.
典题精讲
如图,一个长为2.5 m的梯子,一端放在离墙脚1.5 m处,另一端靠墙,则梯子顶端距离墙脚( )
A.0.2 m B.0.4 m C.2 m D.4 m
C
典题精讲
2 如图,有两棵树,一棵高10 m,另一棵高4 m,两树相距8 m,一只小鸟从一棵树的树顶飞到另一棵树的树顶,小鸟至少飞行( )
A.8 m B.10 m C.12 m D.14 m
B
学以致用
小试牛刀
1.勾股定理的验证方法很多,主要是用________法说明,要注意两点:(1)通过割补、拼摆,用相同的直角三角形得到一个图形;
面积
(2)根据拼成的图形得到一个________关系式,通过恒等变形即可得到勾股定理.
例:图①反映的面积关系式为
___________________________;
图②反映的面积关系式为___________________________.
面积
小试牛刀
2.在Rt△ABC中,a,b是两直角边,c为斜边,如果已知a,b,那么c2=________;如果已知a,c,那么b2=________;如果已知b,c,那么a2=_______.当不能直接运用勾股定理求线段长度时,则设所求线段的长度为x,并选择一个合适的直角三角形,根据勾股定理,列出含________的方程.
a2+b2
c2-a2
c2-b2
x
A.S△EDA=S△CEB
B.S△EDA+S△CEB=S△CDE
C.S四边形CDAE=S四边形CDEB
D.S△EDA+S△CDE+S△CEB=S四边形ABCD
小试牛刀
3.历史上对勾股定理的一种验证方法采用了如图所示的图形,其中两个全等直角三角形的边AE,EB在一条直线上,其中用到的面积相等的关系式是( )
D
小试牛刀
4.九章算术》中的“折竹抵地”问题(如图):今有竹高一丈,末折抵地,去根六尺,问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )
A.x2-6=(10-x)2
B.x2-62=(10-x)2
C.x2+6=(10-x)2
D.x2+62=(10-x)2
D
小试牛刀
5.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙脚的距离为0.7 m,顶端距离地面2.4 m.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2 m,则小巷的宽度为( )
A.0.7 m B.1.5 m
C.2.2 m D.2.4 m
C
小试牛刀
6.如图,在正方形网格中,每个小正方形的边长均为1,△ABC在网格中,顶点均为格点.求点A到直线BC的距离.
S△ABC=4×5- ×2×5- ×2×2- ×3×4=7.
因为BC2=32+42=52,所以BC=5.
设点A到直线BC的距离为h,
因为S△ABC= BC h,
所以 ×5h=7,所以h= .
故点A到直线BC的距离是 .
小试牛刀
7.如图,AD是△ABC的中线,试说明AB2+AC2=2(AD2+CD2).
过点A作AE⊥BC于点E.
在Rt△ABE,Rt△ACE和Rt△ADE中,由勾股定理得
AB2=AE2+BE2,AC2=AE2+EC2,AE2=AD2-DE2,
因为AD是△ABC的中线,所以BD=CD.所以AB2+AC2=2AD2+2CD2,即AB2+AC2=2(AD2+CD2).
所以AB2+AC2=2AE2+BE2+EC2=2(AD2-DE2)+(BD-DE)2+(CD+DE)2=2AD2-2DE2+BD2-2BD DE+DE2+CD2+2CD DE+DE2
=2AD2+BD2+CD2-2BD DE+2CD DE.
小试牛刀
8.如图,在一棵树的10 m高的B处有两只猴子,其中一只猴子爬下树,走到离树20 m处的池塘A处,另一只猴子爬到树顶D后直接跃向池塘A处(假设它跃过的路线为直线).如果两只猴子所经过的路程相等,求这棵树的高.
【思路点拨】通过设未知数,根据两只猴子经过的路程相等表示出AD的长度,再利用勾股定理列方程求解.
小试牛刀
解:
设BD=x m,由题意知BC+AC=BD+AD,
所以AD=(30-x)m.
所以(10+x)2+202=(30-x)2. 解得x=5.
所以x+10=15,即这棵树的高为15 m.
课堂小结
课堂小结
用拼图验证勾股定理的方法:首先通过拼图找出面积之间的相等关系,再由面积之间的相等关系结合图形进行代数变形即可推导出勾股定理.
它一般都经过以下几个步骤:拼出图形→写出图形面积的表达式→找出相等关系→恒等变形→导出勾股定理.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
1.1 探索勾股定理
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
上一节课,我们通过测量和数格子的方法发现了勾股定理.在下图中,分别以直角三角形的三条边为边长向外作正方形,你能利用这个图说明勾股定理的正确性吗?你是如何做的?与同伴进行交流.
新课精讲
探索新知
1
知识点
勾股定理的验证
做一做
为了计算图1中大正方形的面积,小明对这个大正方形适当割补后得到图2、图3.
图1
图2
图3
探索新知
(1)将所有三角形和正方形的面积用a,b,c的关系式表示出来;
(2) 图2、图3中正方形ABCD的面积分别是多少?你们有哪些表示方式?与同伴进行交流.
(3)你能分别利用图2、图3验证勾股定理吗?
探索新知
1.常用方法:通过拼图法利用求面积来验证.这种方法是以数形转换为指导思想,图形拼补为手段,以各部分面积之间的关系为依据而达到目的的.
2.用拼图法验证勾股定理的思路:
(1)图形经过割补、拼接后,只要没有重叠,没有空隙,面积不会改变;
(2)根据同一种图形的面积的不同表示方法列出等式;
(3)利用等式性质验证结论成立,即拼出图形→写出图形面积的表达式→找出等量关系→恒等变形→推导结论.
探索新知
议一议
观察下图,判断图中三角形的三边长是否满足a2+b2=c2.
探索新知
例1 如图是用硬纸板做成的四个两直角边长分别是a,b,斜边长为c的全等的直角三角形和一个边长为c的正方形,请你将它们拼成一个能说明勾股定理正确性的图形.
(1)画出拼成的这个图形的示意图;
(2)说明勾股定理的正确性.
探索新知
导引:可以以边长为c的正方形为基础,一在形外补拼(不重叠)成新的正方形;二在形内叠合成新的正方形.
解:方法一(补拼法):(1)如图.
(2)因为大正方形的面积可以表示为(a+b)2,
也可以表示为c2+4× ab,
所以(a+b)2=c2+4× ab,
a2+b2+2ab=c2+2ab.
探索新知
所以a2+b2=c2,
即直角三角形两直角边的平方和 等于斜边的平方.
方法二(叠合法):(1)如图.
(2)因为大正方形的面积可以表示为c2,
也可以表示为 ab×4+(b-a)2,
所以c2= ab×4+(b-a)2,c2=2ab+b2-2ab+a2.
所以a2+b2=c2,
即直角三角形两直角边的平方和等于斜边的平方.
探索新知
总 结
勾股定理的验证主要是通过拼图法利用面积的关系完成的,拼图又常以补拼法和叠合法两种方式拼图,补拼是要无重叠,叠合是要无空隙;而用面积法验证的关键是要找到一些特殊图形(如直角三角形、正方形、梯形)的面积之和等于整个图形的面积,从而达到验证的目的.
典题精讲
用四个边长均为a,b,c的直角三角板,拼成如 图所示的图形,则下列结论中正确的是( )
A.c2=a2+b2 B.c2=a2+2ab+b2
C.c2=a2-2ab+b2 D.c2=(a+b)2
A
探索新知
2
知识点
勾股定理的应用
例2 我方侦察员小王在距离东西向公路400m处侦察,发现一 辆敌方汽车在公路上疾驰.他赶紧拿出红外测距仪,测得汽车与他相距400m,10s后,汽车与他相距500m,你能帮小王计算敌方汽车的速度吗?
分析:根据题意,可以画出右图,
其中点A表示小王所在位置,
点C、点B表示两个时刻敌方汽车的位置.
探索新知
由于小王距离公路400m,因此∠C是直角,这样就可以由勾股定理来解决这个问题了.
解:由勾股定理,可以得到AB2=BC2+AC2,
也就是5002=BC2+4002,
所以BC=300.敌方汽车10s行驶了300m,
那么它1h行驶的距离为300×6×60=108000(m),
即它行驶的速度为108km/h.
探索新知
1. 勾股定理是一个重要的数学定理,它将图形(直角三角形)与数量关系(三边关系)有机结合起来;在几何及日常生活中都有着广泛的应用.
2.运用勾股定理进行计算分三步:第一步:注意应用的前提,即看是不是直角三角形;第二步:分清求解的对象,即看是求直角边长,还是斜边长或者两种均有可能;第三步:运用勾股定理进行计算.
探索新知
例3 〈实际应用题〉两棵树之间的距离为8 m,两棵树的高度分别是8 m,2 m,一只小鸟从一棵树的树顶飞到另一棵树的树顶,这只小鸟至少要飞多少米?
导引:先根据题意画出图形,然后添加辅助线,构造直角三角形,再利用勾股定理求解.
探索新知
解:根据题意画出示意图,如图所示,
两棵树的高度分别为AB=8 m,CD=2 m,
两棵树之间的距离BD=8 m,
过点C作CE⊥AB,垂足为E,连接AC.
则BE=CD=2 m,EC=BD=8 m,
AE=AB-BE=8-2=6(m).
在Rt△ACE中,由勾股定理,得AC2=AE2+EC2,
即AC2=62+82=100,所以AC=10 m.
答:这只小鸟至少要飞10 m.
典题精讲
如图,一个长为2.5 m的梯子,一端放在离墙脚1.5 m处,另一端靠墙,则梯子顶端距离墙脚( )
A.0.2 m B.0.4 m C.2 m D.4 m
C
典题精讲
2 如图,有两棵树,一棵高10 m,另一棵高4 m,两树相距8 m,一只小鸟从一棵树的树顶飞到另一棵树的树顶,小鸟至少飞行( )
A.8 m B.10 m C.12 m D.14 m
B
学以致用
小试牛刀
1.勾股定理的验证方法很多,主要是用________法说明,要注意两点:(1)通过割补、拼摆,用相同的直角三角形得到一个图形;
面积
(2)根据拼成的图形得到一个________关系式,通过恒等变形即可得到勾股定理.
例:图①反映的面积关系式为
___________________________;
图②反映的面积关系式为___________________________.
面积
小试牛刀
2.在Rt△ABC中,a,b是两直角边,c为斜边,如果已知a,b,那么c2=________;如果已知a,c,那么b2=________;如果已知b,c,那么a2=_______.当不能直接运用勾股定理求线段长度时,则设所求线段的长度为x,并选择一个合适的直角三角形,根据勾股定理,列出含________的方程.
a2+b2
c2-a2
c2-b2
x
A.S△EDA=S△CEB
B.S△EDA+S△CEB=S△CDE
C.S四边形CDAE=S四边形CDEB
D.S△EDA+S△CDE+S△CEB=S四边形ABCD
小试牛刀
3.历史上对勾股定理的一种验证方法采用了如图所示的图形,其中两个全等直角三角形的边AE,EB在一条直线上,其中用到的面积相等的关系式是( )
D
小试牛刀
4.九章算术》中的“折竹抵地”问题(如图):今有竹高一丈,末折抵地,去根六尺,问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )
A.x2-6=(10-x)2
B.x2-62=(10-x)2
C.x2+6=(10-x)2
D.x2+62=(10-x)2
D
小试牛刀
5.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙脚的距离为0.7 m,顶端距离地面2.4 m.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2 m,则小巷的宽度为( )
A.0.7 m B.1.5 m
C.2.2 m D.2.4 m
C
小试牛刀
6.如图,在正方形网格中,每个小正方形的边长均为1,△ABC在网格中,顶点均为格点.求点A到直线BC的距离.
S△ABC=4×5- ×2×5- ×2×2- ×3×4=7.
因为BC2=32+42=52,所以BC=5.
设点A到直线BC的距离为h,
因为S△ABC= BC h,
所以 ×5h=7,所以h= .
故点A到直线BC的距离是 .
小试牛刀
7.如图,AD是△ABC的中线,试说明AB2+AC2=2(AD2+CD2).
过点A作AE⊥BC于点E.
在Rt△ABE,Rt△ACE和Rt△ADE中,由勾股定理得
AB2=AE2+BE2,AC2=AE2+EC2,AE2=AD2-DE2,
因为AD是△ABC的中线,所以BD=CD.所以AB2+AC2=2AD2+2CD2,即AB2+AC2=2(AD2+CD2).
所以AB2+AC2=2AE2+BE2+EC2=2(AD2-DE2)+(BD-DE)2+(CD+DE)2=2AD2-2DE2+BD2-2BD DE+DE2+CD2+2CD DE+DE2
=2AD2+BD2+CD2-2BD DE+2CD DE.
小试牛刀
8.如图,在一棵树的10 m高的B处有两只猴子,其中一只猴子爬下树,走到离树20 m处的池塘A处,另一只猴子爬到树顶D后直接跃向池塘A处(假设它跃过的路线为直线).如果两只猴子所经过的路程相等,求这棵树的高.
【思路点拨】通过设未知数,根据两只猴子经过的路程相等表示出AD的长度,再利用勾股定理列方程求解.
小试牛刀
解:
设BD=x m,由题意知BC+AC=BD+AD,
所以AD=(30-x)m.
所以(10+x)2+202=(30-x)2. 解得x=5.
所以x+10=15,即这棵树的高为15 m.
课堂小结
课堂小结
用拼图验证勾股定理的方法:首先通过拼图找出面积之间的相等关系,再由面积之间的相等关系结合图形进行代数变形即可推导出勾股定理.
它一般都经过以下几个步骤:拼出图形→写出图形面积的表达式→找出相等关系→恒等变形→导出勾股定理.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
