北师大版(新)八上-1.3 勾股定理的应用【优质课件】
文档属性
| 名称 | 北师大版(新)八上-1.3 勾股定理的应用【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览







文档简介
(共36张PPT)
1.3 勾股定理的应用
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1、勾股定理的内容是什么?
2、勾股定理的逆定理是什么?
复
习
提
问
新课精讲
探索新知
1
知识点
勾股定理及直角三角形的判定在求最值中的应用
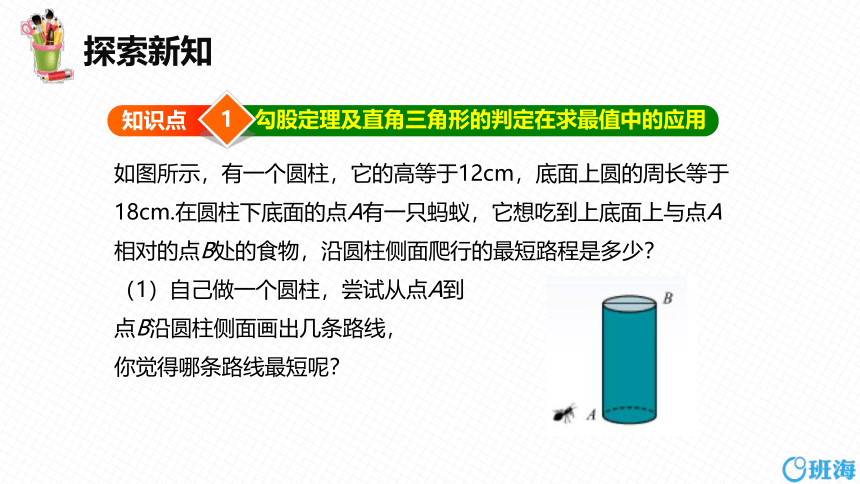
如图所示,有一个圆柱,它的高等于12cm,底面上圆的周长等于18cm.在圆柱下底面的点A有一只蚂蚁,它想吃到上底面上与点A相对的点B处的食物,沿圆柱侧面爬行的最短路程是多少?
(1)自己做一个圆柱,尝试从点A到
点B沿圆柱侧面画出几条路线,
你觉得哪条路线最短呢?
探索新知
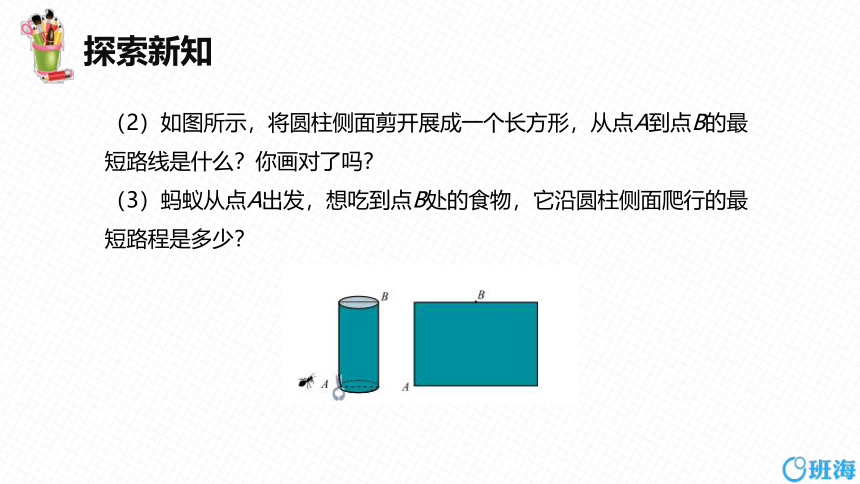
(2)如图所示,将圆柱侧面剪开展成一个长方形,从点A到点B的最短路线是什么?你画对了吗?
(3)蚂蚁从点A出发,想吃到点B处的食物,它沿圆柱侧面爬行的最短路程是多少?
探索新知
求圆柱侧面上两点间的最短路线长的方法:
先将圆柱的侧面展开,确定两点的位置,两点连接的线段即为最短路线,再在直角三角形中,利用勾股定理求其长度即可.
探索新知
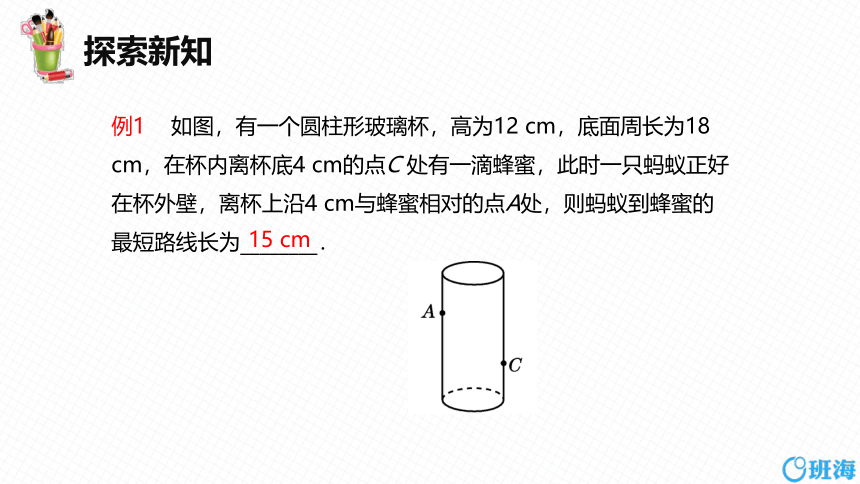
例1 如图,有一个圆柱形玻璃杯,高为12 cm,底面周长为18 cm,在杯内离杯底4 cm的点C 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4 cm与蜂蜜相对的点A处,则蚂蚁到蜂蜜的最短路线长为________.
15 cm
探索新知
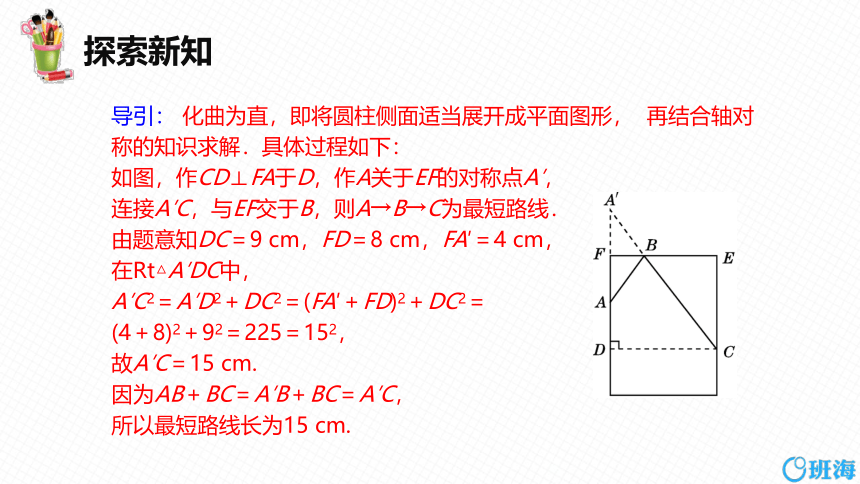
导引: 化曲为直,即将圆柱侧面适当展开成平面图形, 再结合轴对称的知识求解.具体过程如下:
如图,作CD⊥FA于D,作A关于EF的对称点A′,
连接A′C,与EF交于B,则A→B→C为最短路线.
由题意知DC=9 cm,FD=8 cm,FA′=4 cm,
在Rt△A′DC中,
A′C2=A′D2+DC2=(FA′+FD)2+DC2=
(4+8)2+92=225=152,
故A′C=15 cm.
因为AB+BC=A′B+BC=A′C,
所以最短路线长为15 cm.
探索新知
2
知识点
勾股定理及直角三角形的判定的实际应用
1.求长方体(或正方体)表面上两点间的最短路线长的方法:
先将长方体(或正方体)的表面展成平面图形,展开时一般要考虑各种可能的情况.在各种可能的情况中,分别确定两点的位置并连接成线段,再利用勾股定理分别求其长度,长度最短的路线为最短路线.
探索新知
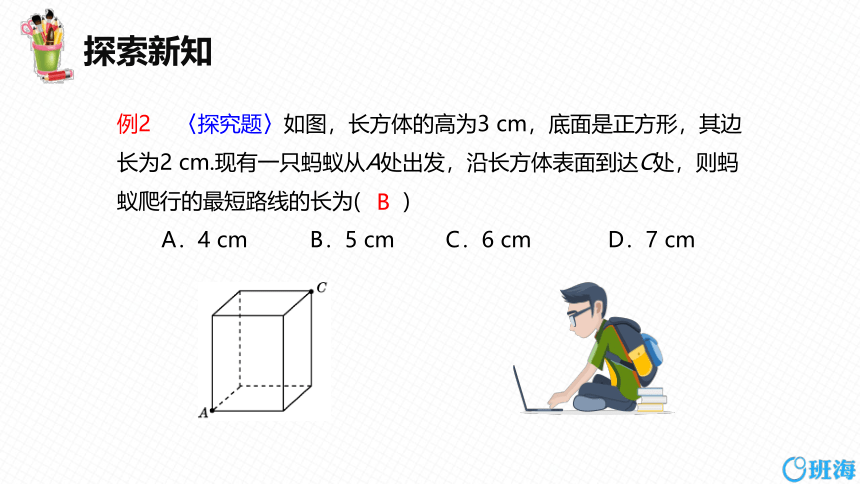
例2 〈探究题〉如图,长方体的高为3 cm,底面是正方形,其边长为2 cm.现有一只蚂蚁从A处出发,沿长方体表面到达C处,则蚂蚁爬行的最短路线的长为( )
A.4 cm B.5 cm C.6 cm D.7 cm
B
探索新知
导引: 考虑将长方体表面展开成平面图形的各种情况,分类讨论求解.如图,连接AC.在图①中,AC2=(2+2)2+32=25;在图②中,AC2=22+(3+2)2=29.因为29>25,所以蚂蚁爬行的最短路线的长为5 cm.
典题精讲
如图,正方体的边长为1,一只蚂蚁沿正方体的表面从一个顶点A爬行到另一个顶点B,则蚂蚁爬行的最短路程的平方是( )
A.2
B.3
C.4
D.5
D
探索新知
做一做
李叔叔想要检测雕塑(如图)底座正面的边AD和边BC是否分别
垂直于底边AB,但他随身只带了卷尺.
(1)你能替他想办法完成任务吗?
(2)李叔叔量得边AD长是30cm,
边AB长是40cm,点B,D之间的距
离是50cm,边AD垂直于边AB吗
(3)小明随身只有一个长度为20cm的刻度尺,他能有办法检验
边AD是否垂直于边AB吗?边BC与边AB呢?
探索新知
1. 在解一些求高度、宽度、长度、距离等的问题时,首先要结合题意画出符合要求的直角三角形,也就是把实际问题转化为数学问题,进而把要求的量看作直角三角形的一条边,然后利用勾股定理进行求解.
2. 在日常生活中,判断一个角是否为直角时,除了用三角板、量角器等测量角度的工具外,还可以通过测量长度,结合计算来判断.
探索新知
例3 如图是一个滑梯示意图,若将滑道AC水平放置,则刚好与AB一样长.已知滑梯的高度 CE=3m, CD=1m,试求滑道AC的长.
解:设滑道AC的长度为xm,则AB的长度为xm,
AE的长度为(x-1)m,
在Rt△ACE中,∠AEC=90°,
由勾股定理得AE 2+CE 2=AC 2,即(x-1)2+32=x2,
解得x=5.故滑道AC的长度为5m.
探索新知
例4 〈实际应用题〉假期中,小明和同学们到某海岛上去探宝旅游,按照探宝图,他们在点A登陆后先 往东走8 km到达C处,又往北走了2 km,遇到障碍后又往西走了3 km,再往北走了6 km后往东拐,仅走了1 km就找到了藏宝点B,如图,登陆点A到藏宝点B的距离是________.
10km
探索新知
导引:如图,过点B作BD⊥AC,垂足为D,连接AB,则看图可以得出AD,BD的长度,在直角三角形ABD中,AB为斜边,根据勾股定理计算出AB的长即可.
典题精讲
已知A,B,C三地位置如图所示,∠C=90°,A,C两地的距离是4 km,B,C两地的距离是3 km,则A,B两地的距离是________;若A地在C地的正东方向,则B地在C地的________方向.
5 km
正北
1
典题精讲
如图,甲货船以16 n mile/h的速度从港口A出发向东北方向航行,乙货船以12 n mile/h的速度同时从港口A出发向东南方向航行,离开港口3 h时两船相距( )
A.35 n mile
B.50 n mile
C.60 n mile
D.40 n mile
C
2
学以致用
小试牛刀
1.最短路线的求法:因为在平面内,两点之间________最短,所以在求立体图形中两点间的最短距离时,首先把立体图形转化为平面图形,然后利用__________来求,或利用“两点一线”型,用对称点法找出点,然后用__________求解.
线段
勾股定理
勾股定理
2.在求一些高度、长度、距离、宽度等量时,首先要结合题意画出符合要求的________________,也就是把实际问题转化为____________,进而把要求的量看成直角三角形的一条边长,然后利用勾股定理进行求解.
直角三角形
数学问题
小试牛刀
3.如图,已知∠B=∠C=∠D=∠E=90°,且AB=CD=3,BC=4,DE=EF=2,则AF的长是________.
10
4.如图,在一个高为3 m,长为5 m的楼梯表面铺地毯,则地毯长度为________.
7m
小试牛刀
5.如图,学校有一块长方形花圃,有极少数人从A走到B,为了避免拐角C走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了________步路(假设2步为1 m),却踩伤了花草.
4
小试牛刀
6.如图,圆柱的底面直径为 ,BC=12,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离为( )
A.10
B.12
C.20
D.14
A
小试牛刀
7.如图,牧童在A处放牛,牧童家在B处,A,B处距河岸的距离AC,BD的长分别为500 m和700 m,且C,D两地距离为500 m,天黑前牧童从A点将牛牵到河边饮水,再赶回家,那么牧童最少要走( )
A.1 000 m B.1 200 m
C.1 300 m D.1 700 m
C
小试牛刀
8.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8 m处,发现此时绳子末端距离地面2 m,则旗杆的高度(滑轮上方的部分忽略不计)为( )
A.12 m B.13 m
C.16 m D.17 m
D
小试牛刀
9.如图,长方体的高为3 cm,底面是正方形,边长为2 cm,现有绳子从D出发,沿长方体表面到达B′点,问:绳子最短是多少厘米?
如图①,连接DB′,在Rt△DD′B′中,由勾股定理得DB′2=32+42=25.
如图②,连接DB′,在Rt△DC′B′中,由勾股定理得DB′2=22+52=29.
因为29>25,所以第一种情况绳子最短.
故绳子最短为5 cm.
小试牛刀
10.为筹备迎接新生晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕红色油纸,如图所示.已知圆筒的高为108 cm,其横截面周长为36cm,如果在侧面上均匀缠绕油纸4圈,应裁剪多长的油纸?
如图,在Rt△ABC中,
AC=36 cm,BC=108÷4=27(cm).
由勾股定理得
AB2=AC2+BC2=362+272=2 025=452,
所以AB=45 cm.整个油纸的长为45×4=180(cm).
故应裁剪180 cm长的油纸.
小试牛刀
11.如图是一个三级台阶,它的每一级的长、宽、高分别为20 dm,3 dm,2 dm,A和B是这个台阶两个相对的点,B点有一只蚂蚁,想到A点去吃可口的食物,则蚂蚁沿着台阶面爬到A点的最短路程是多少?
将台阶面展开成如图所示的平面图形,
则BD=15 dm,AD=20 dm,连接AB.
在Rt△ADB中,
AB2=AD2+DB2=202+152=625,
所以AB=25 dm.
所以最短路程是25 dm.
小试牛刀
12.如图,一个正方体木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.
(1)请你在正方体木柜的表面展开图中画出蚂蚁能够最快到达目的地的可能路径;
(1)蚂蚁能够最快到达目的地的可能
路径为如图所示的AC′1和AC1.
解:
小试牛刀
(2)如图,AC′12=42+(4+4)2=80.
AC12=(4+4)2+42=80.
所以蚂蚁爬过的最短路径的长的平方是80.
(2)当正方体木柜的棱长为4时,求蚂蚁爬过的最短路径的长的平方.
课堂小结
课堂小结
1.解决实际问题的方法是建立数学模型求解.
2.在寻求最短路径时,往往把空间问题平面化,利用勾股定理及其逆定理解决实际问题.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
1.3 勾股定理的应用
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1、勾股定理的内容是什么?
2、勾股定理的逆定理是什么?
复
习
提
问
新课精讲
探索新知
1
知识点
勾股定理及直角三角形的判定在求最值中的应用
如图所示,有一个圆柱,它的高等于12cm,底面上圆的周长等于18cm.在圆柱下底面的点A有一只蚂蚁,它想吃到上底面上与点A相对的点B处的食物,沿圆柱侧面爬行的最短路程是多少?
(1)自己做一个圆柱,尝试从点A到
点B沿圆柱侧面画出几条路线,
你觉得哪条路线最短呢?
探索新知
(2)如图所示,将圆柱侧面剪开展成一个长方形,从点A到点B的最短路线是什么?你画对了吗?
(3)蚂蚁从点A出发,想吃到点B处的食物,它沿圆柱侧面爬行的最短路程是多少?
探索新知
求圆柱侧面上两点间的最短路线长的方法:
先将圆柱的侧面展开,确定两点的位置,两点连接的线段即为最短路线,再在直角三角形中,利用勾股定理求其长度即可.
探索新知
例1 如图,有一个圆柱形玻璃杯,高为12 cm,底面周长为18 cm,在杯内离杯底4 cm的点C 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4 cm与蜂蜜相对的点A处,则蚂蚁到蜂蜜的最短路线长为________.
15 cm
探索新知
导引: 化曲为直,即将圆柱侧面适当展开成平面图形, 再结合轴对称的知识求解.具体过程如下:
如图,作CD⊥FA于D,作A关于EF的对称点A′,
连接A′C,与EF交于B,则A→B→C为最短路线.
由题意知DC=9 cm,FD=8 cm,FA′=4 cm,
在Rt△A′DC中,
A′C2=A′D2+DC2=(FA′+FD)2+DC2=
(4+8)2+92=225=152,
故A′C=15 cm.
因为AB+BC=A′B+BC=A′C,
所以最短路线长为15 cm.
探索新知
2
知识点
勾股定理及直角三角形的判定的实际应用
1.求长方体(或正方体)表面上两点间的最短路线长的方法:
先将长方体(或正方体)的表面展成平面图形,展开时一般要考虑各种可能的情况.在各种可能的情况中,分别确定两点的位置并连接成线段,再利用勾股定理分别求其长度,长度最短的路线为最短路线.
探索新知
例2 〈探究题〉如图,长方体的高为3 cm,底面是正方形,其边长为2 cm.现有一只蚂蚁从A处出发,沿长方体表面到达C处,则蚂蚁爬行的最短路线的长为( )
A.4 cm B.5 cm C.6 cm D.7 cm
B
探索新知
导引: 考虑将长方体表面展开成平面图形的各种情况,分类讨论求解.如图,连接AC.在图①中,AC2=(2+2)2+32=25;在图②中,AC2=22+(3+2)2=29.因为29>25,所以蚂蚁爬行的最短路线的长为5 cm.
典题精讲
如图,正方体的边长为1,一只蚂蚁沿正方体的表面从一个顶点A爬行到另一个顶点B,则蚂蚁爬行的最短路程的平方是( )
A.2
B.3
C.4
D.5
D
探索新知
做一做
李叔叔想要检测雕塑(如图)底座正面的边AD和边BC是否分别
垂直于底边AB,但他随身只带了卷尺.
(1)你能替他想办法完成任务吗?
(2)李叔叔量得边AD长是30cm,
边AB长是40cm,点B,D之间的距
离是50cm,边AD垂直于边AB吗
(3)小明随身只有一个长度为20cm的刻度尺,他能有办法检验
边AD是否垂直于边AB吗?边BC与边AB呢?
探索新知
1. 在解一些求高度、宽度、长度、距离等的问题时,首先要结合题意画出符合要求的直角三角形,也就是把实际问题转化为数学问题,进而把要求的量看作直角三角形的一条边,然后利用勾股定理进行求解.
2. 在日常生活中,判断一个角是否为直角时,除了用三角板、量角器等测量角度的工具外,还可以通过测量长度,结合计算来判断.
探索新知
例3 如图是一个滑梯示意图,若将滑道AC水平放置,则刚好与AB一样长.已知滑梯的高度 CE=3m, CD=1m,试求滑道AC的长.
解:设滑道AC的长度为xm,则AB的长度为xm,
AE的长度为(x-1)m,
在Rt△ACE中,∠AEC=90°,
由勾股定理得AE 2+CE 2=AC 2,即(x-1)2+32=x2,
解得x=5.故滑道AC的长度为5m.
探索新知
例4 〈实际应用题〉假期中,小明和同学们到某海岛上去探宝旅游,按照探宝图,他们在点A登陆后先 往东走8 km到达C处,又往北走了2 km,遇到障碍后又往西走了3 km,再往北走了6 km后往东拐,仅走了1 km就找到了藏宝点B,如图,登陆点A到藏宝点B的距离是________.
10km
探索新知
导引:如图,过点B作BD⊥AC,垂足为D,连接AB,则看图可以得出AD,BD的长度,在直角三角形ABD中,AB为斜边,根据勾股定理计算出AB的长即可.
典题精讲
已知A,B,C三地位置如图所示,∠C=90°,A,C两地的距离是4 km,B,C两地的距离是3 km,则A,B两地的距离是________;若A地在C地的正东方向,则B地在C地的________方向.
5 km
正北
1
典题精讲
如图,甲货船以16 n mile/h的速度从港口A出发向东北方向航行,乙货船以12 n mile/h的速度同时从港口A出发向东南方向航行,离开港口3 h时两船相距( )
A.35 n mile
B.50 n mile
C.60 n mile
D.40 n mile
C
2
学以致用
小试牛刀
1.最短路线的求法:因为在平面内,两点之间________最短,所以在求立体图形中两点间的最短距离时,首先把立体图形转化为平面图形,然后利用__________来求,或利用“两点一线”型,用对称点法找出点,然后用__________求解.
线段
勾股定理
勾股定理
2.在求一些高度、长度、距离、宽度等量时,首先要结合题意画出符合要求的________________,也就是把实际问题转化为____________,进而把要求的量看成直角三角形的一条边长,然后利用勾股定理进行求解.
直角三角形
数学问题
小试牛刀
3.如图,已知∠B=∠C=∠D=∠E=90°,且AB=CD=3,BC=4,DE=EF=2,则AF的长是________.
10
4.如图,在一个高为3 m,长为5 m的楼梯表面铺地毯,则地毯长度为________.
7m
小试牛刀
5.如图,学校有一块长方形花圃,有极少数人从A走到B,为了避免拐角C走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了________步路(假设2步为1 m),却踩伤了花草.
4
小试牛刀
6.如图,圆柱的底面直径为 ,BC=12,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离为( )
A.10
B.12
C.20
D.14
A
小试牛刀
7.如图,牧童在A处放牛,牧童家在B处,A,B处距河岸的距离AC,BD的长分别为500 m和700 m,且C,D两地距离为500 m,天黑前牧童从A点将牛牵到河边饮水,再赶回家,那么牧童最少要走( )
A.1 000 m B.1 200 m
C.1 300 m D.1 700 m
C
小试牛刀
8.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8 m处,发现此时绳子末端距离地面2 m,则旗杆的高度(滑轮上方的部分忽略不计)为( )
A.12 m B.13 m
C.16 m D.17 m
D
小试牛刀
9.如图,长方体的高为3 cm,底面是正方形,边长为2 cm,现有绳子从D出发,沿长方体表面到达B′点,问:绳子最短是多少厘米?
如图①,连接DB′,在Rt△DD′B′中,由勾股定理得DB′2=32+42=25.
如图②,连接DB′,在Rt△DC′B′中,由勾股定理得DB′2=22+52=29.
因为29>25,所以第一种情况绳子最短.
故绳子最短为5 cm.
小试牛刀
10.为筹备迎接新生晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕红色油纸,如图所示.已知圆筒的高为108 cm,其横截面周长为36cm,如果在侧面上均匀缠绕油纸4圈,应裁剪多长的油纸?
如图,在Rt△ABC中,
AC=36 cm,BC=108÷4=27(cm).
由勾股定理得
AB2=AC2+BC2=362+272=2 025=452,
所以AB=45 cm.整个油纸的长为45×4=180(cm).
故应裁剪180 cm长的油纸.
小试牛刀
11.如图是一个三级台阶,它的每一级的长、宽、高分别为20 dm,3 dm,2 dm,A和B是这个台阶两个相对的点,B点有一只蚂蚁,想到A点去吃可口的食物,则蚂蚁沿着台阶面爬到A点的最短路程是多少?
将台阶面展开成如图所示的平面图形,
则BD=15 dm,AD=20 dm,连接AB.
在Rt△ADB中,
AB2=AD2+DB2=202+152=625,
所以AB=25 dm.
所以最短路程是25 dm.
小试牛刀
12.如图,一个正方体木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.
(1)请你在正方体木柜的表面展开图中画出蚂蚁能够最快到达目的地的可能路径;
(1)蚂蚁能够最快到达目的地的可能
路径为如图所示的AC′1和AC1.
解:
小试牛刀
(2)如图,AC′12=42+(4+4)2=80.
AC12=(4+4)2+42=80.
所以蚂蚁爬过的最短路径的长的平方是80.
(2)当正方体木柜的棱长为4时,求蚂蚁爬过的最短路径的长的平方.
课堂小结
课堂小结
1.解决实际问题的方法是建立数学模型求解.
2.在寻求最短路径时,往往把空间问题平面化,利用勾股定理及其逆定理解决实际问题.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
