北师大版数学九年级上册同步提优训练:第2章 一元二次方程 单元综合提升卷(word版 含解析)
文档属性
| 名称 | 北师大版数学九年级上册同步提优训练:第2章 一元二次方程 单元综合提升卷(word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 132.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-11 20:51:20 | ||
图片预览




文档简介
第二章综合提升卷
第Ⅰ卷 (选择题 共30分)
一、选择题(每小题3分,共30分)
1.下列方程中是关于x的一元二次方程的是 ( )
A.x2+=0 B.ax2+bx+c=0
C.(x-1)(x+2)=1 D.3x2-2xy-5y2=0
2.用配方法解一元二次方程=0时,下列变形正确的是( )
A.(x+3)2=1 B.(x-3)2=1 C.(x+3)2=19 D.(x-3)2=19
3.已知关于x的方程(4-a)=0是一元二次方程,则它的一次项系数是 ( )
A.-1 B.1 C.4 D.4或-1
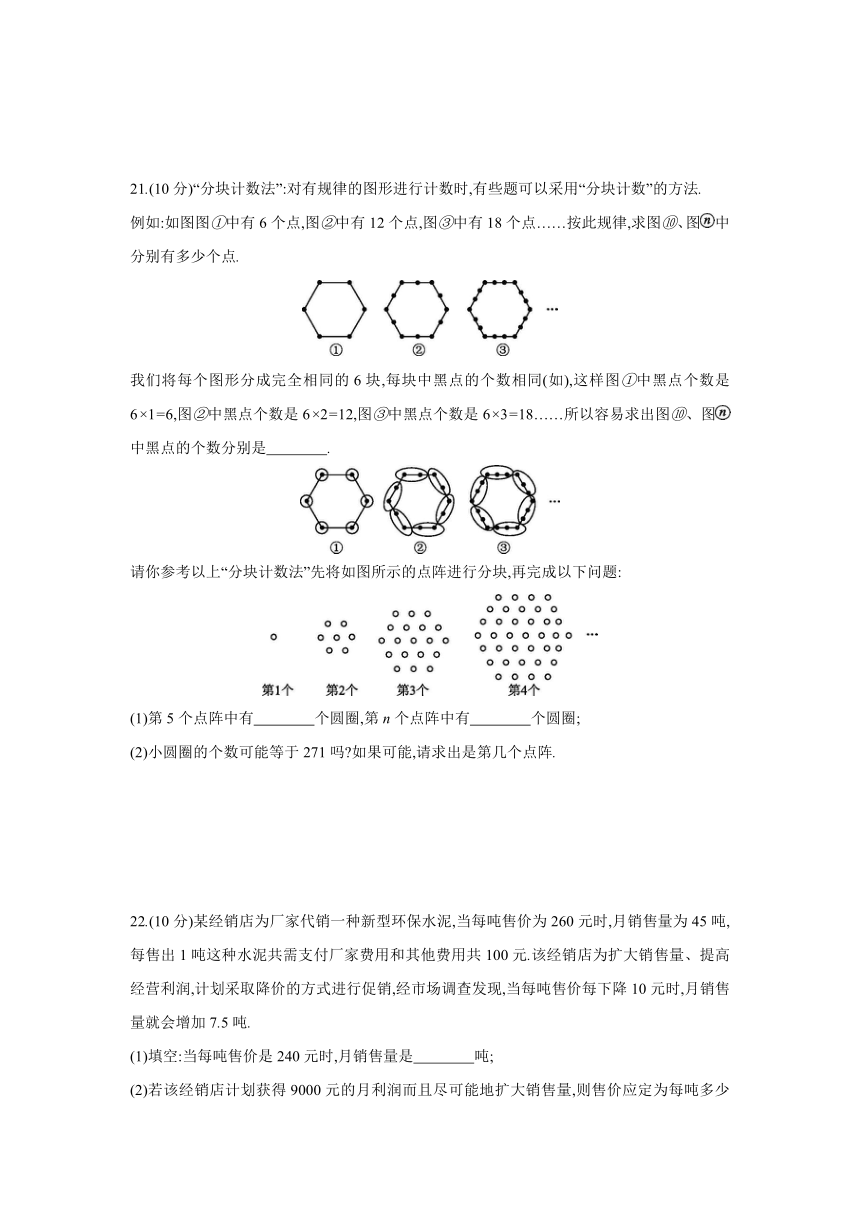
4.若2-是方程x2-4x+c=0的一个根,则c的值是 ( )
A.1 B.3- C.1+ D.2+
5.已知关于x的方程mx2-2x+1=0有两个不相等的实数根,则m的取值范围是 ( )
A.m<1 B.m>1 C.m<1且m≠0 D.m≤1
6.若关于x的方程x2+2x-3=0与=有一个相同的根,则a的值为 ( )
A.1 B.1或-3 C.-1 D.-1或3
7.某种植基地2021年蔬菜产量为80吨,预计2023年蔬菜产量达到100吨,求蔬菜产量的年平均增长率.设蔬菜产量的年平均增长率为x,则可列方程为 ( )
A.80(1+x)2=100 B.80(1-x)2=100
C.80(1+2x)=100 D.80(1+x2)=100
8.已知3是关于x的方程x2-(m+1)x+2m=0的一个实数根,并且这个方程的两个实数根恰好是等腰三角形ABC的两条边的长,则△ABC的周长为 ( )
A.7 B.10 C.11 D.10或11
9.若a满足不等式组则关于x的方程(a-2)x2-(2a-1)x+a+=0的根的情况是 ( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.以上三种情况都有可能
10.欧几里得的《原本》记载,形如x2+ax=b2的方程的图解法是:如图画Rt△ABC,使∠ACB=90°,BC=,AC=b,再在斜边AB上截取BD=,则该方程的一个正根是 ( )
A.AC的长 B.AD的长 C.BC的长 D.CD的长
请将选择题答案填入下表:
题号 1 2 3 4 5 6 7 8 9 10 总分
答案
第Ⅱ卷 (非选择题 共90分)
二、填空题(每小题3分,共18分)
11.在估算一元二次方程x2+12x-15=0的根时,小彬列表如下:
x 1 1.1 1.2 1.3
x2+12x-15 -2 -0.59 0.84 2.29
由此可估算方程x2+12x-15=0的一个根x的范围是 .
12.如果关于x的方程ax2+4x-2=0(a≠0)有实数根,那么负整数a= (写一个即可).
13.设x1,x2是关于x的方程x2-3x+k=0的两个根,且x1=2x2,则k= .
14.某种花卉每盆的赢利与每盆的株数有一定的关系.每盆植3株时,平均每株赢利4元;若每盆增加1株,则平均每株赢利减少0.5元.要使每盆的赢利达到15元,则每盆应多植多少株 设每盆多植x株,则可以列出的方程是 .
15.若等腰三角形的一边长是4,另两边的长是关于x的方程x2-6x+n=0的两个根,则n的值为 .
16.对于一元二次方程ax2+bx+c=0(a≠0),有下列说法:
①若a+c=0,则方程ax2+bx+c=0必有实数根;
②若b2+4ac<0,则方程ax2+bx+c=0一定有实数根;
③若a-b+c=0,则方程ax2+bx+c=0一定有两个不相等的实数根;
④若方程ax2+bx+c=0有两个实数根,则方程cx2+bx+a=0一定有两个实数根.
其中正确的有 (填序号).
三、解答题(共72分)
17.(6分)用适当的方法解下列方程:
(1)(x+1)(x-2)=x-2;
(2)(2x+1)2=x2+2.
18.(6分)已知m是方程=0的一个根,且m>0,求代数式的值.
19.(8分)已知关于x的一元二次方程x(x-2)=x-2①与一元一次方程2x+1=2a-x②.
(1)若方程①的一个根是方程②的根,求a的值;
(2)若方程②的根不小于方程①两根中的较小根且不大于方程①两根中的较大根,求a的取值范围.
20.(8分)已知关于x的一元二次方程(x-1)(x-4)=a2,其中a为常数.
(1)求证:此方程有两个不相等的实数根;
(2)当|a-2|=0时,求此方程的根.
21.(10分)“分块计数法”:对有规律的图形进行计数时,有些题可以采用“分块计数”的方法.
例如:如图图①中有6个点,图②中有12个点,图③中有18个点……按此规律,求图⑩、图中分别有多少个点.
我们将每个图形分成完全相同的6块,每块中黑点的个数相同(如),这样图①中黑点个数是6×1=6,图②中黑点个数是6×2=12,图③中黑点个数是6×3=18……所以容易求出图⑩、图中黑点的个数分别是 .
请你参考以上“分块计数法”先将如图所示的点阵进行分块,再完成以下问题:
(1)第5个点阵中有 个圆圈,第n个点阵中有 个圆圈;
(2)小圆圈的个数可能等于271吗 如果可能,请求出是第几个点阵.
22.(10分)某经销店为厂家代销一种新型环保水泥,当每吨售价为260元时,月销售量为45吨,每售出1吨这种水泥共需支付厂家费用和其他费用共100元.该经销店为扩大销售量、提高经营利润,计划采取降价的方式进行促销,经市场调查发现,当每吨售价每下降10元时,月销售量就会增加7.5吨.
(1)填空:当每吨售价是240元时,月销售量是 吨;
(2)若该经销店计划获得9000元的月利润而且尽可能地扩大销售量,则售价应定为每吨多少元
23.(12分)某住宅小区在住宅建设时留下一块1798平方米的矩形空地,准备建一个矩形的露天游泳池,设计示意图如图所示,游泳池的长是宽的2倍,在游泳池的前侧留一块5米宽的空地,其他三侧各保留2米宽的道路及1米宽的绿化带.
(1)请你计算出游泳池的长和宽;
(2)已知贴1平方米瓷砖需费用50元,若游泳池深3米,现要把池底和池壁(共5个面)都贴上瓷砖,共需要费用多少元
24.(12分)如图在矩形ABCD中,AB=6 cm,AD=2 cm,点P以2 cm/s的速度从顶点A出发沿折线A-B-C向点C运动,同时点Q以1 cm/s的速度从顶点C出发向点D运动,当其中一个动点到达终点停止运动时,另一点也停止运动.
(1)两动点运动几秒后,四边形PBCQ的面积是矩形ABCD面积的
(2)是否存在某一时刻使得点P与点Q之间的距离为 cm 若存在,请求出运动所需的时间;若不存在,请说明理由.
答案
第二章综合提升卷
1.C 2.D
3.B 由题意,得=2且4-a≠0,解得a=-1,故它的一次项系数是1.故选B.
4.A ∵2-是方程x2-4x+c=0的一个根,∴(2-)2-4(2-)+c=0.∴c=1.故选A.
5.C ∵关于x的方程mx2-2x+1=0有两个不相等的实数根,∴m≠0,Δ=(-2)2-4×m×1>0,
解得m<1且m≠0.
故选C.
6.C 解方程x2+2x-3=0,得x1=1,
x2=-3.
∵x=-3是方程=的增根,∴x=1是方程=的根.∴=.解得a=-1.故选C.
7.A 由题意知,蔬菜产量的年平均增长率为x,根据2021年蔬菜产量为80吨,则2022年蔬菜产量为80(1+x)吨,2023年蔬菜产量为80(1+x)(1+x)吨.预计2023年蔬菜产量达到100吨,则80(1+x)(1+x)=100,即80(1+x)2=100.
8.D 把x=3代入方程,得9-3(m+1)+2m=0,解得m=6,则原方程为x2-7x+12=0,解得x1=3,x2=4.因为这个方程的两个实数根恰好是等腰三角形ABC的两条边长,①若△ABC的腰长为4,底边长为3,则△ABC的周长为4+4+3=11;②若△ABC的腰长为3,底边长为4,则△ABC的周长为3+3+4=10.综上所述,△ABC的周长为10或11.故选D.
9.C 解不等式组得a<-3.
∵Δ=(2a-1)2-4(a-2)=2a+5,a<-3,
∴Δ=2a+5<0.
∴关于x的方程(a-2)x2-(2a-1)x+a+=0没有实数根.
10.B 利用配方法解方程x2+ax=b2,得到x+2=b2+,则方程的一个正根是x=-.根据勾股定理知道,AB=,而BD=,根据图形知道AD=AB-BD,即AD的长是方程的一个正根.故正确答案为B.
11.1.11(答案不唯一,写其中一个即可)
关于x的方程ax2+4x-2=0(a≠0)有实数根,那么Δ=42-4·a·(-2)≥0,解得a≥-2.由于a是负整数,因此a可.
13.2 根据题意,知x1+x2=3x2=3,解得x2=1.
将其代入关于x的方程x2-3x+k=0,得1-3×1+k=0,
解得k=2.
故答案是2.
14.(3+x)(4-0.5x)=15
15.8或9 当4为腰长时,将x=4代入x2-6x+n=0,得42-6×4+n=0,
解得n=8,
当n=8时,原方程为x2-6x+8=0,
解得x1=2,x2=4.
∵2+4>4,∴n=8符合题意;
当4为底边长时,关于x的方程x2-6x+n=0有两个相等的实数根,
∴Δ=(-6)2-4×1×n=0,解得n=9.
当n=9时,原方程为x2-6x+9=0,
解得x1=x2=3.
∵3+3=6>4,∴n=9符合题意.
故答案为8或9.
16.①②
17.解:(1)(x+1)(x-)=0.
(x-2)(x+1-1)=0.
x-2=0或x+1-1=0.
所以x1=2,x2=0.
(2)原方程整理得3x2+4x-1=0.
Δ=42-4×3×(-1)=28,
x==,
所以x1=,x2=.
18.解:=0,x2-2x=2,x2-2x+1=3,
(x-1)2=3,x=±+1.
∵m>0,∴m=+1.
∴=m-1=.
19.解:(1)解方程①,得x1=1,x2=2;
解方程②,得x=.
当=1时,a=2;当=2时,a=.
综上所述,a的值是2或.
(2)由题意可知1≤≤2,解得2≤a≤.
20.解:(1)证明:原方程可整理为x2-5x+4-a2=0.
∵Δ=25-4(4-a2)=4a2+9>0,
∴此方程有两个不相等的实数根.
(2)∵|a-2|=0,∴a=2.
原方程可整理为x2-5x=0.
解得x1=0,x2=5.
21.解:60,6n
画图略
(1)61 (3n2-3n+1)
(2)可能.
令3n2-3n+1=271,
则=0,
(n-10)(n+9)=0.
解得n1=10,n2=-9(舍去).
∴小圆圈的个数可能等于271,它是第10个点阵.
22.解:(1)60
(2)解法一:设每吨售价下降10x元.
由题意,可列方程(260-100-10x)(45+7.5x)=9000.
化简,得x2-10x+24=0.解得x1=4,x2=6.
所以当售价定为每吨200元或220元时,该经销店的月利润均为9000元.
当售价定为每吨200元时,月销售量更大,所以售价应定为每吨200元.
解法二:设售价定为每吨x元.
由题意,可列方程(x-100)45+×7.5=9000.
化简,得x2-420x+44000=0.
解得x1=200,x2=220.
因为要尽可能地扩大销售量,所以售价应定为每吨200元.
23.解:(1)设游泳池的宽为x米,则长为2x米.
根据题意,得
(2x+2+5+1)·(x+2+2+1+1)=1798.
整理,得x2+10x-875=0.
解得x1=-35(不合题意,舍去),x2=25.
∴2x=2×25=50.
故游泳池的长为50米,宽为25米.
(2)[(25×3+50×3)×2+25×50]×50=(450+1250)×50=1700×50=85000(元).
故共需要费用85000元.
24. (1)要使四边形PBCQ的面积是矩形ABCD面积的,此时点P应在AB上,才能构成四边形.根据“路程=速度×时间”,设两动点运动x s,分别用x表示BP,CQ的长,再根据梯形的面积公式列方程求解;
(2)根据勾股定理列方程即可,注意分情况考虑.
解:(1)设两动点运动x s后,四边形PBCQ的面积是矩形ABCD面积的,此时点P应在AB上.
根据题意,得BP=(6-2x)cm,CQ=x cm,矩形ABCD的面积是12 cm2,则有(x+6-2x)×2=12×,
解得x=.
即两动点运动 s后,四边形PBCQ的面积是矩形ABCD面积的.
(2)存在.设两动点经过t s时点P与点Q之间的距离为 cm.
①当0整理,得9t2-36t+35=0,解得t=或t=;
②当3整理,得5t2-32t+59=0,此时Δ=322-4×5×59=-156<0,此方程无解.
综上所述,当运动 s或 s时,点P与点Q之间的距离为 cm.
第Ⅰ卷 (选择题 共30分)
一、选择题(每小题3分,共30分)
1.下列方程中是关于x的一元二次方程的是 ( )
A.x2+=0 B.ax2+bx+c=0
C.(x-1)(x+2)=1 D.3x2-2xy-5y2=0
2.用配方法解一元二次方程=0时,下列变形正确的是( )
A.(x+3)2=1 B.(x-3)2=1 C.(x+3)2=19 D.(x-3)2=19
3.已知关于x的方程(4-a)=0是一元二次方程,则它的一次项系数是 ( )
A.-1 B.1 C.4 D.4或-1
4.若2-是方程x2-4x+c=0的一个根,则c的值是 ( )
A.1 B.3- C.1+ D.2+
5.已知关于x的方程mx2-2x+1=0有两个不相等的实数根,则m的取值范围是 ( )
A.m<1 B.m>1 C.m<1且m≠0 D.m≤1
6.若关于x的方程x2+2x-3=0与=有一个相同的根,则a的值为 ( )
A.1 B.1或-3 C.-1 D.-1或3
7.某种植基地2021年蔬菜产量为80吨,预计2023年蔬菜产量达到100吨,求蔬菜产量的年平均增长率.设蔬菜产量的年平均增长率为x,则可列方程为 ( )
A.80(1+x)2=100 B.80(1-x)2=100
C.80(1+2x)=100 D.80(1+x2)=100
8.已知3是关于x的方程x2-(m+1)x+2m=0的一个实数根,并且这个方程的两个实数根恰好是等腰三角形ABC的两条边的长,则△ABC的周长为 ( )
A.7 B.10 C.11 D.10或11
9.若a满足不等式组则关于x的方程(a-2)x2-(2a-1)x+a+=0的根的情况是 ( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.以上三种情况都有可能
10.欧几里得的《原本》记载,形如x2+ax=b2的方程的图解法是:如图画Rt△ABC,使∠ACB=90°,BC=,AC=b,再在斜边AB上截取BD=,则该方程的一个正根是 ( )
A.AC的长 B.AD的长 C.BC的长 D.CD的长
请将选择题答案填入下表:
题号 1 2 3 4 5 6 7 8 9 10 总分
答案
第Ⅱ卷 (非选择题 共90分)
二、填空题(每小题3分,共18分)
11.在估算一元二次方程x2+12x-15=0的根时,小彬列表如下:
x 1 1.1 1.2 1.3
x2+12x-15 -2 -0.59 0.84 2.29
由此可估算方程x2+12x-15=0的一个根x的范围是 .
12.如果关于x的方程ax2+4x-2=0(a≠0)有实数根,那么负整数a= (写一个即可).
13.设x1,x2是关于x的方程x2-3x+k=0的两个根,且x1=2x2,则k= .
14.某种花卉每盆的赢利与每盆的株数有一定的关系.每盆植3株时,平均每株赢利4元;若每盆增加1株,则平均每株赢利减少0.5元.要使每盆的赢利达到15元,则每盆应多植多少株 设每盆多植x株,则可以列出的方程是 .
15.若等腰三角形的一边长是4,另两边的长是关于x的方程x2-6x+n=0的两个根,则n的值为 .
16.对于一元二次方程ax2+bx+c=0(a≠0),有下列说法:
①若a+c=0,则方程ax2+bx+c=0必有实数根;
②若b2+4ac<0,则方程ax2+bx+c=0一定有实数根;
③若a-b+c=0,则方程ax2+bx+c=0一定有两个不相等的实数根;
④若方程ax2+bx+c=0有两个实数根,则方程cx2+bx+a=0一定有两个实数根.
其中正确的有 (填序号).
三、解答题(共72分)
17.(6分)用适当的方法解下列方程:
(1)(x+1)(x-2)=x-2;
(2)(2x+1)2=x2+2.
18.(6分)已知m是方程=0的一个根,且m>0,求代数式的值.
19.(8分)已知关于x的一元二次方程x(x-2)=x-2①与一元一次方程2x+1=2a-x②.
(1)若方程①的一个根是方程②的根,求a的值;
(2)若方程②的根不小于方程①两根中的较小根且不大于方程①两根中的较大根,求a的取值范围.
20.(8分)已知关于x的一元二次方程(x-1)(x-4)=a2,其中a为常数.
(1)求证:此方程有两个不相等的实数根;
(2)当|a-2|=0时,求此方程的根.
21.(10分)“分块计数法”:对有规律的图形进行计数时,有些题可以采用“分块计数”的方法.
例如:如图图①中有6个点,图②中有12个点,图③中有18个点……按此规律,求图⑩、图中分别有多少个点.
我们将每个图形分成完全相同的6块,每块中黑点的个数相同(如),这样图①中黑点个数是6×1=6,图②中黑点个数是6×2=12,图③中黑点个数是6×3=18……所以容易求出图⑩、图中黑点的个数分别是 .
请你参考以上“分块计数法”先将如图所示的点阵进行分块,再完成以下问题:
(1)第5个点阵中有 个圆圈,第n个点阵中有 个圆圈;
(2)小圆圈的个数可能等于271吗 如果可能,请求出是第几个点阵.
22.(10分)某经销店为厂家代销一种新型环保水泥,当每吨售价为260元时,月销售量为45吨,每售出1吨这种水泥共需支付厂家费用和其他费用共100元.该经销店为扩大销售量、提高经营利润,计划采取降价的方式进行促销,经市场调查发现,当每吨售价每下降10元时,月销售量就会增加7.5吨.
(1)填空:当每吨售价是240元时,月销售量是 吨;
(2)若该经销店计划获得9000元的月利润而且尽可能地扩大销售量,则售价应定为每吨多少元
23.(12分)某住宅小区在住宅建设时留下一块1798平方米的矩形空地,准备建一个矩形的露天游泳池,设计示意图如图所示,游泳池的长是宽的2倍,在游泳池的前侧留一块5米宽的空地,其他三侧各保留2米宽的道路及1米宽的绿化带.
(1)请你计算出游泳池的长和宽;
(2)已知贴1平方米瓷砖需费用50元,若游泳池深3米,现要把池底和池壁(共5个面)都贴上瓷砖,共需要费用多少元
24.(12分)如图在矩形ABCD中,AB=6 cm,AD=2 cm,点P以2 cm/s的速度从顶点A出发沿折线A-B-C向点C运动,同时点Q以1 cm/s的速度从顶点C出发向点D运动,当其中一个动点到达终点停止运动时,另一点也停止运动.
(1)两动点运动几秒后,四边形PBCQ的面积是矩形ABCD面积的
(2)是否存在某一时刻使得点P与点Q之间的距离为 cm 若存在,请求出运动所需的时间;若不存在,请说明理由.
答案
第二章综合提升卷
1.C 2.D
3.B 由题意,得=2且4-a≠0,解得a=-1,故它的一次项系数是1.故选B.
4.A ∵2-是方程x2-4x+c=0的一个根,∴(2-)2-4(2-)+c=0.∴c=1.故选A.
5.C ∵关于x的方程mx2-2x+1=0有两个不相等的实数根,∴m≠0,Δ=(-2)2-4×m×1>0,
解得m<1且m≠0.
故选C.
6.C 解方程x2+2x-3=0,得x1=1,
x2=-3.
∵x=-3是方程=的增根,∴x=1是方程=的根.∴=.解得a=-1.故选C.
7.A 由题意知,蔬菜产量的年平均增长率为x,根据2021年蔬菜产量为80吨,则2022年蔬菜产量为80(1+x)吨,2023年蔬菜产量为80(1+x)(1+x)吨.预计2023年蔬菜产量达到100吨,则80(1+x)(1+x)=100,即80(1+x)2=100.
8.D 把x=3代入方程,得9-3(m+1)+2m=0,解得m=6,则原方程为x2-7x+12=0,解得x1=3,x2=4.因为这个方程的两个实数根恰好是等腰三角形ABC的两条边长,①若△ABC的腰长为4,底边长为3,则△ABC的周长为4+4+3=11;②若△ABC的腰长为3,底边长为4,则△ABC的周长为3+3+4=10.综上所述,△ABC的周长为10或11.故选D.
9.C 解不等式组得a<-3.
∵Δ=(2a-1)2-4(a-2)=2a+5,a<-3,
∴Δ=2a+5<0.
∴关于x的方程(a-2)x2-(2a-1)x+a+=0没有实数根.
10.B 利用配方法解方程x2+ax=b2,得到x+2=b2+,则方程的一个正根是x=-.根据勾股定理知道,AB=,而BD=,根据图形知道AD=AB-BD,即AD的长是方程的一个正根.故正确答案为B.
11.1.1
关于x的方程ax2+4x-2=0(a≠0)有实数根,那么Δ=42-4·a·(-2)≥0,解得a≥-2.由于a是负整数,因此a可.
13.2 根据题意,知x1+x2=3x2=3,解得x2=1.
将其代入关于x的方程x2-3x+k=0,得1-3×1+k=0,
解得k=2.
故答案是2.
14.(3+x)(4-0.5x)=15
15.8或9 当4为腰长时,将x=4代入x2-6x+n=0,得42-6×4+n=0,
解得n=8,
当n=8时,原方程为x2-6x+8=0,
解得x1=2,x2=4.
∵2+4>4,∴n=8符合题意;
当4为底边长时,关于x的方程x2-6x+n=0有两个相等的实数根,
∴Δ=(-6)2-4×1×n=0,解得n=9.
当n=9时,原方程为x2-6x+9=0,
解得x1=x2=3.
∵3+3=6>4,∴n=9符合题意.
故答案为8或9.
16.①②
17.解:(1)(x+1)(x-)=0.
(x-2)(x+1-1)=0.
x-2=0或x+1-1=0.
所以x1=2,x2=0.
(2)原方程整理得3x2+4x-1=0.
Δ=42-4×3×(-1)=28,
x==,
所以x1=,x2=.
18.解:=0,x2-2x=2,x2-2x+1=3,
(x-1)2=3,x=±+1.
∵m>0,∴m=+1.
∴=m-1=.
19.解:(1)解方程①,得x1=1,x2=2;
解方程②,得x=.
当=1时,a=2;当=2时,a=.
综上所述,a的值是2或.
(2)由题意可知1≤≤2,解得2≤a≤.
20.解:(1)证明:原方程可整理为x2-5x+4-a2=0.
∵Δ=25-4(4-a2)=4a2+9>0,
∴此方程有两个不相等的实数根.
(2)∵|a-2|=0,∴a=2.
原方程可整理为x2-5x=0.
解得x1=0,x2=5.
21.解:60,6n
画图略
(1)61 (3n2-3n+1)
(2)可能.
令3n2-3n+1=271,
则=0,
(n-10)(n+9)=0.
解得n1=10,n2=-9(舍去).
∴小圆圈的个数可能等于271,它是第10个点阵.
22.解:(1)60
(2)解法一:设每吨售价下降10x元.
由题意,可列方程(260-100-10x)(45+7.5x)=9000.
化简,得x2-10x+24=0.解得x1=4,x2=6.
所以当售价定为每吨200元或220元时,该经销店的月利润均为9000元.
当售价定为每吨200元时,月销售量更大,所以售价应定为每吨200元.
解法二:设售价定为每吨x元.
由题意,可列方程(x-100)45+×7.5=9000.
化简,得x2-420x+44000=0.
解得x1=200,x2=220.
因为要尽可能地扩大销售量,所以售价应定为每吨200元.
23.解:(1)设游泳池的宽为x米,则长为2x米.
根据题意,得
(2x+2+5+1)·(x+2+2+1+1)=1798.
整理,得x2+10x-875=0.
解得x1=-35(不合题意,舍去),x2=25.
∴2x=2×25=50.
故游泳池的长为50米,宽为25米.
(2)[(25×3+50×3)×2+25×50]×50=(450+1250)×50=1700×50=85000(元).
故共需要费用85000元.
24. (1)要使四边形PBCQ的面积是矩形ABCD面积的,此时点P应在AB上,才能构成四边形.根据“路程=速度×时间”,设两动点运动x s,分别用x表示BP,CQ的长,再根据梯形的面积公式列方程求解;
(2)根据勾股定理列方程即可,注意分情况考虑.
解:(1)设两动点运动x s后,四边形PBCQ的面积是矩形ABCD面积的,此时点P应在AB上.
根据题意,得BP=(6-2x)cm,CQ=x cm,矩形ABCD的面积是12 cm2,则有(x+6-2x)×2=12×,
解得x=.
即两动点运动 s后,四边形PBCQ的面积是矩形ABCD面积的.
(2)存在.设两动点经过t s时点P与点Q之间的距离为 cm.
①当0
②当3
综上所述,当运动 s或 s时,点P与点Q之间的距离为 cm.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
