北师大版数学九年级上册同步提优训练:第4章 图形的相似 中考真题集训(word版 含解析)
文档属性
| 名称 | 北师大版数学九年级上册同步提优训练:第4章 图形的相似 中考真题集训(word版 含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 251.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-11 00:00:00 | ||
图片预览




文档简介
图形的相似
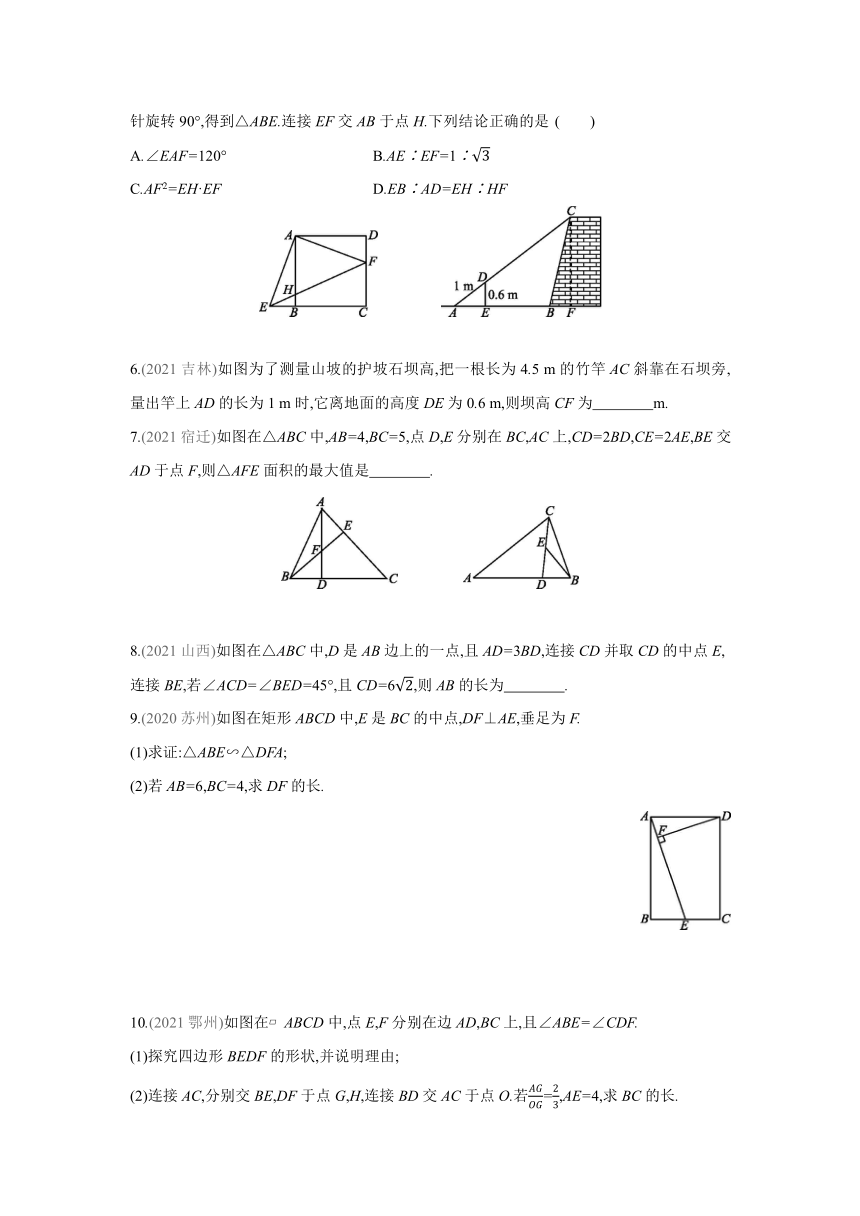
1.(2021阿坝州)如图直线l1∥l2∥l3,直线a,b与l1,l2,l3分别交于点A,B,C和点D,E,F.若AB∶BC=2∶3,EF=9,则DE的长是 ( )
A.4 B.6 C.7 D.12
2.(2021巴中)如图在△ABC中,点D,E分别在AB,AC上,且==,则下列结论正确的是 ( )
A.DE∶BC=1∶2
B.△ADE与△ABC的面积比为1∶3
C.△ADE与△ABC的周长比为1∶2
D.DE∥BC
3.(2021河北)①是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图②所示,此时液面AB的长为 ( )
A.1 cm B.2 cm C.3 cm D.4 cm
4.(2020海南)如图在 ABCD中,AB=10,AD=15,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,若BG=8,则△CEF的周长为 ( )
A.16 B.17 C.24 D.25
5.(2021大庆)如图F是线段CD上除端点外的一点,将△ADF绕正方形ABCD的顶点A顺时针旋转90°,得到△ABE.连接EF交AB于点H.下列结论正确的是 ( )
A.∠EAF=120° B.AE∶EF=1∶
C.AF2=EH·EF D.EB∶AD=EH∶HF
6.(2021吉林)如图为了测量山坡的护坡石坝高,把一根长为4.5 m的竹竿AC斜靠在石坝旁,量出竿上AD的长为1 m时,它离地面的高度DE为0.6 m,则坝高CF为 m.
7.(2021宿迁)如图在△ABC中,AB=4,BC=5,点D,E分别在BC,AC上,CD=2BD,CE=2AE,BE交AD于点F,则△AFE面积的最大值是 .
8.(2021山西)如图在△ABC中,D是AB边上的一点,且AD=3BD,连接CD并取CD的中点E,连接BE,若∠ACD=∠BED=45°,且CD=6,则AB的长为 .
9.(2020苏州)如图在矩形ABCD中,E是BC的中点,DF⊥AE,垂足为F.
(1)求证:△ABE∽△DFA;
(2)若AB=6,BC=4,求DF的长.
10.(2021鄂州)如图在 ABCD中,点E,F分别在边AD,BC上,且∠ABE=∠CDF.
(1)探究四边形BEDF的形状,并说明理由;
(2)连接AC,分别交BE,DF于点G,H,连接BD交AC于点O.若=,AE=4,求BC的长.
11.(2020杭州)如图在正方形ABCD中,点E在BC边上,连接AE,∠DAE的平分线AG与CD边交于点G,与BC的延长线交于点F.设=λ(λ>0).
(1)若AB=2,λ=1,求线段CF的长.
(2)连接EG,若EG⊥AF.
①求证:G为CD边的中点;
②求λ的值.
答案
图形的相似
1.B ∵l1∥l2∥l3,
∴AB∶BC=DE∶EF.
∵AB∶BC=2∶3,EF=9,
∴DE=6.
故选B.
2.D ∵==,
∴AD∶AB=AE∶AC=1∶3.
又∵∠A=∠A,
∴△ADE∽△ABC,
∴DE∶BC=1∶3,故A项错误;
∵△ADE∽△ABC,
∴△ADE与△ABC的面积比为1∶9,周长比为1∶3,故B项和C项错误;
∵△ADE∽△ABC,
∴∠ADE=∠B,
∴DE∥BC,故D项正确.
故选D.
3.C 如图,过点O作OM⊥CD,垂足为M,过点O'作O'N⊥AB,垂足为N.
∵CD∥AB,
∴△CDO∽△ABO',
∴=.
∵OM=15-7=8(cm),O'N=11-7=4(cm),
∴=,
∴AB=3 cm.
故选C.
4.A ∵在 ABCD中,CD=AB=10,BC=AD=15,∠BAD的平分线交BC于点E,
∴AB∥DC,∠BAF=∠DAF,
∴∠BAF=∠F,
∴∠DAF=∠F,
∴DF=AD=15.
同理BE=AB=10,
∴CF=DF-CD=15-10=5.
在△ABG中,BG⊥AE,AB=10,BG=8,
∴AG===6,
易得AE=2AG=12,
∴△ABE的周长等于10+10+12=32.
∵AB∥CF,
∴△CEF∽△BEA,
∴相似比为CF∶AB=5∶10=1∶2,
∴△CEF的周长为16.
故选A.
5.D ∵△ADF绕正方形ABCD的顶点A顺时针旋转90°,得到△ABE,
∴△ABE≌△ADF,
∴∠BAE=∠DAF,
∴∠EAF=∠BAE+∠FAB=∠DAF+∠FAB=90°,
故A项不正确;
∵∠EAF=90°,AE=AF,
∴△AEF是等腰直角三角形,
∴EF=AE,
∴AE∶EF=1∶,
故B项不正确;
若AF2=EH·EF成立,
∵AE∶EF=1∶,AE=AF,
∴EH=AF,
∴EH=EF,
即H是EF的中点.而H不一定是EF的中点,
故C项不正确;
∵AB∥CD,
∴EB∶BC=EH∶HF.
∵BC=AD,
∴EB∶AD=EH∶HF,
故D项正确.
故选D.
6.2.7 由题易知DE∥CF,
∴△ADE∽△ACF,
∴=,即=,
解得CF=2.7(m).
故答案为2.7.
7. 如图,连接DE.
∵CD=2BD,CE=2AE,
∴==.
又∵∠C=∠C,∴△CDE∽△CBA,
则==,∠CDE=∠CBA,
∴AB∥DE,
∴△ABF∽△DEF,
∴==.
∵DE∥AB,
∴S△ABE=S△ABD,
∴S△AEF=S△BDF,
∴S△AEF=S△ABD.
∵BD=BC=,
∴当AB⊥BD时,△ABD的面积最大,最大值为××4=,
∴△AFE的面积的最大值=×=.
8.4 如图,取AD的中点F,连接EF,过点D作DG⊥EF于点G,DH⊥BE于点H.
设BD=a,
∴AD=3BD=3a,AB=4a.
∵E为CD的中点,F为AD的中点,CD=6,
∴DF=a,EF∥AC,DE=3,
∴∠FED=∠ACD=45°.
又∵∠BED=45°,
∴∠FEB=90°.
又∵DG⊥EF,DH⊥BE,
∴四边形EHDG是正方形,
则DE=DG,DH∥EF,
∴DG=DH=3.
∵DH∥EF,
∴∠BDH=∠DFG,
∴△BDH∽△DFG,
∴=,
则=,
∴BH=2,
∴BD===,
∴AB=4.
故答案为4.
9.解:(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,
∴∠DAF=∠AEB.
∵DF⊥AE,
∴∠AFD=∠B=90°,
∴△ABE∽△DFA.
(2)∵E是BC的中点,BC=4,
∴BE=2.
∵AB=6,
∴AE===2.
∵四边形ABCD是矩形,
∴AD=BC=4.
∵△ABE∽△DFA,
∴=,
∴DF===.
10.解:(1)四边形BEDF为平行四边形.理由如下:
∵四边形ABCD为平行四边形,
∴AD∥BC,∠ABC=∠ADC,
∴∠EDF=∠DFC.
∵∠ABE=∠CDF,
∴∠EBF=∠EDF.
∴∠DFC=∠EBC,
∴BE∥DF.
又∵AD∥BC,
∴四边形BEDF为平行四边形.
(2)设AG=2a.∵=,
∴OG=3a,AO=5a.
∵四边形ABCD为平行四边形,
∴AO=CO=5a,
∴CG=8a.
∵AD∥BC,
∴△AGE∽△CGB,
∴==.
∵AE=4,
∴BC=16.
11.解:∵在正方形ABCD中,AD∥BC,
∴∠DAG=∠F.
∵AG平分∠DAE,
∴∠DAG=∠EAG,
∴∠EAG=∠F,
∴EA=EF.
(1)∵BC=AB=2,E为BC的中点,
∴BE=EC=1,
∴AE==,
∴EF=,
则CF=EF-EC=-1.
(2)①证明:∵EA=EF,EG⊥AF,
∴AG=FG.
在△ADG和△FCG中,∵∠D=∠GCF=90°,∠AGD=∠FGC,AG=FG,
∴△ADG≌△FCG(AAS),
∴DG=CG,
即G为CD的中点.
②设CD=2a,则CG=a.
∵△ADG≌△FCG,∴CF=DA=2a.
∵EG⊥AF,∠GCF=90°,
∴∠EGC+∠CGF=90°,∠F+∠CGF=90°,
∴∠EGC=∠F.
又∵∠ECG=∠GCF=90°,
∴△EGC∽△GFC,
∴=.
∵GC=a,FC=2a,
∴==,
∴EC=a,
∴BE=BC-EC=2a-a=a,
则λ===.
1.(2021阿坝州)如图直线l1∥l2∥l3,直线a,b与l1,l2,l3分别交于点A,B,C和点D,E,F.若AB∶BC=2∶3,EF=9,则DE的长是 ( )
A.4 B.6 C.7 D.12
2.(2021巴中)如图在△ABC中,点D,E分别在AB,AC上,且==,则下列结论正确的是 ( )
A.DE∶BC=1∶2
B.△ADE与△ABC的面积比为1∶3
C.△ADE与△ABC的周长比为1∶2
D.DE∥BC
3.(2021河北)①是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图②所示,此时液面AB的长为 ( )
A.1 cm B.2 cm C.3 cm D.4 cm
4.(2020海南)如图在 ABCD中,AB=10,AD=15,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,若BG=8,则△CEF的周长为 ( )
A.16 B.17 C.24 D.25
5.(2021大庆)如图F是线段CD上除端点外的一点,将△ADF绕正方形ABCD的顶点A顺时针旋转90°,得到△ABE.连接EF交AB于点H.下列结论正确的是 ( )
A.∠EAF=120° B.AE∶EF=1∶
C.AF2=EH·EF D.EB∶AD=EH∶HF
6.(2021吉林)如图为了测量山坡的护坡石坝高,把一根长为4.5 m的竹竿AC斜靠在石坝旁,量出竿上AD的长为1 m时,它离地面的高度DE为0.6 m,则坝高CF为 m.
7.(2021宿迁)如图在△ABC中,AB=4,BC=5,点D,E分别在BC,AC上,CD=2BD,CE=2AE,BE交AD于点F,则△AFE面积的最大值是 .
8.(2021山西)如图在△ABC中,D是AB边上的一点,且AD=3BD,连接CD并取CD的中点E,连接BE,若∠ACD=∠BED=45°,且CD=6,则AB的长为 .
9.(2020苏州)如图在矩形ABCD中,E是BC的中点,DF⊥AE,垂足为F.
(1)求证:△ABE∽△DFA;
(2)若AB=6,BC=4,求DF的长.
10.(2021鄂州)如图在 ABCD中,点E,F分别在边AD,BC上,且∠ABE=∠CDF.
(1)探究四边形BEDF的形状,并说明理由;
(2)连接AC,分别交BE,DF于点G,H,连接BD交AC于点O.若=,AE=4,求BC的长.
11.(2020杭州)如图在正方形ABCD中,点E在BC边上,连接AE,∠DAE的平分线AG与CD边交于点G,与BC的延长线交于点F.设=λ(λ>0).
(1)若AB=2,λ=1,求线段CF的长.
(2)连接EG,若EG⊥AF.
①求证:G为CD边的中点;
②求λ的值.
答案
图形的相似
1.B ∵l1∥l2∥l3,
∴AB∶BC=DE∶EF.
∵AB∶BC=2∶3,EF=9,
∴DE=6.
故选B.
2.D ∵==,
∴AD∶AB=AE∶AC=1∶3.
又∵∠A=∠A,
∴△ADE∽△ABC,
∴DE∶BC=1∶3,故A项错误;
∵△ADE∽△ABC,
∴△ADE与△ABC的面积比为1∶9,周长比为1∶3,故B项和C项错误;
∵△ADE∽△ABC,
∴∠ADE=∠B,
∴DE∥BC,故D项正确.
故选D.
3.C 如图,过点O作OM⊥CD,垂足为M,过点O'作O'N⊥AB,垂足为N.
∵CD∥AB,
∴△CDO∽△ABO',
∴=.
∵OM=15-7=8(cm),O'N=11-7=4(cm),
∴=,
∴AB=3 cm.
故选C.
4.A ∵在 ABCD中,CD=AB=10,BC=AD=15,∠BAD的平分线交BC于点E,
∴AB∥DC,∠BAF=∠DAF,
∴∠BAF=∠F,
∴∠DAF=∠F,
∴DF=AD=15.
同理BE=AB=10,
∴CF=DF-CD=15-10=5.
在△ABG中,BG⊥AE,AB=10,BG=8,
∴AG===6,
易得AE=2AG=12,
∴△ABE的周长等于10+10+12=32.
∵AB∥CF,
∴△CEF∽△BEA,
∴相似比为CF∶AB=5∶10=1∶2,
∴△CEF的周长为16.
故选A.
5.D ∵△ADF绕正方形ABCD的顶点A顺时针旋转90°,得到△ABE,
∴△ABE≌△ADF,
∴∠BAE=∠DAF,
∴∠EAF=∠BAE+∠FAB=∠DAF+∠FAB=90°,
故A项不正确;
∵∠EAF=90°,AE=AF,
∴△AEF是等腰直角三角形,
∴EF=AE,
∴AE∶EF=1∶,
故B项不正确;
若AF2=EH·EF成立,
∵AE∶EF=1∶,AE=AF,
∴EH=AF,
∴EH=EF,
即H是EF的中点.而H不一定是EF的中点,
故C项不正确;
∵AB∥CD,
∴EB∶BC=EH∶HF.
∵BC=AD,
∴EB∶AD=EH∶HF,
故D项正确.
故选D.
6.2.7 由题易知DE∥CF,
∴△ADE∽△ACF,
∴=,即=,
解得CF=2.7(m).
故答案为2.7.
7. 如图,连接DE.
∵CD=2BD,CE=2AE,
∴==.
又∵∠C=∠C,∴△CDE∽△CBA,
则==,∠CDE=∠CBA,
∴AB∥DE,
∴△ABF∽△DEF,
∴==.
∵DE∥AB,
∴S△ABE=S△ABD,
∴S△AEF=S△BDF,
∴S△AEF=S△ABD.
∵BD=BC=,
∴当AB⊥BD时,△ABD的面积最大,最大值为××4=,
∴△AFE的面积的最大值=×=.
8.4 如图,取AD的中点F,连接EF,过点D作DG⊥EF于点G,DH⊥BE于点H.
设BD=a,
∴AD=3BD=3a,AB=4a.
∵E为CD的中点,F为AD的中点,CD=6,
∴DF=a,EF∥AC,DE=3,
∴∠FED=∠ACD=45°.
又∵∠BED=45°,
∴∠FEB=90°.
又∵DG⊥EF,DH⊥BE,
∴四边形EHDG是正方形,
则DE=DG,DH∥EF,
∴DG=DH=3.
∵DH∥EF,
∴∠BDH=∠DFG,
∴△BDH∽△DFG,
∴=,
则=,
∴BH=2,
∴BD===,
∴AB=4.
故答案为4.
9.解:(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,
∴∠DAF=∠AEB.
∵DF⊥AE,
∴∠AFD=∠B=90°,
∴△ABE∽△DFA.
(2)∵E是BC的中点,BC=4,
∴BE=2.
∵AB=6,
∴AE===2.
∵四边形ABCD是矩形,
∴AD=BC=4.
∵△ABE∽△DFA,
∴=,
∴DF===.
10.解:(1)四边形BEDF为平行四边形.理由如下:
∵四边形ABCD为平行四边形,
∴AD∥BC,∠ABC=∠ADC,
∴∠EDF=∠DFC.
∵∠ABE=∠CDF,
∴∠EBF=∠EDF.
∴∠DFC=∠EBC,
∴BE∥DF.
又∵AD∥BC,
∴四边形BEDF为平行四边形.
(2)设AG=2a.∵=,
∴OG=3a,AO=5a.
∵四边形ABCD为平行四边形,
∴AO=CO=5a,
∴CG=8a.
∵AD∥BC,
∴△AGE∽△CGB,
∴==.
∵AE=4,
∴BC=16.
11.解:∵在正方形ABCD中,AD∥BC,
∴∠DAG=∠F.
∵AG平分∠DAE,
∴∠DAG=∠EAG,
∴∠EAG=∠F,
∴EA=EF.
(1)∵BC=AB=2,E为BC的中点,
∴BE=EC=1,
∴AE==,
∴EF=,
则CF=EF-EC=-1.
(2)①证明:∵EA=EF,EG⊥AF,
∴AG=FG.
在△ADG和△FCG中,∵∠D=∠GCF=90°,∠AGD=∠FGC,AG=FG,
∴△ADG≌△FCG(AAS),
∴DG=CG,
即G为CD的中点.
②设CD=2a,则CG=a.
∵△ADG≌△FCG,∴CF=DA=2a.
∵EG⊥AF,∠GCF=90°,
∴∠EGC+∠CGF=90°,∠F+∠CGF=90°,
∴∠EGC=∠F.
又∵∠ECG=∠GCF=90°,
∴△EGC∽△GFC,
∴=.
∵GC=a,FC=2a,
∴==,
∴EC=a,
∴BE=BC-EC=2a-a=a,
则λ===.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
