北师大版(新)八上-1.2 一定是直角三角形吗【优质课件】
文档属性
| 名称 | 北师大版(新)八上-1.2 一定是直角三角形吗【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览











文档简介
(共34张PPT)
1.2 一定是直角三角形吗
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
问题1:在一个直角三角形中三条边满足什么样的关系呢?
答:在一个直角三角形中两直角边的平方和等于斜边的平方.
问题2:如果一个三角形中有两边的平方和等于第三边的平方,那么这个三角形是否就是直角三角形呢?
新课精讲
探索新知
1
知识点
由三边关系确定直角三角形
做一做
下面的每组数分别是一个三角形的三边长a,b,c 而且都满足a2+b2=c2:3,4,5;5,12,13;8,15,17;7,24,25.
分别以每组数为三边长画出三角形,它们都是直角三角形吗?你是怎么想的?与同伴进行交流.
探索新知
直角三角形的判定:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
2.利用边的关系判定直角三角形的步骤:
(1)比较三边长a,b,c的大小,找出最长边.
(2)计算两短边的平方和,看它是否与最长边的平方相等;若相等,则是直角三角形,且最长边所对的角是直角;若不相等,则此三角形不是直角三角形.
探索新知
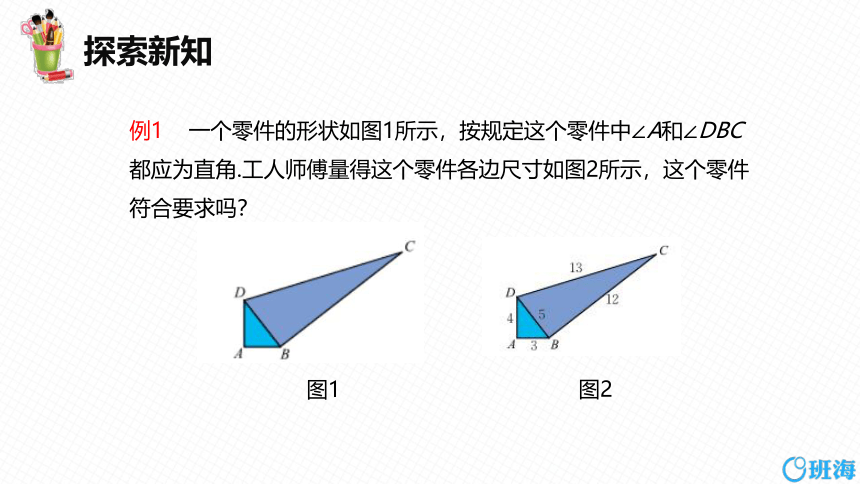
例1 一个零件的形状如图1所示,按规定这个零件中∠A和∠DBC都应为直角.工人师傅量得这个零件各边尺寸如图2所示,这个零件符合要求吗?
图2
图1
探索新知
解:在△ABD中,AB 2+AD 2=9+16=25=BD 2,
所以△ABD是直角三角形,∠A是直角.
在△BCD中,BD 2+BC 2=25+144=169=CD 2,
所以△BCD是直角三角形,∠DBC是直角.
因此,这个零件符合要求.
探索新知
例2 判断满足下列条件的三角形是不是直角三角形:
(1)在△ABC中,∠A=25°,∠C=65°;
(2)在△ABC中,AC=12,AB=20,BC=16;
(3)一个三角形的三边长a,b,c满足b2-a2=c2.
导引:判断一个三角形是不是直角三角形,如果条件与角 相关,则考虑用定义判断,如果条件与边相关,则考虑用边的关系判断.第(1)题可以直接根据直角三角形的定义判断;第(2)(3)题可以依据边的关系判断.
探索新知
解:(1)在△ABC中,因为∠A+∠B+∠C=180°,
所以∠B=180°-25°-65°=90°.
所以△ABC是直角三角形.
(2)在△ABC中,因为AC2+BC2=122+162=202=AB2,
所以△ABC是直角三角形,且∠C为直角.
(3)因为三角形的三边长满足b2-a2=c2,即b2=a2+c2,
所以此三角形是直角三角形,且b是斜边长.
警示:判断一个三角形的形状时,除考虑是否为直角三角形外,还要考虑是否为等腰三角形.
探索新知
总 结
判断一个三角形是不是直角三角形有两种方法:
(1)利用定义,即如果已知条件与角度有关,可借助三角形的内角和判断;
(2)利用直角三角形的判定条件,即若已知条件与边有关,一般通过计算得出三边的数量关系来判断,看是否符合较短两边的平方和等于最长边的平方.
典题精讲
下列四组线段中,能组成直角三角形的是( )
A.a=1,b=2,c=3 B.a=2,b=3,c=4
C.a=2,b=4,c=5 D.a=3,b=4,c=5
1
D
2 如图,每个小正方形的边长均为1,则△ABC是( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等腰三角形
A
探索新知
2
知识点
勾股数
1. 勾股数:满足a2+b2=c2的三个正整数,称为勾股数.常见的勾股数有:3,4,5;5,12,13;8,15,17;7,24,25;9,40,41;….
探索新知
2.判断勾股数的方法:
(1)确定是不是三个正整数;
(2)确定最大数;
(3)计算:看较小两数的平方和是否等于最大数的平方.
3.易错警示:勾股数必须同时满足两个条件:
(1)三个数都是正整数;
(2)两个较小数的平方和等于最大数的平方.
探索新知
例3 下面四组数中是勾股数的一组是( )
A.6,7,8 B.5,8,13
C.1.5,2,2.5 D.21,28,35
导引:根据勾股数的定义:满足a2+b2=c2的三个正整数a,b,c称为勾股数.
A.62+72≠82,不是勾股数,故错误;
B.52+82≠132,不是勾股数,故错误;
C.1.5和2.5不是整数,所以不是勾股数,故错误;
D.212+282=352,是勾股数,故正确.
D
探索新知
总 结
确定勾股数的方法:
首先看这三个数是不是正整数;然后看较小两个数的平方和是否等于最大数的平方.记住常见的勾股数(3,4,5;5,12,13;8,15,17;7,24,25)可以提高解题速度.
探索新知
例4 观察下面的表格所给出的三个数a,b,c,其中a<b<c.
(1)试找出它们的共同点,并说明你的结论;
(2)当a=21时,求b,c的值.
3,4,5 32+42=52
5,12,13 52+122=132
7,24,25 72+242=252
9,40,41 92+402=412
… …
a,b,c a2+b2=c2
探索新知
导引:只要能够发现每组三个数之间的规律即可,这就需从不同的角度去观察、分析,运用从特殊到一般的思想来解答.
解: (1)各组数的共同点:
①各组数均满足a2+b2=c2;
②最小数a是奇数,其余的两个数b,c是连续的正整数;
③最小奇数的平方等于另外两个连续正整数的和.
探索新知
由以上特点可猜想并说明这样一个结论:
设x为大于1的奇数,将x2拆分为两个连续正整数之和,
即x2=y+(y+1),则x,y,y+1就能构成一组勾股数.
理由:因为x2=y+(y+1)(x为大于1的奇数),
所以x2+y2=y+(y+1)+y2=y2+2y+1=(y+1)2.
所以x,y,y+1是一组勾股数.
(2)运用以上结论,当a=21时,212=441=220+221.
所以b=220,c=221.
探索新知
总 结
寻找与大于且等于3的奇数组成勾股数的一种方法:
先选一个大于1的奇数,然后把这个数的平方写成两个连续正整数的和,则这个奇数和分成的两个连续正整数就构成了一组勾股数,如452=2 025=1 012+1 013,则45,1 012,1 013就是一组勾股数,运用此法可以得到许多组勾股数.
典题精讲
下列各组数中,不是勾股数的是( )
A.5,12,13
B.7,24,25
C.8,12,15
D.3k,4k,5k(k为正整数)
C
学以致用
小试牛刀
1.如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是____________.
直角三角形
2.满足a2+b2=c2的三个正整数,称为____________.
3.下列各组数能构成勾股数的是________(填序号).
① 6,8,10;② 7,8,10;③ , ,1.
勾股数
①
小试牛刀
4.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且(a+b)(a-b)=c2,则( )
A.∠A为直角 B.∠C为直角
C.∠B为直角 D.△ABC不是直角三角形
A
5.下列长度的三条线段能组成钝角三角形的是( )
A.3,4,4 B.3,4,5
C.3,4,6 D.3,4,7
C
小试牛刀
6.下列各组数中,是勾股数的是( )
A.14,36,39 B.8,24,25
C.8,15,17 D.10,20,26
C
7.下列几组数:
①9,12,15;②8,15,17;③7,24,25;
④n2-1,2n,n2+1(n是大于1的整数).
其中是勾股数的有( )
A.1组 B.2组 C.3组 D.4组
D
小试牛刀
7.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,如果a= ,b= ,c=2,这个三角形是直角三角形吗?请说明理由.
小利的解答如下:
解:这个三角形不是直角三角形.理由如下:
因为a2+b2= 2+ 2= ,c2=4,
所以a2+b2≠c2.
所以△ABC不是直角三角形.
请问小利的解答正确吗?若不正确,请给出正确的解答过程,并画出这个三角形.
小试牛刀
解:
小利的解答不正确.正确的解答过程如下:
这个三角形是直角三角形.理由如下:
因为 >2> ,
所以b是这个三角形的最长边.
因为a2+c2= 2+22= ,b2= 2= ,
所以a2+c2=b2.
所以△ABC是直角三角形.
画出的△ABC如图所示.
小试牛刀
8.如图,在四边形ABCD中,AB=BC=2,CD=3,AD=1,且∠B=90°.求∠BAD的度数.
连接AC. 因为∠B=90°,AB=BC=2,
所以△ABC为等腰直角三角形. 所以∠BAC=45°.
又因为CD=3,AD=1,
所以AC2+AD2=AB2+BC2+AD2=4+4+1=9,
CD2=9.
解:
所以AC2+AD2=CD2.
所以△ACD是直角三角形且∠CAD=90°.
所以∠BAD=45°+90°=135°.
小试牛刀
9.如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=3,PB=1,PC=2.求∠BPC的度数.
【思路点拨】解答本题要紧扣两个切入点:
(1)由于∠BPC是一钝角,想办法将其分割成一直角与一特殊角(30°,60°,45°)的和的形式;
(2)用旋转法将△CPB绕点C顺时针旋转90°到△CP′A的位置.
小试牛刀
解:
如图,将△CPB绕点C顺时针旋转90°得△CP′A,则P′C=PC=2,P′A=PB=1,∠BPC=∠AP′C,连接PP′.
∵∠PCP′=90°,∴PP′2=22+22=8.
∵P′A=1,PA=3,
∴PP′2+P′A2=8+1=9,PA2=9.
∴PP′2+P′A2=PA2. ∴∠AP′P=90°.
易知∠CP′P=45°,
∴∠BPC=∠AP′C=∠AP′P+∠CP′P
=90°+45°=135°.
课堂小结
课堂小结
1.如果三角形的三边长a,b,c满足a2 +b2=c2,那么这个三角形是直角三角形.
2.勾股数:满足a2 +b2=c2的三个正整数,称为勾股数.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
1.2 一定是直角三角形吗
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
问题1:在一个直角三角形中三条边满足什么样的关系呢?
答:在一个直角三角形中两直角边的平方和等于斜边的平方.
问题2:如果一个三角形中有两边的平方和等于第三边的平方,那么这个三角形是否就是直角三角形呢?
新课精讲
探索新知
1
知识点
由三边关系确定直角三角形
做一做
下面的每组数分别是一个三角形的三边长a,b,c 而且都满足a2+b2=c2:3,4,5;5,12,13;8,15,17;7,24,25.
分别以每组数为三边长画出三角形,它们都是直角三角形吗?你是怎么想的?与同伴进行交流.
探索新知
直角三角形的判定:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
2.利用边的关系判定直角三角形的步骤:
(1)比较三边长a,b,c的大小,找出最长边.
(2)计算两短边的平方和,看它是否与最长边的平方相等;若相等,则是直角三角形,且最长边所对的角是直角;若不相等,则此三角形不是直角三角形.
探索新知
例1 一个零件的形状如图1所示,按规定这个零件中∠A和∠DBC都应为直角.工人师傅量得这个零件各边尺寸如图2所示,这个零件符合要求吗?
图2
图1
探索新知
解:在△ABD中,AB 2+AD 2=9+16=25=BD 2,
所以△ABD是直角三角形,∠A是直角.
在△BCD中,BD 2+BC 2=25+144=169=CD 2,
所以△BCD是直角三角形,∠DBC是直角.
因此,这个零件符合要求.
探索新知
例2 判断满足下列条件的三角形是不是直角三角形:
(1)在△ABC中,∠A=25°,∠C=65°;
(2)在△ABC中,AC=12,AB=20,BC=16;
(3)一个三角形的三边长a,b,c满足b2-a2=c2.
导引:判断一个三角形是不是直角三角形,如果条件与角 相关,则考虑用定义判断,如果条件与边相关,则考虑用边的关系判断.第(1)题可以直接根据直角三角形的定义判断;第(2)(3)题可以依据边的关系判断.
探索新知
解:(1)在△ABC中,因为∠A+∠B+∠C=180°,
所以∠B=180°-25°-65°=90°.
所以△ABC是直角三角形.
(2)在△ABC中,因为AC2+BC2=122+162=202=AB2,
所以△ABC是直角三角形,且∠C为直角.
(3)因为三角形的三边长满足b2-a2=c2,即b2=a2+c2,
所以此三角形是直角三角形,且b是斜边长.
警示:判断一个三角形的形状时,除考虑是否为直角三角形外,还要考虑是否为等腰三角形.
探索新知
总 结
判断一个三角形是不是直角三角形有两种方法:
(1)利用定义,即如果已知条件与角度有关,可借助三角形的内角和判断;
(2)利用直角三角形的判定条件,即若已知条件与边有关,一般通过计算得出三边的数量关系来判断,看是否符合较短两边的平方和等于最长边的平方.
典题精讲
下列四组线段中,能组成直角三角形的是( )
A.a=1,b=2,c=3 B.a=2,b=3,c=4
C.a=2,b=4,c=5 D.a=3,b=4,c=5
1
D
2 如图,每个小正方形的边长均为1,则△ABC是( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等腰三角形
A
探索新知
2
知识点
勾股数
1. 勾股数:满足a2+b2=c2的三个正整数,称为勾股数.常见的勾股数有:3,4,5;5,12,13;8,15,17;7,24,25;9,40,41;….
探索新知
2.判断勾股数的方法:
(1)确定是不是三个正整数;
(2)确定最大数;
(3)计算:看较小两数的平方和是否等于最大数的平方.
3.易错警示:勾股数必须同时满足两个条件:
(1)三个数都是正整数;
(2)两个较小数的平方和等于最大数的平方.
探索新知
例3 下面四组数中是勾股数的一组是( )
A.6,7,8 B.5,8,13
C.1.5,2,2.5 D.21,28,35
导引:根据勾股数的定义:满足a2+b2=c2的三个正整数a,b,c称为勾股数.
A.62+72≠82,不是勾股数,故错误;
B.52+82≠132,不是勾股数,故错误;
C.1.5和2.5不是整数,所以不是勾股数,故错误;
D.212+282=352,是勾股数,故正确.
D
探索新知
总 结
确定勾股数的方法:
首先看这三个数是不是正整数;然后看较小两个数的平方和是否等于最大数的平方.记住常见的勾股数(3,4,5;5,12,13;8,15,17;7,24,25)可以提高解题速度.
探索新知
例4 观察下面的表格所给出的三个数a,b,c,其中a<b<c.
(1)试找出它们的共同点,并说明你的结论;
(2)当a=21时,求b,c的值.
3,4,5 32+42=52
5,12,13 52+122=132
7,24,25 72+242=252
9,40,41 92+402=412
… …
a,b,c a2+b2=c2
探索新知
导引:只要能够发现每组三个数之间的规律即可,这就需从不同的角度去观察、分析,运用从特殊到一般的思想来解答.
解: (1)各组数的共同点:
①各组数均满足a2+b2=c2;
②最小数a是奇数,其余的两个数b,c是连续的正整数;
③最小奇数的平方等于另外两个连续正整数的和.
探索新知
由以上特点可猜想并说明这样一个结论:
设x为大于1的奇数,将x2拆分为两个连续正整数之和,
即x2=y+(y+1),则x,y,y+1就能构成一组勾股数.
理由:因为x2=y+(y+1)(x为大于1的奇数),
所以x2+y2=y+(y+1)+y2=y2+2y+1=(y+1)2.
所以x,y,y+1是一组勾股数.
(2)运用以上结论,当a=21时,212=441=220+221.
所以b=220,c=221.
探索新知
总 结
寻找与大于且等于3的奇数组成勾股数的一种方法:
先选一个大于1的奇数,然后把这个数的平方写成两个连续正整数的和,则这个奇数和分成的两个连续正整数就构成了一组勾股数,如452=2 025=1 012+1 013,则45,1 012,1 013就是一组勾股数,运用此法可以得到许多组勾股数.
典题精讲
下列各组数中,不是勾股数的是( )
A.5,12,13
B.7,24,25
C.8,12,15
D.3k,4k,5k(k为正整数)
C
学以致用
小试牛刀
1.如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是____________.
直角三角形
2.满足a2+b2=c2的三个正整数,称为____________.
3.下列各组数能构成勾股数的是________(填序号).
① 6,8,10;② 7,8,10;③ , ,1.
勾股数
①
小试牛刀
4.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且(a+b)(a-b)=c2,则( )
A.∠A为直角 B.∠C为直角
C.∠B为直角 D.△ABC不是直角三角形
A
5.下列长度的三条线段能组成钝角三角形的是( )
A.3,4,4 B.3,4,5
C.3,4,6 D.3,4,7
C
小试牛刀
6.下列各组数中,是勾股数的是( )
A.14,36,39 B.8,24,25
C.8,15,17 D.10,20,26
C
7.下列几组数:
①9,12,15;②8,15,17;③7,24,25;
④n2-1,2n,n2+1(n是大于1的整数).
其中是勾股数的有( )
A.1组 B.2组 C.3组 D.4组
D
小试牛刀
7.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,如果a= ,b= ,c=2,这个三角形是直角三角形吗?请说明理由.
小利的解答如下:
解:这个三角形不是直角三角形.理由如下:
因为a2+b2= 2+ 2= ,c2=4,
所以a2+b2≠c2.
所以△ABC不是直角三角形.
请问小利的解答正确吗?若不正确,请给出正确的解答过程,并画出这个三角形.
小试牛刀
解:
小利的解答不正确.正确的解答过程如下:
这个三角形是直角三角形.理由如下:
因为 >2> ,
所以b是这个三角形的最长边.
因为a2+c2= 2+22= ,b2= 2= ,
所以a2+c2=b2.
所以△ABC是直角三角形.
画出的△ABC如图所示.
小试牛刀
8.如图,在四边形ABCD中,AB=BC=2,CD=3,AD=1,且∠B=90°.求∠BAD的度数.
连接AC. 因为∠B=90°,AB=BC=2,
所以△ABC为等腰直角三角形. 所以∠BAC=45°.
又因为CD=3,AD=1,
所以AC2+AD2=AB2+BC2+AD2=4+4+1=9,
CD2=9.
解:
所以AC2+AD2=CD2.
所以△ACD是直角三角形且∠CAD=90°.
所以∠BAD=45°+90°=135°.
小试牛刀
9.如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=3,PB=1,PC=2.求∠BPC的度数.
【思路点拨】解答本题要紧扣两个切入点:
(1)由于∠BPC是一钝角,想办法将其分割成一直角与一特殊角(30°,60°,45°)的和的形式;
(2)用旋转法将△CPB绕点C顺时针旋转90°到△CP′A的位置.
小试牛刀
解:
如图,将△CPB绕点C顺时针旋转90°得△CP′A,则P′C=PC=2,P′A=PB=1,∠BPC=∠AP′C,连接PP′.
∵∠PCP′=90°,∴PP′2=22+22=8.
∵P′A=1,PA=3,
∴PP′2+P′A2=8+1=9,PA2=9.
∴PP′2+P′A2=PA2. ∴∠AP′P=90°.
易知∠CP′P=45°,
∴∠BPC=∠AP′C=∠AP′P+∠CP′P
=90°+45°=135°.
课堂小结
课堂小结
1.如果三角形的三边长a,b,c满足a2 +b2=c2,那么这个三角形是直角三角形.
2.勾股数:满足a2 +b2=c2的三个正整数,称为勾股数.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
