北师大版数学九年级上册同步提优训练:第5章 投影与视图 单元综合提升卷(word版 含解析)
文档属性
| 名称 | 北师大版数学九年级上册同步提优训练:第5章 投影与视图 单元综合提升卷(word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 380.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-11 21:13:25 | ||
图片预览


文档简介
第五章综合提升卷
第Ⅰ卷 (选择题 共30分)
一、选择题(每小题3分,共30分)
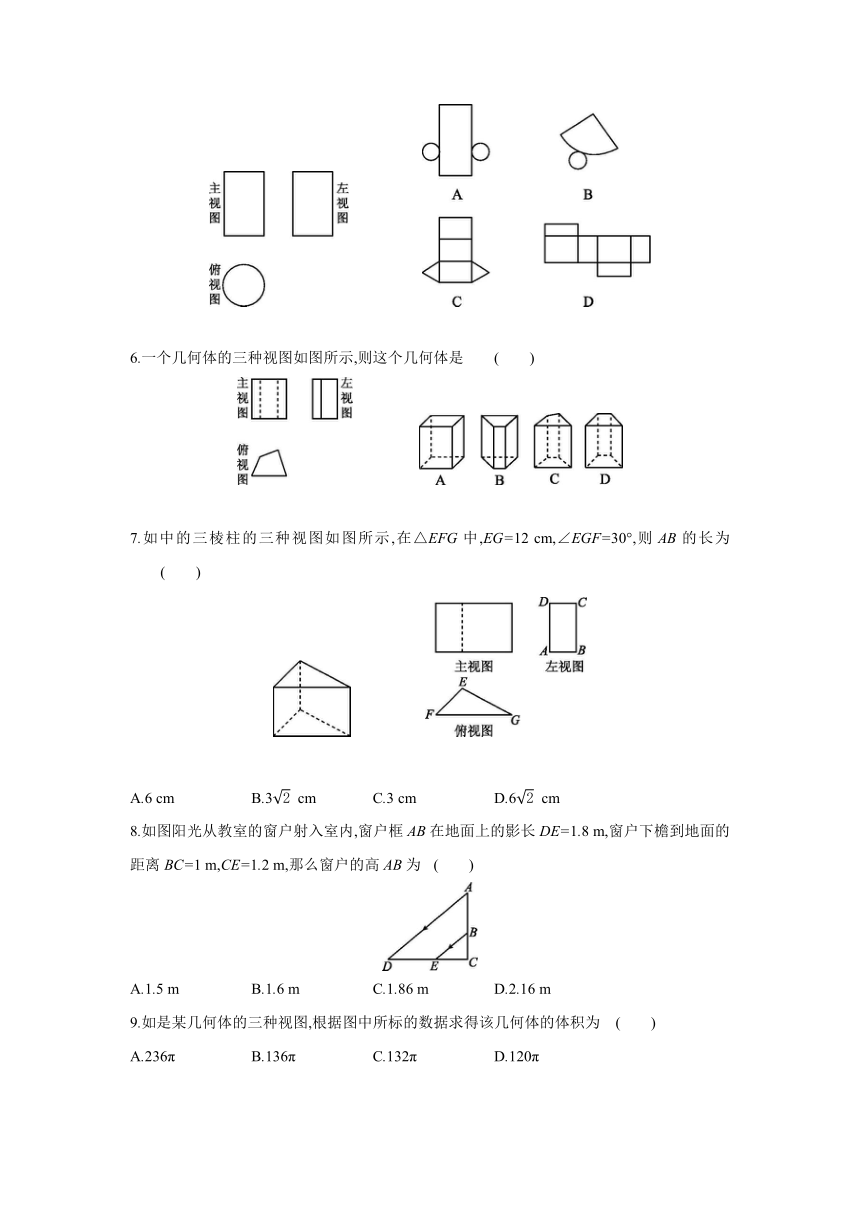
1.有两根电线杆在地面上形成了各自的影子,若以电线杆与其影子分别作为三角形的两边,可以得到两个全等三角形,则这种投影现象为 ( )
A.平行投影
B.中心投影
C.既不是平行投影也不是中心投影
D.可能是平行投影也可能是中心投影
2. 如图所示四幅图是两个物体不同时刻在太阳光下的影子,按照时间先后顺序排列正确的是 ( )
A.a→b→c→d B.d→b→c→a
C.c→d→a→b D.a→c→b→d
3.如是由5块完全相同的小正方体所搭成的几何体的俯视图,小正方形中的数字表示在该位置处小正方体的个数,则该几何体的主视图是 ( )
4.如图所示的支架(一种小零件)的两个台阶的高度和宽度相等,则它的左视图为
( )
5.如是一个几何体的三种视图,则该几何体的展开图可以是 ( )
6.一个几何体的三种视图如图所示,则这个几何体是 ( )
7.如中的三棱柱的三种视图如图所示,在△EFG中,EG=12 cm,∠EGF=30°,则AB的长为 ( )
A.6 cm B.3 cm C.3 cm D.6 cm
8.如图阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8 m,窗户下檐到地面的距离BC=1 m,CE=1.2 m,那么窗户的高AB为 ( )
A.1.5 m B.1.6 m C.1.86 m D.2.16 m
9.如是某几何体的三种视图,根据图中所标的数据求得该几何体的体积为 ( )
A.236π B.136π C.132π D.120π
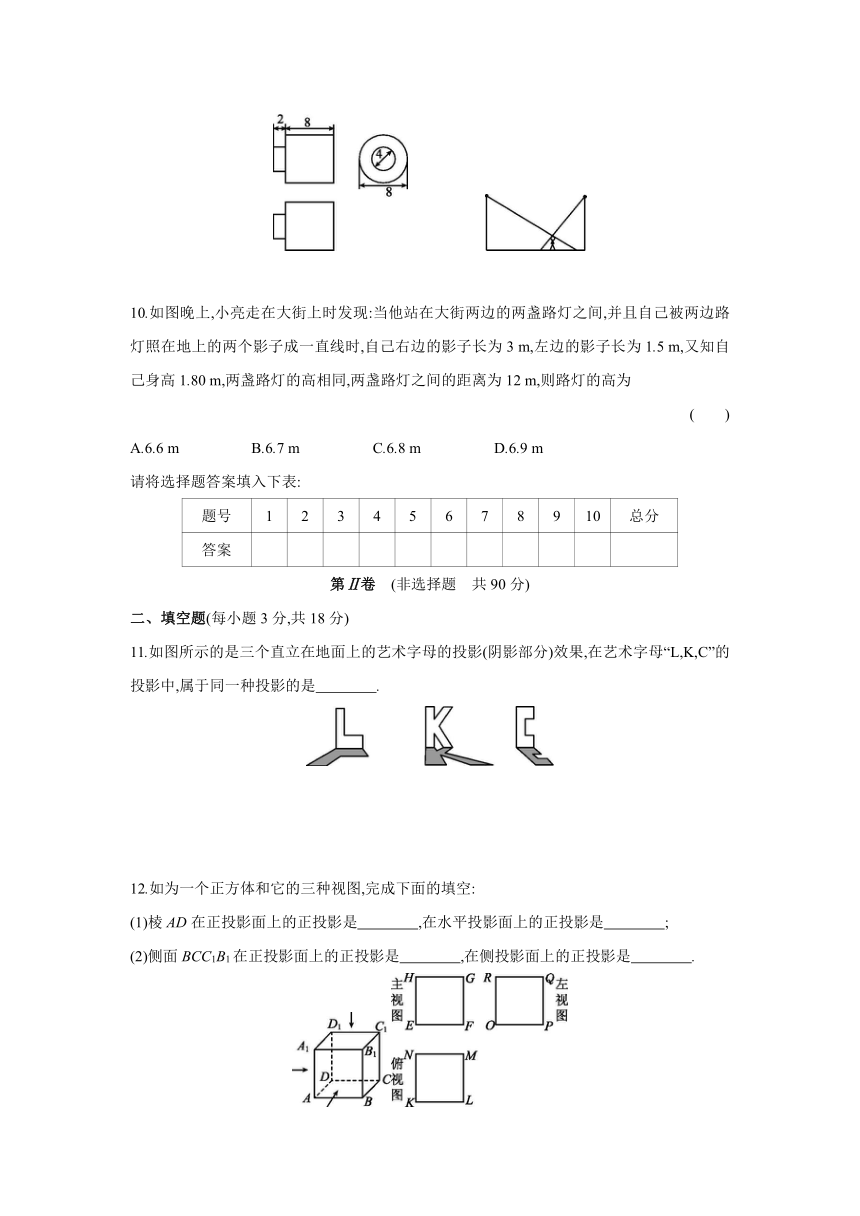
10.如图晚上,小亮走在大街上时发现:当他站在大街两边的两盏路灯之间,并且自己被两边路灯照在地上的两个影子成一直线时,自己右边的影子长为3 m,左边的影子长为1.5 m,又知自己身高1.80 m,两盏路灯的高相同,两盏路灯之间的距离为12 m,则路灯的高为
( )
A.6.6 m B.6.7 m C.6.8 m D.6.9 m
请将选择题答案填入下表:
题号 1 2 3 4 5 6 7 8 9 10 总分
答案
第Ⅱ卷 (非选择题 共90分)
二、填空题(每小题3分,共18分)
11.如图所示的是三个直立在地面上的艺术字母的投影(阴影部分)效果,在艺术字母“L,K,C”的投影中,属于同一种投影的是 .
12.如为一个正方体和它的三种视图,完成下面的填空:
(1)棱AD在正投影面上的正投影是 ,在水平投影面上的正投影是 ;
(2)侧面BCC1B1在正投影面上的正投影是 ,在侧投影面上的正投影是 .
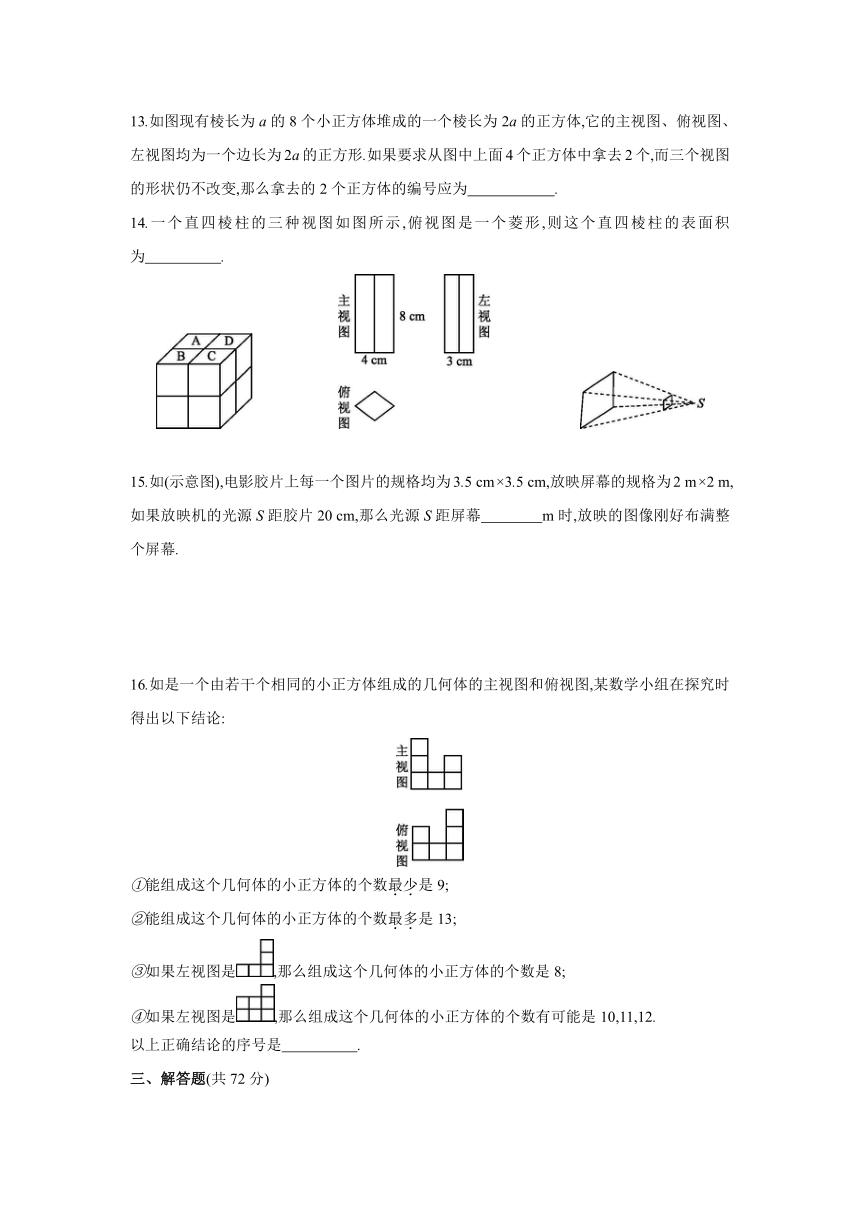
13.如图现有棱长为a的8个小正方体堆成的一个棱长为2a的正方体,它的主视图、俯视图、左视图均为一个边长为2a的正方形.如果要求从图中上面4个正方体中拿去2个,而三个视图的形状仍不改变,那么拿去的2个正方体的编号应为 .
14.一个直四棱柱的三种视图如图所示,俯视图是一个菱形,则这个直四棱柱的表面积为 .
15.如(示意图),电影胶片上每一个图片的规格均为3.5 cm×3.5 cm,放映屏幕的规格为2 m×2 m,如果放映机的光源S距胶片20 cm,那么光源S距屏幕 m时,放映的图像刚好布满整个屏幕.
16.如是一个由若干个相同的小正方体组成的几何体的主视图和俯视图,某数学小组在探究时得出以下结论:
①能组成这个几何体的小正方体的个数最少是9;
②能组成这个几何体的小正方体的个数最多是13;
③如果左视图是,那么组成这个几何体的小正方体的个数是8;
④如果左视图是,那么组成这个几何体的小正方体的个数有可能是10,11,12.
以上正确结论的序号是 .
三、解答题(共72分)
17.(6分)(1)画出如图所示物体的三种视图.
(2)一个直棱柱的主视图和俯视图如图所示,请描述这个直棱柱的形状,并补画出左视图.
18.(6分)如图某光源下有三根标杆,甲杆GH的影子为GM,乙杆EF的影子一部分落在地面上(线段EA),一部分落在斜坡AB上(线段AD).
(1)请在图中画出形成影子的光线,确定光源所在的位置R,并画出丙杆PQ在地面上的影子;
(2)在(1)的结论下,若过点F的光线FD⊥AB,斜坡与地面夹角为60°,AD=1米,AE=2米,请求出乙杆EF的高度(结果保留根号).
19.(8分)小明和小丽在操场上玩耍,小丽突然高兴地对小明说:“我踩到你的‘脑袋’了.”如表示此时小明和小丽的位置.
(1)请画出此时小丽在阳光下的影子;
(2)若已知小明身高为1.6 m,小明和小丽之间的距离为2 m,而小丽的影子长为1.75 m,求小丽的身高.
20.(8分)周末,小凯和同学带着皮尺去测量李叔叔家阳台遮阳篷的宽AB.如图由于无法直接测量,小凯便在楼前地面上选择了一条直线OP,通过在直线OP上选点观测,小凯发现当他位于点F时,他的视线从点M通过阳台点C正好落在遮阳篷点A处;当他位于点E时,视线从点N通过点C正好落在遮阳篷点B处.已知AB∥CD∥OP,点D在AG上,AD,CO,MF,NE均垂直于OP,MN=EF,露台的宽CD=GO.实际测得GO=3米,EF=3米,OE=1.5米.请根据以上信息,求出遮阳篷的宽AB.
21.(10分)如图点A,B在一条直线上,小明从点A出发沿AB方向匀速前进,4秒后走到点D,此时他(CD)在某一灯光下的影长为AD,继续沿AB方向以同样的速度匀速前进4秒后到点F,此时他(EF)的影长为2米,然后他再沿AB方向以同样的速度匀速前进2秒后到达点H,此时他(GH)处于灯光正下方(点C,E,G在一条直线上).
(1)请在图中画出光源点O的位置,并画出他位于点F时在这个灯光下的影长FM(不写画法);
(2)求小明沿AB方向匀速前进的速度.
22.(10分)已知一个几何体的三种视图如图所示.
(1)请描述这个几何体的形状;
(2)根据三种视图的尺寸,计算这个几何体的体积.
23.(12分)如图小明想测量电线杆AB的高度,发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,点A的影子为点D,量得CD=4 m,BC=10 m,坡面CD与地面成30°的角,且此时测得竖直放置的1 m长的木杆的影长为2 m,求电线杆AB的高度.
24.(12分)某兴趣小组开展课外活动.如图小明从点M出发以1.5米/秒的速度,沿射线MN方向匀速前进,2秒后到达点B,此时他(AB)在某一灯光下的影长为MB,继续按原速行走2秒到达点D,此时他(CD)在同一灯光下的影子GD仍落在其身后,并测得这个影长GD为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点F,此时A,C,E三点共线.
(1)请在图中画出光源点O的位置,并画出小明位于点F时在这个灯光下的影子FH(不写画法);
(2)求小明到达点F时的影子FH的长.
答案
第五章综合提升卷
1.D 根据题意只知道电线杆与其影子分别作为三角形的两边,可以得到两个全等三角形,平行投影和中心投影都可能出现这种情况,所以可能是平行投影也可能是中心投影.故选D.
2.C 根据平行投影的特点和规律可知,c,d是上午,a,b是下午,根据影子的长度可知先后顺序为c→d→a→b.故选C.
3.B 4.D 5.A 6.C
7.A 如图,过点E作EQ⊥FG于点Q.
∵EG=12 cm,∠EGF=30°,
∴EQ=AB=EG=6 cm.故选A.
8.A ∵AD∥BE,
∴∠CBE=∠A,∠CEB=∠D.
∴△BCE∽△ACD.
∴=,即=.
又∵BC=1 m,DE=1.8 m,CE=1.2 m,
∴=,∴AB=1.5(m).
9.B
10.A 设小亮与右边路灯的距离为x m,则与左边路灯的距离为(12-x)m,再设路灯的高为h m.
如图,∵AB⊥BC,GH⊥BC,EC⊥BC,∴AB∥GH∥EC.
易证△FHG∽△FCE,
△DHG∽△DBA.
∴=,=,
即1.8∶h=1.5∶(1.5+x),1.8∶h=3∶(3+12-x).
解得x=4,h=6.6,
即路灯的高为6.6 m.
故选A.
11.L,K 由题图可得字母L,K的投影为中心投影,字母C的投影为平行投影.
故答案为L,K.
12.(1)点E KN (2)GF 正方形PQRO
13.A,C或B,D
14.92 cm2 根据俯视图是菱形,可求得底面菱形的边长为2.5 cm,上、下底面的面积和为2××4×3=12(cm2),侧面积为2.5×8×4=80(cm2),∴直四棱柱的表面积为12+80=92(cm2).
15. 如图.由题意,得△SPE∽△SBC,
∴=.
又∵PE=3.5 cm,BC=200 cm,SR=20 cm,
∴=,
解得SD=(cm)= m.
故答案为.
16.①②④
17.解:(1)三种视图如下:
(2)这个直棱柱的形状是五棱柱,它的左视图如下:
18.解:(1)形成影子的光线和点R如图所示,QN即为丙杆PQ在地面上的影子.
(2)分别延长FD,EA交于点S,如图.
∵在Rt△ADS中,∠ADS=90°,∠DAS=60°,
∴∠S=30°.
又∵AD=1米,
∴AS=2米.
∴ES=AS+AE=2+2=4(米).
∵在Rt△EFS中,∠FES=90°,∠S=30°,
∴FS=2EF.
∴EF2+42=(2EF)2.
∴EF= (米)(负值已舍去).
故乙杆EF的高度为 米.
19.解:(1)如图所示,CA即为小丽在阳光下的影子.
(2)设小丽的身高为x m.
∵小明身高为1.6 m,小明和小丽之间的距离为2 m,小丽的影子长为1.75 m,
∴=.
解得x=1.4.即小丽的身高为1.4 m.
20. 解:如图,延长MN交OC于点H,
则HM=OF=1.5+3=4.5(米),CD=GO=3米,
MN=EF=3米.
∵CD∥HM,
∴∠ACD=∠CMH.
又∵∠ADC=∠CHM=90°,
∴△ACD∽△CMH.∴=.
∵AB∥MN,
∴∠BAC=∠NMC,∠ABC=∠MNC.
∴△ABC∽△MNC.
∴=.∴=,
即=.
∴AB=2(米).
故遮阳篷的宽AB是2米.
21.解:(1)如图所示.
(2)设小明沿AB方向匀速前进的速度为x米/秒,则AD=DF=CE=4x米,EG=FH=2x米.
∵点C,E,G在一条直线上,CG∥AB,
∴∠OCG=∠OAH,∠OEG=∠OMH.
又∠COG=∠AOH,∠EOG=∠MOH,
∴△OCG∽△OAH,△OEG∽△OMH.
∴=,=.
∴=,即=.
解得x1=0,x2=.
经检验,x1=0是原分式方程的增根,不符合题意,舍去;x2=是原分式方程的根且符合题意,故x=.
故小明沿AB方向匀速前进的速度为米/秒.
22.解:(1)该几何体是从长方体上底面正中切掉一个直三棱柱形成的几何体(底面为五边形的直棱柱).
(2)根据三种视图可知长方体体积为40×60×(80+25)=252000(mm3),
切掉的直三棱柱体积为×80×(40-20)×60=48000(mm3),
则该几何体的体积为252000-48000=204000(mm3).
即这个几何体的体积为204000 mm3.
23.解:延长AD交BC的延长线于点E,过点D作DF⊥CE,垂足为F.
∵∠DCF=30°,CD=4 m,
∴DF=2 m,CF=2 m.
又∵竖直放置的1 m长的木杆的影长为2 m,
∴=,即=.
∴EF=4(m).
∴大树AB在水平地面上的影长=BC+CF+EF=10+2+4=(14+2)m.
∴=.
解得AB=(7+)m.
故电线杆AB的高度是(7+)m.
24.解:(1)如图,点O和FH即为所作.
(2)依题意知BM=BD=2×1.5=3(米),GD=1.2米,DF=1.5×1.5×2=4.5(米).
设AB=CD=EF=a米.
如图,过点O作OK⊥MN于点K,
∴AB∥CD∥EF∥OK.
∵AB∥OK,
∴∠MAB=∠MOK.
又∵∠M=∠M,
∴△MAB∽△MOK.
∴=,即=.①
∵CD∥OK,∠GCD=∠GOK.
又∵∠CGD=∠OGK,
∴△GCD∽△GOK.
∴=,即=.②
由①②得=,解得DK=2(米).
∴==,FK=DF-DK=4.5-2=2.5(米).
∵EF∥OK,
∴∠HEF=∠HOK.
又∵∠EHF=∠OHK,
∴△HEF∽△HOK.
∴=,即=.
∴=.∴FH=1.5(米).
故小明到达点F时的影子FH的长为1.5米.
第Ⅰ卷 (选择题 共30分)
一、选择题(每小题3分,共30分)
1.有两根电线杆在地面上形成了各自的影子,若以电线杆与其影子分别作为三角形的两边,可以得到两个全等三角形,则这种投影现象为 ( )
A.平行投影
B.中心投影
C.既不是平行投影也不是中心投影
D.可能是平行投影也可能是中心投影
2. 如图所示四幅图是两个物体不同时刻在太阳光下的影子,按照时间先后顺序排列正确的是 ( )
A.a→b→c→d B.d→b→c→a
C.c→d→a→b D.a→c→b→d
3.如是由5块完全相同的小正方体所搭成的几何体的俯视图,小正方形中的数字表示在该位置处小正方体的个数,则该几何体的主视图是 ( )
4.如图所示的支架(一种小零件)的两个台阶的高度和宽度相等,则它的左视图为
( )
5.如是一个几何体的三种视图,则该几何体的展开图可以是 ( )
6.一个几何体的三种视图如图所示,则这个几何体是 ( )
7.如中的三棱柱的三种视图如图所示,在△EFG中,EG=12 cm,∠EGF=30°,则AB的长为 ( )
A.6 cm B.3 cm C.3 cm D.6 cm
8.如图阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8 m,窗户下檐到地面的距离BC=1 m,CE=1.2 m,那么窗户的高AB为 ( )
A.1.5 m B.1.6 m C.1.86 m D.2.16 m
9.如是某几何体的三种视图,根据图中所标的数据求得该几何体的体积为 ( )
A.236π B.136π C.132π D.120π
10.如图晚上,小亮走在大街上时发现:当他站在大街两边的两盏路灯之间,并且自己被两边路灯照在地上的两个影子成一直线时,自己右边的影子长为3 m,左边的影子长为1.5 m,又知自己身高1.80 m,两盏路灯的高相同,两盏路灯之间的距离为12 m,则路灯的高为
( )
A.6.6 m B.6.7 m C.6.8 m D.6.9 m
请将选择题答案填入下表:
题号 1 2 3 4 5 6 7 8 9 10 总分
答案
第Ⅱ卷 (非选择题 共90分)
二、填空题(每小题3分,共18分)
11.如图所示的是三个直立在地面上的艺术字母的投影(阴影部分)效果,在艺术字母“L,K,C”的投影中,属于同一种投影的是 .
12.如为一个正方体和它的三种视图,完成下面的填空:
(1)棱AD在正投影面上的正投影是 ,在水平投影面上的正投影是 ;
(2)侧面BCC1B1在正投影面上的正投影是 ,在侧投影面上的正投影是 .
13.如图现有棱长为a的8个小正方体堆成的一个棱长为2a的正方体,它的主视图、俯视图、左视图均为一个边长为2a的正方形.如果要求从图中上面4个正方体中拿去2个,而三个视图的形状仍不改变,那么拿去的2个正方体的编号应为 .
14.一个直四棱柱的三种视图如图所示,俯视图是一个菱形,则这个直四棱柱的表面积为 .
15.如(示意图),电影胶片上每一个图片的规格均为3.5 cm×3.5 cm,放映屏幕的规格为2 m×2 m,如果放映机的光源S距胶片20 cm,那么光源S距屏幕 m时,放映的图像刚好布满整个屏幕.
16.如是一个由若干个相同的小正方体组成的几何体的主视图和俯视图,某数学小组在探究时得出以下结论:
①能组成这个几何体的小正方体的个数最少是9;
②能组成这个几何体的小正方体的个数最多是13;
③如果左视图是,那么组成这个几何体的小正方体的个数是8;
④如果左视图是,那么组成这个几何体的小正方体的个数有可能是10,11,12.
以上正确结论的序号是 .
三、解答题(共72分)
17.(6分)(1)画出如图所示物体的三种视图.
(2)一个直棱柱的主视图和俯视图如图所示,请描述这个直棱柱的形状,并补画出左视图.
18.(6分)如图某光源下有三根标杆,甲杆GH的影子为GM,乙杆EF的影子一部分落在地面上(线段EA),一部分落在斜坡AB上(线段AD).
(1)请在图中画出形成影子的光线,确定光源所在的位置R,并画出丙杆PQ在地面上的影子;
(2)在(1)的结论下,若过点F的光线FD⊥AB,斜坡与地面夹角为60°,AD=1米,AE=2米,请求出乙杆EF的高度(结果保留根号).
19.(8分)小明和小丽在操场上玩耍,小丽突然高兴地对小明说:“我踩到你的‘脑袋’了.”如表示此时小明和小丽的位置.
(1)请画出此时小丽在阳光下的影子;
(2)若已知小明身高为1.6 m,小明和小丽之间的距离为2 m,而小丽的影子长为1.75 m,求小丽的身高.
20.(8分)周末,小凯和同学带着皮尺去测量李叔叔家阳台遮阳篷的宽AB.如图由于无法直接测量,小凯便在楼前地面上选择了一条直线OP,通过在直线OP上选点观测,小凯发现当他位于点F时,他的视线从点M通过阳台点C正好落在遮阳篷点A处;当他位于点E时,视线从点N通过点C正好落在遮阳篷点B处.已知AB∥CD∥OP,点D在AG上,AD,CO,MF,NE均垂直于OP,MN=EF,露台的宽CD=GO.实际测得GO=3米,EF=3米,OE=1.5米.请根据以上信息,求出遮阳篷的宽AB.
21.(10分)如图点A,B在一条直线上,小明从点A出发沿AB方向匀速前进,4秒后走到点D,此时他(CD)在某一灯光下的影长为AD,继续沿AB方向以同样的速度匀速前进4秒后到点F,此时他(EF)的影长为2米,然后他再沿AB方向以同样的速度匀速前进2秒后到达点H,此时他(GH)处于灯光正下方(点C,E,G在一条直线上).
(1)请在图中画出光源点O的位置,并画出他位于点F时在这个灯光下的影长FM(不写画法);
(2)求小明沿AB方向匀速前进的速度.
22.(10分)已知一个几何体的三种视图如图所示.
(1)请描述这个几何体的形状;
(2)根据三种视图的尺寸,计算这个几何体的体积.
23.(12分)如图小明想测量电线杆AB的高度,发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,点A的影子为点D,量得CD=4 m,BC=10 m,坡面CD与地面成30°的角,且此时测得竖直放置的1 m长的木杆的影长为2 m,求电线杆AB的高度.
24.(12分)某兴趣小组开展课外活动.如图小明从点M出发以1.5米/秒的速度,沿射线MN方向匀速前进,2秒后到达点B,此时他(AB)在某一灯光下的影长为MB,继续按原速行走2秒到达点D,此时他(CD)在同一灯光下的影子GD仍落在其身后,并测得这个影长GD为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点F,此时A,C,E三点共线.
(1)请在图中画出光源点O的位置,并画出小明位于点F时在这个灯光下的影子FH(不写画法);
(2)求小明到达点F时的影子FH的长.
答案
第五章综合提升卷
1.D 根据题意只知道电线杆与其影子分别作为三角形的两边,可以得到两个全等三角形,平行投影和中心投影都可能出现这种情况,所以可能是平行投影也可能是中心投影.故选D.
2.C 根据平行投影的特点和规律可知,c,d是上午,a,b是下午,根据影子的长度可知先后顺序为c→d→a→b.故选C.
3.B 4.D 5.A 6.C
7.A 如图,过点E作EQ⊥FG于点Q.
∵EG=12 cm,∠EGF=30°,
∴EQ=AB=EG=6 cm.故选A.
8.A ∵AD∥BE,
∴∠CBE=∠A,∠CEB=∠D.
∴△BCE∽△ACD.
∴=,即=.
又∵BC=1 m,DE=1.8 m,CE=1.2 m,
∴=,∴AB=1.5(m).
9.B
10.A 设小亮与右边路灯的距离为x m,则与左边路灯的距离为(12-x)m,再设路灯的高为h m.
如图,∵AB⊥BC,GH⊥BC,EC⊥BC,∴AB∥GH∥EC.
易证△FHG∽△FCE,
△DHG∽△DBA.
∴=,=,
即1.8∶h=1.5∶(1.5+x),1.8∶h=3∶(3+12-x).
解得x=4,h=6.6,
即路灯的高为6.6 m.
故选A.
11.L,K 由题图可得字母L,K的投影为中心投影,字母C的投影为平行投影.
故答案为L,K.
12.(1)点E KN (2)GF 正方形PQRO
13.A,C或B,D
14.92 cm2 根据俯视图是菱形,可求得底面菱形的边长为2.5 cm,上、下底面的面积和为2××4×3=12(cm2),侧面积为2.5×8×4=80(cm2),∴直四棱柱的表面积为12+80=92(cm2).
15. 如图.由题意,得△SPE∽△SBC,
∴=.
又∵PE=3.5 cm,BC=200 cm,SR=20 cm,
∴=,
解得SD=(cm)= m.
故答案为.
16.①②④
17.解:(1)三种视图如下:
(2)这个直棱柱的形状是五棱柱,它的左视图如下:
18.解:(1)形成影子的光线和点R如图所示,QN即为丙杆PQ在地面上的影子.
(2)分别延长FD,EA交于点S,如图.
∵在Rt△ADS中,∠ADS=90°,∠DAS=60°,
∴∠S=30°.
又∵AD=1米,
∴AS=2米.
∴ES=AS+AE=2+2=4(米).
∵在Rt△EFS中,∠FES=90°,∠S=30°,
∴FS=2EF.
∴EF2+42=(2EF)2.
∴EF= (米)(负值已舍去).
故乙杆EF的高度为 米.
19.解:(1)如图所示,CA即为小丽在阳光下的影子.
(2)设小丽的身高为x m.
∵小明身高为1.6 m,小明和小丽之间的距离为2 m,小丽的影子长为1.75 m,
∴=.
解得x=1.4.即小丽的身高为1.4 m.
20. 解:如图,延长MN交OC于点H,
则HM=OF=1.5+3=4.5(米),CD=GO=3米,
MN=EF=3米.
∵CD∥HM,
∴∠ACD=∠CMH.
又∵∠ADC=∠CHM=90°,
∴△ACD∽△CMH.∴=.
∵AB∥MN,
∴∠BAC=∠NMC,∠ABC=∠MNC.
∴△ABC∽△MNC.
∴=.∴=,
即=.
∴AB=2(米).
故遮阳篷的宽AB是2米.
21.解:(1)如图所示.
(2)设小明沿AB方向匀速前进的速度为x米/秒,则AD=DF=CE=4x米,EG=FH=2x米.
∵点C,E,G在一条直线上,CG∥AB,
∴∠OCG=∠OAH,∠OEG=∠OMH.
又∠COG=∠AOH,∠EOG=∠MOH,
∴△OCG∽△OAH,△OEG∽△OMH.
∴=,=.
∴=,即=.
解得x1=0,x2=.
经检验,x1=0是原分式方程的增根,不符合题意,舍去;x2=是原分式方程的根且符合题意,故x=.
故小明沿AB方向匀速前进的速度为米/秒.
22.解:(1)该几何体是从长方体上底面正中切掉一个直三棱柱形成的几何体(底面为五边形的直棱柱).
(2)根据三种视图可知长方体体积为40×60×(80+25)=252000(mm3),
切掉的直三棱柱体积为×80×(40-20)×60=48000(mm3),
则该几何体的体积为252000-48000=204000(mm3).
即这个几何体的体积为204000 mm3.
23.解:延长AD交BC的延长线于点E,过点D作DF⊥CE,垂足为F.
∵∠DCF=30°,CD=4 m,
∴DF=2 m,CF=2 m.
又∵竖直放置的1 m长的木杆的影长为2 m,
∴=,即=.
∴EF=4(m).
∴大树AB在水平地面上的影长=BC+CF+EF=10+2+4=(14+2)m.
∴=.
解得AB=(7+)m.
故电线杆AB的高度是(7+)m.
24.解:(1)如图,点O和FH即为所作.
(2)依题意知BM=BD=2×1.5=3(米),GD=1.2米,DF=1.5×1.5×2=4.5(米).
设AB=CD=EF=a米.
如图,过点O作OK⊥MN于点K,
∴AB∥CD∥EF∥OK.
∵AB∥OK,
∴∠MAB=∠MOK.
又∵∠M=∠M,
∴△MAB∽△MOK.
∴=,即=.①
∵CD∥OK,∠GCD=∠GOK.
又∵∠CGD=∠OGK,
∴△GCD∽△GOK.
∴=,即=.②
由①②得=,解得DK=2(米).
∴==,FK=DF-DK=4.5-2=2.5(米).
∵EF∥OK,
∴∠HEF=∠HOK.
又∵∠EHF=∠OHK,
∴△HEF∽△HOK.
∴=,即=.
∴=.∴FH=1.5(米).
故小明到达点F时的影子FH的长为1.5米.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
