北师大版(新)八上-2.2 平方根 第一课时【优质课件】
文档属性
| 名称 | 北师大版(新)八上-2.2 平方根 第一课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览










文档简介
(共35张PPT)
2.2 平方根
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
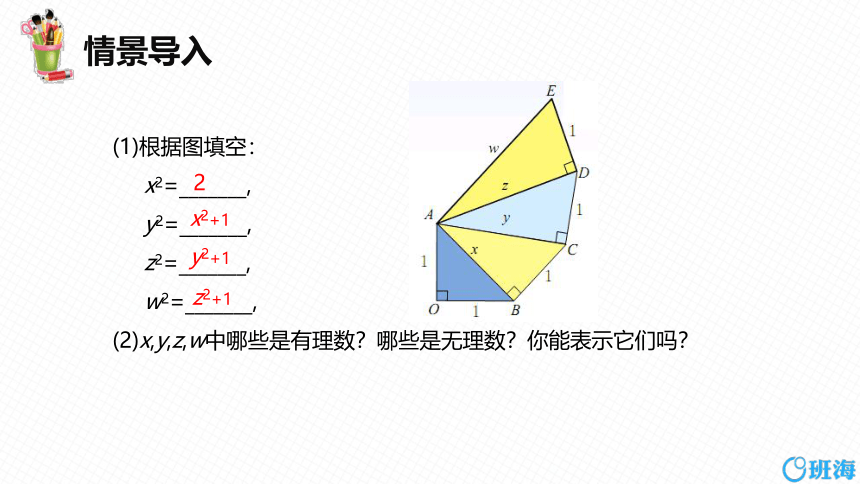
(1)根据图填空:
x2=_______,
y2=_______,
z2=_______,
w2=_______,
(2)x,y,z,w中哪些是有理数?哪些是无理数?你能表示它们吗?
2
x2+1
y2+1
z2+1
新课精讲
探索新知
1
知识点
算术平方根的定义
定义:一般地,如果一个正数x的平方等于a, 即x2=a,那么这个正数x就叫做a的算术平根.
规定:0的算术平方根是0.
表示方法:正数a的算术平方根表示为 读作 “根号a”.
探索新知
例1 下列说法中,正确的是( )
A.3是9的算术平方根
B.-2是4的算术平方根
C. (-2)2的算术平方根是-2
D.-9的算术平方根是3
A
探索新知
要正确把握算术平方根的定义.因为3的平方等于9,所以3是9的算术平方根;因为-2不是正数,所以-2不是4的算术平方根;因为(-2)2=4,而22=4,所以2是(-2)2的算术平方根;负数没有算术平方根.
导引:
探索新知
总 结
算术平方根具有双重非负性,这个数是非负数,它的算术平方根也是非负数.
典题精讲
1 数5的算术平方根为( )
A. B.25 C.±25 D.±
2 下列说法正确的是( )
A.因为62=36,所以6是36的算术平方根
B.因为(-6)2=36,所以-6是36的算术平方根
C.因为(±6)2=36,所以6和-6都是36的算术平方根
D.以上说法都不对
A
A
探索新知
2
知识点
求算术平方根
例2 求下列各数的算术平方根:
(1)900; (2)1; (3) ; (4) 14.
解:(1)因为302 = 900,所以900的算术平方根是30,即
(2)因为12=1,所以1的算术平方根是1,即
(3)因为 所以 的算术平方根是
(4)14的算术平方根是
探索新知
例3 求下列各数的算术平方根:
(1)64; (2)
(3)0.36; (4)
导引:根据算术平方根的定义求一个非负数的算术平方根,只要找到一个非负数的平方等于这个非负数即可.
探索新知
解:(1)因为82=64 ,所以 64的算术平方根是8,即
(2)因为 所以 的算术平方根是 ,
(3)因为0.62=0.36,所以0.36的算术平方根是0.6,即
(4)因为 92=81,所以 =9.而32= 9,所以 的算术平方根是3.
探索新知
总 结
(1)求一个数的算术平方根时,首先要弄清是求哪个数的算术平方根,分清求 的算术平方根与81的算术平方根的不同意义,不要被表面现象迷惑.
(2)求一个非负数的算术平方根常借助于平方运算,因此熟记常用平方数对求一个数的算术平方根十分有用.
注意:求 的值实质就是求81的算术平方根,求 的算术平方根实质是求9的算术平方根.
典题精讲
的算术平方根的相反数和倒数分别是 ________.
2 的算术平方根是( )
A.2 B.±2
C. D.±
C
探索新知
3
知识点
算术平方根的非负性
1.要点精析:
(1)算术平方根 具有双重非负性:
①a是非负数,即a≥0;
②算术平方根 是非负数,即 ≥0.
(2)算术平方根是它本身的数只有0和1.
2.性质:
(1)正数的算术平方根是一个正数; (2)0的算术平方根是0;
(3)负数没有算术平方根;(4)a(a≥0)越大,它的算术平方根也越大.
探索新知
例4 (1)已知y= + +5,求2x+y的算术平方根.
导引:由于只有非负数才有算术平方根,因此本题中x-2≥0,且2-x≥0.求得x的值后从而可得y的值,进而问题得解.
解:由 中a≥0知,等式成立的条件是x-2≥0且
2-x≥0.所以x≥2且x≤2.
所以x=2.所以y=5.
所以2x+y=2×2+5=9.
因为9的算术平方根是3,所以2x+y的算术平
方根是3,即
探索新知
总 结
要使y= + +5有意义,需满足x-2≥0,2-x≥0.只有它们都等于0,这两个式子才都有意义.
探索新知
(2)已知x,y为有理数,且 +3(y-2)2=0,求x-y的值.
导引:算术平方根和平方都具有非负性,即 ≥0, a2≥0.由几个非负数相加和为0,可得每一个非负数都为0,由此可求出x和y的值,进而求得答案.
解:由题意可得x-1=0,y-2=0.
所以x=1,y=2.
所以x-y=1-2=-1.
探索新知
总 结
(1)算术平方根和数的平方、绝对值一样,都是非负数,即 ≥0,a2≥0,|a|≥0;当几个非负数的和为0时,则其中每一个非负数都为0.
(2)只有非负数才有算术平方根,因此当同时出现 时,a只有为0才有意义.
典题精讲
1 (1) 中,被开方数a是________,即a___0;
(2) 是________,即 _____0,即非负数的算术平方根是_________;负数没有算术平方根,即当a_____0时, 无意义.
非负数
≥
非负数
≥
非负数
<
若 +|2a-b+1|=0,则(b-a)2 015=( )
A.-1 B.1
C.52 015 D.-52 015
A
学以致用
小试牛刀
1.一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x叫做a的________________.a的算术平方根记为________,读作“____________”,a叫做__________.规定:0的算术平方根是________.
算术平方根
根号a
被开方数
0
2.求一个数的算术平方根与求一个非负数的平方恰好是互逆的两种运算,因而,求一个数的算术平方根实际上可以转化为求一个非负数的______运算.但是,只有________有算术平方根,______没有算术平方根.算术平方根等于它本身的数有_______.
平方
正数和0
负数
0和1
小试牛刀
3.a的算术平方根 具有双重非负性:
(1)_______________________________,即a≥0;
(2)一个非负数的算术平方根也是非负数,即______≥0.
形如a,︱a︱,a2的式子是数学中常见的三种非负数的表现形式.
被开方数一定是非负数
4.已知有理数m,n满足|n-2|+ =0,则m+2n的值为________.
3
小试牛刀
5.下列说法:
①-1的算术平方根是1;②-1的平方是±1;③ 1的算术平方根是1;④ 0的算术平方根是0.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
B
6.下列说法正确的是( )
A . 表示25的算术平方根
B.- 表示2的算术平方根
C.2的算术平方根记作±
D.2是 的算术平方根
A
小试牛刀
7.计算 的结果为( )
A.6 B.-6 C.18 D.-18
8.下列说法正确的是( )
A.因为62=36,所以6是36的算术平方根
B.因为(-6)2=36,所以-6是36的算术平方根
C.因为(±6)2=36,所以6和-6都是36的算术平方根
D.以上说法都不对
A
A
小试牛刀
9.下列运算正确的是( )
A. =-3 B.|3|=-3
C. =±3 D.|-3|=3
10.已知一个表面积为12 dm2的正方体,则这个正方体的棱长为( )
A.1 dm B. dm C. dm D.3 dm
D
B
小试牛刀
11.要使 有意义,则x的取值范围是( )
A.x<1 B.x≥1
C.x≤-1 D.x<-1
B
12.下列说法正确的有( )
①任何数都有算术平方根;②一个数的算术平方根一定是正数;③a2的算术平方根是a;④(π-4)2的算术平方根是π-4;⑤算术平方根不可能是负数.
A.1个 B.2个 C.3个 D.4个
A
小试牛刀
13.求下列各数的算术平方根:
(1)625; (2)(-3)2; (3) ;
解:(1)因为252=625,
所以625的算术平方根是25,即 =25;
(2)(-3)2=9,因为32=9,所以9的算术平方根是3,
即 =3;
(3) =4,因为22=4,
所以4的算术平方根是2,
即 =2;
小试牛刀
(4) ; (5)0.49; (6)0.
(4)因为 = ,所以 的算术平方根是 ,
即 = ;
(5)因为0.72=0.49,
所以0.49的算术平方根是0.7,即 =0.7;
(6)0的算术平方根是0,即 =0.
小试牛刀
14.已知a-2的算术平方根是0,3a+b-1的算术平方根是5,求b-a2的算术平方根.
解:由题意,得a-2=0,3a+b-1=25,
解得a=2,b=20.
所以 = =4.
小试牛刀
15.已知a,b为有理数,且 +2 =b+4,求a,b的值.
解:由算术平方根中被开方数的非负性易得a=5,
所以b+4=0.
故b=-4.
课堂小结
课堂小结
1. 表示的是a的算术平方根,由算术平方根的定义知它具有“双重”非负性:a≥0, ≥0,即算术平方根及它的被开方数都为非负数.
2.对于所有的算术平方根,被开方数越大,对应的算术平方根也越大;反之亦然.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
2.2 平方根
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
(1)根据图填空:
x2=_______,
y2=_______,
z2=_______,
w2=_______,
(2)x,y,z,w中哪些是有理数?哪些是无理数?你能表示它们吗?
2
x2+1
y2+1
z2+1
新课精讲
探索新知
1
知识点
算术平方根的定义
定义:一般地,如果一个正数x的平方等于a, 即x2=a,那么这个正数x就叫做a的算术平根.
规定:0的算术平方根是0.
表示方法:正数a的算术平方根表示为 读作 “根号a”.
探索新知
例1 下列说法中,正确的是( )
A.3是9的算术平方根
B.-2是4的算术平方根
C. (-2)2的算术平方根是-2
D.-9的算术平方根是3
A
探索新知
要正确把握算术平方根的定义.因为3的平方等于9,所以3是9的算术平方根;因为-2不是正数,所以-2不是4的算术平方根;因为(-2)2=4,而22=4,所以2是(-2)2的算术平方根;负数没有算术平方根.
导引:
探索新知
总 结
算术平方根具有双重非负性,这个数是非负数,它的算术平方根也是非负数.
典题精讲
1 数5的算术平方根为( )
A. B.25 C.±25 D.±
2 下列说法正确的是( )
A.因为62=36,所以6是36的算术平方根
B.因为(-6)2=36,所以-6是36的算术平方根
C.因为(±6)2=36,所以6和-6都是36的算术平方根
D.以上说法都不对
A
A
探索新知
2
知识点
求算术平方根
例2 求下列各数的算术平方根:
(1)900; (2)1; (3) ; (4) 14.
解:(1)因为302 = 900,所以900的算术平方根是30,即
(2)因为12=1,所以1的算术平方根是1,即
(3)因为 所以 的算术平方根是
(4)14的算术平方根是
探索新知
例3 求下列各数的算术平方根:
(1)64; (2)
(3)0.36; (4)
导引:根据算术平方根的定义求一个非负数的算术平方根,只要找到一个非负数的平方等于这个非负数即可.
探索新知
解:(1)因为82=64 ,所以 64的算术平方根是8,即
(2)因为 所以 的算术平方根是 ,
(3)因为0.62=0.36,所以0.36的算术平方根是0.6,即
(4)因为 92=81,所以 =9.而32= 9,所以 的算术平方根是3.
探索新知
总 结
(1)求一个数的算术平方根时,首先要弄清是求哪个数的算术平方根,分清求 的算术平方根与81的算术平方根的不同意义,不要被表面现象迷惑.
(2)求一个非负数的算术平方根常借助于平方运算,因此熟记常用平方数对求一个数的算术平方根十分有用.
注意:求 的值实质就是求81的算术平方根,求 的算术平方根实质是求9的算术平方根.
典题精讲
的算术平方根的相反数和倒数分别是 ________.
2 的算术平方根是( )
A.2 B.±2
C. D.±
C
探索新知
3
知识点
算术平方根的非负性
1.要点精析:
(1)算术平方根 具有双重非负性:
①a是非负数,即a≥0;
②算术平方根 是非负数,即 ≥0.
(2)算术平方根是它本身的数只有0和1.
2.性质:
(1)正数的算术平方根是一个正数; (2)0的算术平方根是0;
(3)负数没有算术平方根;(4)a(a≥0)越大,它的算术平方根也越大.
探索新知
例4 (1)已知y= + +5,求2x+y的算术平方根.
导引:由于只有非负数才有算术平方根,因此本题中x-2≥0,且2-x≥0.求得x的值后从而可得y的值,进而问题得解.
解:由 中a≥0知,等式成立的条件是x-2≥0且
2-x≥0.所以x≥2且x≤2.
所以x=2.所以y=5.
所以2x+y=2×2+5=9.
因为9的算术平方根是3,所以2x+y的算术平
方根是3,即
探索新知
总 结
要使y= + +5有意义,需满足x-2≥0,2-x≥0.只有它们都等于0,这两个式子才都有意义.
探索新知
(2)已知x,y为有理数,且 +3(y-2)2=0,求x-y的值.
导引:算术平方根和平方都具有非负性,即 ≥0, a2≥0.由几个非负数相加和为0,可得每一个非负数都为0,由此可求出x和y的值,进而求得答案.
解:由题意可得x-1=0,y-2=0.
所以x=1,y=2.
所以x-y=1-2=-1.
探索新知
总 结
(1)算术平方根和数的平方、绝对值一样,都是非负数,即 ≥0,a2≥0,|a|≥0;当几个非负数的和为0时,则其中每一个非负数都为0.
(2)只有非负数才有算术平方根,因此当同时出现 时,a只有为0才有意义.
典题精讲
1 (1) 中,被开方数a是________,即a___0;
(2) 是________,即 _____0,即非负数的算术平方根是_________;负数没有算术平方根,即当a_____0时, 无意义.
非负数
≥
非负数
≥
非负数
<
若 +|2a-b+1|=0,则(b-a)2 015=( )
A.-1 B.1
C.52 015 D.-52 015
A
学以致用
小试牛刀
1.一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x叫做a的________________.a的算术平方根记为________,读作“____________”,a叫做__________.规定:0的算术平方根是________.
算术平方根
根号a
被开方数
0
2.求一个数的算术平方根与求一个非负数的平方恰好是互逆的两种运算,因而,求一个数的算术平方根实际上可以转化为求一个非负数的______运算.但是,只有________有算术平方根,______没有算术平方根.算术平方根等于它本身的数有_______.
平方
正数和0
负数
0和1
小试牛刀
3.a的算术平方根 具有双重非负性:
(1)_______________________________,即a≥0;
(2)一个非负数的算术平方根也是非负数,即______≥0.
形如a,︱a︱,a2的式子是数学中常见的三种非负数的表现形式.
被开方数一定是非负数
4.已知有理数m,n满足|n-2|+ =0,则m+2n的值为________.
3
小试牛刀
5.下列说法:
①-1的算术平方根是1;②-1的平方是±1;③ 1的算术平方根是1;④ 0的算术平方根是0.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
B
6.下列说法正确的是( )
A . 表示25的算术平方根
B.- 表示2的算术平方根
C.2的算术平方根记作±
D.2是 的算术平方根
A
小试牛刀
7.计算 的结果为( )
A.6 B.-6 C.18 D.-18
8.下列说法正确的是( )
A.因为62=36,所以6是36的算术平方根
B.因为(-6)2=36,所以-6是36的算术平方根
C.因为(±6)2=36,所以6和-6都是36的算术平方根
D.以上说法都不对
A
A
小试牛刀
9.下列运算正确的是( )
A. =-3 B.|3|=-3
C. =±3 D.|-3|=3
10.已知一个表面积为12 dm2的正方体,则这个正方体的棱长为( )
A.1 dm B. dm C. dm D.3 dm
D
B
小试牛刀
11.要使 有意义,则x的取值范围是( )
A.x<1 B.x≥1
C.x≤-1 D.x<-1
B
12.下列说法正确的有( )
①任何数都有算术平方根;②一个数的算术平方根一定是正数;③a2的算术平方根是a;④(π-4)2的算术平方根是π-4;⑤算术平方根不可能是负数.
A.1个 B.2个 C.3个 D.4个
A
小试牛刀
13.求下列各数的算术平方根:
(1)625; (2)(-3)2; (3) ;
解:(1)因为252=625,
所以625的算术平方根是25,即 =25;
(2)(-3)2=9,因为32=9,所以9的算术平方根是3,
即 =3;
(3) =4,因为22=4,
所以4的算术平方根是2,
即 =2;
小试牛刀
(4) ; (5)0.49; (6)0.
(4)因为 = ,所以 的算术平方根是 ,
即 = ;
(5)因为0.72=0.49,
所以0.49的算术平方根是0.7,即 =0.7;
(6)0的算术平方根是0,即 =0.
小试牛刀
14.已知a-2的算术平方根是0,3a+b-1的算术平方根是5,求b-a2的算术平方根.
解:由题意,得a-2=0,3a+b-1=25,
解得a=2,b=20.
所以 = =4.
小试牛刀
15.已知a,b为有理数,且 +2 =b+4,求a,b的值.
解:由算术平方根中被开方数的非负性易得a=5,
所以b+4=0.
故b=-4.
课堂小结
课堂小结
1. 表示的是a的算术平方根,由算术平方根的定义知它具有“双重”非负性:a≥0, ≥0,即算术平方根及它的被开方数都为非负数.
2.对于所有的算术平方根,被开方数越大,对应的算术平方根也越大;反之亦然.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
