北师大版数学九年级上册同步提优训练:4.3相似多边形(word版含答案)
文档属性
| 名称 | 北师大版数学九年级上册同步提优训练:4.3相似多边形(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 234.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-11 00:00:00 | ||
图片预览



文档简介
3 相似多边形
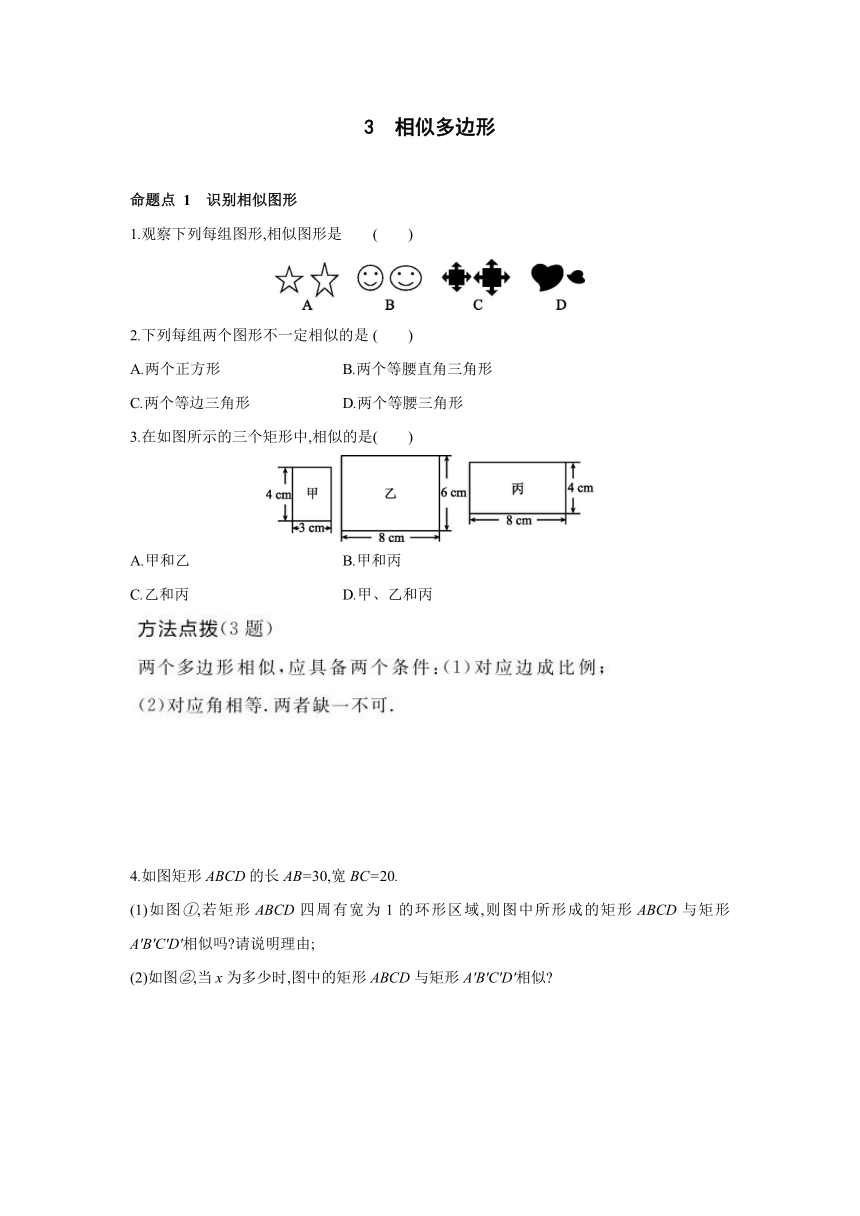
命题点 1 识别相似图形
1.观察下列每组图形,相似图形是 ( )
2.下列每组两个图形不一定相似的是 ( )
A.两个正方形 B.两个等腰直角三角形
C.两个等边三角形 D.两个等腰三角形
3.在如图所示的三个矩形中,相似的是( )
A.甲和乙 B.甲和丙
C.乙和丙 D.甲、乙和丙
4.如图矩形ABCD的长AB=30,宽BC=20.
(1)如图①,若矩形ABCD四周有宽为1的环形区域,则图中所形成的矩形ABCD与矩形A'B'C'D'相似吗 请说明理由;
(2)如图②,当x为多少时,图中的矩形ABCD与矩形A'B'C'D'相似
命题点 2 利用相似多边形的定义求值
5.用同一张图片打印出来的两张照片,一张为2寸,另一张为6寸,则这两张照片上的像的相似比是 .
6.如图在正方形ABCD中,E是对角线BD上的一点,BE=BC,过点E作EF⊥AB,EG⊥BC,垂足分别为F,G,则正方形FBGE与正方形ABCD的相似比为 .
7.如图四边形ABCD为平行四边形,AE平分∠BAD交BC于点E,过点E作EF∥AB,交AD于点F,连接BF.
(1)求证:BF平分∠ABC;
(2)若AB=6,且四边形ABCD∽四边形CEFD,求BC的长.
8.如图E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且菱形AEFG∽菱形ABCD,连接EB,GD.
(1)求证:EB=GD;
(2)若∠DAB=60°,AB=2,AG=,求GD的长.
命题点 3 利用定义判定多边形相似
9.如图四边形ABCD的对角线相交于点O,A',B',C',D'分别是OA,OB,OC,OD的中点.
求证:四边形ABCD∽四边形A'B'C'D'.
10.彼此相似的正方形A1B1C1O,A2B2C2C1,A3B3C3C2如图所示,点A1,A2,A3和点C1,C2,C3分别在直线y=kx+b(k>0)和x轴上,点B3的坐标是,,则5k-bk的值为 .
11.如.
(1)已知矩形纸片A,它的长和宽的比是,将矩形A对折,得矩形A1,再将矩形A1对折,得矩形A2,依次对折下去得矩形A3,A4,…,An,那么矩形A,A1,A2,A3,A4,…,An都相似吗
(2)如果矩形A的长和宽的比为(q答案
3 相似多边形
1.C 2.D 3.A
4.解:(1)不相似.
理由:∵AB=30,A'B'=28,BC=20,B'C'=18,
而≠,∴两个矩形不相似.
(2)若矩形ABCD与矩形A'B'C'D'相似,有以下两种情况:
①=,即=,
解得x=1.5;
②=,即=,解得x=9.
∴当x为1.5或9时,矩形ABCD与矩形A'B'C'D'相似.
5.1∶3
6. 设BG=x,
则BE=x.
∵BE=BC,
∴BC=x.
则正方形FBGE与正方形ABCD的相似比=BG∶BC=x∶x=∶2.
7.解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠FAE=∠AEB.
∵AE平分∠BAD,∴∠FAE=∠BAE.
∴∠BAE=∠AEB.∴AB=EB.
∵AD∥BC,EF∥AB,
∴四边形ABEF是平行四边形.
又∵AB=EB,∴四边形ABEF是菱形.
∴BF平分∠ABC.
(2)∵EF∥AB,AB∥CD,∴EF∥CD.
又∵AD∥BC,∴四边形CEFD是平行四边形.
由(1)知四边形ABEF是菱形,∴EF=BE=AB=6.
∵四边形ABCD∽四边形CEFD,
∴=,即=,
解得BC=3+3(负值已舍去).
8.解:(1)证明:∵菱形AEFG∽菱形ABCD,
∴AB=AD,AE=AG,∠EAG=∠BAD.
∴∠EAB=∠GAD.
∴△EAB≌△GAD.则EB=GD.
(2)过点B作BO⊥AC于点O.
∵在菱形ABCD中,∠DAB=60°,∴∠BAO=30°.
∴BO=AB=1,AO=.
又∵AE=AG=,∴EO=2.
∴EB==.
由(1)得EB=GD,∴GD=.
9.证明:∵A',B'分别是OA,OB的中点,
∴A'B'∥AB,A'B'=AB.
∴∠OA'B'=∠OAB,=.
同理,∠OA'D'=∠OAD,=,
∴∠B'A'D'=∠BAD,=.
同理,∠A'D'C'=∠ADC,∠D'C'B'=∠DCB,∠C'B'A'=∠CBA,
==,
∴四边形ABCD∽四边形A'B'C'D'.
10.2
11.解:(1)因为矩形纸片A的长和宽的比是,将矩形A对折,得矩形A1,再将矩形A1对折,得矩形A2,依次对折下去得矩形A3,A4,…,An,则所得矩形的长与宽的比始终为∶1.又矩形的四个内角都为90°,所以矩形A,A1,A2,A3,A4,…,An都相似.
(2)因为矩形A的长和宽的比为(q因为p≠q,所以≠,所以所得的矩形A,A1,A2,A3,A4,…,An不相似.
由(1)知当=,即p=q时,所得的矩形A,A1,A2,A3,A4,…,An相似.
故只有矩形纸片A的长和宽的比是时,所得矩形才相似.
命题点 1 识别相似图形
1.观察下列每组图形,相似图形是 ( )
2.下列每组两个图形不一定相似的是 ( )
A.两个正方形 B.两个等腰直角三角形
C.两个等边三角形 D.两个等腰三角形
3.在如图所示的三个矩形中,相似的是( )
A.甲和乙 B.甲和丙
C.乙和丙 D.甲、乙和丙
4.如图矩形ABCD的长AB=30,宽BC=20.
(1)如图①,若矩形ABCD四周有宽为1的环形区域,则图中所形成的矩形ABCD与矩形A'B'C'D'相似吗 请说明理由;
(2)如图②,当x为多少时,图中的矩形ABCD与矩形A'B'C'D'相似
命题点 2 利用相似多边形的定义求值
5.用同一张图片打印出来的两张照片,一张为2寸,另一张为6寸,则这两张照片上的像的相似比是 .
6.如图在正方形ABCD中,E是对角线BD上的一点,BE=BC,过点E作EF⊥AB,EG⊥BC,垂足分别为F,G,则正方形FBGE与正方形ABCD的相似比为 .
7.如图四边形ABCD为平行四边形,AE平分∠BAD交BC于点E,过点E作EF∥AB,交AD于点F,连接BF.
(1)求证:BF平分∠ABC;
(2)若AB=6,且四边形ABCD∽四边形CEFD,求BC的长.
8.如图E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且菱形AEFG∽菱形ABCD,连接EB,GD.
(1)求证:EB=GD;
(2)若∠DAB=60°,AB=2,AG=,求GD的长.
命题点 3 利用定义判定多边形相似
9.如图四边形ABCD的对角线相交于点O,A',B',C',D'分别是OA,OB,OC,OD的中点.
求证:四边形ABCD∽四边形A'B'C'D'.
10.彼此相似的正方形A1B1C1O,A2B2C2C1,A3B3C3C2如图所示,点A1,A2,A3和点C1,C2,C3分别在直线y=kx+b(k>0)和x轴上,点B3的坐标是,,则5k-bk的值为 .
11.如.
(1)已知矩形纸片A,它的长和宽的比是,将矩形A对折,得矩形A1,再将矩形A1对折,得矩形A2,依次对折下去得矩形A3,A4,…,An,那么矩形A,A1,A2,A3,A4,…,An都相似吗
(2)如果矩形A的长和宽的比为(q
3 相似多边形
1.C 2.D 3.A
4.解:(1)不相似.
理由:∵AB=30,A'B'=28,BC=20,B'C'=18,
而≠,∴两个矩形不相似.
(2)若矩形ABCD与矩形A'B'C'D'相似,有以下两种情况:
①=,即=,
解得x=1.5;
②=,即=,解得x=9.
∴当x为1.5或9时,矩形ABCD与矩形A'B'C'D'相似.
5.1∶3
6. 设BG=x,
则BE=x.
∵BE=BC,
∴BC=x.
则正方形FBGE与正方形ABCD的相似比=BG∶BC=x∶x=∶2.
7.解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠FAE=∠AEB.
∵AE平分∠BAD,∴∠FAE=∠BAE.
∴∠BAE=∠AEB.∴AB=EB.
∵AD∥BC,EF∥AB,
∴四边形ABEF是平行四边形.
又∵AB=EB,∴四边形ABEF是菱形.
∴BF平分∠ABC.
(2)∵EF∥AB,AB∥CD,∴EF∥CD.
又∵AD∥BC,∴四边形CEFD是平行四边形.
由(1)知四边形ABEF是菱形,∴EF=BE=AB=6.
∵四边形ABCD∽四边形CEFD,
∴=,即=,
解得BC=3+3(负值已舍去).
8.解:(1)证明:∵菱形AEFG∽菱形ABCD,
∴AB=AD,AE=AG,∠EAG=∠BAD.
∴∠EAB=∠GAD.
∴△EAB≌△GAD.则EB=GD.
(2)过点B作BO⊥AC于点O.
∵在菱形ABCD中,∠DAB=60°,∴∠BAO=30°.
∴BO=AB=1,AO=.
又∵AE=AG=,∴EO=2.
∴EB==.
由(1)得EB=GD,∴GD=.
9.证明:∵A',B'分别是OA,OB的中点,
∴A'B'∥AB,A'B'=AB.
∴∠OA'B'=∠OAB,=.
同理,∠OA'D'=∠OAD,=,
∴∠B'A'D'=∠BAD,=.
同理,∠A'D'C'=∠ADC,∠D'C'B'=∠DCB,∠C'B'A'=∠CBA,
==,
∴四边形ABCD∽四边形A'B'C'D'.
10.2
11.解:(1)因为矩形纸片A的长和宽的比是,将矩形A对折,得矩形A1,再将矩形A1对折,得矩形A2,依次对折下去得矩形A3,A4,…,An,则所得矩形的长与宽的比始终为∶1.又矩形的四个内角都为90°,所以矩形A,A1,A2,A3,A4,…,An都相似.
(2)因为矩形A的长和宽的比为(q
由(1)知当=,即p=q时,所得的矩形A,A1,A2,A3,A4,…,An相似.
故只有矩形纸片A的长和宽的比是时,所得矩形才相似.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
