北师大版数学九年级上册同步提优训练:4.5相似三角形判定定理的证明(word版含答案)
文档属性
| 名称 | 北师大版数学九年级上册同步提优训练:4.5相似三角形判定定理的证明(word版含答案) | 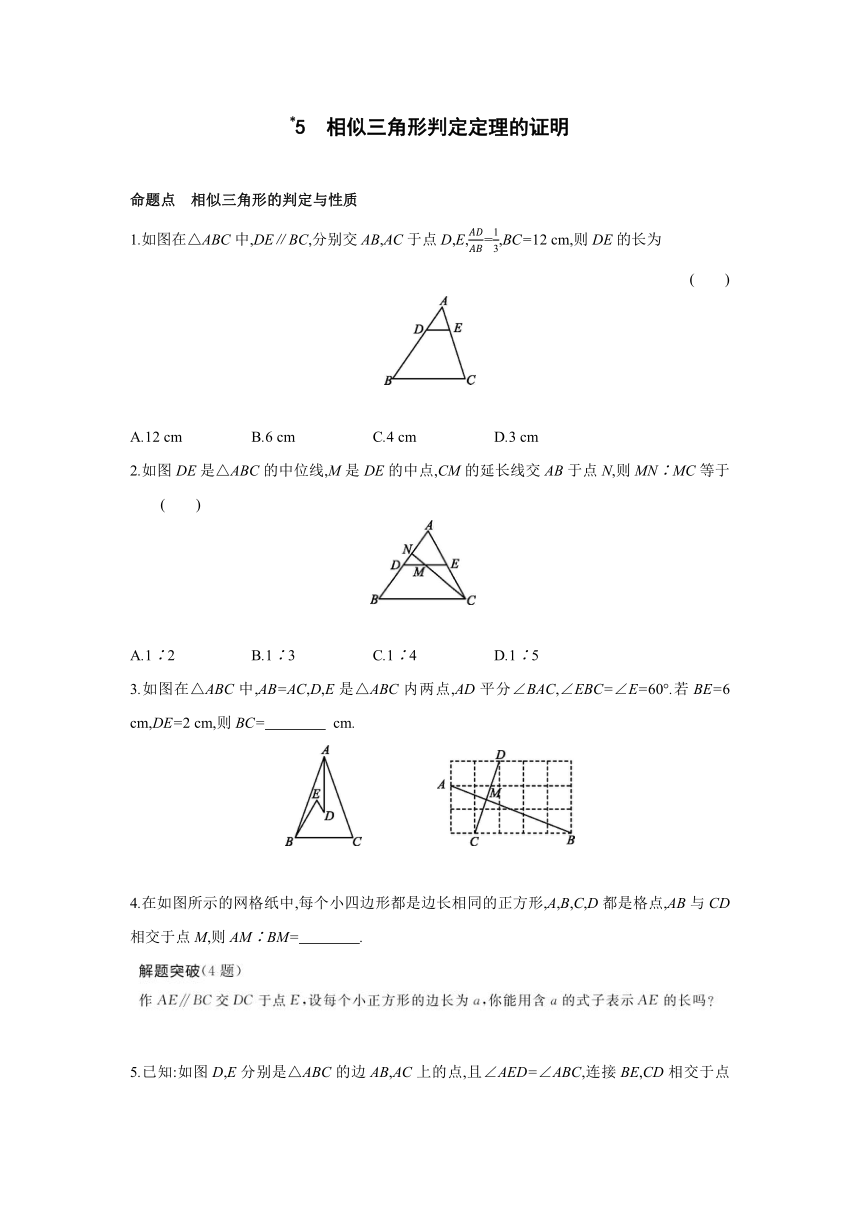 | |
| 格式 | docx | ||
| 文件大小 | 260.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-11 23:02:45 | ||
图片预览



文档简介
*5 相似三角形判定定理的证明
命题点 相似三角形的判定与性质
1.如图在△ABC中,DE∥BC,分别交AB,AC于点D,E,=,BC=12 cm,则DE的长为
( )
A.12 cm B.6 cm C.4 cm D.3 cm
2.如图DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于点N,则MN∶MC等于 ( )
A.1∶2 B.1∶3 C.1∶4 D.1∶5
3.如图在△ABC中,AB=AC,D,E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°.若BE=6 cm,DE=2 cm,则BC= cm.
4.在如图所示的网格纸中,每个小四边形都是边长相同的正方形,A,B,C,D都是格点,AB与CD相交于点M,则AM∶BM= .
5.已知:如图D,E分别是△ABC的边AB,AC上的点,且∠AED=∠ABC,连接BE,CD相交于点F.
(1)求证:∠ABE=∠ACD;
(2)如果ED=EC,求证:=.
6.(2020上海)已知:如图在菱形ABCD中,点E,F分别在边AB,AD上,BE=DF,CE的延长线交DA的延长线于点G,CF的延长线交BA的延长线于点H.
(1)求证:△BEC∽△BCH;
(2)如果BE2=AB·AE,求证:AG=DF.
7.已知:如图在△ABC中,AB=AC,AD是边BC上的中线,BE⊥AC于点E,AD与BE交于点H.
(1)求证:BD2=DH·AD;
(2)过点C作CF∥AB交BE的延长线于点F.求证:HB2=HE·HF.
8.(1)如(a),在△ABC中,点D,E,Q分别在AB,AC,BC上,且DE∥BC,AQ交DE于点P.
求证:=.
(2)如图(b)(c),在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点.
①如图(b),若AB=AC=1,直接写出MN的长;
②如图(c),求证:MN2=DM·EN.
答案
*5 相似三角形判定定理的证明
1.C ∵DE∥BC,∴∠ADE=∠ABC.
又∵∠A=∠A,∴△ADE∽△ABC.∴=.
∴DE=4 cm.故选C.
2.B ∵DE是△ABC的中位线,M是DE的中点,∴DM∥BC,DM=ME=BC.∴∠NDM=∠B,∠NMD=∠NCB.∴△NDM∽△NBC.则==.∴=.故选B.
3.8 如图,过点E作EM⊥BC于点M,分别延长AD,ED交BC于点F,H.由题意可得DF∥EM,△EBH为等边三角形,所以BE=BH=EH=6,HM=3,=,所以HF=2,所以BF=4,所以BC=8 cm.
4.5∶12 设每个小正方形的边长为a.如图,作AE∥BC交DC于点E,交DN于点F.
则△DEF∽△DCN,△AME∽△BMC,
∴==.∴EF=a.
∵AF=2a,∴AE=a.
易得△AME∽△BMC,∴===.
故答案为5∶12.
5.证明:(1)∵∠AED=∠ABC,∠A=∠A,
∴△ADE∽△ACB,
∴=.
又∵∠A=∠A,∴△ADC∽△AEB,
∴∠ABE=∠ACD.
(2)∵ED=EC,∴∠EDC=∠ECD.
又∵∠EBD=∠ECD,∴∠EDC=∠EBD.
又∵∠DEF=∠DEB,
∴△EDF∽△EBD,
∴==,则2=·,
∴=.
6.证明:(1)∵四边形ABCD是菱形,
∴CD=CB,∠D=∠B,CD∥AB.
又∵DF=BE,
∴△CDF≌△CBE(SAS),
∴∠DCF=∠BCE.
∵CD∥BH,
∴∠H=∠DCF,
∴∠H=∠BCE.
又∵∠B=∠B,
∴△BEC∽△BCH.
(2)∵BE2=AB·AE,
∴=.
∵CB∥DG,
∴△CBE∽△GAE,
∴=,
∴=.
∵BC=AB,
∴AG=BE.
又∵DF=BE,
∴AG=DF.
7.证明:(1)∵在△ABC中,AB=AC,AD是边BC上的中线,
∴AD⊥BC,∠BAD=∠CAD,
∴∠ADB=90°.
∵BE⊥AC于点E,∴∠HEA=90°.
又∵∠AHE=∠BHD,∴∠CAD=∠DBH,
∴∠BAD=∠DBH,∴△BAD∽△HBD.
则=,
∴BD2=DH·AD.
(2)连接HC,如图.
易得AD垂直平分BC,∴HB=HC,
∴∠HBC=∠HCB.
∵AB=AC,∴∠ABC=∠ACB.
∵∠BEC=90°,∴∠HBC+∠ACB=90°,
∴∠HCB+∠ABC=90°.
∵CF∥AB,∴∠ABC+∠HCB+∠HCF=180°,
∴∠HCF=90°.
∵∠HCF=∠HEC=90°,∠FHC=∠CHE,
∴△FHC∽△CHE,
∴=,∴=,
则HB2=HE·HF.
8.解:(1)证明:∵DE∥BC,
∴∠ADP=∠B,∠APD=∠AQB,
∠APE=∠AQC,∠AEP=∠C.
∴△ADP∽△ABQ,△APE∽△AQC.
∴=,=.
∴=.
(2)①MN=.
②证明:∵∠B+∠C=180°-∠BAC=90°,∠CEF+∠C=∠EFG=90°,
∴∠B=∠CEF.
又∵∠BGD=∠EFC=90°,
∴△BGD∽△EFC.
∴=.
∴DG·EF=CF·BG.
又∵DG=GF=EF,
∴GF2=CF·BG.
同(1)可得==,
∴2=·.
∴MN2=DM·EN.
命题点 相似三角形的判定与性质
1.如图在△ABC中,DE∥BC,分别交AB,AC于点D,E,=,BC=12 cm,则DE的长为
( )
A.12 cm B.6 cm C.4 cm D.3 cm
2.如图DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于点N,则MN∶MC等于 ( )
A.1∶2 B.1∶3 C.1∶4 D.1∶5
3.如图在△ABC中,AB=AC,D,E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°.若BE=6 cm,DE=2 cm,则BC= cm.
4.在如图所示的网格纸中,每个小四边形都是边长相同的正方形,A,B,C,D都是格点,AB与CD相交于点M,则AM∶BM= .
5.已知:如图D,E分别是△ABC的边AB,AC上的点,且∠AED=∠ABC,连接BE,CD相交于点F.
(1)求证:∠ABE=∠ACD;
(2)如果ED=EC,求证:=.
6.(2020上海)已知:如图在菱形ABCD中,点E,F分别在边AB,AD上,BE=DF,CE的延长线交DA的延长线于点G,CF的延长线交BA的延长线于点H.
(1)求证:△BEC∽△BCH;
(2)如果BE2=AB·AE,求证:AG=DF.
7.已知:如图在△ABC中,AB=AC,AD是边BC上的中线,BE⊥AC于点E,AD与BE交于点H.
(1)求证:BD2=DH·AD;
(2)过点C作CF∥AB交BE的延长线于点F.求证:HB2=HE·HF.
8.(1)如(a),在△ABC中,点D,E,Q分别在AB,AC,BC上,且DE∥BC,AQ交DE于点P.
求证:=.
(2)如图(b)(c),在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点.
①如图(b),若AB=AC=1,直接写出MN的长;
②如图(c),求证:MN2=DM·EN.
答案
*5 相似三角形判定定理的证明
1.C ∵DE∥BC,∴∠ADE=∠ABC.
又∵∠A=∠A,∴△ADE∽△ABC.∴=.
∴DE=4 cm.故选C.
2.B ∵DE是△ABC的中位线,M是DE的中点,∴DM∥BC,DM=ME=BC.∴∠NDM=∠B,∠NMD=∠NCB.∴△NDM∽△NBC.则==.∴=.故选B.
3.8 如图,过点E作EM⊥BC于点M,分别延长AD,ED交BC于点F,H.由题意可得DF∥EM,△EBH为等边三角形,所以BE=BH=EH=6,HM=3,=,所以HF=2,所以BF=4,所以BC=8 cm.
4.5∶12 设每个小正方形的边长为a.如图,作AE∥BC交DC于点E,交DN于点F.
则△DEF∽△DCN,△AME∽△BMC,
∴==.∴EF=a.
∵AF=2a,∴AE=a.
易得△AME∽△BMC,∴===.
故答案为5∶12.
5.证明:(1)∵∠AED=∠ABC,∠A=∠A,
∴△ADE∽△ACB,
∴=.
又∵∠A=∠A,∴△ADC∽△AEB,
∴∠ABE=∠ACD.
(2)∵ED=EC,∴∠EDC=∠ECD.
又∵∠EBD=∠ECD,∴∠EDC=∠EBD.
又∵∠DEF=∠DEB,
∴△EDF∽△EBD,
∴==,则2=·,
∴=.
6.证明:(1)∵四边形ABCD是菱形,
∴CD=CB,∠D=∠B,CD∥AB.
又∵DF=BE,
∴△CDF≌△CBE(SAS),
∴∠DCF=∠BCE.
∵CD∥BH,
∴∠H=∠DCF,
∴∠H=∠BCE.
又∵∠B=∠B,
∴△BEC∽△BCH.
(2)∵BE2=AB·AE,
∴=.
∵CB∥DG,
∴△CBE∽△GAE,
∴=,
∴=.
∵BC=AB,
∴AG=BE.
又∵DF=BE,
∴AG=DF.
7.证明:(1)∵在△ABC中,AB=AC,AD是边BC上的中线,
∴AD⊥BC,∠BAD=∠CAD,
∴∠ADB=90°.
∵BE⊥AC于点E,∴∠HEA=90°.
又∵∠AHE=∠BHD,∴∠CAD=∠DBH,
∴∠BAD=∠DBH,∴△BAD∽△HBD.
则=,
∴BD2=DH·AD.
(2)连接HC,如图.
易得AD垂直平分BC,∴HB=HC,
∴∠HBC=∠HCB.
∵AB=AC,∴∠ABC=∠ACB.
∵∠BEC=90°,∴∠HBC+∠ACB=90°,
∴∠HCB+∠ABC=90°.
∵CF∥AB,∴∠ABC+∠HCB+∠HCF=180°,
∴∠HCF=90°.
∵∠HCF=∠HEC=90°,∠FHC=∠CHE,
∴△FHC∽△CHE,
∴=,∴=,
则HB2=HE·HF.
8.解:(1)证明:∵DE∥BC,
∴∠ADP=∠B,∠APD=∠AQB,
∠APE=∠AQC,∠AEP=∠C.
∴△ADP∽△ABQ,△APE∽△AQC.
∴=,=.
∴=.
(2)①MN=.
②证明:∵∠B+∠C=180°-∠BAC=90°,∠CEF+∠C=∠EFG=90°,
∴∠B=∠CEF.
又∵∠BGD=∠EFC=90°,
∴△BGD∽△EFC.
∴=.
∴DG·EF=CF·BG.
又∵DG=GF=EF,
∴GF2=CF·BG.
同(1)可得==,
∴2=·.
∴MN2=DM·EN.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
