2022—2023学年人教版数学七年级上册 1.2.1 有理数 课件(共16张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学七年级上册 1.2.1 有理数 课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 279.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-11 22:29:14 | ||
图片预览






文档简介
(共16张PPT)
1.2.1 有理数
第一章 有理数
导入新课
讲授新课
当堂练习
课堂小结
1.2 有理数
七年级数学上 教学课件
知识回顾
1.通过上节课的知识,你知道除了正数外还有什么数?
0和负数
0既不是正数,也不是负数
2.用正数和负数来表示具有相反意义的量
如,一个物体向右移动5m,记作物体移动+5m
一个物体向左移动3m,记作物体移动
原地不动,记作移动 。
-3m
0m
问题1:
1,
0.1,
-1,
,
-3,
2,
-0.5,
0,
2.25,
在以上各数中,哪些是在小学里学过的数
哪些是在中学里学过的数
你能试着将他们分类吗
,
,
,-
小学学过的数:
中学学过的数:
讲授新课
有理数的概念
一
我们以前学过的数,
特别提示:0既不是正数,也不是负数!
还有小数呢?
-1,-2,-3,…称为负整数;
像1,2,3,…称为正整数;
,…称为负分数.
,…称为正分数.
那么在以上这些数的前面添上“-”号后,
1.目前我们所学的小数有哪几类?你能尝试把它们化为
分数吗?
2.0.1,-0.5,5.32,-150.25, 等为什么被列为分数?
它们都可以化为分数:
思考:
有限小数,无限循环小数,除π外均能化为分数
这些能化为分数的小数,都看作为分数
正整数、零和负整数统称整数.
整数和分数统称为
有理数.
正分数和负分数统称分数.
概念归纳
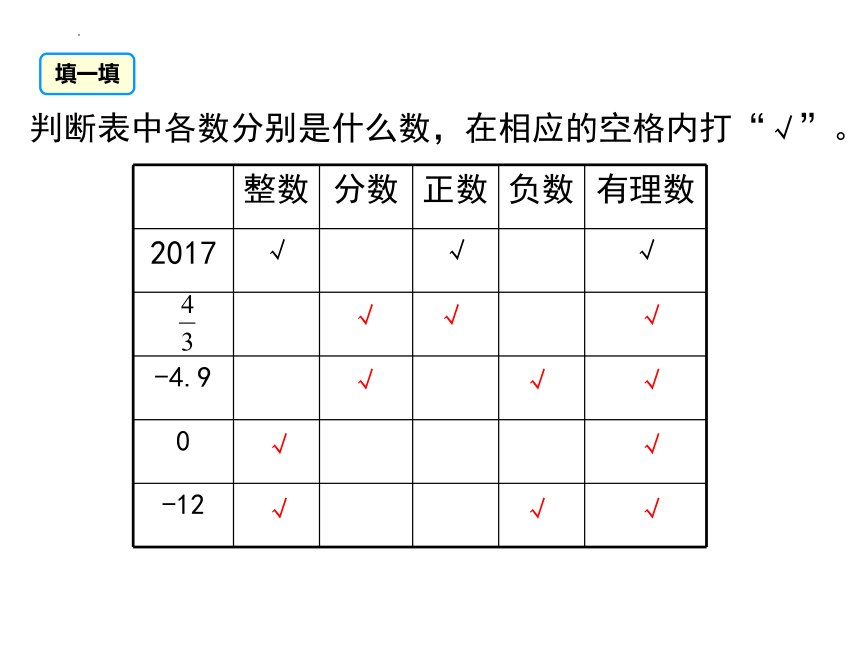
判断表中各数分别是什么数,在相应的空格内打“√”。
整数 分数 正数 负数 有理数
2017 √ √ √
-4.9
0
-12
√ √ √
√ √ √
√ √
√ √ √
填一填
有理数的分类
二
你能根据有理数的定义对有理数分类吗?
负分数
正分数
负整数
正整数
零
整数
分数
有理数
负分数
正分数
负整数
正整数
零
整数
分数
有理数
自然数
按定义分类
有理数的分类
二
还有其他方法对有理数分类吗?
正有理数
负有理数
正分数
负分数
负整数
正整数
0
有理数
按符号分类
探究总结
有限小数和无限循环小数都是分数,所以也是有理数。
无限不循环小数(如 π )不是分数,就不是有理数。
质疑探索
学了有理数的分类后,聪明的你想过没有——有没有一些数不是有理数呢?
有理数分类的几点注意:
1.如 能约分成整数的数_____(填“能”或
“不能”)算做分数;
不能
2.无限不循环小数不是有理数,如π;(无理数)
3.整数中除了正整数和负整数,还有_____.
0
有理数还有其他的分类方法吗?
填一填:
(1)既是分数又是负数的数是_______;
(2)非负数包括________和_______;
(3)非正数包括________和_______;
(4)非负整数包括________和_______;又称为________;
(5)非负分数包括________和_______;
(6)非正分数包括________和_______.
负分数
正数
0
0
负数
自然数
正整数
0
整数
正分数
整数
负分数
1.把下列各数填入它所属于的集合的圈内:
15, , , , ,
0.1, , , 123, 2.33.
正分数集合 负整数集合
正整数集合 负分数集合
15,
123
,
,0.1,2.33
例1:下列说法:
①0是整数;
② 是负分数;
③4.2不是正数;
④自然数一定是正数;
⑤负分数一定是负有理数.
其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
C
典例精析
例2:把下列各数填在相应的集合中:
正数集合:{ };
负数集合:{ };
分数集合:{ };
整数集合:{ };
非负有理数集合:{ };
有理数集合:{ }.
易错提醒:1.像 这种可以先化简成整数的数是
整数不是分数;2.π大于0是正数不是正有理数.
1.到现在为止,我们学过的数(π 除外)都是有
理数.
2.有理数的分类
有理数
整数
分数
负整数
负分数
正分数
正整数
0
正有理数
负有理数
正分数
负分数
负整数
正整数
0
有理数
3.注意0的特殊性,分类时不要遗漏0.
课堂小结
1.2.1 有理数
第一章 有理数
导入新课
讲授新课
当堂练习
课堂小结
1.2 有理数
七年级数学上 教学课件
知识回顾
1.通过上节课的知识,你知道除了正数外还有什么数?
0和负数
0既不是正数,也不是负数
2.用正数和负数来表示具有相反意义的量
如,一个物体向右移动5m,记作物体移动+5m
一个物体向左移动3m,记作物体移动
原地不动,记作移动 。
-3m
0m
问题1:
1,
0.1,
-1,
,
-3,
2,
-0.5,
0,
2.25,
在以上各数中,哪些是在小学里学过的数
哪些是在中学里学过的数
你能试着将他们分类吗
,
,
,-
小学学过的数:
中学学过的数:
讲授新课
有理数的概念
一
我们以前学过的数,
特别提示:0既不是正数,也不是负数!
还有小数呢?
-1,-2,-3,…称为负整数;
像1,2,3,…称为正整数;
,…称为负分数.
,…称为正分数.
那么在以上这些数的前面添上“-”号后,
1.目前我们所学的小数有哪几类?你能尝试把它们化为
分数吗?
2.0.1,-0.5,5.32,-150.25, 等为什么被列为分数?
它们都可以化为分数:
思考:
有限小数,无限循环小数,除π外均能化为分数
这些能化为分数的小数,都看作为分数
正整数、零和负整数统称整数.
整数和分数统称为
有理数.
正分数和负分数统称分数.
概念归纳
判断表中各数分别是什么数,在相应的空格内打“√”。
整数 分数 正数 负数 有理数
2017 √ √ √
-4.9
0
-12
√ √ √
√ √ √
√ √
√ √ √
填一填
有理数的分类
二
你能根据有理数的定义对有理数分类吗?
负分数
正分数
负整数
正整数
零
整数
分数
有理数
负分数
正分数
负整数
正整数
零
整数
分数
有理数
自然数
按定义分类
有理数的分类
二
还有其他方法对有理数分类吗?
正有理数
负有理数
正分数
负分数
负整数
正整数
0
有理数
按符号分类
探究总结
有限小数和无限循环小数都是分数,所以也是有理数。
无限不循环小数(如 π )不是分数,就不是有理数。
质疑探索
学了有理数的分类后,聪明的你想过没有——有没有一些数不是有理数呢?
有理数分类的几点注意:
1.如 能约分成整数的数_____(填“能”或
“不能”)算做分数;
不能
2.无限不循环小数不是有理数,如π;(无理数)
3.整数中除了正整数和负整数,还有_____.
0
有理数还有其他的分类方法吗?
填一填:
(1)既是分数又是负数的数是_______;
(2)非负数包括________和_______;
(3)非正数包括________和_______;
(4)非负整数包括________和_______;又称为________;
(5)非负分数包括________和_______;
(6)非正分数包括________和_______.
负分数
正数
0
0
负数
自然数
正整数
0
整数
正分数
整数
负分数
1.把下列各数填入它所属于的集合的圈内:
15, , , , ,
0.1, , , 123, 2.33.
正分数集合 负整数集合
正整数集合 负分数集合
15,
123
,
,0.1,2.33
例1:下列说法:
①0是整数;
② 是负分数;
③4.2不是正数;
④自然数一定是正数;
⑤负分数一定是负有理数.
其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
C
典例精析
例2:把下列各数填在相应的集合中:
正数集合:{ };
负数集合:{ };
分数集合:{ };
整数集合:{ };
非负有理数集合:{ };
有理数集合:{ }.
易错提醒:1.像 这种可以先化简成整数的数是
整数不是分数;2.π大于0是正数不是正有理数.
1.到现在为止,我们学过的数(π 除外)都是有
理数.
2.有理数的分类
有理数
整数
分数
负整数
负分数
正分数
正整数
0
正有理数
负有理数
正分数
负分数
负整数
正整数
0
有理数
3.注意0的特殊性,分类时不要遗漏0.
课堂小结
