人教版(新)九上-24.2.2 直线和圆的位置关系 第一课时【优质课件】
文档属性
| 名称 | 人教版(新)九上-24.2.2 直线和圆的位置关系 第一课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 14:08:09 | ||
图片预览








文档简介
(共26张PPT)
24.2.2 直线和圆的位置关系
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
本课是在研究点和圆的位置关系之后,进一步研究由点组成的直线和圆的位置关系.
新课精讲
探索新知
1
知识点
直线与圆的位置关系的判定
问 题(一)
(1)如图(1),如果我们把太阳看作一个圆,把地平线看作一条直线,太阳升起的过程中,太阳和地平线会有几种位置关系?由此你能得出直线和圆的位置关系吗?
探索新知
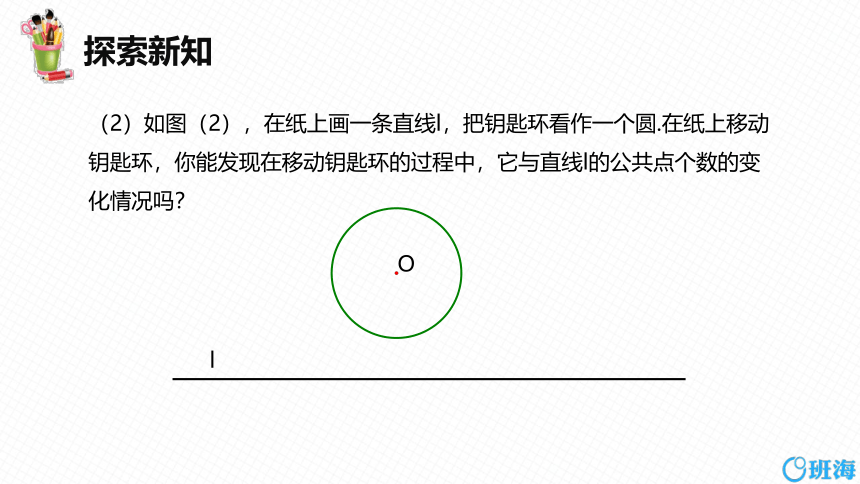
(2)如图(2),在纸上画一条直线l,把钥匙环看作一个圆.在纸上移动钥匙环,你能发现在移动钥匙环的过程中,它与直线l的公共点个数的变化情况吗?
l
O
探索新知
问 题(二)
思考:设⊙O的半径为r,圆心O到直线l的距离为d,在直线和圆的不同位置关系中,你能根据d与r的大小关系确定直线和圆的位置关系吗?
探索新知
例1 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=4 cm,以点C为圆心,2 cm为半径作圆,则⊙C与AB的位置关系是( )
A.相离 B.相切
C.相交 D.相切或相交
导引:本例若通过看公共点的个数来判断,作图稍有不准,就会产生误判,因此需通过比较圆心到直线的距离与半径的大小来判断.如图,过点C作CH⊥AB于点H,在Rt△CHB中,易得CH=2 cm,即d=r=2 cm,所以⊙C与AB的位置关系是相切.
B
探索新知
归 纳
如果画图后直线和圆的位置关系不明显,一般不选用公共点个数来判断直线和圆的位置关系.应采用比较圆心到直线的距离与半径大小的方法来确定它们之间的位置关系;在没有给出d与r的具体数值的情况下,可先利用图形条件及性质求出d与r的值,再通过比较大小确定其位置关系.
典题精讲
在平面直角坐标系中,以点(-3,4)为圆心,4为半径的圆( )
A.与x轴相交,与y轴相切
B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相离
D.与x轴相切,与y轴相交
C
探索新知
这条直线叫做圆的割线,公共点叫直线和圆的交点.
直线和圆没有公共点时,叫做直线和圆相离.
直线和圆有唯一公共点时,叫做直线和圆相切.
直线和圆有两个公共点时,叫做直线和圆相交.
这条直线叫做圆的切线,这个点叫做切点.
l
O
l
O
A
l
O
A
B
2
知识点
直线与圆的位置关系的性质
探索新知
总 结
1. 直线和圆相离→d>r;
2. 直线和圆相切→d=r;
3. 直线和圆相交→d<r.
探索新知
例2 在Rt△ABC中,AC=3 cm,BC=4 cm,∠ACB=90°.若以点C为圆
心,r为半径的圆与直线AB不相离,求r的取值范围.
⊙C与直线AB不相离,即⊙C与直线AB相交或相切,因此只需点C到直线AB的距离小于或等于r.
导引:
解:如图,过点C作CD⊥AB于点D. 在Rt△ABC中,
AC=3 cm,BC=4 cm,∠ACB=90°,
∴AB=
又∵S△ABC= AB CD= AC BC,
∴CD=2.4 cm. ∴r≥2.4 cm.
探索新知
总 结
(1)直线和圆的位置关系的应用过程实质是一种数形结合思想的转化过程,它始终是“数”:圆心到直线的距离与圆的半径大小,与“形”:直线和圆的位置关系之间的相互转化.
(2)圆心到直线的距离通常用勾股定理与面积相等法求出.
典题精讲
如图,∠O=30°,P为边OA上的一点,且OP=5,若以P为圆心,r为半径的圆与射线OB只有一个公共点,则半径r的取值范围是( )
A.r=5
B.r=
≤r<5
D.r= 或r>5
B
学以致用
小试牛刀
1.
已知⊙O的直径等于12 cm,圆心O到直线l的距离为5 cm,则直线l与⊙O的公共点个数为( )
A.0 B.1 C.2 D.无法确定
C
已知⊙O的半径为10cm,如果圆心O到一条直线的距离为10cm,那么这条直线和这个圆的位置关系为( )
A. 相离 B. 相切
C. 相交 D. 无法确定
B
2.
小试牛刀
已知⊙O的半径是5,直线l是⊙O的切线,则点O到直线l的距离是( )
A.2.5 B.3
C.5 D.10
4.
3.
已知直线l与半径为r的⊙O相交,且点O到直线l的距离为6,则r的取值范围是( )
A.r<6 B.r=6
C.r>6 D.r≥6
C
C
小试牛刀
如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=18°,则∠CDA=( )
A.60° B.123°
C.126° D.54°
6.
5.
两圆的半径分别为7和1,圆心距为10,则其内公切线长和外公切线长分别为( )
A.6,8 B.6,10
C.8,2 D.8,6
A
C
小试牛刀
下列说法正确的是( )
A.垂直于切线的直线必经过切点
B.垂直于半径的直线是圆的切线
C.圆的切线垂直于经过切点的半径
D.垂直于切线的直线必过圆心
8.
7.
如图,在半径为 5 cm的⊙O中,直线 1 交⊙O于A、B两点,且弦AB =8 cm,要使直线 1 与⊙O相切,则需要将直线l平移( )
A.1cm或9cm B.2cm或8cm
C.2cm D.3cm
B
C
小试牛刀
如图,AB是⊙O的直径,AE平分∠BAF交⊙O交于E,过E点作直线与AF垂直,交AF延长线于D点,且交AB的延长线于C点.
(1)求证:CD是⊙O的切线;
9.
证明:连接OE, 则∠OAE=∠OEA.
由∠OAE=∠EAD ,得∠OEA=∠EAD,
所以OE∥AD.
因为AD⊥CD, 所以OE⊥CD,
所以CD是⊙O的切线.
小试牛刀
如图,AB是⊙O的直径,AE平分∠BAF交⊙O交于E,过E点作直线与AF垂直,交AF延长线于D点,且交AB的延长线于C点.
(2)若∠C=30°,DE= ,求⊙O的直径.
9.
解:过点O作OG⊥AD于点G.则∠AOG=∠ACD=30°,
四边形OEDG为矩形.
∴OG=ED=.
∴OA=2, ∴⊙O的直径是4.
课堂小结
课堂小结
1.直线和圆的位置关系:相交、相切、相离.
(1)从公共点数来判断;
(2)从d与r间的数量关系来判断.
2.直线和圆的位置关系的性质与判定:
(1)直线和圆相离 d>r;
(2)直线和圆相切 d=r;
(3)直线和圆相交 d<r.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
24.2.2 直线和圆的位置关系
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
本课是在研究点和圆的位置关系之后,进一步研究由点组成的直线和圆的位置关系.
新课精讲
探索新知
1
知识点
直线与圆的位置关系的判定
问 题(一)
(1)如图(1),如果我们把太阳看作一个圆,把地平线看作一条直线,太阳升起的过程中,太阳和地平线会有几种位置关系?由此你能得出直线和圆的位置关系吗?
探索新知
(2)如图(2),在纸上画一条直线l,把钥匙环看作一个圆.在纸上移动钥匙环,你能发现在移动钥匙环的过程中,它与直线l的公共点个数的变化情况吗?
l
O
探索新知
问 题(二)
思考:设⊙O的半径为r,圆心O到直线l的距离为d,在直线和圆的不同位置关系中,你能根据d与r的大小关系确定直线和圆的位置关系吗?
探索新知
例1 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=4 cm,以点C为圆心,2 cm为半径作圆,则⊙C与AB的位置关系是( )
A.相离 B.相切
C.相交 D.相切或相交
导引:本例若通过看公共点的个数来判断,作图稍有不准,就会产生误判,因此需通过比较圆心到直线的距离与半径的大小来判断.如图,过点C作CH⊥AB于点H,在Rt△CHB中,易得CH=2 cm,即d=r=2 cm,所以⊙C与AB的位置关系是相切.
B
探索新知
归 纳
如果画图后直线和圆的位置关系不明显,一般不选用公共点个数来判断直线和圆的位置关系.应采用比较圆心到直线的距离与半径大小的方法来确定它们之间的位置关系;在没有给出d与r的具体数值的情况下,可先利用图形条件及性质求出d与r的值,再通过比较大小确定其位置关系.
典题精讲
在平面直角坐标系中,以点(-3,4)为圆心,4为半径的圆( )
A.与x轴相交,与y轴相切
B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相离
D.与x轴相切,与y轴相交
C
探索新知
这条直线叫做圆的割线,公共点叫直线和圆的交点.
直线和圆没有公共点时,叫做直线和圆相离.
直线和圆有唯一公共点时,叫做直线和圆相切.
直线和圆有两个公共点时,叫做直线和圆相交.
这条直线叫做圆的切线,这个点叫做切点.
l
O
l
O
A
l
O
A
B
2
知识点
直线与圆的位置关系的性质
探索新知
总 结
1. 直线和圆相离→d>r;
2. 直线和圆相切→d=r;
3. 直线和圆相交→d<r.
探索新知
例2 在Rt△ABC中,AC=3 cm,BC=4 cm,∠ACB=90°.若以点C为圆
心,r为半径的圆与直线AB不相离,求r的取值范围.
⊙C与直线AB不相离,即⊙C与直线AB相交或相切,因此只需点C到直线AB的距离小于或等于r.
导引:
解:如图,过点C作CD⊥AB于点D. 在Rt△ABC中,
AC=3 cm,BC=4 cm,∠ACB=90°,
∴AB=
又∵S△ABC= AB CD= AC BC,
∴CD=2.4 cm. ∴r≥2.4 cm.
探索新知
总 结
(1)直线和圆的位置关系的应用过程实质是一种数形结合思想的转化过程,它始终是“数”:圆心到直线的距离与圆的半径大小,与“形”:直线和圆的位置关系之间的相互转化.
(2)圆心到直线的距离通常用勾股定理与面积相等法求出.
典题精讲
如图,∠O=30°,P为边OA上的一点,且OP=5,若以P为圆心,r为半径的圆与射线OB只有一个公共点,则半径r的取值范围是( )
A.r=5
B.r=
≤r<5
D.r= 或r>5
B
学以致用
小试牛刀
1.
已知⊙O的直径等于12 cm,圆心O到直线l的距离为5 cm,则直线l与⊙O的公共点个数为( )
A.0 B.1 C.2 D.无法确定
C
已知⊙O的半径为10cm,如果圆心O到一条直线的距离为10cm,那么这条直线和这个圆的位置关系为( )
A. 相离 B. 相切
C. 相交 D. 无法确定
B
2.
小试牛刀
已知⊙O的半径是5,直线l是⊙O的切线,则点O到直线l的距离是( )
A.2.5 B.3
C.5 D.10
4.
3.
已知直线l与半径为r的⊙O相交,且点O到直线l的距离为6,则r的取值范围是( )
A.r<6 B.r=6
C.r>6 D.r≥6
C
C
小试牛刀
如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=18°,则∠CDA=( )
A.60° B.123°
C.126° D.54°
6.
5.
两圆的半径分别为7和1,圆心距为10,则其内公切线长和外公切线长分别为( )
A.6,8 B.6,10
C.8,2 D.8,6
A
C
小试牛刀
下列说法正确的是( )
A.垂直于切线的直线必经过切点
B.垂直于半径的直线是圆的切线
C.圆的切线垂直于经过切点的半径
D.垂直于切线的直线必过圆心
8.
7.
如图,在半径为 5 cm的⊙O中,直线 1 交⊙O于A、B两点,且弦AB =8 cm,要使直线 1 与⊙O相切,则需要将直线l平移( )
A.1cm或9cm B.2cm或8cm
C.2cm D.3cm
B
C
小试牛刀
如图,AB是⊙O的直径,AE平分∠BAF交⊙O交于E,过E点作直线与AF垂直,交AF延长线于D点,且交AB的延长线于C点.
(1)求证:CD是⊙O的切线;
9.
证明:连接OE, 则∠OAE=∠OEA.
由∠OAE=∠EAD ,得∠OEA=∠EAD,
所以OE∥AD.
因为AD⊥CD, 所以OE⊥CD,
所以CD是⊙O的切线.
小试牛刀
如图,AB是⊙O的直径,AE平分∠BAF交⊙O交于E,过E点作直线与AF垂直,交AF延长线于D点,且交AB的延长线于C点.
(2)若∠C=30°,DE= ,求⊙O的直径.
9.
解:过点O作OG⊥AD于点G.则∠AOG=∠ACD=30°,
四边形OEDG为矩形.
∴OG=ED=.
∴OA=2, ∴⊙O的直径是4.
课堂小结
课堂小结
1.直线和圆的位置关系:相交、相切、相离.
(1)从公共点数来判断;
(2)从d与r间的数量关系来判断.
2.直线和圆的位置关系的性质与判定:
(1)直线和圆相离 d>r;
(2)直线和圆相切 d=r;
(3)直线和圆相交 d<r.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
