人教版(新)九上-25.2 用列举法求概率 第二课时【优质课件】
文档属性
| 名称 | 人教版(新)九上-25.2 用列举法求概率 第二课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 14:08:09 | ||
图片预览








文档简介
(共29张PPT)
25.2 用列举法求概率
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
知道这个故事吗?给同学讲一下,并回答下列问题.
情景导入
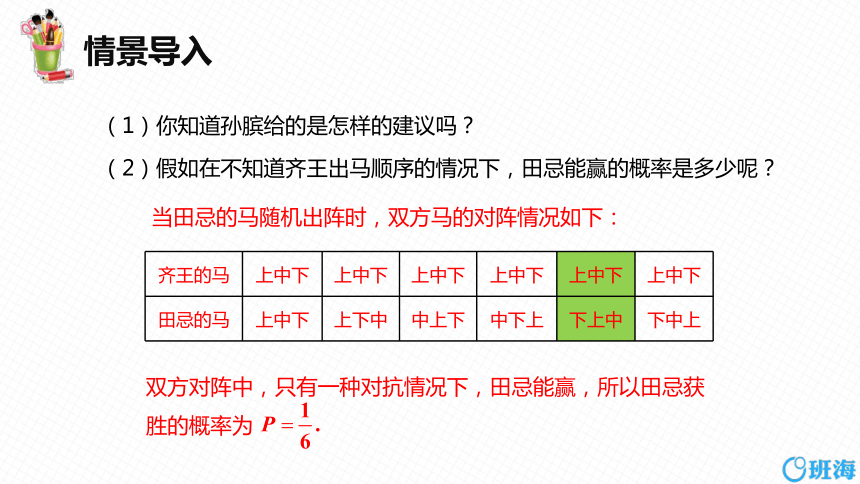
双方对阵中,只有一种对抗情况下,田忌能赢,所以田忌获胜的概率为
(1)你知道孙膑给的是怎样的建议吗?
(2)假如在不知道齐王出马顺序的情况下,田忌能赢的概率是多少呢?
当田忌的马随机出阵时,双方马的对阵情况如下:
齐王的马 上中下 上中下 上中下 上中下 上中下 上中下
田忌的马 上中下 上下中 中上下 中下上 下上中 下中上
新课精讲
探索新知
1
知识点
两步试验的树状图
这是上节课学习的列举法中的列表法,这节课学习列举法中的另一种方法——树状图法.
探索新知
解:如图,用画“树状图”法求概率.
例1 一个袋中有4个珠子,其中2个红色,2个蓝色,除颜色外其余特征均相同,若从这个袋中任取2个珠子,求都是蓝色珠子的概率.
∴P(都是蓝色珠子)=
可看出任取两个珠子共有12种等可能结果,其中都是蓝色珠子的有两种结果,
从中任取2个珠子可看作第一次取出一个,第二次再取出一个.
探索新知
总 结
用树状图法求概率的“四个步骤”:
1.定:确定该试验的几个步骤、顺序、每一步可能产生的结果.
2.画:列举每一环节可能产生的结果,得到树状图.
3.数:数出全部均等的结果数m和该事件出现的结果数n.
4.算:代入公式P(A)= .
典题精讲
1.一个布袋内只装有1个黑球和2个白球,这些球除颜色外其余都相同,随机摸出一个球后放回并搅匀,再随机摸出一个球,则两次摸出的球都是黑球的概率是( )
A. B. C. D.
D
典题精讲
2.同时拋掷两枚质地均匀的硬币,则下列事件发生的概率最大的是( )
A.两正面都朝上
B.两背面都朝上
C.一个正面朝上,另一个背面朝上
D.三种情况发生的概率一样大
D
探索新知
2
知识点
两步以上试验的树状图
例2 甲口袋中有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C,D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I.从三个口袋中各随机取出1个小球.
(1)取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少?
(2)取出的3个小球上全是辅音字母的概率是多少?
分析:当一次试验是从三个口袋中取球时,列表法就不方便了,为不重不漏地列出所有可能的结果,通常采用画树状图法.
探索新知
解:根据题意,可以画出如下的树状图:
探索新知
(1)只有1个元音字母的结果有5种,即ACH,ADH,BCI,BDI,
BEH,所以P(1个元音)=
由树状图可以看出,所有可能出现的结果共有12中,即
A A A A A A B B B B B B
C C D D E E C C D D E E
H I H I H I H I H I H I
这些结果出现的可能性相等.
探索新知
有2个元音字母的结果有4种,即ACI,ADI,AEH,BEI,所以P(2个元音)=
全部为元音字母的结果只有1种,即AEI,所以P(3个元音)=
(2)全是辅音字母的结果共有2种,即BCH,BDH,所以P(3个辅音)=
探索新知
总 结
(1)当事件涉及三个或三个以上元素时,用列表法不易列举出所有可能结果,用树状图可以依次列出所有可能的结果,求出n,再分别求出某个事件中包含的所有可能的结果,求出m,从而求出概率.
(2)用树状图法列举时,应注意取出后放回与不放回的问题.
典题精讲
1.有三个筹码,第一个一面画×,一面画○;第二个一面画○,一面画□;第三个一面画×,一面画□,依次抛掷这三个筹码,出现一对相同画面的概率是( )
A. B. C. D.
B
典题精讲
2.如图,一个小球从A点入口往下落,在每个交叉口都有向左或向右两种可能,且两种可能性相等.则小球最终从E点落出的概率为( )
A. B.
C. D.
C
学以致用
小试牛刀
1.掷一枚质地均匀的硬币两次,可能出现的结果有四种,我们可以利用如图所示的树状图来分析所有可能出现的结果,那么掷一枚硬币两次,至少有一次出现正面的概率是________.
2.同时抛掷三枚质地均匀的硬币,至少有两枚硬币正面向上的概率是( )
A. B. C. D.
D
小试牛刀
3.同时掷两枚质地均匀的硬币一次,两枚硬币都是正面朝上的概率是( )
A.1 B. C. D.
D
4.一个布袋里装有4个只有颜色不同的球,其中3个红球,1个白球,从布袋里摸出1个球,记下颜色后放回,搅匀,再摸出1个球,则两次摸到的球都是红球的概率是( )
A. B. C. D.
D
小试牛刀
5.在排球训练中,甲 乙 丙三人相互传球,由甲开始发球(记为第一次传球),则经过三次传球后,球仍回到甲手中的概率是( )
A. B. C. D.
B
6.小红 小明 小芳在一起做游戏时,需要确定游戏的先后顺序.他们约定用“石头 剪刀 布”的方式确定.问在一个回合中三个人都出“布”的概率是( )
A. B. C. D.
D
小试牛刀
7.甲 乙两人用如图所示的两个转盘(每个转盘被分成面积相等的3个扇形)做游戏,游戏规则:转动两个转盘各一次,当转盘停止后,指针所在区域的数字之和为偶数时甲获胜;数字之和为奇数时乙获胜.若指针落在分界线上,则需要重新转动转盘.甲获胜的概率是( )
A. B.
C. D.
C
小试牛刀
8.端午节当天,小明带了四个粽子(除味道不同外,其他均相同),其中两个是大枣味的,另外两个是火腿味的,准备按数量平均分给小红和小刚两个好朋友.
(1) 请你用画树状图的方法表示小红拿到的两个粽子的所有可能性.
解:(1)记两个大枣味的粽子分别为A1,A2,两个火腿味的粽子分别为B1,B2.
画树状图如图所示.
小试牛刀
(2)请你计算小红拿到的两个粽子刚好是同一味道的概率.
(2)由(1)可知,一共有12种等可能的结果,小红拿到的两个粽子刚好是同一味道的有4种结果,所以小红拿到的两个粽子刚好是同一味道的概率为
小试牛刀
9.体育课上,小明 小强 小华三人在踢足球,足球从一人传到
另一人就记为踢一次.
如果从小强开始踢,经过两次踢球后,足球踢到小华处的概
率是多少(用树状图表示)
如图:
由树状图易知P(两次后,
足球踢到小华处)= .
课堂小结
课堂小结
利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果;从而较方便地求出某些事件发生的概率.当试验包含两步时,列表法比较方便,当然,此时也可以用树状图法,当试验在三步或三步以上时,用树状图法方便.
通过本课时的学习,需要我们掌握:
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
25.2 用列举法求概率
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
知道这个故事吗?给同学讲一下,并回答下列问题.
情景导入
双方对阵中,只有一种对抗情况下,田忌能赢,所以田忌获胜的概率为
(1)你知道孙膑给的是怎样的建议吗?
(2)假如在不知道齐王出马顺序的情况下,田忌能赢的概率是多少呢?
当田忌的马随机出阵时,双方马的对阵情况如下:
齐王的马 上中下 上中下 上中下 上中下 上中下 上中下
田忌的马 上中下 上下中 中上下 中下上 下上中 下中上
新课精讲
探索新知
1
知识点
两步试验的树状图
这是上节课学习的列举法中的列表法,这节课学习列举法中的另一种方法——树状图法.
探索新知
解:如图,用画“树状图”法求概率.
例1 一个袋中有4个珠子,其中2个红色,2个蓝色,除颜色外其余特征均相同,若从这个袋中任取2个珠子,求都是蓝色珠子的概率.
∴P(都是蓝色珠子)=
可看出任取两个珠子共有12种等可能结果,其中都是蓝色珠子的有两种结果,
从中任取2个珠子可看作第一次取出一个,第二次再取出一个.
探索新知
总 结
用树状图法求概率的“四个步骤”:
1.定:确定该试验的几个步骤、顺序、每一步可能产生的结果.
2.画:列举每一环节可能产生的结果,得到树状图.
3.数:数出全部均等的结果数m和该事件出现的结果数n.
4.算:代入公式P(A)= .
典题精讲
1.一个布袋内只装有1个黑球和2个白球,这些球除颜色外其余都相同,随机摸出一个球后放回并搅匀,再随机摸出一个球,则两次摸出的球都是黑球的概率是( )
A. B. C. D.
D
典题精讲
2.同时拋掷两枚质地均匀的硬币,则下列事件发生的概率最大的是( )
A.两正面都朝上
B.两背面都朝上
C.一个正面朝上,另一个背面朝上
D.三种情况发生的概率一样大
D
探索新知
2
知识点
两步以上试验的树状图
例2 甲口袋中有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C,D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I.从三个口袋中各随机取出1个小球.
(1)取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少?
(2)取出的3个小球上全是辅音字母的概率是多少?
分析:当一次试验是从三个口袋中取球时,列表法就不方便了,为不重不漏地列出所有可能的结果,通常采用画树状图法.
探索新知
解:根据题意,可以画出如下的树状图:
探索新知
(1)只有1个元音字母的结果有5种,即ACH,ADH,BCI,BDI,
BEH,所以P(1个元音)=
由树状图可以看出,所有可能出现的结果共有12中,即
A A A A A A B B B B B B
C C D D E E C C D D E E
H I H I H I H I H I H I
这些结果出现的可能性相等.
探索新知
有2个元音字母的结果有4种,即ACI,ADI,AEH,BEI,所以P(2个元音)=
全部为元音字母的结果只有1种,即AEI,所以P(3个元音)=
(2)全是辅音字母的结果共有2种,即BCH,BDH,所以P(3个辅音)=
探索新知
总 结
(1)当事件涉及三个或三个以上元素时,用列表法不易列举出所有可能结果,用树状图可以依次列出所有可能的结果,求出n,再分别求出某个事件中包含的所有可能的结果,求出m,从而求出概率.
(2)用树状图法列举时,应注意取出后放回与不放回的问题.
典题精讲
1.有三个筹码,第一个一面画×,一面画○;第二个一面画○,一面画□;第三个一面画×,一面画□,依次抛掷这三个筹码,出现一对相同画面的概率是( )
A. B. C. D.
B
典题精讲
2.如图,一个小球从A点入口往下落,在每个交叉口都有向左或向右两种可能,且两种可能性相等.则小球最终从E点落出的概率为( )
A. B.
C. D.
C
学以致用
小试牛刀
1.掷一枚质地均匀的硬币两次,可能出现的结果有四种,我们可以利用如图所示的树状图来分析所有可能出现的结果,那么掷一枚硬币两次,至少有一次出现正面的概率是________.
2.同时抛掷三枚质地均匀的硬币,至少有两枚硬币正面向上的概率是( )
A. B. C. D.
D
小试牛刀
3.同时掷两枚质地均匀的硬币一次,两枚硬币都是正面朝上的概率是( )
A.1 B. C. D.
D
4.一个布袋里装有4个只有颜色不同的球,其中3个红球,1个白球,从布袋里摸出1个球,记下颜色后放回,搅匀,再摸出1个球,则两次摸到的球都是红球的概率是( )
A. B. C. D.
D
小试牛刀
5.在排球训练中,甲 乙 丙三人相互传球,由甲开始发球(记为第一次传球),则经过三次传球后,球仍回到甲手中的概率是( )
A. B. C. D.
B
6.小红 小明 小芳在一起做游戏时,需要确定游戏的先后顺序.他们约定用“石头 剪刀 布”的方式确定.问在一个回合中三个人都出“布”的概率是( )
A. B. C. D.
D
小试牛刀
7.甲 乙两人用如图所示的两个转盘(每个转盘被分成面积相等的3个扇形)做游戏,游戏规则:转动两个转盘各一次,当转盘停止后,指针所在区域的数字之和为偶数时甲获胜;数字之和为奇数时乙获胜.若指针落在分界线上,则需要重新转动转盘.甲获胜的概率是( )
A. B.
C. D.
C
小试牛刀
8.端午节当天,小明带了四个粽子(除味道不同外,其他均相同),其中两个是大枣味的,另外两个是火腿味的,准备按数量平均分给小红和小刚两个好朋友.
(1) 请你用画树状图的方法表示小红拿到的两个粽子的所有可能性.
解:(1)记两个大枣味的粽子分别为A1,A2,两个火腿味的粽子分别为B1,B2.
画树状图如图所示.
小试牛刀
(2)请你计算小红拿到的两个粽子刚好是同一味道的概率.
(2)由(1)可知,一共有12种等可能的结果,小红拿到的两个粽子刚好是同一味道的有4种结果,所以小红拿到的两个粽子刚好是同一味道的概率为
小试牛刀
9.体育课上,小明 小强 小华三人在踢足球,足球从一人传到
另一人就记为踢一次.
如果从小强开始踢,经过两次踢球后,足球踢到小华处的概
率是多少(用树状图表示)
如图:
由树状图易知P(两次后,
足球踢到小华处)= .
课堂小结
课堂小结
利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果;从而较方便地求出某些事件发生的概率.当试验包含两步时,列表法比较方便,当然,此时也可以用树状图法,当试验在三步或三步以上时,用树状图法方便.
通过本课时的学习,需要我们掌握:
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
