人教版(新)九上-25.2 用列举法求概率 第一课时【优质课件】
文档属性
| 名称 | 人教版(新)九上-25.2 用列举法求概率 第一课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 14:08:09 | ||
图片预览











文档简介
(共31张PPT)
25.2 用列举法求概率
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
在一次试验中,如果可能出现的结果只有有限个,且各种结果出现的可能性大小相等,那么我们可以通过列举试验结果的方法,求出随机事件发生的概率.
新课精讲
探索新知
1
知识点
用枚举法求概率(等可能事件结果有限个)
用枚举法求某一事件的概率,关键是找出所有可
能发生的结果以及某一事件发生的结果.
探索新知
解:列举抛掷两枚硬币所能产生的全部结果,它们是:正正,正反,反正,反反.
所有可能的结果共有4种,并且这4种结果出现的可能性相等.
例1 同时抛掷两枚质地均匀的硬币,求下列事件的概率:
(1)两枚硬币全部正面向上;
(2)两枚硬币全部反面向上;
(3)一枚硬币正面向上、一枚硬币反面向上.
探索新知
(2)两枚硬币全部反面向上(记为事件B) 的结果也只有1种,即“反反”,所以
(1)所有可能的结果中,满足两枚硬币全部正面向上 (记为事件A) 的结果只有1种,即“正正”, 所以
(3)一枚硬币正面向上、一枚硬币反面向上(记为事件C) 的结果共有2种,即“反正”“正反”,所以
探索新知
总 结
直接列举法求概率的采用:当试验的结果是有限个的,且这些结果出现的可能性相等,并决定这些概率的因素只有一个时采用.
探索新知
思考
“同时抛掷两枚质地均匀的硬币”与“先后两次抛掷一枚质地均匀的硬币”,这两种试验的所有可能结果一样吗?
典题精讲
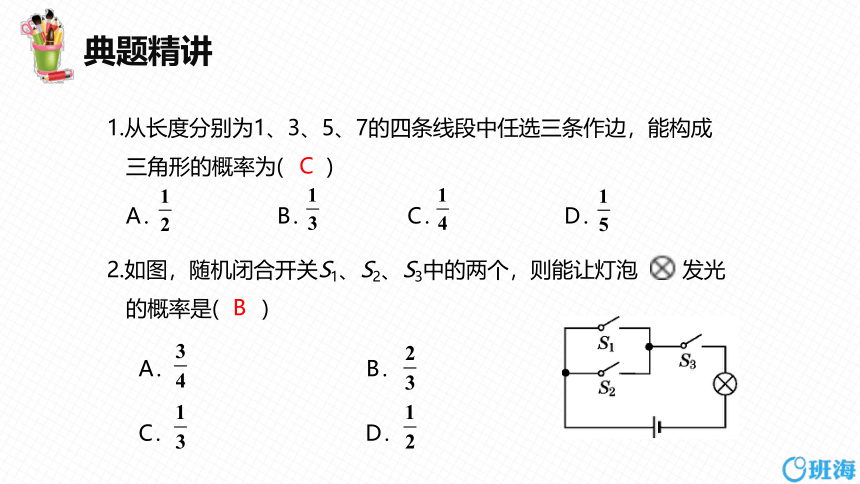
2.如图,随机闭合开关S1、S2、S3中的两个,则能让灯泡 发光
的概率是( )
A. B.
C. D.
1.从长度分别为1、3、5、7的四条线段中任选三条作边,能构成
三角形的概率为( )
A. B. C. D.
C
B
探索新知
2
知识点
用列表法求概率(等可能事件结果较多个)
对于求两步以上的概率采用列表法.
探索新知
例2 同时掷两枚质地均匀的骰子,计算下列事件的概率:
(1)两枚骰子的点数相同;
(2)两枚骰子点数的和是9;
(3)至少有一枚骰子的点数为2.
分析:当一次试验是掷两枚骰子时,为不重不漏地列出所有可能的结果,通常采用列表法.
探索新知
解:两枚骰子分别记为第1枚和第2枚,可以用下表列举出所有可能出现的结果.
1 2 3 4 5 6
1 (1,1) (2,1) (3,1) (4,1) (5,1) (6,1)
2 (1,2) (2,2) (3,2) (4,2) (5,2) (6,2)
3 (1,3) (2,3) (3,3) (4,3) (5,3) (6,3)
4 (1,4) (2,4) (3,4) (4,4) (5,4) (6,4)
5 (1,5) (2,5) (3,5) (4,5) (5,5) (6,5)
6 (1,6) (2,6) (3,6) (4,6) (5,6) (6,6)
第1枚
第2枚
探索新知
(1)两枚骰子的点数相同(记为事件A)的结果有6种,
即(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),
所以
由上表可以看出,同时掷两枚骰子,可能出现的结果有36种,并且它们出现的可能性相同.
(2)两枚骰子的点数和是9(记为事件B)的结果有4种,
即(3,6),(4,5),(5,4),(6,3),所以
探索新知
(3)至少有一枚骰子的点数为2(记为事件C)的结果
有11种,即(1,2),(2,1),(2,2),(2,3),(2,4),
(2,5),(2,6),(3,2),(4,2),(5,2),(6,2),
所以
探索新知
2.适用条件:如果事件中各种结果出现的可能性均等,含有两次操作(如掷骰子两次)或两个条件(如两个转盘)的事件.
总 结
1.用列表法求概率的步骤:①列表;②通过表格计数,确定所有 等可能的结果数n和关注的结果数m的值;③利用概率公式
计算出事件的概率.
探索新知
思考
如果把例2中的“同时掷两枚质地均匀的骰子”改为“把一枚质地均匀的骰子掷两次”,得到的结果有变化吗?为什么
典题精讲
小强和小华两人玩“剪刀、石头、布”游戏,随机出手一次,则两人平局的概率为( )
A.
B.
C.
D.
B
学以致用
小试牛刀
1.在一次试验中,若可能出现的结果只有______个,且各种结果出现的可能性大小________,可用列举试验结果的方法,求出随机事件发生的概率.
有限
相等
2.列表法求概率:当一次试验涉及____个因素,并且可能出现的结果数目较____时,为不重不漏地列出所有可能结果,通常采用列表法.
两
多
小试牛刀
3.小明和小华参加社会实践活动,随机选择“打扫社区卫生”和“参加社会调查”其中一项,那么两人同时选择“参加社会调查”的概率为( )
A. B. C. D.
A
4.小明和小华玩“石头 剪刀 布”的游戏,若随机出手一次,则小华获胜的概率是( )
A. B. C. D.
C
小试牛刀
5.在一个不透明的袋子里装有四个小球,球上分别标有6,7,8,9四个数字,这些小球除数字外都相同.甲 乙两人玩“猜数字”游戏,甲先从袋中任意摸出一个小球,将小球上的数字记为m,再由乙猜这个小球上的数字,记为n.如果m,n满足|m-n|≤1,那么就称甲 乙两人“心领神会”,则两人“心领神会”的概率是( )
A. B. C. D.
B
小试牛刀
6.如图,随机闭合开关S1,S2,S3中的两个,则
能让灯泡发光的概率是( )
A. B. C. D.
B
7.某校高一年级今年计划招四个班的新生,并采取随机摇号的方法分班,小明和小红既是该校的高一新生,又是好朋友,那么小明和小红分在同一个班的机会是( )
A. B. C. D.
A
小试牛刀
8.已知一次函数y=kx+b,k从2,-3中随机取一个值,b从1,-1,-2中随机取一个值,则该一次函数的图象经过第二 三 四象限的概率为( )
A. B. C. D.
A
9.有6张看上去无差别的卡片,上面分别写着1,2,3,4,5,6,随机抽取一张后,放回并混在一起,再随机抽取一张,两次抽取的数字的积为奇数的概率是( )
A. B. C. D.
B
小试牛刀
10.在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲 乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
(1)请用列表或画树状图的方法表示出上述游戏
中两数和的所有可能的结果;
小试牛刀
解:(1)根据题意列表如下:
乙和甲 6 7 8 9
3 9 10 11 12
4 10 11 12 13
5 11 12 13 14
小试牛刀
(2)由(1)可知,两数和共有12种等可能的情况,其中和小于12的情况有6种,和大于12的情况有3种,
∴李燕获胜的概率为 ,
刘凯获胜的概率为
课堂小结
课堂小结
1.直接列举法求概率的采用:当试验的结果是有限个的,且这些结果出现的可能性相等,并决定这些概率的因素只有一个时采用.
3.适用条件:如果事件中各种结果出现的可能性均等,含有两次操作(如掷骰子两次)或两个条件(如两个转盘)的事件.
2.用列表法求概率的步骤:①列表;②通过表格计数,确定所有 等可能的结果数n和关注的结果数m的值;③利用概率公式
计算出事件的概率.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
25.2 用列举法求概率
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
在一次试验中,如果可能出现的结果只有有限个,且各种结果出现的可能性大小相等,那么我们可以通过列举试验结果的方法,求出随机事件发生的概率.
新课精讲
探索新知
1
知识点
用枚举法求概率(等可能事件结果有限个)
用枚举法求某一事件的概率,关键是找出所有可
能发生的结果以及某一事件发生的结果.
探索新知
解:列举抛掷两枚硬币所能产生的全部结果,它们是:正正,正反,反正,反反.
所有可能的结果共有4种,并且这4种结果出现的可能性相等.
例1 同时抛掷两枚质地均匀的硬币,求下列事件的概率:
(1)两枚硬币全部正面向上;
(2)两枚硬币全部反面向上;
(3)一枚硬币正面向上、一枚硬币反面向上.
探索新知
(2)两枚硬币全部反面向上(记为事件B) 的结果也只有1种,即“反反”,所以
(1)所有可能的结果中,满足两枚硬币全部正面向上 (记为事件A) 的结果只有1种,即“正正”, 所以
(3)一枚硬币正面向上、一枚硬币反面向上(记为事件C) 的结果共有2种,即“反正”“正反”,所以
探索新知
总 结
直接列举法求概率的采用:当试验的结果是有限个的,且这些结果出现的可能性相等,并决定这些概率的因素只有一个时采用.
探索新知
思考
“同时抛掷两枚质地均匀的硬币”与“先后两次抛掷一枚质地均匀的硬币”,这两种试验的所有可能结果一样吗?
典题精讲
2.如图,随机闭合开关S1、S2、S3中的两个,则能让灯泡 发光
的概率是( )
A. B.
C. D.
1.从长度分别为1、3、5、7的四条线段中任选三条作边,能构成
三角形的概率为( )
A. B. C. D.
C
B
探索新知
2
知识点
用列表法求概率(等可能事件结果较多个)
对于求两步以上的概率采用列表法.
探索新知
例2 同时掷两枚质地均匀的骰子,计算下列事件的概率:
(1)两枚骰子的点数相同;
(2)两枚骰子点数的和是9;
(3)至少有一枚骰子的点数为2.
分析:当一次试验是掷两枚骰子时,为不重不漏地列出所有可能的结果,通常采用列表法.
探索新知
解:两枚骰子分别记为第1枚和第2枚,可以用下表列举出所有可能出现的结果.
1 2 3 4 5 6
1 (1,1) (2,1) (3,1) (4,1) (5,1) (6,1)
2 (1,2) (2,2) (3,2) (4,2) (5,2) (6,2)
3 (1,3) (2,3) (3,3) (4,3) (5,3) (6,3)
4 (1,4) (2,4) (3,4) (4,4) (5,4) (6,4)
5 (1,5) (2,5) (3,5) (4,5) (5,5) (6,5)
6 (1,6) (2,6) (3,6) (4,6) (5,6) (6,6)
第1枚
第2枚
探索新知
(1)两枚骰子的点数相同(记为事件A)的结果有6种,
即(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),
所以
由上表可以看出,同时掷两枚骰子,可能出现的结果有36种,并且它们出现的可能性相同.
(2)两枚骰子的点数和是9(记为事件B)的结果有4种,
即(3,6),(4,5),(5,4),(6,3),所以
探索新知
(3)至少有一枚骰子的点数为2(记为事件C)的结果
有11种,即(1,2),(2,1),(2,2),(2,3),(2,4),
(2,5),(2,6),(3,2),(4,2),(5,2),(6,2),
所以
探索新知
2.适用条件:如果事件中各种结果出现的可能性均等,含有两次操作(如掷骰子两次)或两个条件(如两个转盘)的事件.
总 结
1.用列表法求概率的步骤:①列表;②通过表格计数,确定所有 等可能的结果数n和关注的结果数m的值;③利用概率公式
计算出事件的概率.
探索新知
思考
如果把例2中的“同时掷两枚质地均匀的骰子”改为“把一枚质地均匀的骰子掷两次”,得到的结果有变化吗?为什么
典题精讲
小强和小华两人玩“剪刀、石头、布”游戏,随机出手一次,则两人平局的概率为( )
A.
B.
C.
D.
B
学以致用
小试牛刀
1.在一次试验中,若可能出现的结果只有______个,且各种结果出现的可能性大小________,可用列举试验结果的方法,求出随机事件发生的概率.
有限
相等
2.列表法求概率:当一次试验涉及____个因素,并且可能出现的结果数目较____时,为不重不漏地列出所有可能结果,通常采用列表法.
两
多
小试牛刀
3.小明和小华参加社会实践活动,随机选择“打扫社区卫生”和“参加社会调查”其中一项,那么两人同时选择“参加社会调查”的概率为( )
A. B. C. D.
A
4.小明和小华玩“石头 剪刀 布”的游戏,若随机出手一次,则小华获胜的概率是( )
A. B. C. D.
C
小试牛刀
5.在一个不透明的袋子里装有四个小球,球上分别标有6,7,8,9四个数字,这些小球除数字外都相同.甲 乙两人玩“猜数字”游戏,甲先从袋中任意摸出一个小球,将小球上的数字记为m,再由乙猜这个小球上的数字,记为n.如果m,n满足|m-n|≤1,那么就称甲 乙两人“心领神会”,则两人“心领神会”的概率是( )
A. B. C. D.
B
小试牛刀
6.如图,随机闭合开关S1,S2,S3中的两个,则
能让灯泡发光的概率是( )
A. B. C. D.
B
7.某校高一年级今年计划招四个班的新生,并采取随机摇号的方法分班,小明和小红既是该校的高一新生,又是好朋友,那么小明和小红分在同一个班的机会是( )
A. B. C. D.
A
小试牛刀
8.已知一次函数y=kx+b,k从2,-3中随机取一个值,b从1,-1,-2中随机取一个值,则该一次函数的图象经过第二 三 四象限的概率为( )
A. B. C. D.
A
9.有6张看上去无差别的卡片,上面分别写着1,2,3,4,5,6,随机抽取一张后,放回并混在一起,再随机抽取一张,两次抽取的数字的积为奇数的概率是( )
A. B. C. D.
B
小试牛刀
10.在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲 乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
(1)请用列表或画树状图的方法表示出上述游戏
中两数和的所有可能的结果;
小试牛刀
解:(1)根据题意列表如下:
乙和甲 6 7 8 9
3 9 10 11 12
4 10 11 12 13
5 11 12 13 14
小试牛刀
(2)由(1)可知,两数和共有12种等可能的情况,其中和小于12的情况有6种,和大于12的情况有3种,
∴李燕获胜的概率为 ,
刘凯获胜的概率为
课堂小结
课堂小结
1.直接列举法求概率的采用:当试验的结果是有限个的,且这些结果出现的可能性相等,并决定这些概率的因素只有一个时采用.
3.适用条件:如果事件中各种结果出现的可能性均等,含有两次操作(如掷骰子两次)或两个条件(如两个转盘)的事件.
2.用列表法求概率的步骤:①列表;②通过表格计数,确定所有 等可能的结果数n和关注的结果数m的值;③利用概率公式
计算出事件的概率.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
