人教版(新)七上-24.1.4 圆周角数 第一课时【优质课件】
文档属性
| 名称 | 人教版(新)七上-24.1.4 圆周角数 第一课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览








文档简介
(共31张PPT)
24.1.4 圆周角
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
回顾旧知
什么是圆心角?它具有哪些性质?
新课精讲
探索新知
1
知识点
圆周角的定义
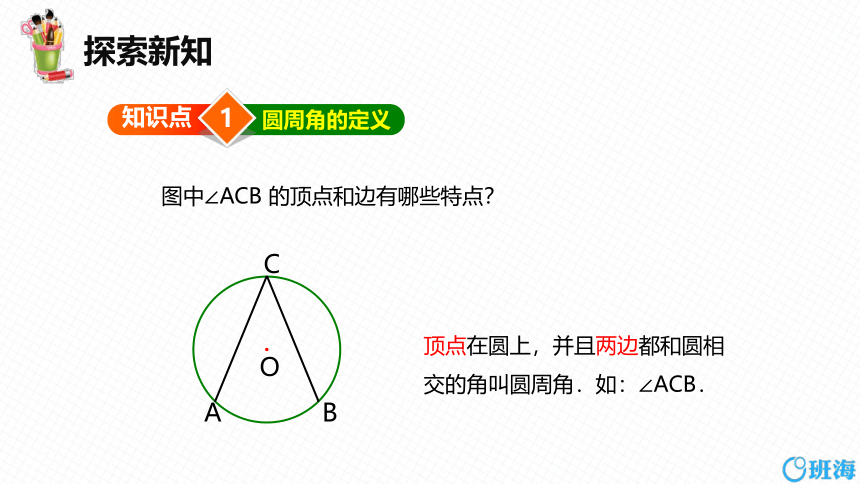
图中∠ACB 的顶点和边有哪些特点?
A
O
B
C
顶点在圆上,并且两边都和圆相交的角叫圆周角.如:∠ACB.
探索新知
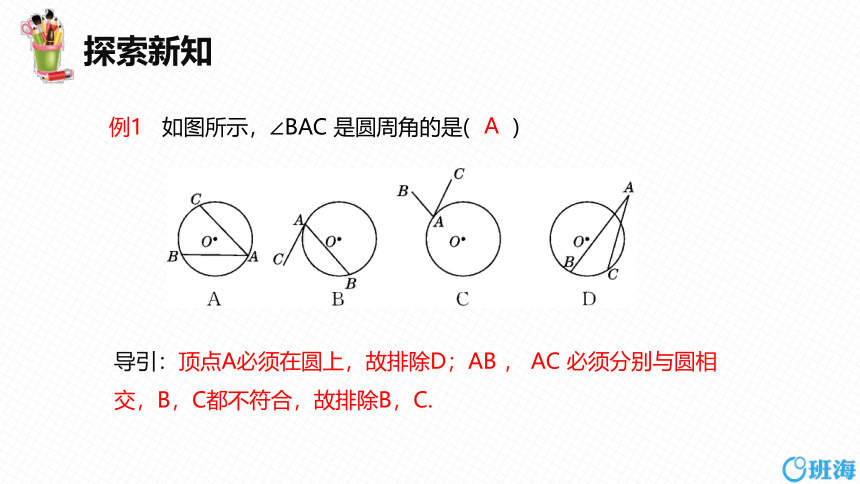
例1 如图所示,∠BAC 是圆周角的是( )
导引:顶点A必须在圆上,故排除D;AB , AC 必须分别与圆相交,B,C都不符合,故排除B,C.
A
探索新知
总 结
解答本例运用了定义法和排除法.要判断一个角是不是圆周角,必须抓住圆周角定义中的两个特征:①角的顶点在圆上,②角的两边都与圆相交,①与②缺一不可.
典题精讲
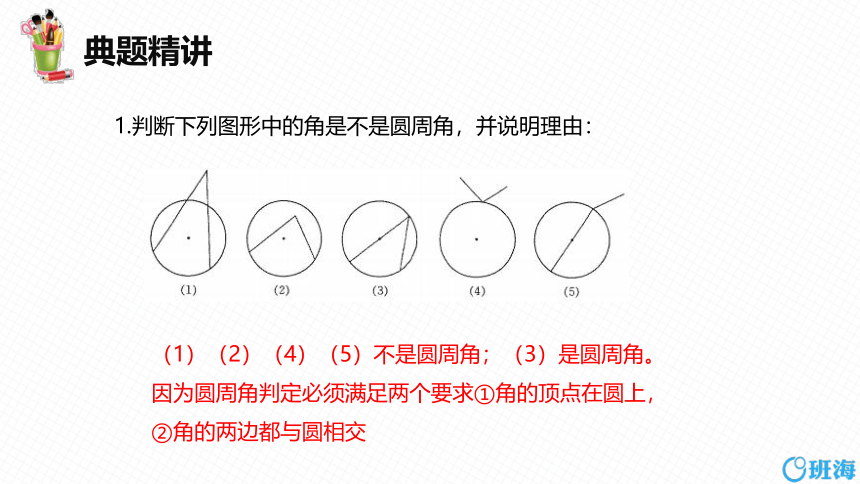
1.判断下列图形中的角是不是圆周角,并说明理由:
(1)(2)(4)(5)不是圆周角;(3)是圆周角。因为圆周角判定必须满足两个要求①角的顶点在圆上,②角的两边都与圆相交
典题精讲
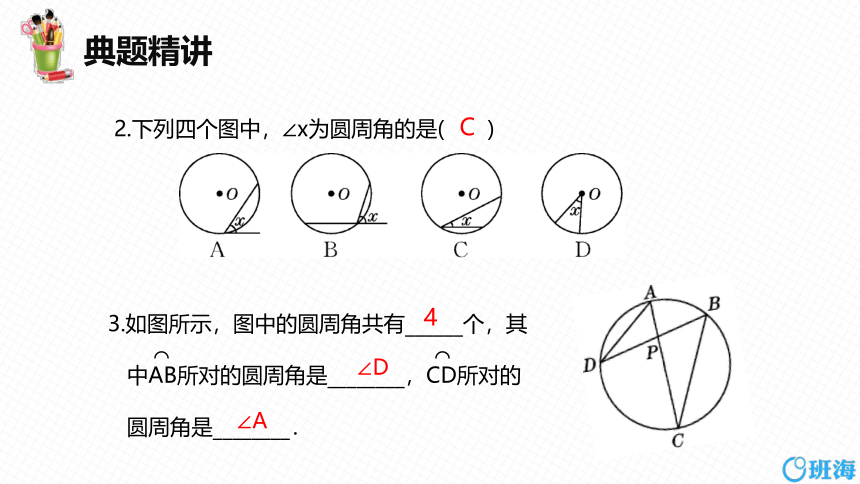
2.下列四个图中,∠x为圆周角的是( )
C
3.如图所示,图中的圆周角共有______个,其
中AB所对的圆周角是________,CD所对的
圆周角是________.
⌒
⌒
4
∠D
∠A
探索新知
2
知识点
圆周角与圆心角的关系
刚刚认识了什么是圆周角,在图中既有圆心角,又有圆周角,并且还可以发现∠ACB与∠AOB对着同一条弧AB,它们之间存在什么关系呢?下面我们就来研究这个问题.
⌒
问 题
探索新知
探究:分别测量图中AB所对的圆周角∠ACB和圆心角∠AOB的度数,它们之间有什么关系?
在⊙O上任取一条弧,作出这条弧所对的圆周角和圆心角,测量它们的度数,你能得出同样的结论吗?由此你能发现什么规律?
⌒
探索新知
归 纳
我们可以发现,同弧所对的圆周角的度数等于这条弧所对的圆心角的度数的一半,即:∠ACB= ∠AOB.
探索新知
例2 我们来证明一下上面的结论.
在圆上任取BC,画出圆心角∠BOC和圆周角∠BAC,圆心角和圆周角有下面几种位置关系.
⌒
我们来分析第(1)种情况,如图(1),圆心O在∠BAC的一条边上.
证明:
对于第(2)(3)种情况,可以通过添加辅助线(图(2)(3)),将它们转化为第(1)种情况.从而得到相同的结论(请你自己完成证明).
探索新知
总 结
一条弧所对的圆周角等于它所对的圆心角的一半.
典题精讲
1.将量角器按如图所示的方式放置在三角形纸板上,使顶点C在
半圆上,点A,B的读数分别为100°,150°,则∠ACB的大小
为________度.
28
典题精讲
2.如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,
∠B=30°,则∠ADC的度数为________.
110°
探索新知
3
知识点
同弧或等弧与所对圆周角的关系
思考:
一条弧所对的圆周角之间有什么关系?同弧或等弧所对的圆周角之间有什么关系?
同弧或等弧所对的圆周角相等.
A
D
B
C
O
探索新知
例3 如图,在⊙O中, ,∠BAC=50°,则∠AEC的度数为( )
A.65° B.75° C.50° D.55°
导引:由 ,可知∠ABC=∠ACB,已知∠BAC=50°,故根据三角形内角和定理,可求出∠ABC的度数,再根据“同弧所对的圆周角相等”,可得结果.
∵ ,∴∠ABC=∠ACB.
∵∠BAC=50°,∴∠ABC= ×(180°-50°) =65°.
∴∠AEC=∠ABC=65°,故选A.
A
探索新知
在一个圆中求一个圆周角的度数,可以从三个方面转化:
(1)转化为求该圆周角所对的弧所对的圆心角的度数;
(2)转化为求该圆周角所对的弧所对的其他圆周角的度数;
(3)转化为求与该圆周角所对的弧相等的弧所对的圆心角或圆周角的度数.
总 结
典题精讲
1.如图,将⊙O沿弦AB折叠,圆弧恰好经过圆心O,点P是 上一
点,则∠APB的度数为( )
A.45°
B.30°
C.75°
D.60°
D
典题精讲
2.如图,在⊙O中,弦AB与CD交于点M,∠A=45°,∠AMD=75°,
则∠B的度数是( )
A.15° B.25°
C.30° D.75°
3.如图,在⊙O中, ,∠AOB=40°,
则∠ADC的度数是( )
A.40° B.30°
C.20° D.15°
C
C
学以致用
小试牛刀
1.顶点________,并且________分别与圆还有另一个交点的角叫做圆周角.
在圆上
两边
2.在⊙O中,A,B是圆上任意两点,则AB所对的圆心角有________个,
所对的圆周角有________ 个;弦AB所对的圆心角有______个,所对
的圆周角有______个.
1
无数
1
无数
3.在同圆或等圆中,________或________所对的圆周角相等;相等的圆
周角所对的弧________.
同弧
等弧
相等
小试牛刀
4.如图,⊙C经过原点,并与两坐标轴分别交于
A,D两点,已知∠OBA=30°,点A的坐标为
(2,0),则点D的坐标为__________.
(0,2)
5.圆周角定理:一条弧所对的圆周角等于它所对的圆心角的________.
一半
小试牛刀
6.如图,在⊙O中,AB是直径,AC是弦,连接OC,若∠ACO=30°,则∠BOC的度数是( )
A.30° B.45°
C.55° D.60°
D
7.如图,点A,B,C,P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为
D,E,∠DCE=40°,则∠P的度数为( )
A.140° B.70°
C.60° D.40°
B
小试牛刀
8.如图,在⊙O中,AB=BC,点D在⊙O上,∠CDB=25°,则∠AOB
=( )
A.45°
B.50°
C.55°
D.60°
B
小试牛刀
9.如图,在⊙O中,弦AB⊥弦CD于点E.
求证:∠BOC+∠AOD=180°.
连接AC,∵圆周角∠CAB与圆心角∠BOC同是所对的角,
∴∠BOC=2∠BAC.
∵圆周角∠ACD与圆心角∠AOD同是所对的角,∴∠AOD=2∠ACD.
∵AB⊥CD,∴∠AEC=90°.
证明:
在Rt△AEC中,∠BAC+∠ACD=90°,
∴∠BOC+∠AOD=2∠BAC+2∠ACD=2(∠BAC+∠ACD)=2×90°=180°.
课堂小结
课堂小结
内容小结:
(1)一个概念(圆周角);
(2)一个定理:一条弧所对的圆周角等于该弧所对的圆心角的一半;
(3)一个推论:同圆内,同弧或等弧所对的圆周角相等. 相等的圆周角所对的弧相等;
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
24.1.4 圆周角
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
回顾旧知
什么是圆心角?它具有哪些性质?
新课精讲
探索新知
1
知识点
圆周角的定义
图中∠ACB 的顶点和边有哪些特点?
A
O
B
C
顶点在圆上,并且两边都和圆相交的角叫圆周角.如:∠ACB.
探索新知
例1 如图所示,∠BAC 是圆周角的是( )
导引:顶点A必须在圆上,故排除D;AB , AC 必须分别与圆相交,B,C都不符合,故排除B,C.
A
探索新知
总 结
解答本例运用了定义法和排除法.要判断一个角是不是圆周角,必须抓住圆周角定义中的两个特征:①角的顶点在圆上,②角的两边都与圆相交,①与②缺一不可.
典题精讲
1.判断下列图形中的角是不是圆周角,并说明理由:
(1)(2)(4)(5)不是圆周角;(3)是圆周角。因为圆周角判定必须满足两个要求①角的顶点在圆上,②角的两边都与圆相交
典题精讲
2.下列四个图中,∠x为圆周角的是( )
C
3.如图所示,图中的圆周角共有______个,其
中AB所对的圆周角是________,CD所对的
圆周角是________.
⌒
⌒
4
∠D
∠A
探索新知
2
知识点
圆周角与圆心角的关系
刚刚认识了什么是圆周角,在图中既有圆心角,又有圆周角,并且还可以发现∠ACB与∠AOB对着同一条弧AB,它们之间存在什么关系呢?下面我们就来研究这个问题.
⌒
问 题
探索新知
探究:分别测量图中AB所对的圆周角∠ACB和圆心角∠AOB的度数,它们之间有什么关系?
在⊙O上任取一条弧,作出这条弧所对的圆周角和圆心角,测量它们的度数,你能得出同样的结论吗?由此你能发现什么规律?
⌒
探索新知
归 纳
我们可以发现,同弧所对的圆周角的度数等于这条弧所对的圆心角的度数的一半,即:∠ACB= ∠AOB.
探索新知
例2 我们来证明一下上面的结论.
在圆上任取BC,画出圆心角∠BOC和圆周角∠BAC,圆心角和圆周角有下面几种位置关系.
⌒
我们来分析第(1)种情况,如图(1),圆心O在∠BAC的一条边上.
证明:
对于第(2)(3)种情况,可以通过添加辅助线(图(2)(3)),将它们转化为第(1)种情况.从而得到相同的结论(请你自己完成证明).
探索新知
总 结
一条弧所对的圆周角等于它所对的圆心角的一半.
典题精讲
1.将量角器按如图所示的方式放置在三角形纸板上,使顶点C在
半圆上,点A,B的读数分别为100°,150°,则∠ACB的大小
为________度.
28
典题精讲
2.如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,
∠B=30°,则∠ADC的度数为________.
110°
探索新知
3
知识点
同弧或等弧与所对圆周角的关系
思考:
一条弧所对的圆周角之间有什么关系?同弧或等弧所对的圆周角之间有什么关系?
同弧或等弧所对的圆周角相等.
A
D
B
C
O
探索新知
例3 如图,在⊙O中, ,∠BAC=50°,则∠AEC的度数为( )
A.65° B.75° C.50° D.55°
导引:由 ,可知∠ABC=∠ACB,已知∠BAC=50°,故根据三角形内角和定理,可求出∠ABC的度数,再根据“同弧所对的圆周角相等”,可得结果.
∵ ,∴∠ABC=∠ACB.
∵∠BAC=50°,∴∠ABC= ×(180°-50°) =65°.
∴∠AEC=∠ABC=65°,故选A.
A
探索新知
在一个圆中求一个圆周角的度数,可以从三个方面转化:
(1)转化为求该圆周角所对的弧所对的圆心角的度数;
(2)转化为求该圆周角所对的弧所对的其他圆周角的度数;
(3)转化为求与该圆周角所对的弧相等的弧所对的圆心角或圆周角的度数.
总 结
典题精讲
1.如图,将⊙O沿弦AB折叠,圆弧恰好经过圆心O,点P是 上一
点,则∠APB的度数为( )
A.45°
B.30°
C.75°
D.60°
D
典题精讲
2.如图,在⊙O中,弦AB与CD交于点M,∠A=45°,∠AMD=75°,
则∠B的度数是( )
A.15° B.25°
C.30° D.75°
3.如图,在⊙O中, ,∠AOB=40°,
则∠ADC的度数是( )
A.40° B.30°
C.20° D.15°
C
C
学以致用
小试牛刀
1.顶点________,并且________分别与圆还有另一个交点的角叫做圆周角.
在圆上
两边
2.在⊙O中,A,B是圆上任意两点,则AB所对的圆心角有________个,
所对的圆周角有________ 个;弦AB所对的圆心角有______个,所对
的圆周角有______个.
1
无数
1
无数
3.在同圆或等圆中,________或________所对的圆周角相等;相等的圆
周角所对的弧________.
同弧
等弧
相等
小试牛刀
4.如图,⊙C经过原点,并与两坐标轴分别交于
A,D两点,已知∠OBA=30°,点A的坐标为
(2,0),则点D的坐标为__________.
(0,2)
5.圆周角定理:一条弧所对的圆周角等于它所对的圆心角的________.
一半
小试牛刀
6.如图,在⊙O中,AB是直径,AC是弦,连接OC,若∠ACO=30°,则∠BOC的度数是( )
A.30° B.45°
C.55° D.60°
D
7.如图,点A,B,C,P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为
D,E,∠DCE=40°,则∠P的度数为( )
A.140° B.70°
C.60° D.40°
B
小试牛刀
8.如图,在⊙O中,AB=BC,点D在⊙O上,∠CDB=25°,则∠AOB
=( )
A.45°
B.50°
C.55°
D.60°
B
小试牛刀
9.如图,在⊙O中,弦AB⊥弦CD于点E.
求证:∠BOC+∠AOD=180°.
连接AC,∵圆周角∠CAB与圆心角∠BOC同是所对的角,
∴∠BOC=2∠BAC.
∵圆周角∠ACD与圆心角∠AOD同是所对的角,∴∠AOD=2∠ACD.
∵AB⊥CD,∴∠AEC=90°.
证明:
在Rt△AEC中,∠BAC+∠ACD=90°,
∴∠BOC+∠AOD=2∠BAC+2∠ACD=2(∠BAC+∠ACD)=2×90°=180°.
课堂小结
课堂小结
内容小结:
(1)一个概念(圆周角);
(2)一个定理:一条弧所对的圆周角等于该弧所对的圆心角的一半;
(3)一个推论:同圆内,同弧或等弧所对的圆周角相等. 相等的圆周角所对的弧相等;
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
