人教版(新)九上-21.1 一元二次方程【优质课件】
文档属性
| 名称 | 人教版(新)九上-21.1 一元二次方程【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览










文档简介
(共43张PPT)
21.1 一元二次方程
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
判断下列式子是否是一元一次方程:
回顾旧知
一元一次方程
1、只有一个未知数
2、未知数的指数是一次
3、方程的两边都是整式
新课精讲
探索新知
1
知识点
一元二次方程的定义
问 题(一)
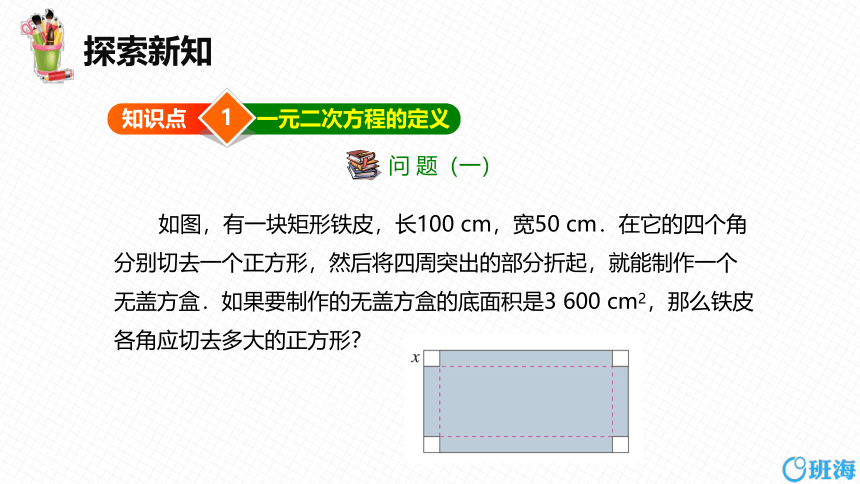
如图,有一块矩形铁皮,长100 cm,宽50 cm.在它的四个角分别切去一个正方形,然后将四周突出的部分折起,就能制作一个无盖方盒.如果要制作的无盖方盒的底面积是3 600 cm2,那么铁皮各角应切去多大的正方形?
探索新知
设切去的正方形的边长是x cm,则盒底的长为(100-2x)cm,宽为
(50-2x)cm.根据方盒的底面积为3600cm2,得
(100-2x)(50-2x)=3 600.
整理,得4x2-300x+1400=0
化简,得x2-75x+350=0
解上面方程即可得出所切正方形的具体尺寸.
化简后的方程中未知数的个数和最高次数各是多少?
探索新知
问 题(二)
要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场.根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应该邀请多少个队参赛?
全部比赛场数为 4×7=28.
设应邀请x个队参赛,每个队要与其他(x-1)个队各赛一场,因为甲队对乙队的比赛和乙队对甲队的比赛是同一场比赛,所以全部比赛共 场.
列方程
整理,得
化简,得x -x=56解方程即可得出参赛队数.
探索新知
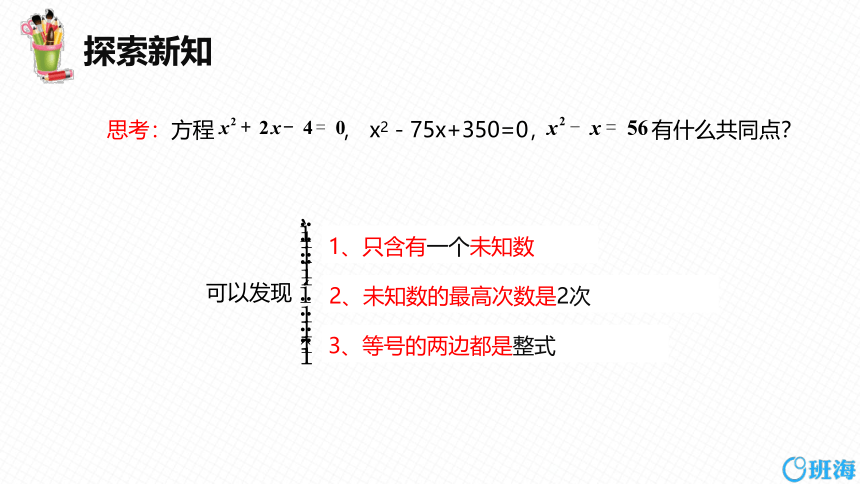
思考:方程 , x2-75x+350=0, 有什么共同点?
1、只含有一个未知数
2、未知数的最高次数是2次
3、等号的两边都是整式
可以发现
探索新知
等号两边都是整式,只含有一个未知数(一元),并且未知数的最高次数是2(二次) 的方程,叫做一元二次方程.
定义:
探索新知
例1 下列方程:①x2+y-6=0;②x2+ =2;③x2-x-2=0;
④x2-2+5x3-6x=0;⑤2x2-3x=2(x2-2),
是一元二次方程的有( )
A.1个 B. 2个 C.3个 D.4个
A
导引:
①x2+y-6=0
×
②x2+ =2
×
×
④x2-2+5x3-6x=0
有两个未知数
不是整式方程
未知数的最高次数是3
整理后二次项系数为零
×
⑤2x2-3x=2(x2-2)
只有③符合一元二次方程的定义
探索新知
总 结
一元二次方程的识别方法:
整理前:①整式方程,②只含一个未知数;
整理后:未知数的最高次数是2.
典题精讲
1.下列关于x的方程一定是一元二次方程的是( )
A.ax2+bx+c=0 B.x2+1-x2=0
C.x2+ =2 D.x2-x-2=0
2.若方程(m-1)x|m|+1-2x=3是关于x一元二次方程,则( )
A.m=1 B.m=-1
C. m=±1 D. m≠±1
D
B
探索新知
2
知识点
一元二次方程的一般形式
一般地,任何一个关于x的一元二次方程,经过整理,都能化成如下形式:ax +bx+c=0 (a≠0)这种形式叫做一元二次方程的一般形式 .
为什么规定a≠0,b,c可以为0吗?
探索新知
一元二次方程的项和各项系数
a x +b x+ c =0
二次项系数
一次项系数
a≠0
二次项
一次项
常数项
指出方程各项的系数时要带上前面的符号.
探索新知
例2 将方程3x(x-1)=5(x+2)化成一元二次方程的一般形式,并写出
其中的二次项系数、一次项系数和常数项.
解:
二次项系数
一次项系数
常数项
去括号,得3x2-3x=5x+10.
移项,合并同类项,得一元二次方程的一般形式
3x2-8x-10=0.
所以二次项系数为3,一次项系数为-8,常数项为-10.
探索新知
总 结
(1)ax2+bx+c=0,当a≠0时,方程才是一元二次方程,但b,
c可以是0.
(2)将一个一元二次方程化成一般形式,可以通过去分母、去括
号、移项、合并同类项等步骤.
(3)指出一元二次方程的某项时,应连同未知数一起;指出某项
系数时应连同它前面的符号一起.
典题精讲
1.把方程x(x+2)=5(x-2)化成一般形式,则a,b,c的值分别是( )
A.1,-3,10 B.1,7,-10
C.1,-5,12 D.1,3,2
A
2.将下列方程化成一元二次方程的一般形式,并出其中的二次项系数、
一次项系数和常数项:
(1)5x2-1=4x; (2)4x2=81;
解:移项,得5x2-4x-1=0,其中二次项系数为5,一次项系数为-4,常数项为-1.
解:移项,得4x2-81=0,其中二次项系数为4,一次项系数为0,常数项为-81.
典题精讲
2.将下列方程化成一元二次方程的一般形式,并写 出其中的二次项系
数、一次项系数和常数项:
(3)4x(x+2)=25 (4)(3x-2)(x+1)=8x-3
解:去括号,得4x2+8x=25,移项,得4x2+8x-25=0,其中二次项系数为4,一次项系数为8,常数项为-25.
解:去括号,得3x2+x-2=8x-3,移项,合并同类项,得3x2-7x+1=0,其中二次项系数为3,一次项系数为-7,常数项为1.
探索新知
3
知识点
一元二次方程的解(根)
使方程左右两边相等的未知数的值就是这个一元二次方程的解,一元二次方程的解也叫做一元二次方程的根.
探索新知
例3 下面哪些数是方程x2-x-2=0的根?
-3,-2,-1,0,1,2,3
当x=-3时,左边=9-(-3)-2=10,
则左边≠右边,
所以-3不是方程x2-x-2=0的解;
下面几个数同理可证.
经检验得-1,2为原方程的根.
解析:
探索新知
总 结
判断一个数值是不是一元二次方程的根的方法:
将这个值代入一元二次方程,看方程的左右两边是否相等,若相等,则是方程的根;若不相等,就不是方程的根.
典题精讲
方程x2+x-12=0的两个根为( )
A.x1=-2,x2=6
B.x1=-6,x2=2
C.x1=-3,x2=4
D.x1=-4,x2=3
D
探索新知
4
知识点
建立一元二次方程的模型
一元二次方程是刻画现实世界的一个有效数学模型,它是把实际问题中语言叙述的数量关系通过设未知数用一元二次方程来表达.
圆形的面积
增长(利润)率
行程问题
工程问题等
一元二次方程的模型:
常用于一元二次方程来建模的问题有:
探索新知
建立一元二次方程模型的一般步骤:
(1)审题,认真阅读题目,弄清未知量和已知量之间的关系;
(2)设出合适的未知数,一般设为x;
(3)确定等量关系;
(4)根据等量关系列出一元二次方程,有时要化为一般形式.
探索新知
例4 小雨在一幅长90 cm,宽40 cm的油画四周外围镶上一条宽度相
同的边框,制成一幅挂图并使油画画面的面积是整个挂图面积的54%,
设边框的宽度为x cm,根据题意,列出方程.
本题涉及两个基本量:油画的面积与整个挂图的面积.
在油画四周外围镶上宽度为x cm的边框,则整个挂图的长与宽各增加了多少?
利用长方形的面积公式和油画面积与整个挂图面积之间的关系列方程
x
90
40
40+2x
90+2x
解:(90+2x)(40+2x)×54%=90×40.
探索新知
总 结
建立一元二次方程模型解决实际问题时,既要根据题目条件中给出的等量关系,又要抓住题目中隐含的一些常用关系式(如面积公式、体积公式、利润公式等)进行列方程.
典题精讲
1.随州市尚市“桃花节”观赏人数逐年增加,据有关部门统计,2014
年约为20万人次,2016年约为28.8万人次,设观赏人数年均增长率
为x,则下列方程中正确的是( )
A.20(1+2x)=28.8
B.28.8(1+x)2=20
C.20(1+x2)=28.8
D. 20+(1+2x)+20(1+x)2=28.8
C
典题精讲
2.根据下列问题,列出关于x的方程,并将所列化成一元二次方程的
一般形式:
(1)4个完全相同的正方形的面积之和是25,求正 方形的边长x;
(2)一个矩形的长比宽多2,面积是100,求矩形的长x;
(3)把长为1的木条分成两段,使较短一段的长与全长的积,等于较长一段的长的平方,求较短一段的长x.
典题精讲
解:(1)列方程4x2=25,移项,得4x2-25=0.
(2)列方程x(x-2)=100,去括号,得x2-2x=100,移项,得x2-2x-100=0.
(3)列方程x 1=(1-x)2,去括号,得x=x2-2x+1,移项,合并同类项,得x2-3x+1=0.
学以致用
小试牛刀
1.等号两边都是整式,只含有______个未知数,并且未知数的最高次数
是____的方程,叫做一元二次方程.它具备三个特征:
(1)等式两边都是整式;
(2)只含______个未知数;
(3)未知数的最高次数是______.
一
2
一
2
2.一元二次方程x2-2x=1的一般形式是________________,二次项系
数是______,一次项系数是______,常数项是______.
x2-2x-1=0
1
-2
-1
小试牛刀
3.在某次聚会中,参加聚会的每两人都握了一次手,一共握了66次手,
共有多少人参加了这次聚会?
解:设有x人参加了这次聚会,则每人握了______次手,由于每两人只
握一次手,故总共握了________次手,列方程得___________,化成
一般形式为________________.
(x-1)
x2-x-132=0
小试牛刀
4.若方程 是关于x的一元二次方程,则a
的值为( )
A.±2 B.2
C.-2 D.以上都不对
B
5.一元二次方程4x2+x=1的二次项系数、一次项系数、常数项分别
是( )
A.4,0,1 B.4,1,1
C.4,1,-1 D.4,1,0
C
小试牛刀
6.若关于x的一元二次方程ax2+bx+c=0(a≠0)有一个根为-1,则下
列结论正确的是( )
A.a+b+c=1
B.a-b+c=0
C.a+b+c=0
D.a-b+c=1
B
小试牛刀
7.已知关于x的方程(m2-1)x2-(m+1)x+m=0.
(1)m为何值时,此方程为一元一次方程?
若方程为一元一次方程,则有
∴m=1.
(2)m为何值时,此方程为一元二次方程?并写出一元二次方程的二次
项系数、一次项系数及常数项.
若方程为一元二次方程,则有m2-1≠0,即m≠±1.
二次项系数:m2-1;
一次项系数:-(m+1);常数项:m.
小试牛刀
8.关于x的一元二次方程ax2+bx+c=0(a≠0)的一个根为-1,且a,
b满足等式 ,求此一元二次方程.
解:∵-1是关于x的一元二次方程ax2+bx+c=0(a≠0)的一个根,
∴a-b+c=0.
又 ,由a-2≥0,2-a≥0得a=2,∴b=-1,∴c=-3.
故这个一元二次方程为2x2-x-3=0.
小试牛刀
9.设a,b,c分别是关于x的一元二次方程的二次项系数、一次项系
数、常数项,根据下列条件,写出该一元二次方程:
(1)a∶b∶c=3∶4∶5,且a+b+c=36;
解:设一份为k,则a=3k,b=4k,c=5k,
∴3k+4k+5k=12k=36,
解得k=3.∴a=9,b=12,c=15,则方程为9x2+12x+15=0.
小试牛刀
9.设a,b,c分别是关于x的一元二次方程的二次项系数、一次项系
数、常数项,根据下列条件,写出该一元二次方程:
(2)
由非负数的性质得a-2=0,b-4=0,c-6=0,
解得a=2,b=4,c=6,则方程为2x2+4x+6=0.
课堂小结
课堂小结
一元二次方程
建立一元二次方程的模型
一元二次方程的定义
一元二次方程的根
一元二次方程的一般形式
a x +b x+ c =0
使方程两边相等的未知数的值
1.整式
2.一个未知数
3.最高次数为2
课堂小结
判别一元二次方程的“两方法”:
(1)根据定义要把握三点:一是整式方程;二是含有一个未知数;三是未知数的最高次数是2.
(2)根据一般形式要把握两点:一是能化成ax2+bx+c=0的形式,且a一定不能为0,而b,c都可以为0;二是判断是否为一元二次方程与其解的情况无关.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
21.1 一元二次方程
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
判断下列式子是否是一元一次方程:
回顾旧知
一元一次方程
1、只有一个未知数
2、未知数的指数是一次
3、方程的两边都是整式
新课精讲
探索新知
1
知识点
一元二次方程的定义
问 题(一)
如图,有一块矩形铁皮,长100 cm,宽50 cm.在它的四个角分别切去一个正方形,然后将四周突出的部分折起,就能制作一个无盖方盒.如果要制作的无盖方盒的底面积是3 600 cm2,那么铁皮各角应切去多大的正方形?
探索新知
设切去的正方形的边长是x cm,则盒底的长为(100-2x)cm,宽为
(50-2x)cm.根据方盒的底面积为3600cm2,得
(100-2x)(50-2x)=3 600.
整理,得4x2-300x+1400=0
化简,得x2-75x+350=0
解上面方程即可得出所切正方形的具体尺寸.
化简后的方程中未知数的个数和最高次数各是多少?
探索新知
问 题(二)
要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场.根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应该邀请多少个队参赛?
全部比赛场数为 4×7=28.
设应邀请x个队参赛,每个队要与其他(x-1)个队各赛一场,因为甲队对乙队的比赛和乙队对甲队的比赛是同一场比赛,所以全部比赛共 场.
列方程
整理,得
化简,得x -x=56解方程即可得出参赛队数.
探索新知
思考:方程 , x2-75x+350=0, 有什么共同点?
1、只含有一个未知数
2、未知数的最高次数是2次
3、等号的两边都是整式
可以发现
探索新知
等号两边都是整式,只含有一个未知数(一元),并且未知数的最高次数是2(二次) 的方程,叫做一元二次方程.
定义:
探索新知
例1 下列方程:①x2+y-6=0;②x2+ =2;③x2-x-2=0;
④x2-2+5x3-6x=0;⑤2x2-3x=2(x2-2),
是一元二次方程的有( )
A.1个 B. 2个 C.3个 D.4个
A
导引:
①x2+y-6=0
×
②x2+ =2
×
×
④x2-2+5x3-6x=0
有两个未知数
不是整式方程
未知数的最高次数是3
整理后二次项系数为零
×
⑤2x2-3x=2(x2-2)
只有③符合一元二次方程的定义
探索新知
总 结
一元二次方程的识别方法:
整理前:①整式方程,②只含一个未知数;
整理后:未知数的最高次数是2.
典题精讲
1.下列关于x的方程一定是一元二次方程的是( )
A.ax2+bx+c=0 B.x2+1-x2=0
C.x2+ =2 D.x2-x-2=0
2.若方程(m-1)x|m|+1-2x=3是关于x一元二次方程,则( )
A.m=1 B.m=-1
C. m=±1 D. m≠±1
D
B
探索新知
2
知识点
一元二次方程的一般形式
一般地,任何一个关于x的一元二次方程,经过整理,都能化成如下形式:ax +bx+c=0 (a≠0)这种形式叫做一元二次方程的一般形式 .
为什么规定a≠0,b,c可以为0吗?
探索新知
一元二次方程的项和各项系数
a x +b x+ c =0
二次项系数
一次项系数
a≠0
二次项
一次项
常数项
指出方程各项的系数时要带上前面的符号.
探索新知
例2 将方程3x(x-1)=5(x+2)化成一元二次方程的一般形式,并写出
其中的二次项系数、一次项系数和常数项.
解:
二次项系数
一次项系数
常数项
去括号,得3x2-3x=5x+10.
移项,合并同类项,得一元二次方程的一般形式
3x2-8x-10=0.
所以二次项系数为3,一次项系数为-8,常数项为-10.
探索新知
总 结
(1)ax2+bx+c=0,当a≠0时,方程才是一元二次方程,但b,
c可以是0.
(2)将一个一元二次方程化成一般形式,可以通过去分母、去括
号、移项、合并同类项等步骤.
(3)指出一元二次方程的某项时,应连同未知数一起;指出某项
系数时应连同它前面的符号一起.
典题精讲
1.把方程x(x+2)=5(x-2)化成一般形式,则a,b,c的值分别是( )
A.1,-3,10 B.1,7,-10
C.1,-5,12 D.1,3,2
A
2.将下列方程化成一元二次方程的一般形式,并出其中的二次项系数、
一次项系数和常数项:
(1)5x2-1=4x; (2)4x2=81;
解:移项,得5x2-4x-1=0,其中二次项系数为5,一次项系数为-4,常数项为-1.
解:移项,得4x2-81=0,其中二次项系数为4,一次项系数为0,常数项为-81.
典题精讲
2.将下列方程化成一元二次方程的一般形式,并写 出其中的二次项系
数、一次项系数和常数项:
(3)4x(x+2)=25 (4)(3x-2)(x+1)=8x-3
解:去括号,得4x2+8x=25,移项,得4x2+8x-25=0,其中二次项系数为4,一次项系数为8,常数项为-25.
解:去括号,得3x2+x-2=8x-3,移项,合并同类项,得3x2-7x+1=0,其中二次项系数为3,一次项系数为-7,常数项为1.
探索新知
3
知识点
一元二次方程的解(根)
使方程左右两边相等的未知数的值就是这个一元二次方程的解,一元二次方程的解也叫做一元二次方程的根.
探索新知
例3 下面哪些数是方程x2-x-2=0的根?
-3,-2,-1,0,1,2,3
当x=-3时,左边=9-(-3)-2=10,
则左边≠右边,
所以-3不是方程x2-x-2=0的解;
下面几个数同理可证.
经检验得-1,2为原方程的根.
解析:
探索新知
总 结
判断一个数值是不是一元二次方程的根的方法:
将这个值代入一元二次方程,看方程的左右两边是否相等,若相等,则是方程的根;若不相等,就不是方程的根.
典题精讲
方程x2+x-12=0的两个根为( )
A.x1=-2,x2=6
B.x1=-6,x2=2
C.x1=-3,x2=4
D.x1=-4,x2=3
D
探索新知
4
知识点
建立一元二次方程的模型
一元二次方程是刻画现实世界的一个有效数学模型,它是把实际问题中语言叙述的数量关系通过设未知数用一元二次方程来表达.
圆形的面积
增长(利润)率
行程问题
工程问题等
一元二次方程的模型:
常用于一元二次方程来建模的问题有:
探索新知
建立一元二次方程模型的一般步骤:
(1)审题,认真阅读题目,弄清未知量和已知量之间的关系;
(2)设出合适的未知数,一般设为x;
(3)确定等量关系;
(4)根据等量关系列出一元二次方程,有时要化为一般形式.
探索新知
例4 小雨在一幅长90 cm,宽40 cm的油画四周外围镶上一条宽度相
同的边框,制成一幅挂图并使油画画面的面积是整个挂图面积的54%,
设边框的宽度为x cm,根据题意,列出方程.
本题涉及两个基本量:油画的面积与整个挂图的面积.
在油画四周外围镶上宽度为x cm的边框,则整个挂图的长与宽各增加了多少?
利用长方形的面积公式和油画面积与整个挂图面积之间的关系列方程
x
90
40
40+2x
90+2x
解:(90+2x)(40+2x)×54%=90×40.
探索新知
总 结
建立一元二次方程模型解决实际问题时,既要根据题目条件中给出的等量关系,又要抓住题目中隐含的一些常用关系式(如面积公式、体积公式、利润公式等)进行列方程.
典题精讲
1.随州市尚市“桃花节”观赏人数逐年增加,据有关部门统计,2014
年约为20万人次,2016年约为28.8万人次,设观赏人数年均增长率
为x,则下列方程中正确的是( )
A.20(1+2x)=28.8
B.28.8(1+x)2=20
C.20(1+x2)=28.8
D. 20+(1+2x)+20(1+x)2=28.8
C
典题精讲
2.根据下列问题,列出关于x的方程,并将所列化成一元二次方程的
一般形式:
(1)4个完全相同的正方形的面积之和是25,求正 方形的边长x;
(2)一个矩形的长比宽多2,面积是100,求矩形的长x;
(3)把长为1的木条分成两段,使较短一段的长与全长的积,等于较长一段的长的平方,求较短一段的长x.
典题精讲
解:(1)列方程4x2=25,移项,得4x2-25=0.
(2)列方程x(x-2)=100,去括号,得x2-2x=100,移项,得x2-2x-100=0.
(3)列方程x 1=(1-x)2,去括号,得x=x2-2x+1,移项,合并同类项,得x2-3x+1=0.
学以致用
小试牛刀
1.等号两边都是整式,只含有______个未知数,并且未知数的最高次数
是____的方程,叫做一元二次方程.它具备三个特征:
(1)等式两边都是整式;
(2)只含______个未知数;
(3)未知数的最高次数是______.
一
2
一
2
2.一元二次方程x2-2x=1的一般形式是________________,二次项系
数是______,一次项系数是______,常数项是______.
x2-2x-1=0
1
-2
-1
小试牛刀
3.在某次聚会中,参加聚会的每两人都握了一次手,一共握了66次手,
共有多少人参加了这次聚会?
解:设有x人参加了这次聚会,则每人握了______次手,由于每两人只
握一次手,故总共握了________次手,列方程得___________,化成
一般形式为________________.
(x-1)
x2-x-132=0
小试牛刀
4.若方程 是关于x的一元二次方程,则a
的值为( )
A.±2 B.2
C.-2 D.以上都不对
B
5.一元二次方程4x2+x=1的二次项系数、一次项系数、常数项分别
是( )
A.4,0,1 B.4,1,1
C.4,1,-1 D.4,1,0
C
小试牛刀
6.若关于x的一元二次方程ax2+bx+c=0(a≠0)有一个根为-1,则下
列结论正确的是( )
A.a+b+c=1
B.a-b+c=0
C.a+b+c=0
D.a-b+c=1
B
小试牛刀
7.已知关于x的方程(m2-1)x2-(m+1)x+m=0.
(1)m为何值时,此方程为一元一次方程?
若方程为一元一次方程,则有
∴m=1.
(2)m为何值时,此方程为一元二次方程?并写出一元二次方程的二次
项系数、一次项系数及常数项.
若方程为一元二次方程,则有m2-1≠0,即m≠±1.
二次项系数:m2-1;
一次项系数:-(m+1);常数项:m.
小试牛刀
8.关于x的一元二次方程ax2+bx+c=0(a≠0)的一个根为-1,且a,
b满足等式 ,求此一元二次方程.
解:∵-1是关于x的一元二次方程ax2+bx+c=0(a≠0)的一个根,
∴a-b+c=0.
又 ,由a-2≥0,2-a≥0得a=2,∴b=-1,∴c=-3.
故这个一元二次方程为2x2-x-3=0.
小试牛刀
9.设a,b,c分别是关于x的一元二次方程的二次项系数、一次项系
数、常数项,根据下列条件,写出该一元二次方程:
(1)a∶b∶c=3∶4∶5,且a+b+c=36;
解:设一份为k,则a=3k,b=4k,c=5k,
∴3k+4k+5k=12k=36,
解得k=3.∴a=9,b=12,c=15,则方程为9x2+12x+15=0.
小试牛刀
9.设a,b,c分别是关于x的一元二次方程的二次项系数、一次项系
数、常数项,根据下列条件,写出该一元二次方程:
(2)
由非负数的性质得a-2=0,b-4=0,c-6=0,
解得a=2,b=4,c=6,则方程为2x2+4x+6=0.
课堂小结
课堂小结
一元二次方程
建立一元二次方程的模型
一元二次方程的定义
一元二次方程的根
一元二次方程的一般形式
a x +b x+ c =0
使方程两边相等的未知数的值
1.整式
2.一个未知数
3.最高次数为2
课堂小结
判别一元二次方程的“两方法”:
(1)根据定义要把握三点:一是整式方程;二是含有一个未知数;三是未知数的最高次数是2.
(2)根据一般形式要把握两点:一是能化成ax2+bx+c=0的形式,且a一定不能为0,而b,c都可以为0;二是判断是否为一元二次方程与其解的情况无关.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
