人教版(新)九上-21.2.2 公式法【优质课件】
文档属性
| 名称 | 人教版(新)九上-21.2.2 公式法【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 14:08:09 | ||
图片预览








文档简介
(共29张PPT)
21.2.2 公式法
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
配方法解一元二次方程的一般步骤:
(1)移项;
(2)二次项系数化为1;
(3)配方;
(4)开平方.
回顾旧知
新课精讲
探索新知
1
知识点
一元二次方程的求根公式
我们知道,任意一个一元二次方程都可以转化为一般形式 ax2+bx+c=0(a≠0) 你能用配方法得出它的解吗?
探索新知
解:
1.化1:把二次项系数化为1;
2.移项:把常数项移到方程的右边;
3.配方:方程两边都加上一次项系数绝对值一半的平方;
4.变形:方程左分解因式,右边合并同类项
探索新知
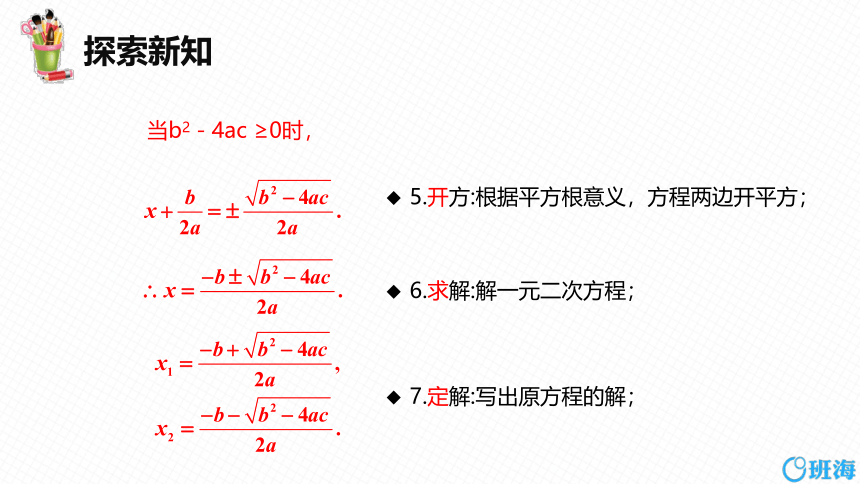
当b2-4ac ≥0时,
5.开方:根据平方根意义,方程两边开平方;
6.求解:解一元二次方程;
7.定解:写出原方程的解;
探索新知
一般地,对于一元二次方程ax2+bx+c=0(a≠0)
当b2-4ac ≥0时,它的根是:
上面这个式子称为一元二次方程的求根公式.
用求根公式解一元二次方程的方法称为公式法.
典题精讲
1.方程3x2-x=4化为一般形式后的a,b,c的值分别为( )
A.3、1、4 B.3、-1、-4
C.3、-4、-1 D.-1、3、-4
2.一元二次方程 中,b2-4ac的值应是( )
A.64 B.-64
C.32 D.-32
B
A
探索新知
2
知识点
求根公式解方程
解一个具体的一元二次方程时,把各系数直接代入求根公式,可以避免配方过程而直接得出根,这种解一元二次方程的方法叫做公式法.
确定a,b,c的值时,要注意它们的符号.
探索新知
例1 用公式法解方程:x2-4x-7=0;
a=1,b=-4,c=-7.
Δ=b2-4ac=(-4)2-4×1×(-7)=44>0.
方程有两个不等的实数根
解:
即
1.确定系数;
2.计算Δ ;
3.代入 ;
4.定根 ;
提示:方程必须要转化成一般形式才能确定系数
探索新知
例2 用公式法解下列方程:
(1) 2x2- +1=0;
解:
a=2,b= ,c=1.
Δ=b2-4ac= -4×2×1=0.
方程有两个相等的实数根
探索新知
方程化为5x2-4x-1=0.
a=5,b=-4,c=-1.
Δ=b2-4ac
=(-4)2-4×5×(-1)=36>0.
方程有两个不等的实数根
即
方程化为x2-8x+17=0.
a=1,b=-8,c=17.
Δ=b2-4ac
=(-8)2-4×1×17=-4<0.
方程无实数根.
例2 用公式法解下列方程:
(2) 5x2-3x=x+1 (3) x2+17=8x
探索新知
总 结
用公式法解一元二次方程时,应首先将方程化为一般形式,然后确定二次项系数、一次项系数及常数项,在确定了a,b,c后,先计算b2-4ac的值,当b2-4ac≥0时,再用求根公式解.
典题精讲
1.一元二次方程 的根是( )
A. B.
C. D.
C
2.已知4个数据:- ,2 ,a,b,其中a,b是方程
x2-2x-1=0的两个根,则这4个数据的中位数是( )
A.1 B.
C.2 D.
A
典题精讲
3.解下列方程:
(1) x2+x-6=0; (2)
(3) x(2x-4)=5-8x.
解:a=1,b=1,c=-6.
Δ=b2-4ac
=12-4×1×(-6)=25>0.
方程有两个不等的实数根x= ,
即x1=2,x2=-3.
a=1,b=- ,c=-.
Δ=b2-4ac
=(- )2-4×1×-14
=4>0.
方程有两个不等的实数根x= ,
即x1= ,x2 = .
典题精讲
去括号,移项,合并同类项,得
2x2+4x-5=0,a=2,b=4,c=-5.
Δ=b2-4ac=42-4×2×(-5)=56>0.
方程有两个不等的实数根x= ,
即x1= ,x2=
3.解下列方程:
(3) x(2x-4)=5-8x.
学以致用
小试牛刀
1.当Δ______时,方程ax2+bx+c=0(a≠0)的实数根可写成
_____________的形式,这个式子叫做一元二次方程ax2+
bx+c=0的求根公式.
≥0
2.利用求根公式解一元二次方程的一般步骤:先将方程化为
__________,确定a,b,c的值,同时注意它们的________;
再讨论b2-4ac的值是否为_________;最后利用__________
求方程的解.
一般形式
符号
非负数
求根公式
小试牛刀
3.方程x-5=4x2化为一般形式ax2+bx+c=0后,a,b,
c的值分别为( )
A.4,1,5 B.1,4,5
C.4,1,-5 D.4,-1,5
D
4.以x= 为根的一元二次方程可能是( )
A.x2+bx+c=0 B.x2+bx-c=0
C.x2-bx+c=0 D.x2-bx-c=0
D
小试牛刀
5.用公式法求得方程4x2-12x=3的解为( )
A.x= B.x=
C.x= D.x=
D
6.若方程(m-2)x|m|-2x+1=0是关于x的一元二次方程,则
方程的根是( )
A.x= B.x=
C.x= D.以上都不对
B
小试牛刀
7.关于x的一元二次方程(a-6)x2-8x+9=0有实数根.
(1)求a的最大整数值;
解:∵关于x的一元二次方程(a-6)x2-8x+9=0有实数根,
∴a-6≠0,Δ=(-8)2-4×(a-6)×9≥0,
解得a≤ 且a≠6.
∴a的最大整数值为7.
小试牛刀
(2)当a取最大整数值时,求出该方程的根.
当a=7时,原一元二次方程变为x2-8x+9=0,
∵a=1,b=-8,c=9,
∴Δ=(-8)2-4×1×9=28.
∴
即x1=4+ ,x2=4- .
小试牛刀
8.已知关于x的方程x2-(k+2)x+2k=0.
(1)求证:无论k取任何实数值,方程总有实数根;
证明:Δ=(k+2)2-8k=k2+4k+4-8k
=k2-4k+4=(k-2)2≥0,
故方程总有实数根.
小试牛刀
(2)若等腰△ABC的一边长a=1,另两边长b,c恰好是这个方
程的两个根,求△ABC的周长.
解:解方程x2-(k+2)x+2k=0,得x1=k,x2=2.
∵△ABC为等腰三角形,
∴当a=k=1时,另一边长为2,此时不能构成三角形;
当a=1,k=2时,△ABC的周长为5.
课堂小结
课堂小结
用公式法解一元二次方程的“四个步骤”:
(1) 把一元二次方程化为一般形式.
(2) 确定a,b,c的值.
(3) 计算b2-4ac的值.
(4) 当b2-4ac≥0时,把a,b,c的值代入求根公式,
求出方程的两个实数根;当b2-4ac<0时,方程
无实数根.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
21.2.2 公式法
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
配方法解一元二次方程的一般步骤:
(1)移项;
(2)二次项系数化为1;
(3)配方;
(4)开平方.
回顾旧知
新课精讲
探索新知
1
知识点
一元二次方程的求根公式
我们知道,任意一个一元二次方程都可以转化为一般形式 ax2+bx+c=0(a≠0) 你能用配方法得出它的解吗?
探索新知
解:
1.化1:把二次项系数化为1;
2.移项:把常数项移到方程的右边;
3.配方:方程两边都加上一次项系数绝对值一半的平方;
4.变形:方程左分解因式,右边合并同类项
探索新知
当b2-4ac ≥0时,
5.开方:根据平方根意义,方程两边开平方;
6.求解:解一元二次方程;
7.定解:写出原方程的解;
探索新知
一般地,对于一元二次方程ax2+bx+c=0(a≠0)
当b2-4ac ≥0时,它的根是:
上面这个式子称为一元二次方程的求根公式.
用求根公式解一元二次方程的方法称为公式法.
典题精讲
1.方程3x2-x=4化为一般形式后的a,b,c的值分别为( )
A.3、1、4 B.3、-1、-4
C.3、-4、-1 D.-1、3、-4
2.一元二次方程 中,b2-4ac的值应是( )
A.64 B.-64
C.32 D.-32
B
A
探索新知
2
知识点
求根公式解方程
解一个具体的一元二次方程时,把各系数直接代入求根公式,可以避免配方过程而直接得出根,这种解一元二次方程的方法叫做公式法.
确定a,b,c的值时,要注意它们的符号.
探索新知
例1 用公式法解方程:x2-4x-7=0;
a=1,b=-4,c=-7.
Δ=b2-4ac=(-4)2-4×1×(-7)=44>0.
方程有两个不等的实数根
解:
即
1.确定系数;
2.计算Δ ;
3.代入 ;
4.定根 ;
提示:方程必须要转化成一般形式才能确定系数
探索新知
例2 用公式法解下列方程:
(1) 2x2- +1=0;
解:
a=2,b= ,c=1.
Δ=b2-4ac= -4×2×1=0.
方程有两个相等的实数根
探索新知
方程化为5x2-4x-1=0.
a=5,b=-4,c=-1.
Δ=b2-4ac
=(-4)2-4×5×(-1)=36>0.
方程有两个不等的实数根
即
方程化为x2-8x+17=0.
a=1,b=-8,c=17.
Δ=b2-4ac
=(-8)2-4×1×17=-4<0.
方程无实数根.
例2 用公式法解下列方程:
(2) 5x2-3x=x+1 (3) x2+17=8x
探索新知
总 结
用公式法解一元二次方程时,应首先将方程化为一般形式,然后确定二次项系数、一次项系数及常数项,在确定了a,b,c后,先计算b2-4ac的值,当b2-4ac≥0时,再用求根公式解.
典题精讲
1.一元二次方程 的根是( )
A. B.
C. D.
C
2.已知4个数据:- ,2 ,a,b,其中a,b是方程
x2-2x-1=0的两个根,则这4个数据的中位数是( )
A.1 B.
C.2 D.
A
典题精讲
3.解下列方程:
(1) x2+x-6=0; (2)
(3) x(2x-4)=5-8x.
解:a=1,b=1,c=-6.
Δ=b2-4ac
=12-4×1×(-6)=25>0.
方程有两个不等的实数根x= ,
即x1=2,x2=-3.
a=1,b=- ,c=-.
Δ=b2-4ac
=(- )2-4×1×-14
=4>0.
方程有两个不等的实数根x= ,
即x1= ,x2 = .
典题精讲
去括号,移项,合并同类项,得
2x2+4x-5=0,a=2,b=4,c=-5.
Δ=b2-4ac=42-4×2×(-5)=56>0.
方程有两个不等的实数根x= ,
即x1= ,x2=
3.解下列方程:
(3) x(2x-4)=5-8x.
学以致用
小试牛刀
1.当Δ______时,方程ax2+bx+c=0(a≠0)的实数根可写成
_____________的形式,这个式子叫做一元二次方程ax2+
bx+c=0的求根公式.
≥0
2.利用求根公式解一元二次方程的一般步骤:先将方程化为
__________,确定a,b,c的值,同时注意它们的________;
再讨论b2-4ac的值是否为_________;最后利用__________
求方程的解.
一般形式
符号
非负数
求根公式
小试牛刀
3.方程x-5=4x2化为一般形式ax2+bx+c=0后,a,b,
c的值分别为( )
A.4,1,5 B.1,4,5
C.4,1,-5 D.4,-1,5
D
4.以x= 为根的一元二次方程可能是( )
A.x2+bx+c=0 B.x2+bx-c=0
C.x2-bx+c=0 D.x2-bx-c=0
D
小试牛刀
5.用公式法求得方程4x2-12x=3的解为( )
A.x= B.x=
C.x= D.x=
D
6.若方程(m-2)x|m|-2x+1=0是关于x的一元二次方程,则
方程的根是( )
A.x= B.x=
C.x= D.以上都不对
B
小试牛刀
7.关于x的一元二次方程(a-6)x2-8x+9=0有实数根.
(1)求a的最大整数值;
解:∵关于x的一元二次方程(a-6)x2-8x+9=0有实数根,
∴a-6≠0,Δ=(-8)2-4×(a-6)×9≥0,
解得a≤ 且a≠6.
∴a的最大整数值为7.
小试牛刀
(2)当a取最大整数值时,求出该方程的根.
当a=7时,原一元二次方程变为x2-8x+9=0,
∵a=1,b=-8,c=9,
∴Δ=(-8)2-4×1×9=28.
∴
即x1=4+ ,x2=4- .
小试牛刀
8.已知关于x的方程x2-(k+2)x+2k=0.
(1)求证:无论k取任何实数值,方程总有实数根;
证明:Δ=(k+2)2-8k=k2+4k+4-8k
=k2-4k+4=(k-2)2≥0,
故方程总有实数根.
小试牛刀
(2)若等腰△ABC的一边长a=1,另两边长b,c恰好是这个方
程的两个根,求△ABC的周长.
解:解方程x2-(k+2)x+2k=0,得x1=k,x2=2.
∵△ABC为等腰三角形,
∴当a=k=1时,另一边长为2,此时不能构成三角形;
当a=1,k=2时,△ABC的周长为5.
课堂小结
课堂小结
用公式法解一元二次方程的“四个步骤”:
(1) 把一元二次方程化为一般形式.
(2) 确定a,b,c的值.
(3) 计算b2-4ac的值.
(4) 当b2-4ac≥0时,把a,b,c的值代入求根公式,
求出方程的两个实数根;当b2-4ac<0时,方程
无实数根.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
