冀教版(新)七上-1.1 正数和负数 第二课时【优质课件】
文档属性
| 名称 | 冀教版(新)七上-1.1 正数和负数 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 15:52:49 | ||
图片预览










文档简介
(共30张PPT)
1.1 正数和负数
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图所示,小林家住黄河边的某城市,黄河
大堤高出此城区20米,另有城里铁塔高约58米,
是此城市的一大景观.小林和好朋友芳芳、徐伟 出去玩.小林站在黄河大堤上,芳芳站在地面上
放风筝,顽皮的徐伟则爬上铁塔顶.
小林说“以大堤为基准,记为0米,则芳芳所在的位置高为-20米,徐伟所在的位置高为+58米.”
徐伟说:“以铁塔顶为基准,记为0米,则芳芳所在的位置高为-58米,小林所在的位置高为-38米.”
芳芳说:“徐伟的位置比我高58米.”
他们说的数有一个统一的名称吗?
新课精讲
探索新知
1
知识点
有理数及相关概念
正数中的“+”可以省略不写,如+1.8可以写成1.8,+1 200可以写成1 200, 等等.
引入负数以后,我们学过的数可以分为:
正整数(如1,2, 3,…);
正分数(如 ,…);
0:
负整数(如-1,-2,-3,…);
负分数(如 ,… ) .
探索新知
结 论
正整数、0和负整数统称为整数,正分数和负分数统称为分数,整数和分数统称为有理数.
探索新知
在-3.5, ,0, ,0.161 616…中,有理数共有( )
A.5个 B.4个
C.3个 D.2个
例1
导引:判别有理数要紧扣其定义,也就是看这个数是不是整数或分数.
B
探索新知
总 结
(1)本例中-3.5=- ,0.161 616…= ,所以它们都是有理数:
形似分数,实质上它不是分数.分数的分子、分母应为整数(分母不为0):
(3)找各类数时,都要注意“0”的特殊性.
典题精讲
下列说法正确的有( )
①小数都是有理数:
②存在最小的自然数:
③-0.01是分数,也是有理数.
A.0个 B.1个
C.2个 D.3
1.
C
典题精讲
2. 在数0,2,-3,-1.2中,属于负整数的是( )
A.0 B.2
C.-3 D.-1.2
3. - 不属于( )
A.负数 B.分数
C.负分数 D.整数
C
D
探索新知
2
知识点
有理数的分类
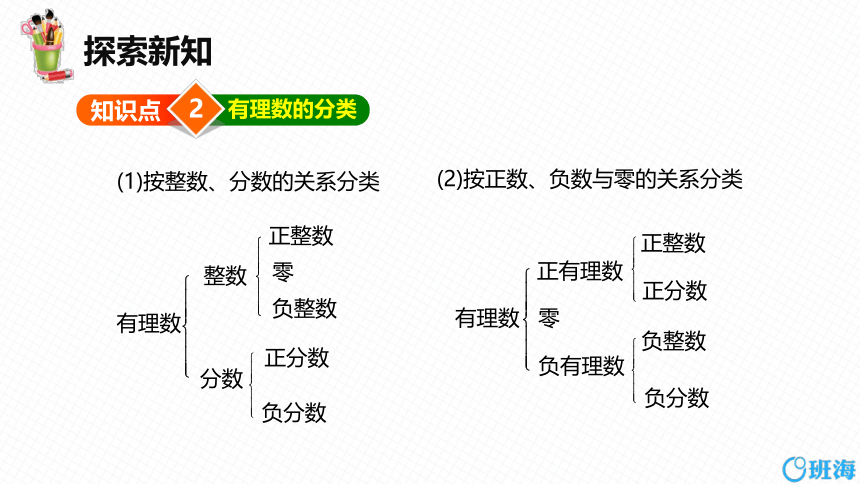
(1)按整数、分数的关系分类
有理数
整数
分数
正整数
负整数
零
负分数
正分数
有理数
正有理数
负有理数
正整数
正分数
零
负分数
负整数
(2)按正数、负数与零的关系分类
探索新知
例2 把下列各数分别填入相应的大括号里:
-2, 0, -0.314 , 25% ,11, ,-4 ,0.3,2 .
非负有理数:{ …};
整数:{ …};
自然数:{ …};
分数:{ …};
非正整数:{ …}.
导引:要严格按照各类数的概念进行填写,非负有理数包括正有理数和0:非正整数包括负整数和0.
.
0,25%,11, ,0.3,2 ,
.
-2,0,11,
0,11,
-0.314 ,25%, ,-4 ,0.3,2 ,
.
-2,0,
探索新知
总 结
(1)我们学过的数细分有五类:正整数、正分数、0、负整数、负分数,但研究问题时,通常把有理数分为三类:正有理数、0、负有理数进行讨论.
(2)通常把正数和0统称为非负数,负数和0统称为非正数,正整数和0统称为非负整数(也叫做自然数),负整数和0统称为非正整数.
(3)在对有理数进行分类时,必须按同一标准进行分类,不能混淆标准,否则会出现重复和遗漏.
1 把下列各数填在相应的大括号里.
5,-3, ,-0.373 737…,3.14,0, 9 ,- .
正数:{ …};
负数:{ …};
整数:{ …};
自然数:{ …};
负分数:{ …}.
5, ,3.14,9 ,
-3,-0.373 737… , ,
5,-3,0,
5,0,
-0.373 737… , ,
典题精讲
典题精讲
2 在有理数中,不存在( )
A.既是整数,又是负数的数
B.既不是正数,也不是负数的数
C.既是正数,又是负数的数
D.既是分数,又是负数的数
3 下列说法错误的是( )
A.负整数和负分数统称为负有理数
B.正整数、负整数和0统称为整数
C.正有理数和负有理数统称为有理数
D.0是整数,但不是分数
C
C
探索新知
3
知识点
数的集合
例3 已知A,B,C三个数集,并且每一个数集中所包含的数都写在各自的大括号内,请把这些数填在如图所示圆圈的相应位置.
A={-2,-4,-8,6.7 },
B={-4,-5,1, 2,6 } ,
C={-1,-4,-8,2,5 }.
探索新知
分析:对数集A中的每一个数应逐个分析.如-2即不属于B,也不属于C,所以应写在圆A内,但不在圆B和圆C中,-4同是属于三个数集.应写在三个数集的公共区域内:-8属于数集A和数集C,应写在圆A和C的公共区域内,但不在圆B内,其它数的写法以此类推.
解:如图所示:
本题考查数集的表示方法,注意渗透元素与集合,集合与集合的关系知识.
总 结
探索新知
1 下列选项中,所填的数正确的是( )
A.正数集合:{2,1,5, ,…}
B.非负数集合:{0,-1,-2.5,…}
C.分数集合:{-2.5,5, ,…}
D.整数集合:{ 3 ,-5,…}
2 所有的正整数和负整数合在一起构成( )
A.整数集合 B.有理数集合
C.自然数集合 D.以上说法都不对
A
D
典题精讲
典题精讲
将下列各数分别填入相应的集合里:
-1 , 2,5.7,-0.07,0,-14.01,1 .
正数集合{ …};
负分数集合{ …};
整数集合{ …}.
2,5.7,1 ,
-1 ,-0.07,-14.01,
2,0,
学以致用
小试牛刀
在数-42,+0.01,π,0,120中,正有理数是
______________.
+0.01,120
2. 观察下列数的排列规律,写出后面的三个数:
1,-2,3,-4,5,-6,____,____,____.
9
7
-8
小试牛刀
3.下列各数:+6,-8.25,-0.4, ,9, ,-28.其中负有理数有( )
A. 1个 B.2个 C.3个 D.4个
4. 在数0, , ,-8,+10,+19,+3,-3.4中,整数的个数是 ( )
A.6 B.5 C.4 D.3
D
B
小试牛刀
5.下列说法不正确的是( )
A. 0是整数 B.0是自然数
C.0是正数 D.0是有理数
6.下列说法正确的是( )
A. 有理数分为整数、分数、正有理数、零、负有理数五类
B.整数是指正整数和负整数
C.正有理数、负有理数和0构成全体有理数
D.小数就是分数
C
C
小试牛刀
7. 下列说法:
(1)-3.56既是负数、分数,也是有理数:
(2)一个分数不是正分数就是负分数:
(3)非负数包括正数和0:
(4)-2018既是负数,也是整数,但不是有理数:
(5)自然数是整数.
其中正确的个数是( )
A.1 B.2 C.3 D.4
D
课堂小结
课堂小结
1.有理数的分类:对有理数分类时,要注意分类标准,做到不重复、不遗漏;若按集合分类,则每个集合最后要加上“…”.
2.常见的三种数集的含义:
(1)非负整数集:零和正整数集(即自然数集);
(2)非负数集:零和正数集;
(3)非正数集:零和负数集.
课堂小结
3. 有理数的判别技巧:
(1) 凡是整数、分数,都是有理数.
(2) 有限小数和无限循环小数都能化为分数,所以是有理数;无限不循环小数不能化为分数,所以不是有理数.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
1.1 正数和负数
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图所示,小林家住黄河边的某城市,黄河
大堤高出此城区20米,另有城里铁塔高约58米,
是此城市的一大景观.小林和好朋友芳芳、徐伟 出去玩.小林站在黄河大堤上,芳芳站在地面上
放风筝,顽皮的徐伟则爬上铁塔顶.
小林说“以大堤为基准,记为0米,则芳芳所在的位置高为-20米,徐伟所在的位置高为+58米.”
徐伟说:“以铁塔顶为基准,记为0米,则芳芳所在的位置高为-58米,小林所在的位置高为-38米.”
芳芳说:“徐伟的位置比我高58米.”
他们说的数有一个统一的名称吗?
新课精讲
探索新知
1
知识点
有理数及相关概念
正数中的“+”可以省略不写,如+1.8可以写成1.8,+1 200可以写成1 200, 等等.
引入负数以后,我们学过的数可以分为:
正整数(如1,2, 3,…);
正分数(如 ,…);
0:
负整数(如-1,-2,-3,…);
负分数(如 ,… ) .
探索新知
结 论
正整数、0和负整数统称为整数,正分数和负分数统称为分数,整数和分数统称为有理数.
探索新知
在-3.5, ,0, ,0.161 616…中,有理数共有( )
A.5个 B.4个
C.3个 D.2个
例1
导引:判别有理数要紧扣其定义,也就是看这个数是不是整数或分数.
B
探索新知
总 结
(1)本例中-3.5=- ,0.161 616…= ,所以它们都是有理数:
形似分数,实质上它不是分数.分数的分子、分母应为整数(分母不为0):
(3)找各类数时,都要注意“0”的特殊性.
典题精讲
下列说法正确的有( )
①小数都是有理数:
②存在最小的自然数:
③-0.01是分数,也是有理数.
A.0个 B.1个
C.2个 D.3
1.
C
典题精讲
2. 在数0,2,-3,-1.2中,属于负整数的是( )
A.0 B.2
C.-3 D.-1.2
3. - 不属于( )
A.负数 B.分数
C.负分数 D.整数
C
D
探索新知
2
知识点
有理数的分类
(1)按整数、分数的关系分类
有理数
整数
分数
正整数
负整数
零
负分数
正分数
有理数
正有理数
负有理数
正整数
正分数
零
负分数
负整数
(2)按正数、负数与零的关系分类
探索新知
例2 把下列各数分别填入相应的大括号里:
-2, 0, -0.314 , 25% ,11, ,-4 ,0.3,2 .
非负有理数:{ …};
整数:{ …};
自然数:{ …};
分数:{ …};
非正整数:{ …}.
导引:要严格按照各类数的概念进行填写,非负有理数包括正有理数和0:非正整数包括负整数和0.
.
0,25%,11, ,0.3,2 ,
.
-2,0,11,
0,11,
-0.314 ,25%, ,-4 ,0.3,2 ,
.
-2,0,
探索新知
总 结
(1)我们学过的数细分有五类:正整数、正分数、0、负整数、负分数,但研究问题时,通常把有理数分为三类:正有理数、0、负有理数进行讨论.
(2)通常把正数和0统称为非负数,负数和0统称为非正数,正整数和0统称为非负整数(也叫做自然数),负整数和0统称为非正整数.
(3)在对有理数进行分类时,必须按同一标准进行分类,不能混淆标准,否则会出现重复和遗漏.
1 把下列各数填在相应的大括号里.
5,-3, ,-0.373 737…,3.14,0, 9 ,- .
正数:{ …};
负数:{ …};
整数:{ …};
自然数:{ …};
负分数:{ …}.
5, ,3.14,9 ,
-3,-0.373 737… , ,
5,-3,0,
5,0,
-0.373 737… , ,
典题精讲
典题精讲
2 在有理数中,不存在( )
A.既是整数,又是负数的数
B.既不是正数,也不是负数的数
C.既是正数,又是负数的数
D.既是分数,又是负数的数
3 下列说法错误的是( )
A.负整数和负分数统称为负有理数
B.正整数、负整数和0统称为整数
C.正有理数和负有理数统称为有理数
D.0是整数,但不是分数
C
C
探索新知
3
知识点
数的集合
例3 已知A,B,C三个数集,并且每一个数集中所包含的数都写在各自的大括号内,请把这些数填在如图所示圆圈的相应位置.
A={-2,-4,-8,6.7 },
B={-4,-5,1, 2,6 } ,
C={-1,-4,-8,2,5 }.
探索新知
分析:对数集A中的每一个数应逐个分析.如-2即不属于B,也不属于C,所以应写在圆A内,但不在圆B和圆C中,-4同是属于三个数集.应写在三个数集的公共区域内:-8属于数集A和数集C,应写在圆A和C的公共区域内,但不在圆B内,其它数的写法以此类推.
解:如图所示:
本题考查数集的表示方法,注意渗透元素与集合,集合与集合的关系知识.
总 结
探索新知
1 下列选项中,所填的数正确的是( )
A.正数集合:{2,1,5, ,…}
B.非负数集合:{0,-1,-2.5,…}
C.分数集合:{-2.5,5, ,…}
D.整数集合:{ 3 ,-5,…}
2 所有的正整数和负整数合在一起构成( )
A.整数集合 B.有理数集合
C.自然数集合 D.以上说法都不对
A
D
典题精讲
典题精讲
将下列各数分别填入相应的集合里:
-1 , 2,5.7,-0.07,0,-14.01,1 .
正数集合{ …};
负分数集合{ …};
整数集合{ …}.
2,5.7,1 ,
-1 ,-0.07,-14.01,
2,0,
学以致用
小试牛刀
在数-42,+0.01,π,0,120中,正有理数是
______________.
+0.01,120
2. 观察下列数的排列规律,写出后面的三个数:
1,-2,3,-4,5,-6,____,____,____.
9
7
-8
小试牛刀
3.下列各数:+6,-8.25,-0.4, ,9, ,-28.其中负有理数有( )
A. 1个 B.2个 C.3个 D.4个
4. 在数0, , ,-8,+10,+19,+3,-3.4中,整数的个数是 ( )
A.6 B.5 C.4 D.3
D
B
小试牛刀
5.下列说法不正确的是( )
A. 0是整数 B.0是自然数
C.0是正数 D.0是有理数
6.下列说法正确的是( )
A. 有理数分为整数、分数、正有理数、零、负有理数五类
B.整数是指正整数和负整数
C.正有理数、负有理数和0构成全体有理数
D.小数就是分数
C
C
小试牛刀
7. 下列说法:
(1)-3.56既是负数、分数,也是有理数:
(2)一个分数不是正分数就是负分数:
(3)非负数包括正数和0:
(4)-2018既是负数,也是整数,但不是有理数:
(5)自然数是整数.
其中正确的个数是( )
A.1 B.2 C.3 D.4
D
课堂小结
课堂小结
1.有理数的分类:对有理数分类时,要注意分类标准,做到不重复、不遗漏;若按集合分类,则每个集合最后要加上“…”.
2.常见的三种数集的含义:
(1)非负整数集:零和正整数集(即自然数集);
(2)非负数集:零和正数集;
(3)非正数集:零和负数集.
课堂小结
3. 有理数的判别技巧:
(1) 凡是整数、分数,都是有理数.
(2) 有限小数和无限循环小数都能化为分数,所以是有理数;无限不循环小数不能化为分数,所以不是有理数.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
