人教版(新)九上-21.3 实际问题与一元二次方程 第一课时【优质课件】
文档属性
| 名称 | 人教版(新)九上-21.3 实际问题与一元二次方程 第一课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 14:08:09 | ||
图片预览








文档简介
(共28张PPT)
21.3 实际问题
与一元二次方程
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
同一元一次方程、二元一次方程(组)等一样,一元二次方程也可以作为反映某些实际问题中数量关系的数学模型.本节继续讨论如何利用一元二次方程解决实际问题.
新课精讲
探索新知
1
知识点
增长率问题
增长率问题经常用公式 ,a为基数, b
为增长或下降后的数,x为增长率,“n”表示 n次增长
或下降.
探索新知
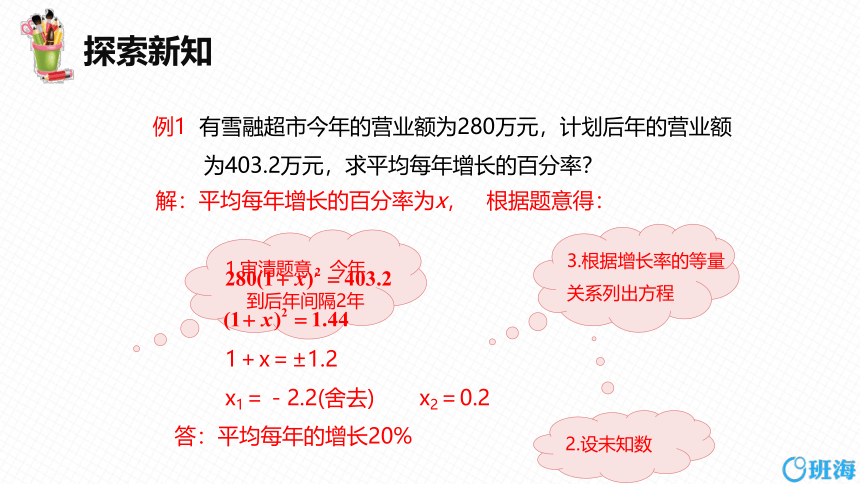
例1 有雪融超市今年的营业额为280万元,计划后年的营业额
为403.2万元,求平均每年增长的百分率?
1.审清题意,今年
到后年间隔2年
3.根据增长率的等量关系列出方程
答:平均每年的增长20%
解:平均每年增长的百分率为x, 根据题意得:
1+x=±1.2
x1=-2.2(舍去) x2=0.2
2.设未知数
探索新知
总 结
列一元二次方程解应用题的一般步骤可归结为六个字:审、设、列、解、验、答.
一般情况下, “审”不写出来,但它是关键的一步,只有审清题意,才能准确列出方程.
探索新知
例2 有一个人患了流感,经过两轮传染后共有121
个人患了流感,每轮传染中平均一个人传染了
几个人?
2
知识点
传播问题
探索新知
审清题意
设未知数
列方程
解方程验根
作 答
找出已知量、未知量
解:设平均一个人传染了x个人.则第一轮后共有(1+x)个人患了流感,第二轮后共有[1+x+x(1+x) ]个人患了流感.
依据题意得:1+x+x(1+x)=121.
解得:x1=10,x2=-12(不合题意,舍去).
平均一个人传染了10个人
典题精讲
1.早期,甲肝流行,传染性很强,曾有2人同时患上甲肝.在
一天内,一人平均能传染x人,经过两天传染后128人患上
甲肝,则x的值为( )
A.10
B.9
C.8
D.7
D
典题精讲
2.某生物实验室需培育一群有益菌.现有60个活体样本,经过
两轮培植后,总和达24 000个,其中每个有益菌每一次可分
裂出若干个相同数目的有益菌.
(1)每轮分裂中每个有益菌可分裂出多少个有益菌?
(2)按照这样的分裂速度,经过三轮培植后共有多少个有益菌?
典题精讲
解:(1)设每轮分裂中每个有益菌可分裂出x个有益菌,根据题意,得
60(1+x)2=24 000.
解得x1=19,x2=-21(不合题意,舍去).
答:每轮分裂中每个有益菌可分裂出19个有益菌.
(2)60×(1+19)3=60×203=480 000(个).
答:经过三轮培植后共有480 000个有益菌.
探索新知
3
知识点
计数问题
例3 要组织一次篮球联赛,赛制为单循环形式(每两队之
间都赛一场),计划安排15场比赛,应邀请多少个球
队参加比赛?
设应邀请x个球队参加比赛,可得到
方程可化为x2-x-30=0
解得 x1=6, x2=-5 (舍去)
所以应邀请6个球队参加比赛.
解:
探索新知
4
知识点
数字问题
例4 有一个两位数等于其各位数字之积 的3倍,其十位数字比
个位数字小2,求这个两位数.
解:
设这个两位数个位数字为x,则十位数字为
(x-2),这个两位数字是[10 (x-2) + x].
根据题意,得10 (x-2) +x=3x (x-2)整理,
得3x2-17x+20=0
解得, x1=4, x2= (不合题意,舍去)
当x=4时,x-2=2,∴这个两位数是24.
探索新知
总 结
(1)列一元二次方程解应用题时,求得的根还必须进行验根,一看是否是所列方程的根,二看是否符合问题的实际意义.如本题中解得x2= ,虽是一元二次方程的解,但由于个位数字只能取整数,故x2= 这一个根不符合实际意义,应舍去.
(2)本题采用了间接设元方式,可以使复杂的问题简单化.
典题精讲
1.一个两位数,它的十位数字比个位数字小4,若把这两个数字位
置调换,所得的两位数与原两位数的乘积等于765,求原两位数.
2.两个相邻偶数的积是168.求这两个偶数.
12和14
15
学以致用
小试牛刀
1.(1)如果增长率问题中的基数为a,平均增长率为x,则第一
次增长后的数量为____________,第二次增长后的数量为
____________.
(2)如果下降率问题中的基数为a,平均下降率为x,则第一
次下降后的数量为__________,第二次下降后的数量为
___________.
a(1+x)
a(1+x)2
a(1-x)
a(1-x)2
2.一个两位数的个位数字为a,十位数字为b,则这个两位数为
________,若交换两个数位上的数字,得到的新两位数为________.
10b+a
10a+b
小试牛刀
3.倍数传播通常涉及两个方面,一是病毒传播,二是细胞分裂.
(1)在病毒传播问题中,传染源在一轮传染后并未消失.
若开始时传染源为1,传染速度为x,则一轮后被感染的有
________;第二轮传染时,传染源为______,传染速度还是
x,则二轮后被感染的有________.
1+x
1+x
(1+x)2
(2)在细胞分裂问题中,分裂源在一轮分裂后消失了.若开始时
分裂源是1,分裂的速度是x,则一轮分裂后是______;第二
轮分裂时,分裂源为______,分裂速度还是x,则二轮分裂后
是______.
x
x
x2
小试牛刀
4.某航空公司有若干个飞机场,每两个飞机场之间都开辟一条
航线,一共开辟了15条航线,则这个航空公司共有飞机场( )
A.5个 B.6个
C.7个 D.8个
B
小试牛刀
6.为响应国家全民阅读的号召,某社区鼓励居民到社区阅览室借阅读书,
并统计每年的借阅人数和图书借阅总量(单位:本),该阅览室在2014
年图书借阅总量是7 500本,2016年图书借阅总量是10 800本.
(1)求该社区的图书借阅总量从2014年至2016年的年平均增长率;
解:设该社区的图书借阅总量从2014年至2016年的年平均增长率为x,
根据题意得7 500(1+x)2=10 800,
即(1+x)2=1.44,解得x1=0.2=20%,x2=-2.2(舍去).
答:该社区的图书借阅总量从2014年至2016年的年平均增长率为20%.
小试牛刀
(2)已知2016年该社区居民借阅图书人数有1 350人,预计2017年达到1 440人,如果2016年至2017年图书借阅总量的增长率不低于2014年至2016年的年平均增长率,那么2017年的人均借阅量比2016年增长a%,求a的值至少是多少.
10 800×(1+0.2)=12 960(本)
10 800÷1 350=8(本) 12 960÷1 440=9(本)
(9-8)÷8×100%=12.5% 故a的值至少是12.5.
小试牛刀
5.某市体育局要组织一次篮球赛,赛制为单循环形式(每两队之间
都赛一场),计划安排28场比赛,应邀请多少支球队参加比赛?
解:设应邀请x支球队参加比赛,则每队共打(x-1)场比赛,比赛总场数用代数式表示为 x(x-1).
根据题意可列出方程 x(x-1)=28.
整理,得 x2-12x=28.
解这个方程,得x1=8,x2=-7.
合乎实际意义的解为x=8. 答:应邀请8支球队参加比赛.
小试牛刀
6.一个两位数,十位上的数字与个位上的数字之和为5,把这个
两位数的十位上的数字与个位上的数字对调后,所得的新的
两位数与原来的两位数的积是736,求原来的两位数.
解:设原两位数的个位上的数字是x,则十位上的数字是(5-x),
由题意得[10(5-x)+x]·[10x+(5-x)]=736,
解得x1=2,x2=3. ∴原来的两位数是23或32.
课堂小结
课堂小结
1.列一元二次方程解实际应用问题有哪些步骤?
2.列方程解实际问题时要注意以下两点:
(1)求得的结果需要检验,看是否符合问题的实际意义.
(2)设未知数可直接设元,也可间接设元.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
21.3 实际问题
与一元二次方程
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
同一元一次方程、二元一次方程(组)等一样,一元二次方程也可以作为反映某些实际问题中数量关系的数学模型.本节继续讨论如何利用一元二次方程解决实际问题.
新课精讲
探索新知
1
知识点
增长率问题
增长率问题经常用公式 ,a为基数, b
为增长或下降后的数,x为增长率,“n”表示 n次增长
或下降.
探索新知
例1 有雪融超市今年的营业额为280万元,计划后年的营业额
为403.2万元,求平均每年增长的百分率?
1.审清题意,今年
到后年间隔2年
3.根据增长率的等量关系列出方程
答:平均每年的增长20%
解:平均每年增长的百分率为x, 根据题意得:
1+x=±1.2
x1=-2.2(舍去) x2=0.2
2.设未知数
探索新知
总 结
列一元二次方程解应用题的一般步骤可归结为六个字:审、设、列、解、验、答.
一般情况下, “审”不写出来,但它是关键的一步,只有审清题意,才能准确列出方程.
探索新知
例2 有一个人患了流感,经过两轮传染后共有121
个人患了流感,每轮传染中平均一个人传染了
几个人?
2
知识点
传播问题
探索新知
审清题意
设未知数
列方程
解方程验根
作 答
找出已知量、未知量
解:设平均一个人传染了x个人.则第一轮后共有(1+x)个人患了流感,第二轮后共有[1+x+x(1+x) ]个人患了流感.
依据题意得:1+x+x(1+x)=121.
解得:x1=10,x2=-12(不合题意,舍去).
平均一个人传染了10个人
典题精讲
1.早期,甲肝流行,传染性很强,曾有2人同时患上甲肝.在
一天内,一人平均能传染x人,经过两天传染后128人患上
甲肝,则x的值为( )
A.10
B.9
C.8
D.7
D
典题精讲
2.某生物实验室需培育一群有益菌.现有60个活体样本,经过
两轮培植后,总和达24 000个,其中每个有益菌每一次可分
裂出若干个相同数目的有益菌.
(1)每轮分裂中每个有益菌可分裂出多少个有益菌?
(2)按照这样的分裂速度,经过三轮培植后共有多少个有益菌?
典题精讲
解:(1)设每轮分裂中每个有益菌可分裂出x个有益菌,根据题意,得
60(1+x)2=24 000.
解得x1=19,x2=-21(不合题意,舍去).
答:每轮分裂中每个有益菌可分裂出19个有益菌.
(2)60×(1+19)3=60×203=480 000(个).
答:经过三轮培植后共有480 000个有益菌.
探索新知
3
知识点
计数问题
例3 要组织一次篮球联赛,赛制为单循环形式(每两队之
间都赛一场),计划安排15场比赛,应邀请多少个球
队参加比赛?
设应邀请x个球队参加比赛,可得到
方程可化为x2-x-30=0
解得 x1=6, x2=-5 (舍去)
所以应邀请6个球队参加比赛.
解:
探索新知
4
知识点
数字问题
例4 有一个两位数等于其各位数字之积 的3倍,其十位数字比
个位数字小2,求这个两位数.
解:
设这个两位数个位数字为x,则十位数字为
(x-2),这个两位数字是[10 (x-2) + x].
根据题意,得10 (x-2) +x=3x (x-2)整理,
得3x2-17x+20=0
解得, x1=4, x2= (不合题意,舍去)
当x=4时,x-2=2,∴这个两位数是24.
探索新知
总 结
(1)列一元二次方程解应用题时,求得的根还必须进行验根,一看是否是所列方程的根,二看是否符合问题的实际意义.如本题中解得x2= ,虽是一元二次方程的解,但由于个位数字只能取整数,故x2= 这一个根不符合实际意义,应舍去.
(2)本题采用了间接设元方式,可以使复杂的问题简单化.
典题精讲
1.一个两位数,它的十位数字比个位数字小4,若把这两个数字位
置调换,所得的两位数与原两位数的乘积等于765,求原两位数.
2.两个相邻偶数的积是168.求这两个偶数.
12和14
15
学以致用
小试牛刀
1.(1)如果增长率问题中的基数为a,平均增长率为x,则第一
次增长后的数量为____________,第二次增长后的数量为
____________.
(2)如果下降率问题中的基数为a,平均下降率为x,则第一
次下降后的数量为__________,第二次下降后的数量为
___________.
a(1+x)
a(1+x)2
a(1-x)
a(1-x)2
2.一个两位数的个位数字为a,十位数字为b,则这个两位数为
________,若交换两个数位上的数字,得到的新两位数为________.
10b+a
10a+b
小试牛刀
3.倍数传播通常涉及两个方面,一是病毒传播,二是细胞分裂.
(1)在病毒传播问题中,传染源在一轮传染后并未消失.
若开始时传染源为1,传染速度为x,则一轮后被感染的有
________;第二轮传染时,传染源为______,传染速度还是
x,则二轮后被感染的有________.
1+x
1+x
(1+x)2
(2)在细胞分裂问题中,分裂源在一轮分裂后消失了.若开始时
分裂源是1,分裂的速度是x,则一轮分裂后是______;第二
轮分裂时,分裂源为______,分裂速度还是x,则二轮分裂后
是______.
x
x
x2
小试牛刀
4.某航空公司有若干个飞机场,每两个飞机场之间都开辟一条
航线,一共开辟了15条航线,则这个航空公司共有飞机场( )
A.5个 B.6个
C.7个 D.8个
B
小试牛刀
6.为响应国家全民阅读的号召,某社区鼓励居民到社区阅览室借阅读书,
并统计每年的借阅人数和图书借阅总量(单位:本),该阅览室在2014
年图书借阅总量是7 500本,2016年图书借阅总量是10 800本.
(1)求该社区的图书借阅总量从2014年至2016年的年平均增长率;
解:设该社区的图书借阅总量从2014年至2016年的年平均增长率为x,
根据题意得7 500(1+x)2=10 800,
即(1+x)2=1.44,解得x1=0.2=20%,x2=-2.2(舍去).
答:该社区的图书借阅总量从2014年至2016年的年平均增长率为20%.
小试牛刀
(2)已知2016年该社区居民借阅图书人数有1 350人,预计2017年达到1 440人,如果2016年至2017年图书借阅总量的增长率不低于2014年至2016年的年平均增长率,那么2017年的人均借阅量比2016年增长a%,求a的值至少是多少.
10 800×(1+0.2)=12 960(本)
10 800÷1 350=8(本) 12 960÷1 440=9(本)
(9-8)÷8×100%=12.5% 故a的值至少是12.5.
小试牛刀
5.某市体育局要组织一次篮球赛,赛制为单循环形式(每两队之间
都赛一场),计划安排28场比赛,应邀请多少支球队参加比赛?
解:设应邀请x支球队参加比赛,则每队共打(x-1)场比赛,比赛总场数用代数式表示为 x(x-1).
根据题意可列出方程 x(x-1)=28.
整理,得 x2-12x=28.
解这个方程,得x1=8,x2=-7.
合乎实际意义的解为x=8. 答:应邀请8支球队参加比赛.
小试牛刀
6.一个两位数,十位上的数字与个位上的数字之和为5,把这个
两位数的十位上的数字与个位上的数字对调后,所得的新的
两位数与原来的两位数的积是736,求原来的两位数.
解:设原两位数的个位上的数字是x,则十位上的数字是(5-x),
由题意得[10(5-x)+x]·[10x+(5-x)]=736,
解得x1=2,x2=3. ∴原来的两位数是23或32.
课堂小结
课堂小结
1.列一元二次方程解实际应用问题有哪些步骤?
2.列方程解实际问题时要注意以下两点:
(1)求得的结果需要检验,看是否符合问题的实际意义.
(2)设未知数可直接设元,也可间接设元.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
