人教版(新)九上-22.1.1 二次函数【优质课件】
文档属性
| 名称 | 人教版(新)九上-22.1.1 二次函数【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 14:08:09 | ||
图片预览








文档简介
(共32张PPT)
22.1.1 二次函数
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
导入新知
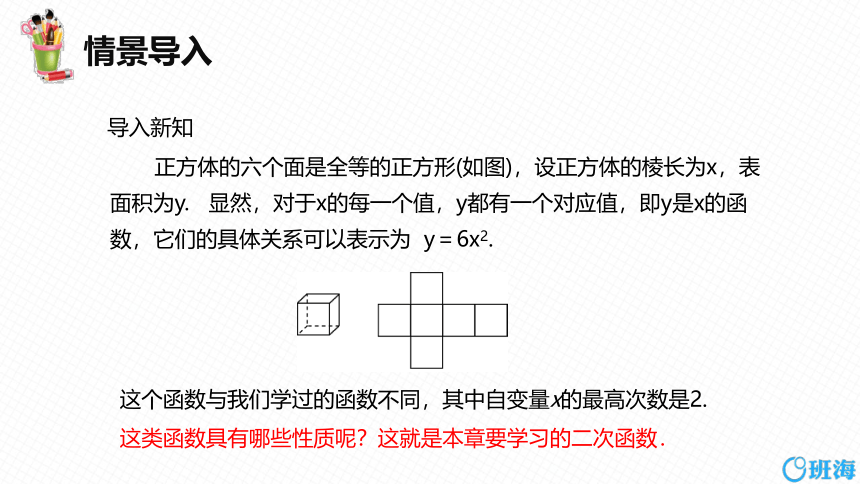
正方体的六个面是全等的正方形(如图),设正方体的棱长为x,表面积为y. 显然,对于x的每一个值,y都有一个对应值,即y是x的函数,它们的具体关系可以表示为 y=6x2.
这个函数与我们学过的函数不同,其中自变量x的最高次数是2.
这类函数具有哪些性质呢?这就是本章要学习的二次函数.
新课精讲
探索新知
1
知识点
二次函数的定义
问题1
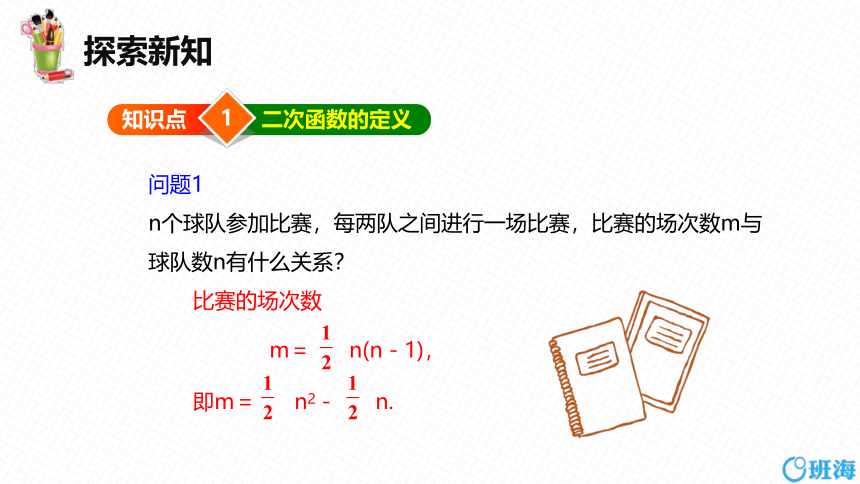
n个球队参加比赛,每两队之间进行一场比赛,比赛的场次数m与球队数n有什么关系?
比赛的场次数
m= n(n-1),
即m= n2- n.
探索新知
问题2
某种产品现在的年产量是20 t,计划今后两年增加产量.如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系应怎样表示?
两年后的产量
y=20(1+x)2,即y=20x2+40x+20.
探索新知
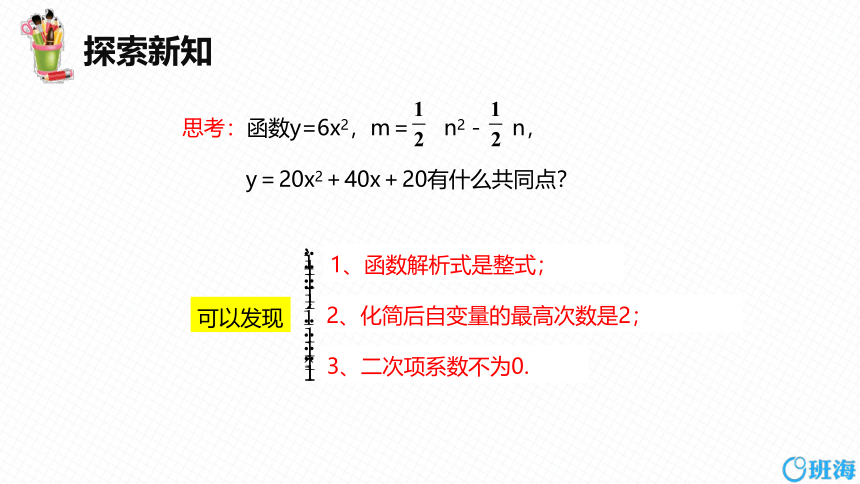
思考:函数y=6x2,m= n2- n,
y=20x2+40x+20有什么共同点?
1、函数解析式是整式;
2、化简后自变量的最高次数是2;
3、二次项系数不为0.
可以发现
探索新知
一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数,叫做二次函数.其中,x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项.
定义:
探索新知
下列函数中,哪些是二次函数?并指出二次函数的二次项系数、一次项系数和常数项.
(1)y=7x-1; (2)y=-5x2;
(3)y=3a3+2a2; (4)y=x-2+x;
(5)y=3(x-2)(x-5); (6)y=x2+ .
例1
探索新知
解:
(1)y=7x-1;
×
(2)y=-5x2;
√
(3)y=3a3+2a2;
×
自变量的最高次数是1
自变量的最高次数是2
自变量的最高次数是3
(4)y=x-2+x;
x-2不是整式
×
(5)y=3(x-2)(x-5);
整理得到y=3x2-21x+30,是二次函数
√
(6)y=x2+
不是整式
×
探索新知
解:
二次项系数
二次项系数
一次项系数
常数项
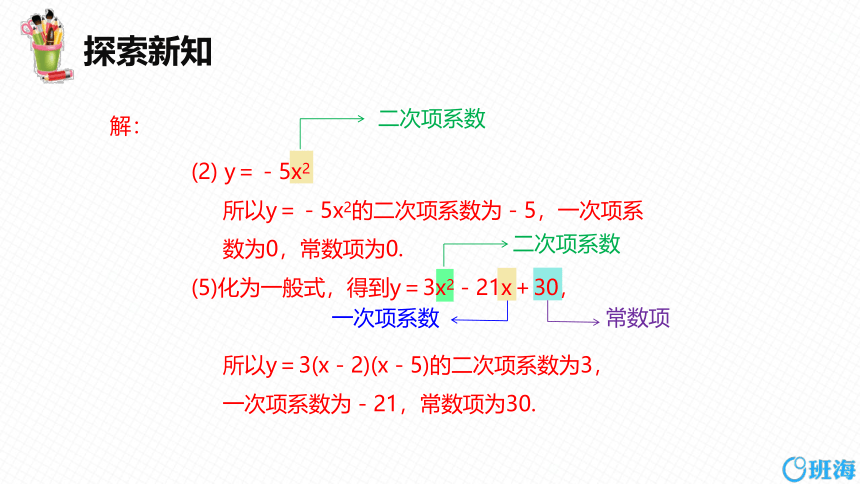
(2) y=-5x2
所以y=-5x2的二次项系数为-5,一次项系
数为0,常数项为0.
(5)化为一般式,得到y=3x2-21x+30,
所以y=3(x-2)(x-5)的二次项系数为3,
一次项系数为-21,常数项为30.
典题精讲
1.下列函数关系式中,一定为二次函数的是( )
A.y=3x-1 B.y=ax2+bx+c
C.s=2t2-2t+1 D.y=x2+
2.下列各式中,y是x的二次函数的是( )
A.y=ax2+bx+c B.x2+y-2=0
C.y2-ax=2 D.x2-y2+1=0
C
B
典题精讲
3.关于函数y=(500-10x)(40+x),下列说法不正确的是( )
A.y是x的二次函数
B.二次项系数是-10
C.一次项是100
D.常数项是20 000
C
探索新知
例2 已知函数y=(a-b)x3+2x2+2+
是y关于x的二次函数,求a,b的值.
导引:若是二次函数,则等号的右边应是关于x的二次多项式,
故a-b=0,2a+b-3=0,于是a,b可求.
解:由题意得 解得
2
知识点
二次函数的一般形式
总 结
当二次项系数是待定字母时,求出字母的值必须满足二次项系数不为0这一条件.
探索新知
探索新知
3
知识点
建立二次函数的模型
建立二次函数的模型,一般要经历以下几个步骤:
(1)确定自变量与函数代表的实际意义;
(2)找到自变量与因变量之间的等量关系,根据等量关系列出方程
或等式.
(3)将方程或等式整理成二次函数的一般形式.
探索新知
例3 填空:
(1)已知圆柱的高为14 cm,则圆柱的体积V(cm3)与底面半径r(cm)之
间的函数解析式是____________________;
(2)已知正方形的边长为10,若边长减少x,则面积减少y,y与x之间
的函数解析式是_____________________________.
导引:(1)根据圆柱体积公式V=πr 2×h求解;
(2)有三种思路:如图,①减少的面积y=S四边形AEMG+S四边形GMFD+S四边形MHCF=x(10-x)+x2+x(10-x)=-x2+20x,
②减少的面积y=S四边形AEFD+S四边形GHCD-S四边形GMFD=10x+10x-x2=-x2+20x,③减少的面积y=S四边形ABCD-S四边形EBHM=102-(10-x)2=-x2+20x.
V=14πr2(r>0)
y=-x2+20x(0≤x≤10)
探索新知
求几何问题中二次函数的解析式,除了根据有关面积、体
积公式写出二次函数解析式以外,还应考虑问题的实际
意义,明确自变量的取值(在一些问题中, 自变量的取值
可能是整数或者是在一定的范围内);
(2) 判断自变量的取值范围,应结合问题,考虑全面,不要漏
掉一些约束条件.列不等式组是求自变量的取值范围的常
见方法.
总 结
典题精讲
一台机器原价60万元,如果每年的折旧率为x,两年后这台机器的
价格为y万元,则y与x之间的函数关系式为( )
A.y=60(1-x)2
B.y=60(1-x)
C.y=60-x2
D.y=60(1+x)2
A
学以致用
小试牛刀
1.一般地,若两个变量x,y之间的对应关系可以表示成y=____________
(a,b,c是常数,a≠0)的形式,则称y是x的二次函数;一个函数是二
次函数,经过整理后必须同时满足以下三个条件:
(1)关于自变量的式子是________;
(2)自变量的最高次数是________;
(3)二次项系数________.
ax2+bx+c
整式
2
不为0
小试牛刀
3.建立二次函数的模型一般经过________题意,找___________,列
__________解析式这三个步骤.
审清
等量关系
二次函数
2.任何一个二次函数的解析式都可化为y=ax2+bx+c(a≠0)的形式,
其中x是______________,a,b,c分别是函数解析式的二次项系数、
____________________和常数项.
自变量
一次项系数
小试牛刀
4.下列函数关系式中,一定为二次函数的是( )
A.y=3x-1 B.y=ax2+bx+c
C.s=2t2-2t+1 D.y=x2+
C
5.下列各式中,y是x的二次函数的是( )
A.y= B.y=x2+ +1
C.y=2x2-1 D.y=
C
小试牛刀
6.已知二次函数y=2-3x+x2,则其二次项系数a、一次项系数b、
常数项c分别为( )
A.a=2,b=-3,c=1 B.a=2,b=3,c=1
C.a=1,b=3,c=2 D.a=1,b=-3,c=2
D
7.二次函数y=x2+bx+c中,若b+c=0,则它的图象一定经过点( )
A.(1,-1) B.(-1,1)
C.(-1,-1) D.(1,1)
D
小试牛刀
8.某商场每件进价为80元的某种商品原来按每件100元出售,一天可
售出100件.为了扩大销售,增加盈利,尽量减少库存,商场决定
采取适当的降价措施,经调查发现,这种商品每降价1元,其销量
可增加10件.
(1)求商场经营该商品原来一天可获利多少元.
解:商场经营该商品原来一天可获利:
100×(100-80)=2 000(元).
小试牛刀
(2)设后来该商品每件降价x元,商场一天可获利y元.
①若商场经营该商品一天要获利2 160元,则每件商品要降价多少元?
②求y与x之间的函数关系式.
①依题意,得(100-80-x)(100+10x)=2 160,
即x2-10x+16=0, 解得x1=2,x2=8.
为了尽量减少库存,所以x应取8,即每件商品要降价8元.
②依题意,得:
y=(100-80-x)(100+10x)=-10x2+100x+2 000.
小试牛刀
9.一个花园门的形状如图所示,它的上部分是半圆,下部分是矩形,
矩形的高是2.5 m.
(1)求花园门的面积S(m2)关于上部分半圆的半径r(m)之间的函数关系式;
解:S= πr2+2r×2.5= πr2+5r
小试牛刀
(2)求当上部分半圆的半径为2 m时,花园门的面积(结果精确到0.1 m2).
当r=2时,
S= πr2+5r
= ×π×22+5×2≈16.3.
答:花园门的面积约为16.3 m2.
课堂小结
课堂小结
二次函数的定义要理解三点:
(1)函数关系式必须是整式,自变量的取值是全体实数;而在实际应用中,自变量的取值必须符合实际意义.
(2)确定二次函数的各项系数及常数项时,要把函数关系式化为一般形式.
(3)二次项系数不为0.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
22.1.1 二次函数
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
导入新知
正方体的六个面是全等的正方形(如图),设正方体的棱长为x,表面积为y. 显然,对于x的每一个值,y都有一个对应值,即y是x的函数,它们的具体关系可以表示为 y=6x2.
这个函数与我们学过的函数不同,其中自变量x的最高次数是2.
这类函数具有哪些性质呢?这就是本章要学习的二次函数.
新课精讲
探索新知
1
知识点
二次函数的定义
问题1
n个球队参加比赛,每两队之间进行一场比赛,比赛的场次数m与球队数n有什么关系?
比赛的场次数
m= n(n-1),
即m= n2- n.
探索新知
问题2
某种产品现在的年产量是20 t,计划今后两年增加产量.如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系应怎样表示?
两年后的产量
y=20(1+x)2,即y=20x2+40x+20.
探索新知
思考:函数y=6x2,m= n2- n,
y=20x2+40x+20有什么共同点?
1、函数解析式是整式;
2、化简后自变量的最高次数是2;
3、二次项系数不为0.
可以发现
探索新知
一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数,叫做二次函数.其中,x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项.
定义:
探索新知
下列函数中,哪些是二次函数?并指出二次函数的二次项系数、一次项系数和常数项.
(1)y=7x-1; (2)y=-5x2;
(3)y=3a3+2a2; (4)y=x-2+x;
(5)y=3(x-2)(x-5); (6)y=x2+ .
例1
探索新知
解:
(1)y=7x-1;
×
(2)y=-5x2;
√
(3)y=3a3+2a2;
×
自变量的最高次数是1
自变量的最高次数是2
自变量的最高次数是3
(4)y=x-2+x;
x-2不是整式
×
(5)y=3(x-2)(x-5);
整理得到y=3x2-21x+30,是二次函数
√
(6)y=x2+
不是整式
×
探索新知
解:
二次项系数
二次项系数
一次项系数
常数项
(2) y=-5x2
所以y=-5x2的二次项系数为-5,一次项系
数为0,常数项为0.
(5)化为一般式,得到y=3x2-21x+30,
所以y=3(x-2)(x-5)的二次项系数为3,
一次项系数为-21,常数项为30.
典题精讲
1.下列函数关系式中,一定为二次函数的是( )
A.y=3x-1 B.y=ax2+bx+c
C.s=2t2-2t+1 D.y=x2+
2.下列各式中,y是x的二次函数的是( )
A.y=ax2+bx+c B.x2+y-2=0
C.y2-ax=2 D.x2-y2+1=0
C
B
典题精讲
3.关于函数y=(500-10x)(40+x),下列说法不正确的是( )
A.y是x的二次函数
B.二次项系数是-10
C.一次项是100
D.常数项是20 000
C
探索新知
例2 已知函数y=(a-b)x3+2x2+2+
是y关于x的二次函数,求a,b的值.
导引:若是二次函数,则等号的右边应是关于x的二次多项式,
故a-b=0,2a+b-3=0,于是a,b可求.
解:由题意得 解得
2
知识点
二次函数的一般形式
总 结
当二次项系数是待定字母时,求出字母的值必须满足二次项系数不为0这一条件.
探索新知
探索新知
3
知识点
建立二次函数的模型
建立二次函数的模型,一般要经历以下几个步骤:
(1)确定自变量与函数代表的实际意义;
(2)找到自变量与因变量之间的等量关系,根据等量关系列出方程
或等式.
(3)将方程或等式整理成二次函数的一般形式.
探索新知
例3 填空:
(1)已知圆柱的高为14 cm,则圆柱的体积V(cm3)与底面半径r(cm)之
间的函数解析式是____________________;
(2)已知正方形的边长为10,若边长减少x,则面积减少y,y与x之间
的函数解析式是_____________________________.
导引:(1)根据圆柱体积公式V=πr 2×h求解;
(2)有三种思路:如图,①减少的面积y=S四边形AEMG+S四边形GMFD+S四边形MHCF=x(10-x)+x2+x(10-x)=-x2+20x,
②减少的面积y=S四边形AEFD+S四边形GHCD-S四边形GMFD=10x+10x-x2=-x2+20x,③减少的面积y=S四边形ABCD-S四边形EBHM=102-(10-x)2=-x2+20x.
V=14πr2(r>0)
y=-x2+20x(0≤x≤10)
探索新知
求几何问题中二次函数的解析式,除了根据有关面积、体
积公式写出二次函数解析式以外,还应考虑问题的实际
意义,明确自变量的取值(在一些问题中, 自变量的取值
可能是整数或者是在一定的范围内);
(2) 判断自变量的取值范围,应结合问题,考虑全面,不要漏
掉一些约束条件.列不等式组是求自变量的取值范围的常
见方法.
总 结
典题精讲
一台机器原价60万元,如果每年的折旧率为x,两年后这台机器的
价格为y万元,则y与x之间的函数关系式为( )
A.y=60(1-x)2
B.y=60(1-x)
C.y=60-x2
D.y=60(1+x)2
A
学以致用
小试牛刀
1.一般地,若两个变量x,y之间的对应关系可以表示成y=____________
(a,b,c是常数,a≠0)的形式,则称y是x的二次函数;一个函数是二
次函数,经过整理后必须同时满足以下三个条件:
(1)关于自变量的式子是________;
(2)自变量的最高次数是________;
(3)二次项系数________.
ax2+bx+c
整式
2
不为0
小试牛刀
3.建立二次函数的模型一般经过________题意,找___________,列
__________解析式这三个步骤.
审清
等量关系
二次函数
2.任何一个二次函数的解析式都可化为y=ax2+bx+c(a≠0)的形式,
其中x是______________,a,b,c分别是函数解析式的二次项系数、
____________________和常数项.
自变量
一次项系数
小试牛刀
4.下列函数关系式中,一定为二次函数的是( )
A.y=3x-1 B.y=ax2+bx+c
C.s=2t2-2t+1 D.y=x2+
C
5.下列各式中,y是x的二次函数的是( )
A.y= B.y=x2+ +1
C.y=2x2-1 D.y=
C
小试牛刀
6.已知二次函数y=2-3x+x2,则其二次项系数a、一次项系数b、
常数项c分别为( )
A.a=2,b=-3,c=1 B.a=2,b=3,c=1
C.a=1,b=3,c=2 D.a=1,b=-3,c=2
D
7.二次函数y=x2+bx+c中,若b+c=0,则它的图象一定经过点( )
A.(1,-1) B.(-1,1)
C.(-1,-1) D.(1,1)
D
小试牛刀
8.某商场每件进价为80元的某种商品原来按每件100元出售,一天可
售出100件.为了扩大销售,增加盈利,尽量减少库存,商场决定
采取适当的降价措施,经调查发现,这种商品每降价1元,其销量
可增加10件.
(1)求商场经营该商品原来一天可获利多少元.
解:商场经营该商品原来一天可获利:
100×(100-80)=2 000(元).
小试牛刀
(2)设后来该商品每件降价x元,商场一天可获利y元.
①若商场经营该商品一天要获利2 160元,则每件商品要降价多少元?
②求y与x之间的函数关系式.
①依题意,得(100-80-x)(100+10x)=2 160,
即x2-10x+16=0, 解得x1=2,x2=8.
为了尽量减少库存,所以x应取8,即每件商品要降价8元.
②依题意,得:
y=(100-80-x)(100+10x)=-10x2+100x+2 000.
小试牛刀
9.一个花园门的形状如图所示,它的上部分是半圆,下部分是矩形,
矩形的高是2.5 m.
(1)求花园门的面积S(m2)关于上部分半圆的半径r(m)之间的函数关系式;
解:S= πr2+2r×2.5= πr2+5r
小试牛刀
(2)求当上部分半圆的半径为2 m时,花园门的面积(结果精确到0.1 m2).
当r=2时,
S= πr2+5r
= ×π×22+5×2≈16.3.
答:花园门的面积约为16.3 m2.
课堂小结
课堂小结
二次函数的定义要理解三点:
(1)函数关系式必须是整式,自变量的取值是全体实数;而在实际应用中,自变量的取值必须符合实际意义.
(2)确定二次函数的各项系数及常数项时,要把函数关系式化为一般形式.
(3)二次项系数不为0.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
