人教版(新)九上-22.1.3 二次函数y=a(x-h)2+k图象和性质 第三课时【优质课件】
文档属性
| 名称 | 人教版(新)九上-22.1.3 二次函数y=a(x-h)2+k图象和性质 第三课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览











文档简介
(共39张PPT)
22.1.3 二次函数y=a(x-h) +k图象和性质
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
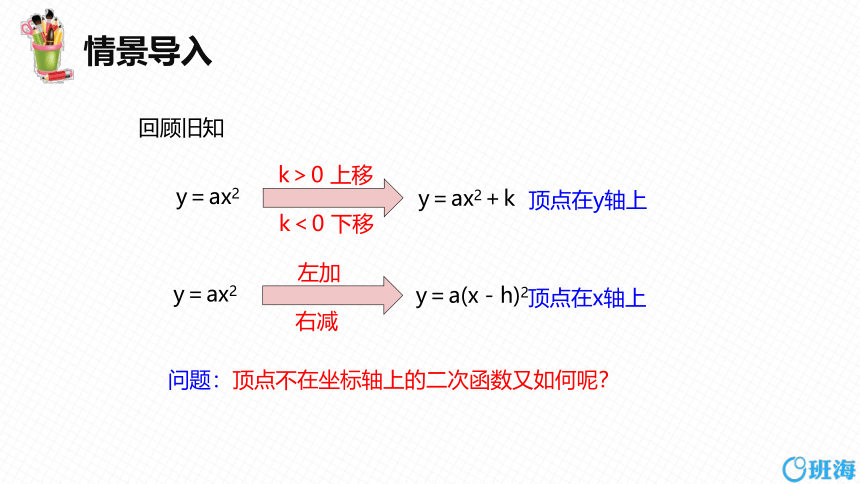
回顾旧知
y=ax2
k>0 上移
y=ax2+k
y=ax2
y=a(x-h)2
k<0 下移
顶点在y轴上
左加
右减
顶点在x轴上
问题:顶点不在坐标轴上的二次函数又如何呢?
新课精讲
探索新知
1
知识点
二次函数y=a(x-h)2+k的图象
通过观察抛物线y=- (x+1)2 -1,你能得出抛物
线y=a(x-h)2+k有怎样的几何性质?
探索新知
归 纳
抛物线y=a(x-h)2+k有如下特点:
(1)当a>0时,开口向上;当a<0时,开口向下.
(2)对称轴是x=h.
(3)顶点是(h,k).
探索新知
例1 对于抛物线y=- (x+1)2+3,下列结论:①抛物线的开口
向下;②对称轴为直线x=1;③顶点坐标为(-1, 3),其中
正确结论的个数为( )
A.0 B.1 C.2 D.3
由二次函数y=- (x+1)2+3的解析式知,a=- <0,
∴抛物线开口向下;∵h=-1,
∴抛物线的对称轴为x=-1;由h=-1,k=3
可得顶点坐标为(-1,3).
C
导引:
探索新知
利用抛物线y=a(x-h)2+k(顶点式)中的顶点坐标,对称轴等公式解题,首先必须熟记它们之间与解析式中a,h,k之间的关系,再结合题中给出的相关条件及已学的相关知识按题目的要求解题.
总 结
探索新知
例2 要修建一个圆形喷水池,在池中心竖直安装一根水管,在
水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池
中心的水平距离为1 m处达到最高,高度为3 m,水柱落
地处离池中心3 m,水管应多长?
如图,以水管与地面交点为原点,原点与水柱落地处所在直线为x轴,水管所在直线为y轴,建立直角坐标系.
解:
探索新知
点(1,3)是图中这段抛物线的顶点,因此可设这段抛物线对应的函数解析式是
y=a(x-1)2+3(0≤x≤3).
由这段抛物线经过点(3,0),可得
0=a(3-1)2+3,解得a=-
因此y=- (x-1)2+3(0≤x≤3).
当x=0时,y=2.25,也就是说,水管应2.25 m长.
典题精讲
1.抛物线y=2(x-3)2+1的顶点坐标是( )
A.(3,1) B.(3,-1)
C.(-3,1) D.(-3,-1)
A
2.抛物线y=(x-1)2-3的对称轴是( )
A.y轴 B.直线x=-1
C.直线x=1 D.直线x=-3
C
典题精讲
3.若抛物线y=(x-m)2+(m+1)的顶点在第一象限,则m的取值
范围为( )
A.m>1
B.m>0
C.m>-1
D.-1<m<0
B
探索新知
2
知识点
二次函数y=a(x-h)2+k的性质
通过观察抛物线y=- (x+1)2 -1,你能得出二次函数y=a(x-h)2+k有怎样的代数性质?
探索新知
归 纳
y=a(x-h)2+k的代数性质:
(1)当a>0时,函数有最小值k,当a<0时,函数有最大值k.
(2)如果a>0,当xh时,y随x的
增大而增大;如果a<0,当xh
时,y随x的增大而减小.
探索新知
例3 已知点A(4,y1),B( ,y2),C(-2,y3)都在二次函数
y=(x-2)2-1的图象上,比较y1,y2,y3的大小关系.
思路一:由顶点式可知抛物线的对称轴是直线x=2, A、B、C三点在对称轴两侧,可以利用A点的对称点转化到对称轴左侧,依据开口向上和在对称轴左侧y随x的增大而减小进行比较大小;
导引:
探索新知
思路二:二次函数解析式和三个点的横坐标都是已知的,可以把点的坐标代入解析式求三个点的纵坐标,然后比较大小;
思路三:抛物线开口向上,顶点纵坐标最小,由图象的变化趋势可知抛物线上的点距离对称轴越近 (即离顶点越近)纵坐标越小,从而进行比较大小.
探索新知
方法一:∵y=(x-2)2-1,∴对称轴为直线x=2.
∴点A(4,y1)关于x=2的对称点是(0,y1).
∵-2<0< 且a=1>0,∴y2方法二:∵A(4,y1),B( ,y2),C(-2, y3)
在抛物线y=(x-2)2-1上.
∴y1=3,y2=5-4 ,y3=15.
∵5-4 <3<15,∴y2解:
探索新知
方法三:设点A、B、C三点到抛物线对称轴的距离分别为d1、d2、d3.
∵y=(x-2)2-1,∴对称轴为直线x=2.
∴d1=2,d2=2- ,d3=4,
∵2- <2<4,且a=1>0,
∴y2探索新知
抛物线上点的纵坐标比较大小的基本方法:
(1)把各点利用抛物线上的对称点的纵坐标相等,把各点转化
到对称轴的同侧,再利用二次函数的增减性进行比较大小;
(2)当已知具体的抛物线的解析式及相应点的横坐标确定时,
可先求出相应点的纵坐标,然后比较大小;
(3)利用“开口向上,抛物线上的点距离对称轴越近,点的纵
坐标越小,开口向下,抛物线上的点距离对称轴越近,
点的纵坐标越大”也可以比较大小.
总 结
探索新知
3
知识点
二次函数y=a(x-h)2+k与y=ax2之间的关系
思考:抛物线y=a(x-h)2+k与抛物线y=ax2有怎样的关系?
探索新知
探索新知
归 纳
一般地,抛物线y=a(x-h)2+k与y=ax2形状相同,位置不同.把抛物线y=ax2向上(下)向左(右)平移,可以得到抛物线y=a(x-h)2+k.平移的方向、距离要根据h,k的值来决定.
探索新知
例4 将抛物线y=x2向右平移2个单位,再向上平移3个单位后,
抛物线的解析式为( )
A.y=(x+2)2+3 B. y=(x-2)2+3
C.y=(x+2)2-3 D. y=(x-2)2-3
先根据二次函数图象的平移规律,对自变量和函数值作相
应的变化,写出变化后的二次函数表达式,再选出正确的项.
由二次函数图象的平移规律可知,将抛物线y=x2先向右平移
2个单位所得抛物线的表达式为:y=(x-2)2,再向上平移3
个单位后,所得函数的表达式为y=(x-2)2+3,故应选B.
B
导引:
解:
探索新知
抛物线的平移遵循“左加右减,上加下减”的原则,具体为:
(1)上下平移:抛物线y=a(x-h)2+k向上平移m(m>0)个单位,
所得抛物线的解析式为y=a(x-h)2+k+m;抛物线y=a(x-
h)2+k向下平移m(m>0)个单位,所得抛物线的解析式
为y=a(x-h)2+k-m.
(2)左右平移:抛物线y=a(x-h)2+k向左平移n(n>0)个单位,
所得抛物线的解析式为y=a(x-h+n)2+k;抛物线y=a(x-
h)2+k向右平移n(n>0)个单位,所得抛物线的解析式为
y=a(x-h-n)2+k.特别地,要注意其中的符号处理.
典题精讲
1.设抛物线C1:y=x2向右平移2个单位长度,向下平移3个单位
长度得到抛物线C2,则抛物线C2对应的函数解析式是( )
A.y=(x-2)2-3 B.y=(x+2)2-3
C.y=(x-2)2+3 D.y=(x+2)2+3
A
2.将抛物线y=x2+1先向左平移2个单位长度,再向下平移3个
单位长度,所得抛物线对应的函数解析式是( )
A.y=(x+2)2+2 B.y=(x+2)2-2
C.y=(x-2)2+2 D.y=(x-2)2-2
B
学以致用
小试牛刀
1.二次函数y=a(x-h)2+k的图象的特征:
(1)a>0,开口________,a<0,开口________;
(2)对称轴是直线________,顶点坐标为________.
向上
向下
x=h
(h,k)
2.二次函数y=a(x-h)2+k的性质:
若a>0,当x>h时,y随x的增大而______;当xy随x的增大而______;当x=h时,y取最_____值_______.
若a<0,当x>h时,y随x的增大而________;当xy随x的增大而________;当x=h时,y取最________值k.
增大
减小
小
k
减小
增大
大
小试牛刀
3.抛物线y=a(x-h)2+k与y=ax2形状______,位置______.把抛物
线y=ax2向上(下)或左(右)平移,可以得到抛物线y=a(x-h)2+k,
平移的方向、距离要根据________的值来决定.
相同
不同
h,k
4.抛物线 的顶点坐标是( )
A. ,-3 B. - ,-3
C. ,3 D. - ,3
B
小试牛刀
5.二次函数y=(x+2)2-1的图象大致为( )
D
6.已知二次函数y=(x-h)2+1(h为常数),在自变量x的值满足1≤x
≤3的情况下,与其对应的函数值y的最小值为5,则h的值为( )
A.1或-5 B.-1或5
C.1或-3 D.1或3
B
小试牛刀
7.如图,在△ABC中,∠C=90°,AB=10 cm,BC=8 cm,点
P从点A沿AC向点C以1 cm/s的速度运动,同时点Q从点C沿
CB向点B以2 cm/s的速度运动(点Q运动到点B停止),在运动
过程中,四边形PABQ的面积的最小值为( )
A.19 cm2 B.16 cm2
C.15 cm2 D.12 cm2
C
小试牛刀
8.把二次函数y=a(x-h)2+k的图象先向左平移2个单位长度,再
向上平移4个单位长度,得到二次函数y= (x+1)2-1的图象.
(1)试确定a,h,k的值;
a= ,h=1,k=-5.
(2)指出二次函数y=a(x-h)2+k的图象的开口方向、对称轴和顶点坐标.
图象的开口向上,对称轴为直线x=1,
顶点坐标为(1,-5).
小试牛刀
9.如图,已知抛物线y=a(x-h)2+k与x轴的一个交
点为A(3,0),与y轴的交点为B(0,3),对称轴为
直线x=1.
(1)求抛物线对应的函数解析式;
由题意可知h=1,则y=a(x-1)2+k.将点(3,0),(0,3)的坐标代入上式,得:
故抛物线对应的函数解析式为y=-(x-1)2+4.
解得
小试牛刀
(2)已知点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标.
①当MA=MB时,M(0,0);
②当AB=AM时,M(0,-3);
③当AB=BM时,M(0,3+ )或M(0,3- ).
所以点M的坐标为(0,0),(0,-3),(0,3+ )
或(0,3- ).
小试牛刀
10.某广场中心有高低不同的各种喷泉,其中一支高度为1 m的
喷水管喷出的抛物线型水柱最大高度为3 m,此时距喷水管
的水平距离为 m,求在如图所示的平面直角坐标系中抛
物线型水柱对应的函数解析式(不要
求写出自变量的取值范围).
小试牛刀
解:∵点( ,3)是抛物线的顶点,
∴可设抛物线型水柱对应的函数解析式为
y=a(x- )2+3. ∵抛物线经过点(0,1),
∴1=(0- )2 a+3,解得a=-8.
∴抛物线型水柱对应的函数解析式为:
y=-8(x- )2+3.
课堂小结
课堂小结
二次函数y=a(x-h)2+k的图象与性质:
二次函数解析式 a的 符号 开口方向 对称轴 顶点坐标 增减性 最值
y= a(x-h)2+k a>0 向上 直线x=h (h,k) 当x>h时,y随x的增大而增大;当x<h时,y随x的增大而减小 当x=时,
y最小值
=k
a<0 向下 直线x=h (h,k) 当x<h时,y随x的增大而增大;当x>h时,y随x的增大而减小 当x=时,
y最大值=k
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
22.1.3 二次函数y=a(x-h) +k图象和性质
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
回顾旧知
y=ax2
k>0 上移
y=ax2+k
y=ax2
y=a(x-h)2
k<0 下移
顶点在y轴上
左加
右减
顶点在x轴上
问题:顶点不在坐标轴上的二次函数又如何呢?
新课精讲
探索新知
1
知识点
二次函数y=a(x-h)2+k的图象
通过观察抛物线y=- (x+1)2 -1,你能得出抛物
线y=a(x-h)2+k有怎样的几何性质?
探索新知
归 纳
抛物线y=a(x-h)2+k有如下特点:
(1)当a>0时,开口向上;当a<0时,开口向下.
(2)对称轴是x=h.
(3)顶点是(h,k).
探索新知
例1 对于抛物线y=- (x+1)2+3,下列结论:①抛物线的开口
向下;②对称轴为直线x=1;③顶点坐标为(-1, 3),其中
正确结论的个数为( )
A.0 B.1 C.2 D.3
由二次函数y=- (x+1)2+3的解析式知,a=- <0,
∴抛物线开口向下;∵h=-1,
∴抛物线的对称轴为x=-1;由h=-1,k=3
可得顶点坐标为(-1,3).
C
导引:
探索新知
利用抛物线y=a(x-h)2+k(顶点式)中的顶点坐标,对称轴等公式解题,首先必须熟记它们之间与解析式中a,h,k之间的关系,再结合题中给出的相关条件及已学的相关知识按题目的要求解题.
总 结
探索新知
例2 要修建一个圆形喷水池,在池中心竖直安装一根水管,在
水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池
中心的水平距离为1 m处达到最高,高度为3 m,水柱落
地处离池中心3 m,水管应多长?
如图,以水管与地面交点为原点,原点与水柱落地处所在直线为x轴,水管所在直线为y轴,建立直角坐标系.
解:
探索新知
点(1,3)是图中这段抛物线的顶点,因此可设这段抛物线对应的函数解析式是
y=a(x-1)2+3(0≤x≤3).
由这段抛物线经过点(3,0),可得
0=a(3-1)2+3,解得a=-
因此y=- (x-1)2+3(0≤x≤3).
当x=0时,y=2.25,也就是说,水管应2.25 m长.
典题精讲
1.抛物线y=2(x-3)2+1的顶点坐标是( )
A.(3,1) B.(3,-1)
C.(-3,1) D.(-3,-1)
A
2.抛物线y=(x-1)2-3的对称轴是( )
A.y轴 B.直线x=-1
C.直线x=1 D.直线x=-3
C
典题精讲
3.若抛物线y=(x-m)2+(m+1)的顶点在第一象限,则m的取值
范围为( )
A.m>1
B.m>0
C.m>-1
D.-1<m<0
B
探索新知
2
知识点
二次函数y=a(x-h)2+k的性质
通过观察抛物线y=- (x+1)2 -1,你能得出二次函数y=a(x-h)2+k有怎样的代数性质?
探索新知
归 纳
y=a(x-h)2+k的代数性质:
(1)当a>0时,函数有最小值k,当a<0时,函数有最大值k.
(2)如果a>0,当x
增大而增大;如果a<0,当x
时,y随x的增大而减小.
探索新知
例3 已知点A(4,y1),B( ,y2),C(-2,y3)都在二次函数
y=(x-2)2-1的图象上,比较y1,y2,y3的大小关系.
思路一:由顶点式可知抛物线的对称轴是直线x=2, A、B、C三点在对称轴两侧,可以利用A点的对称点转化到对称轴左侧,依据开口向上和在对称轴左侧y随x的增大而减小进行比较大小;
导引:
探索新知
思路二:二次函数解析式和三个点的横坐标都是已知的,可以把点的坐标代入解析式求三个点的纵坐标,然后比较大小;
思路三:抛物线开口向上,顶点纵坐标最小,由图象的变化趋势可知抛物线上的点距离对称轴越近 (即离顶点越近)纵坐标越小,从而进行比较大小.
探索新知
方法一:∵y=(x-2)2-1,∴对称轴为直线x=2.
∴点A(4,y1)关于x=2的对称点是(0,y1).
∵-2<0< 且a=1>0,∴y2
在抛物线y=(x-2)2-1上.
∴y1=3,y2=5-4 ,y3=15.
∵5-4 <3<15,∴y2
探索新知
方法三:设点A、B、C三点到抛物线对称轴的距离分别为d1、d2、d3.
∵y=(x-2)2-1,∴对称轴为直线x=2.
∴d1=2,d2=2- ,d3=4,
∵2- <2<4,且a=1>0,
∴y2
抛物线上点的纵坐标比较大小的基本方法:
(1)把各点利用抛物线上的对称点的纵坐标相等,把各点转化
到对称轴的同侧,再利用二次函数的增减性进行比较大小;
(2)当已知具体的抛物线的解析式及相应点的横坐标确定时,
可先求出相应点的纵坐标,然后比较大小;
(3)利用“开口向上,抛物线上的点距离对称轴越近,点的纵
坐标越小,开口向下,抛物线上的点距离对称轴越近,
点的纵坐标越大”也可以比较大小.
总 结
探索新知
3
知识点
二次函数y=a(x-h)2+k与y=ax2之间的关系
思考:抛物线y=a(x-h)2+k与抛物线y=ax2有怎样的关系?
探索新知
探索新知
归 纳
一般地,抛物线y=a(x-h)2+k与y=ax2形状相同,位置不同.把抛物线y=ax2向上(下)向左(右)平移,可以得到抛物线y=a(x-h)2+k.平移的方向、距离要根据h,k的值来决定.
探索新知
例4 将抛物线y=x2向右平移2个单位,再向上平移3个单位后,
抛物线的解析式为( )
A.y=(x+2)2+3 B. y=(x-2)2+3
C.y=(x+2)2-3 D. y=(x-2)2-3
先根据二次函数图象的平移规律,对自变量和函数值作相
应的变化,写出变化后的二次函数表达式,再选出正确的项.
由二次函数图象的平移规律可知,将抛物线y=x2先向右平移
2个单位所得抛物线的表达式为:y=(x-2)2,再向上平移3
个单位后,所得函数的表达式为y=(x-2)2+3,故应选B.
B
导引:
解:
探索新知
抛物线的平移遵循“左加右减,上加下减”的原则,具体为:
(1)上下平移:抛物线y=a(x-h)2+k向上平移m(m>0)个单位,
所得抛物线的解析式为y=a(x-h)2+k+m;抛物线y=a(x-
h)2+k向下平移m(m>0)个单位,所得抛物线的解析式
为y=a(x-h)2+k-m.
(2)左右平移:抛物线y=a(x-h)2+k向左平移n(n>0)个单位,
所得抛物线的解析式为y=a(x-h+n)2+k;抛物线y=a(x-
h)2+k向右平移n(n>0)个单位,所得抛物线的解析式为
y=a(x-h-n)2+k.特别地,要注意其中的符号处理.
典题精讲
1.设抛物线C1:y=x2向右平移2个单位长度,向下平移3个单位
长度得到抛物线C2,则抛物线C2对应的函数解析式是( )
A.y=(x-2)2-3 B.y=(x+2)2-3
C.y=(x-2)2+3 D.y=(x+2)2+3
A
2.将抛物线y=x2+1先向左平移2个单位长度,再向下平移3个
单位长度,所得抛物线对应的函数解析式是( )
A.y=(x+2)2+2 B.y=(x+2)2-2
C.y=(x-2)2+2 D.y=(x-2)2-2
B
学以致用
小试牛刀
1.二次函数y=a(x-h)2+k的图象的特征:
(1)a>0,开口________,a<0,开口________;
(2)对称轴是直线________,顶点坐标为________.
向上
向下
x=h
(h,k)
2.二次函数y=a(x-h)2+k的性质:
若a>0,当x>h时,y随x的增大而______;当x
若a<0,当x>h时,y随x的增大而________;当x
增大
减小
小
k
减小
增大
大
小试牛刀
3.抛物线y=a(x-h)2+k与y=ax2形状______,位置______.把抛物
线y=ax2向上(下)或左(右)平移,可以得到抛物线y=a(x-h)2+k,
平移的方向、距离要根据________的值来决定.
相同
不同
h,k
4.抛物线 的顶点坐标是( )
A. ,-3 B. - ,-3
C. ,3 D. - ,3
B
小试牛刀
5.二次函数y=(x+2)2-1的图象大致为( )
D
6.已知二次函数y=(x-h)2+1(h为常数),在自变量x的值满足1≤x
≤3的情况下,与其对应的函数值y的最小值为5,则h的值为( )
A.1或-5 B.-1或5
C.1或-3 D.1或3
B
小试牛刀
7.如图,在△ABC中,∠C=90°,AB=10 cm,BC=8 cm,点
P从点A沿AC向点C以1 cm/s的速度运动,同时点Q从点C沿
CB向点B以2 cm/s的速度运动(点Q运动到点B停止),在运动
过程中,四边形PABQ的面积的最小值为( )
A.19 cm2 B.16 cm2
C.15 cm2 D.12 cm2
C
小试牛刀
8.把二次函数y=a(x-h)2+k的图象先向左平移2个单位长度,再
向上平移4个单位长度,得到二次函数y= (x+1)2-1的图象.
(1)试确定a,h,k的值;
a= ,h=1,k=-5.
(2)指出二次函数y=a(x-h)2+k的图象的开口方向、对称轴和顶点坐标.
图象的开口向上,对称轴为直线x=1,
顶点坐标为(1,-5).
小试牛刀
9.如图,已知抛物线y=a(x-h)2+k与x轴的一个交
点为A(3,0),与y轴的交点为B(0,3),对称轴为
直线x=1.
(1)求抛物线对应的函数解析式;
由题意可知h=1,则y=a(x-1)2+k.将点(3,0),(0,3)的坐标代入上式,得:
故抛物线对应的函数解析式为y=-(x-1)2+4.
解得
小试牛刀
(2)已知点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标.
①当MA=MB时,M(0,0);
②当AB=AM时,M(0,-3);
③当AB=BM时,M(0,3+ )或M(0,3- ).
所以点M的坐标为(0,0),(0,-3),(0,3+ )
或(0,3- ).
小试牛刀
10.某广场中心有高低不同的各种喷泉,其中一支高度为1 m的
喷水管喷出的抛物线型水柱最大高度为3 m,此时距喷水管
的水平距离为 m,求在如图所示的平面直角坐标系中抛
物线型水柱对应的函数解析式(不要
求写出自变量的取值范围).
小试牛刀
解:∵点( ,3)是抛物线的顶点,
∴可设抛物线型水柱对应的函数解析式为
y=a(x- )2+3. ∵抛物线经过点(0,1),
∴1=(0- )2 a+3,解得a=-8.
∴抛物线型水柱对应的函数解析式为:
y=-8(x- )2+3.
课堂小结
课堂小结
二次函数y=a(x-h)2+k的图象与性质:
二次函数解析式 a的 符号 开口方向 对称轴 顶点坐标 增减性 最值
y= a(x-h)2+k a>0 向上 直线x=h (h,k) 当x>h时,y随x的增大而增大;当x<h时,y随x的增大而减小 当x=时,
y最小值
=k
a<0 向下 直线x=h (h,k) 当x<h时,y随x的增大而增大;当x>h时,y随x的增大而减小 当x=时,
y最大值=k
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
