冀教版(新)七上-1.5 有理数的加法 第一课时【优质课件】
文档属性
| 名称 | 冀教版(新)七上-1.5 有理数的加法 第一课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览











文档简介
(共35张PPT)
1.5 有理数的加法
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
引入负数后,数的范围扩大了.如何在有理数范围内进行加法运算呢
新课精讲
探索新知
1
知识点
有理数的加法法则
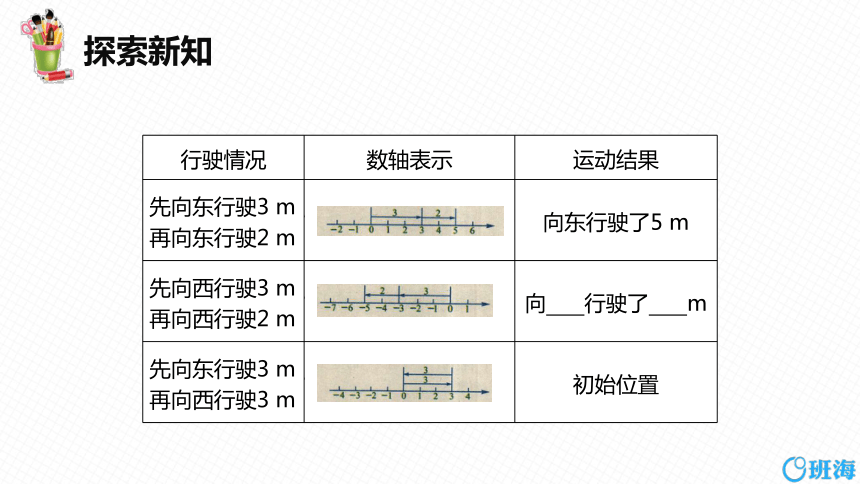
在操场上,小亮操纵遥控车模沿东西方向做定向行驶练习,每回接连行驶两次. 规定初始位置为0,向东行驶为正,向西行驶为负. 车模每回的行驶情况、数轴表示及运动结果如下表所示.
探索新知
行驶情况 数轴表示 运动结果
先向东行驶3 m, 再向东行驶2 m 向东行驶了5 m
先向西行驶3 m, 再向西行驶2 m 向 行驶了 m
先向东行驶3 m, 再向西行驶3 m 初始位置
探索新知
行驶情况 数轴表示 运动结果
先向东行驶5 m, 再向西行驶2 m 向东行驶了 3 m
先向西行驶5 m, 再向东行破2 m 向 行驶了 m
先向西行驶5 m, 然后停止不动 向西行驶了 5 m
探索新知
观察上表,完成下列问题:
(1)完成表格中的填空.
(2)请将车模每次行驶和运动结果的情况用有理数表示出来.
(3)接连两次行驶的运动结果能用算式表示吗?如果能,应怎样表示
事实上,求接连两次行驶的运动结果,用加法.按照上面对“正”“负”的规定,“向东行驶3 m,再向东行驶2 m,运动结果是向东行驶了 5 m”, 用算式表示就是
探索新知
(+3) + (+2) = +5.
(向东行驶3 m) (向东行驶2 m) (向东行驶了 5 m)
“向西行驶3 m,再向西行驶2 m,运动结果是向西行驶了 5 m”,用算式表示就是
(-3) + (-2) = -5.
(向西行驶3 m) (向西行驶2 m) (向西行驶了5 m)
类似地,另外四回运动的结果可用算式表示为:
(+3)+(-3)=0; (+5)+(-2)=+3;
(-5)+(+2)=-3;(-5)+0=-5.
探索新知
1.两个正数相加,怎样确定和的符号与和的绝对值?
2.两个负数相加,怎样确定和的符号与和的绝对值?
3.一个正数与一个负数相加,怎样确定和的符号与和的绝对值?
4.一个数同0相加,和等于什么?
探索新知
归 纳
同号两数相加,取相同的符号,并把绝对值相加. 异号两数相加,绝对值相等时和为0;绝对值不相等时,取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对值.
一个数同0相加,仍得这个数.
探索新知
计算:
(1)(+8)+(+5); (2)(+2.5)+(-2.5);
(3) (4)
例1
解:(1) (+8)+(+5)=+(8+5)=+13.
(2)(+2.5)+(-2.5)=0.
(3)
(4)
探索新知
总 结
有理数加法运算的基本方法:
一是辨别两个加数是同号还是异号,
二是确定和的符号,
三是判断应利用绝对值的和还是差进行计算.
典题精讲
计算 .
(1)(-2)+(-11); (2)(+20)+(+12); (3)
1
解:(1)(-2)+(-11)=-(2+11)=-13.
(2)(+20)+(+12)=+(20+12)=32.
(3)
典题精讲
在以下每题的横线上填写和的符号、运算过程及结果.
(1)(-15)+(-23)=______(________)=________;
(2)(-15)+(+23)=______(________)=________;
(3)(+15)+(-23)=______(________)=________;
(4)(-15)+0=________.
-
+
-
15+23
-38
23-15
8
23-15
-8
-15
3 计算(-3)+4的结果是( )
A.-7 B.-1 C.1 D.7
C
探索新知
2
知识点
有理数加法法则的一般应用
请同学们欣赏一组足球图片(如图所示),吸引“球迷们”的兴趣.
探索新知
可能很多同学喜欢足球,但同学们知道足球比赛中,对足球的规定吗?正式足球比赛对所用足球的质量有严格的规定,标准质量是400克,下面是六个足球的质量,检测结果(用正数表示超过规定质量的克数,用负数表示不足规定质量的克数):
-25,+10,-20,+30,+15,-40
这些足球的质量和是多少?
探索新知
例2 已知|a|=3,|b|=2,且a导引:要求a+b的值,必须先求出a、b的值,而a、b的值可通过已知条件求出.
解:因为|a|=3,所以a=3或a=-3.
因为|b|=2,所以b=2或b=-2.
又因为a当a=-3,b=2时,a+b=(-3)+2=-1;
当a=-3,b=-2时,a+b=(-3)+(-2)=-5.
探索新知
总 结
(1)本题先由绝对值的意义,求出a、b的值,这样a、b取值就分为了四组,再由a(2)本题的解答体现了分类讨论思想,分类时要做到不重复不遗漏.
典题精讲
若x、y互为相反数,m的绝对值为2,n是最大的负整数,求
+m+n的值.
解:因为x、y互为相反数,所以x+y=0.
又|m|=2,n是最大的负整数,所以m=±2,n=-1.
故当m=2时, +m+n=0+2+(-1)=1;
当m=-2时, +m+n=0+(-2)+(-1)=-3.
3 下面的数中,与-6的和为0的数是( )
A.6 B.-6 C. D.-
典题精讲
有理数a是最小的正整数,有理数b是最大的负整数,则a+b等于______.
0
A
探索新知
3
知识点
有理数加法的实际应用
例3 如图,海平面的高度为0 m.一艘潜艇从海平面先下潜40 m,再上升15 m.求现在这艘潜艇相对于海平面的
位置.(上升为正,下潜为负)
解:潜艇下潜40 m,记作-40 m;
上升15 m,记作+15 m.
根据题意,得(-40)+(+15)=-(40-15)=-25(m).
答:现在这艘潜艇位于海平面下 25 m 处.
探索新知
总 结
此题是具有实际意义的问题,是有理数加法的
应用题,解应用题最后必须写答,注意结果要符合
实际意义.
典题精讲
足球循环赛中,红队以4∶1战胜黄队,黄队以2∶0战胜蓝队,蓝队以1∶0战胜红队,计算各队的净胜球数.
解:规定进球记为“+”,失球记为“-”.红队的净胜球数为4+(-2)=2,黄队的净胜球数为3+(-4)=-1,蓝队的净胜球数为1+(-2)=-1.
3 A为数轴上表示-1的点,将点A沿数轴向右移动2个单位长度后到点B,则点B所表示的数为( )
A.-3 B.3 C.1 D.1或-3
典题精讲
冬天的某天早晨6点的气温是-1 ℃,到了中午气温比早晨6点时上升了8 ℃,这时的气温是____℃.
7
C
学以致用
小试牛刀
1.有理数a是最小的正整数,有理数b是最大的负整数,则a+b
等于____ .
0
2.对于两个有理数的和,下列说法正确的是( )
A.一定比任何一个有理数大
B.至少比其中一个有理数大
C.一定比任何一个有理数小
D.以上说法都不正确
D
4.两数相加,如果和小于每个加数,那么这两个加数( )
A一个为0,一个为负数
B.都是负数
C一个为正数一个为负数且负数的绝对值较大
D.符号不能确定
小试牛刀
3.两个数相加,若和为负数,则这两个数( )
A.必定都为负数 B.总是一正一负
C.可以都为正数 D.至少有一个负数
D
B
小试牛刀
5.如果a+b=0,那么a,b两个数一定( )
A.都等于0 B.一正一负
C.互为相反数 D.无法确定
6.有理数a,b在数轴上的位置如图所示,则a+b的值( )
A.大于0 B.小于0 C.小于a D.大于b
C
A
小试牛刀
7.汽车从点地出发向南行驶48千米后到达B地,又从B地向北行驶
20千米到达C地,则A地与C地的距离是( )
A. 68千米 B. 28千米
C. 48千米 D. 20千米
B
8.若()-(-2)=3,则括号内的数是( )
A.-1 B .1 C.5 D.-5
B
小试牛刀
8.小明从家里出发骑车到一个公园去玩,当他意识到骑过头的时候,已经走了4.5km,他又向回骑了1.2km才到达目的地.
(1)列算式求出小明家离公园有多远;
(2)求小明骑车行驶的路程.
解:(1)4.5一1.2=3.3(km).
答:小明家离公园3.3km.
(2)4.5+1.2=5.7(km).
答:小明骑车行驶的路程为5.7km.
课堂小结
课堂小结
有理数相加的方法口诀:
两数相加看符号,符号分为同异号;同号相加分正负,符号不变取原号,正取正号负取负号,绝对值相加错不了;异号相加大减小,符号跟着大值走.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
1.5 有理数的加法
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
引入负数后,数的范围扩大了.如何在有理数范围内进行加法运算呢
新课精讲
探索新知
1
知识点
有理数的加法法则
在操场上,小亮操纵遥控车模沿东西方向做定向行驶练习,每回接连行驶两次. 规定初始位置为0,向东行驶为正,向西行驶为负. 车模每回的行驶情况、数轴表示及运动结果如下表所示.
探索新知
行驶情况 数轴表示 运动结果
先向东行驶3 m, 再向东行驶2 m 向东行驶了5 m
先向西行驶3 m, 再向西行驶2 m 向 行驶了 m
先向东行驶3 m, 再向西行驶3 m 初始位置
探索新知
行驶情况 数轴表示 运动结果
先向东行驶5 m, 再向西行驶2 m 向东行驶了 3 m
先向西行驶5 m, 再向东行破2 m 向 行驶了 m
先向西行驶5 m, 然后停止不动 向西行驶了 5 m
探索新知
观察上表,完成下列问题:
(1)完成表格中的填空.
(2)请将车模每次行驶和运动结果的情况用有理数表示出来.
(3)接连两次行驶的运动结果能用算式表示吗?如果能,应怎样表示
事实上,求接连两次行驶的运动结果,用加法.按照上面对“正”“负”的规定,“向东行驶3 m,再向东行驶2 m,运动结果是向东行驶了 5 m”, 用算式表示就是
探索新知
(+3) + (+2) = +5.
(向东行驶3 m) (向东行驶2 m) (向东行驶了 5 m)
“向西行驶3 m,再向西行驶2 m,运动结果是向西行驶了 5 m”,用算式表示就是
(-3) + (-2) = -5.
(向西行驶3 m) (向西行驶2 m) (向西行驶了5 m)
类似地,另外四回运动的结果可用算式表示为:
(+3)+(-3)=0; (+5)+(-2)=+3;
(-5)+(+2)=-3;(-5)+0=-5.
探索新知
1.两个正数相加,怎样确定和的符号与和的绝对值?
2.两个负数相加,怎样确定和的符号与和的绝对值?
3.一个正数与一个负数相加,怎样确定和的符号与和的绝对值?
4.一个数同0相加,和等于什么?
探索新知
归 纳
同号两数相加,取相同的符号,并把绝对值相加. 异号两数相加,绝对值相等时和为0;绝对值不相等时,取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对值.
一个数同0相加,仍得这个数.
探索新知
计算:
(1)(+8)+(+5); (2)(+2.5)+(-2.5);
(3) (4)
例1
解:(1) (+8)+(+5)=+(8+5)=+13.
(2)(+2.5)+(-2.5)=0.
(3)
(4)
探索新知
总 结
有理数加法运算的基本方法:
一是辨别两个加数是同号还是异号,
二是确定和的符号,
三是判断应利用绝对值的和还是差进行计算.
典题精讲
计算 .
(1)(-2)+(-11); (2)(+20)+(+12); (3)
1
解:(1)(-2)+(-11)=-(2+11)=-13.
(2)(+20)+(+12)=+(20+12)=32.
(3)
典题精讲
在以下每题的横线上填写和的符号、运算过程及结果.
(1)(-15)+(-23)=______(________)=________;
(2)(-15)+(+23)=______(________)=________;
(3)(+15)+(-23)=______(________)=________;
(4)(-15)+0=________.
-
+
-
15+23
-38
23-15
8
23-15
-8
-15
3 计算(-3)+4的结果是( )
A.-7 B.-1 C.1 D.7
C
探索新知
2
知识点
有理数加法法则的一般应用
请同学们欣赏一组足球图片(如图所示),吸引“球迷们”的兴趣.
探索新知
可能很多同学喜欢足球,但同学们知道足球比赛中,对足球的规定吗?正式足球比赛对所用足球的质量有严格的规定,标准质量是400克,下面是六个足球的质量,检测结果(用正数表示超过规定质量的克数,用负数表示不足规定质量的克数):
-25,+10,-20,+30,+15,-40
这些足球的质量和是多少?
探索新知
例2 已知|a|=3,|b|=2,且a
解:因为|a|=3,所以a=3或a=-3.
因为|b|=2,所以b=2或b=-2.
又因为a
当a=-3,b=-2时,a+b=(-3)+(-2)=-5.
探索新知
总 结
(1)本题先由绝对值的意义,求出a、b的值,这样a、b取值就分为了四组,再由a
典题精讲
若x、y互为相反数,m的绝对值为2,n是最大的负整数,求
+m+n的值.
解:因为x、y互为相反数,所以x+y=0.
又|m|=2,n是最大的负整数,所以m=±2,n=-1.
故当m=2时, +m+n=0+2+(-1)=1;
当m=-2时, +m+n=0+(-2)+(-1)=-3.
3 下面的数中,与-6的和为0的数是( )
A.6 B.-6 C. D.-
典题精讲
有理数a是最小的正整数,有理数b是最大的负整数,则a+b等于______.
0
A
探索新知
3
知识点
有理数加法的实际应用
例3 如图,海平面的高度为0 m.一艘潜艇从海平面先下潜40 m,再上升15 m.求现在这艘潜艇相对于海平面的
位置.(上升为正,下潜为负)
解:潜艇下潜40 m,记作-40 m;
上升15 m,记作+15 m.
根据题意,得(-40)+(+15)=-(40-15)=-25(m).
答:现在这艘潜艇位于海平面下 25 m 处.
探索新知
总 结
此题是具有实际意义的问题,是有理数加法的
应用题,解应用题最后必须写答,注意结果要符合
实际意义.
典题精讲
足球循环赛中,红队以4∶1战胜黄队,黄队以2∶0战胜蓝队,蓝队以1∶0战胜红队,计算各队的净胜球数.
解:规定进球记为“+”,失球记为“-”.红队的净胜球数为4+(-2)=2,黄队的净胜球数为3+(-4)=-1,蓝队的净胜球数为1+(-2)=-1.
3 A为数轴上表示-1的点,将点A沿数轴向右移动2个单位长度后到点B,则点B所表示的数为( )
A.-3 B.3 C.1 D.1或-3
典题精讲
冬天的某天早晨6点的气温是-1 ℃,到了中午气温比早晨6点时上升了8 ℃,这时的气温是____℃.
7
C
学以致用
小试牛刀
1.有理数a是最小的正整数,有理数b是最大的负整数,则a+b
等于____ .
0
2.对于两个有理数的和,下列说法正确的是( )
A.一定比任何一个有理数大
B.至少比其中一个有理数大
C.一定比任何一个有理数小
D.以上说法都不正确
D
4.两数相加,如果和小于每个加数,那么这两个加数( )
A一个为0,一个为负数
B.都是负数
C一个为正数一个为负数且负数的绝对值较大
D.符号不能确定
小试牛刀
3.两个数相加,若和为负数,则这两个数( )
A.必定都为负数 B.总是一正一负
C.可以都为正数 D.至少有一个负数
D
B
小试牛刀
5.如果a+b=0,那么a,b两个数一定( )
A.都等于0 B.一正一负
C.互为相反数 D.无法确定
6.有理数a,b在数轴上的位置如图所示,则a+b的值( )
A.大于0 B.小于0 C.小于a D.大于b
C
A
小试牛刀
7.汽车从点地出发向南行驶48千米后到达B地,又从B地向北行驶
20千米到达C地,则A地与C地的距离是( )
A. 68千米 B. 28千米
C. 48千米 D. 20千米
B
8.若()-(-2)=3,则括号内的数是( )
A.-1 B .1 C.5 D.-5
B
小试牛刀
8.小明从家里出发骑车到一个公园去玩,当他意识到骑过头的时候,已经走了4.5km,他又向回骑了1.2km才到达目的地.
(1)列算式求出小明家离公园有多远;
(2)求小明骑车行驶的路程.
解:(1)4.5一1.2=3.3(km).
答:小明家离公园3.3km.
(2)4.5+1.2=5.7(km).
答:小明骑车行驶的路程为5.7km.
课堂小结
课堂小结
有理数相加的方法口诀:
两数相加看符号,符号分为同异号;同号相加分正负,符号不变取原号,正取正号负取负号,绝对值相加错不了;异号相加大减小,符号跟着大值走.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
