人教版(新)九上-22.2 二次函数与一元二次方程 第三课时【优质课件】
文档属性
| 名称 | 人教版(新)九上-22.2 二次函数与一元二次方程 第三课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
22.2 二次函数
与一元二次方程
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课前导入
情景导入
利用图象信息解决二次函数的问题主要是运用数形结合思想将图象信息转换为数学语言,掌握二次函数的图象和性质是解决此类问题的关键.
新课精讲
探索新知
1
类型
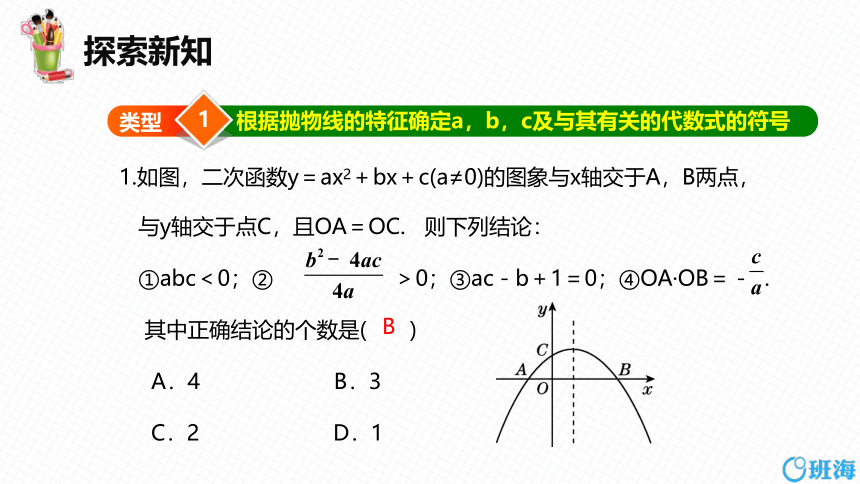
根据抛物线的特征确定a,b,c及与其有关的代数式的符号
1.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,
与y轴交于点C,且OA=OC. 则下列结论:
①abc<0;② >0;③ac-b+1=0;④OA·OB=- .
其中正确结论的个数是( )
A.4 B.3
C.2 D.1
B
探索新知
2
类型
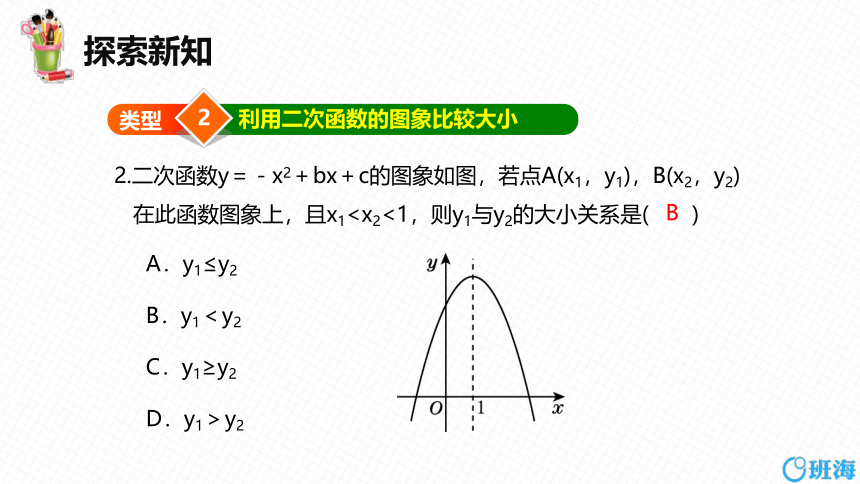
利用二次函数的图象比较大小
2.二次函数y=-x2+bx+c的图象如图,若点A(x1,y1),B(x2,y2)
在此函数图象上,且x1A.y1≤y2
B.y1<y2
C.y1≥y2
D.y1>y2
B
探索新知
3
类型
利用二次函数的图象求方程的解或不等式的解集
3.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则当函数值y>0时,
x的取值范围是( )
A.x<-1
B.x>3
C.-1<x<3
D.x<-1或x>3
D
探索新知
4
类型
根据抛物线的特征确定其他函数的图象
4.二次函数y=ax2+bx的图象如图所示,那么一次函数y=ax+b
的图象大致是( )
C
学以致用
小试牛刀
1.如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:
①a>0; ②2a+b=0;
③a+b+c>0; ④当-1<x<3时,
y>0.其中正确的个数为( )
A.1
B.2
C.3
D.4
C
小试牛刀
2.二次函数y=-x2+bx+c的图象如图,若点A(x1,y1),B(x2,y2)在
此函数图象上,且x1A.y1≤y2
B.y1<y2
C.y1≥y2
D.y1>y2
B
小试牛刀
3.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则当函数值y>0
时,x的取值范围是( )
A.x<-1
B.x>3
C.-1<x<3
D.x<-1或x>3
D
小试牛刀
4.如图,一次函数y1=kx+n与二次函数y2=ax2+bx+c的图象相交
于A(-1,5),B(9,2)两点,则关于x的不等式kx+n≥ax2+bx+c
的解集为( )
A.-1≤x≤9
B.-1≤x<9
C.-1<x≤9
D.x≤-1或x≥9
A
小试牛刀
5.如图,二次函数y=ax2+bx+3的图象经过点A(-1,0),B(3,0),
那么关于x的一元二次方程ax2+bx=0
的根是_________________.
x1=0,x2=2
6.已知函数y=(x-a)(x-b)(其中a>b)的图象如图所示,则函数
y=ax+b的图象是( )
D
小试牛刀
7.如图,A(-1,0),B(2,-3)两点在
一次函数y1=-x+m与二次函数y2
=ax2+bx-3的图象上.
(1)求m的值和二次函数的解析式;
解:将点A(-1,0)的坐标代入y+1=-x+m,得m=-1;
将点A(-1,0),B(2,-3)的坐标分别代入y2=ax2+bx-3,
得
解得
∴y2=x2-2x-3.
小试牛刀
(2)设二次函数的图象交y轴于点C,求△ABC的面积.
易知C点的坐标为(0,-3),
又∵B点的坐标为(2,-3),
∴BC∥x轴.
∴S△ABC= ×(2-0)×[0-(-3)]
= ×2×3=3.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
22.2 二次函数
与一元二次方程
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课前导入
情景导入
利用图象信息解决二次函数的问题主要是运用数形结合思想将图象信息转换为数学语言,掌握二次函数的图象和性质是解决此类问题的关键.
新课精讲
探索新知
1
类型
根据抛物线的特征确定a,b,c及与其有关的代数式的符号
1.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,
与y轴交于点C,且OA=OC. 则下列结论:
①abc<0;② >0;③ac-b+1=0;④OA·OB=- .
其中正确结论的个数是( )
A.4 B.3
C.2 D.1
B
探索新知
2
类型
利用二次函数的图象比较大小
2.二次函数y=-x2+bx+c的图象如图,若点A(x1,y1),B(x2,y2)
在此函数图象上,且x1
B.y1<y2
C.y1≥y2
D.y1>y2
B
探索新知
3
类型
利用二次函数的图象求方程的解或不等式的解集
3.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则当函数值y>0时,
x的取值范围是( )
A.x<-1
B.x>3
C.-1<x<3
D.x<-1或x>3
D
探索新知
4
类型
根据抛物线的特征确定其他函数的图象
4.二次函数y=ax2+bx的图象如图所示,那么一次函数y=ax+b
的图象大致是( )
C
学以致用
小试牛刀
1.如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:
①a>0; ②2a+b=0;
③a+b+c>0; ④当-1<x<3时,
y>0.其中正确的个数为( )
A.1
B.2
C.3
D.4
C
小试牛刀
2.二次函数y=-x2+bx+c的图象如图,若点A(x1,y1),B(x2,y2)在
此函数图象上,且x1
B.y1<y2
C.y1≥y2
D.y1>y2
B
小试牛刀
3.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则当函数值y>0
时,x的取值范围是( )
A.x<-1
B.x>3
C.-1<x<3
D.x<-1或x>3
D
小试牛刀
4.如图,一次函数y1=kx+n与二次函数y2=ax2+bx+c的图象相交
于A(-1,5),B(9,2)两点,则关于x的不等式kx+n≥ax2+bx+c
的解集为( )
A.-1≤x≤9
B.-1≤x<9
C.-1<x≤9
D.x≤-1或x≥9
A
小试牛刀
5.如图,二次函数y=ax2+bx+3的图象经过点A(-1,0),B(3,0),
那么关于x的一元二次方程ax2+bx=0
的根是_________________.
x1=0,x2=2
6.已知函数y=(x-a)(x-b)(其中a>b)的图象如图所示,则函数
y=ax+b的图象是( )
D
小试牛刀
7.如图,A(-1,0),B(2,-3)两点在
一次函数y1=-x+m与二次函数y2
=ax2+bx-3的图象上.
(1)求m的值和二次函数的解析式;
解:将点A(-1,0)的坐标代入y+1=-x+m,得m=-1;
将点A(-1,0),B(2,-3)的坐标分别代入y2=ax2+bx-3,
得
解得
∴y2=x2-2x-3.
小试牛刀
(2)设二次函数的图象交y轴于点C,求△ABC的面积.
易知C点的坐标为(0,-3),
又∵B点的坐标为(2,-3),
∴BC∥x轴.
∴S△ABC= ×(2-0)×[0-(-3)]
= ×2×3=3.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
